Edge-Vertex Dominating Sets and Edge-Vertex Domination Polynomials of Cycles

A. Vijayan¹, J. Sherin Beula^2*

¹Department of Mathematics, Nesamony Memorial Christian College, Marthandam, India.
²Department of Mathematics, Mar Ephraem College of Engineering & Technology, Marthandam, India.

DOI: 10.4236/ojdm.2015.54007                

Abstract

Let G = (V, E) be a simple graph. A set S E(G) is an edge-vertex dominating set of G (or simply an ev-dominating set), if for all vertices v V(G); there exists an edge eS such that e dominates v. Let denote the family of all ev-dominating sets of with cardinality i. Let . In this paper, we obtain a recursive formula for . Using this recursive formula, we construct the polynomial, , which we call edge-vertex domination polynomial of (or simply an ev-domination polynomial of ) and obtain some properties of this polynomial.

Keywords

ev-Domination Set, ev-Domination Number, ev-Domination Polynomials

1. Introduction

Let G = (V, E) be a simple graph of order |V| = n. A set S Í V(G) is a dominating set of G, if every vertex 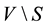is adjacent to at least one vertex in S. For any vertex v Î V, the open neighbourhood of n is the set 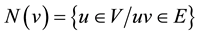and the closed neighbourhood of n is the set. For a set S Í V, the open neighbourhood of S is 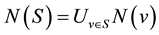and the closed neighbourhood of S is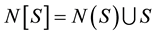. The domination number of a graph G is defined as the minimum size of a dominating set in G and it is denoted as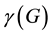. A cycle is defined as a closed path, and is denoted by.

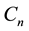Definition 1.1

For a graph G = (V, E), an edge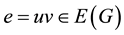, ev-dominates a vertex if

1) u = w or v = w (w is incident to e) or

2) uw or vw is an edge in G (w is adjacent to u or v).

Definition 1.2 [1]

A set is an edge-vertex dominating set of G (or simply an ev-dominating set), if for all vertices; there exists an edge such that e dominates v. The ev-domination number of a graph G is defined as the minimum size of an ev-dominating set of edges in G and it is denoted as.

Definition 1.3

Let be the family of ev-dominating sets of a graph with cardinality i and let . We call the polynomial the ev-domination polynomial of the graph.

In the next section, we construct the families of the ev-dominating sets of cycles by recursive method. As usual we use for the largest integer less than or equal to x and for the smallest integer greater than or equal to x. Also, we denote the set by [e_n] and the set by [n], throughout this paper.

2. Edge-Vertex Dominating Sets of Cycles

Let be the family of ev-dominating sets of with cardinality i. We investigate the ev-domina- ting sets of. We need the following lemma to prove our main results in this section.

Lemma 2.1: [2] .

By Lemma 2.1 and the definition of ev-domination number, one has the following Lemma:

Lemma 2.2: if and only if or.

Lemma 2.3: If a graph G contains a simple path of length 4k − 1, then every ev-dominating set of G must contain at least k vertices of the path.

Proof: The path has 4k vertices. As every edge dominates at most 4 vertices, the 4k vertices are covered by at least k edges.

Lemma 2.4. If, and there exists x Î [e_n] such that then .

Proof: Suppose that. Since, Y contains at least one edge labelled e_n−5, e_n−6 or e_n−7.

If, then, a contradiction. Hence or, but then in this case for any x Î [e_n], also a contradiction.

Lemma 2.5. [3]

1) If then.

2) If, and then and.

3) If, , , and, then.

Proof: 1) Since, by Lemma 2.2, or. In either case, we have and.

2) Since and, by Lemma 2.2, we have and. Hence and. Therefore, and.

3) By hypothesis, or. Therefore, or. Therefore, or. Therefore,.

Lemma 2.6. [4] If, then

1) and if and only if n = 4k and i = k for some k Î N.

2) and if and only if i = n.

3), , , , if and only if n = 4k + 2 and for some k Î N.

4), , and if and only if i = n ? 2.

5), , and if and only if i = n ? 1.

6), , and if and only if.

Proof: 1) (Þ) Since, by Lemma 2.2, or. If, then and by Lemma 2.2, , a contradiction.

So

(2.1)

and since, we have

(2.2)

From (2.1) and (2.2),

(2.3)

When n is a multiple of 4, and. Therefore,. Therefore, , we get. Thus, when, (2.3) holds good and. When, and. Therefore, , which is not possible.

Hence and

(Ü) If n = 4k and i = k for some k Î N, then by Lemma 2.2,. Therefore, , which implies. Similarly, and.

Now. Therefore, , which implies.

2) (Þ) Since, by Lemma 2.2, or. If then by Lemma 2.2, , a contradiction.

So

(2.4)

Since,

, (2.5)

From (2.4) and (2.5), we have. Therefore,. Therefore,

(Ü) If, then by Lemma 2.2,. Therefore,

Therefore,

3) (Þ) Since, by Lemma 2.2, or. If, then, by Lemma 2.2, a contradiction.

Therefore, , which implies,

(2.6)

Since, ,.

Hence,

(2.7)

Similarly,

(2.8)

and

(2.9)

From (2.6), (2.7), (2.8) and (2.9),

(2.10)

Therefore, (2.10) hold when or and, for some. Suppose, then and. Therefore, from (2.10), we have, , which implies. Suppose, i.e.,.

Case 1) When.

From (2.10), we get and. Therefore, , which is not possible.

Case 2) When. From (2.10), we get and. Therefore, , which is not possible.

Case 3) When. From (2.10), we get and

Therefore, , which is not possible. Therefore,

(Ü) If n = 4k + 2 and for some k Î N, and, then by Lemma 2.2, ,. Therefore,. Therefore,.

Also,. Therefore, and and.

Hence, ,.

4) (Þ) Since, by Lemma 2.2,

or (2.11)

Since, by Lemma 2.2,

(2.12)

Similarly, and, by Lemma 2.2

(2.13)

and

(2.14)

From (2.11), we get which is not possible.

Therefore,

(2.15)

From (2.12),

(2.16)

From (2.15) and (2.16),

(Ü) If, then by Lemma 2.2, or. Therefore,. Also, therefore,;, therefore,; and, therefore,.

5) (Þ) Since by Lemma 2.2,

or (2.17)

Since by Lemma 2.2,

or (2.18)

Since and, by Lemma 2.2,

(2.19)

and

(2.20)

From (2.19) and (2.20), we have. From (2.18), we have. Therefore,. But. Therefore,. Therefore,.

(Ü) If, then by Lemma 2.2, and therefore, and, therefore, and, therefore,.

6) (Þ) Since, , , and, by Lemma 2.2, , , , and. So and hence.

(Ü) If, then by Lemma 2.2 we have, , , ,.

Therefore, , , , and.

Theorem 2.7 [5]

For every and,

1) If and then .

2) If and then .

3) If and then , where

4) If, , and then

5) If then

Proof:

1) Since, and, by Lemma 2.6 (i), and for some. The sets have elements and each one covers all vertices. Also, no other sets of cardinality covers all vertices. Therefore, the collection of ev-dominating sets of cardinality is

Hence,.

2) We have and. By Lemma 2.6 (2), we have i = n. So,.

3) We have and, by Lemma 2.6 (3), and, for some.

Let

We shall prove that. It is clear that, , and. Therefore,.

Conversely, Let. Suppose, Y is of the form, then. Now suppose, and Y is of the form then. Now suppose, , and. We split as four parts. If with then and and. If with then and and. If with then and and. If with then and and. In this case Y is of the form then. Therefore, . Thus, we have proved that

where

.

4) If, by Lemma 3.6 (iv).

Therefore.

5)

Clearly,

Conversely, let. Then. If, then we can write, for some. If and then we can write, for some. If and then we can write, for some. If, , then we can write, for some.

Therefore we proved that

Hence,

3. Edge-Vertex Domination Polynomials of Cycles

Let be the ev-domination polynomial of a cycle. In this section, we derive the expression for.

Theorem 3.1 [6]

1) If is the family of ev-dominating sets with cardinality i of, then

where.

2) For every,

with the initial values

,

,

,

.

Proof:

1) Using (1), (2), (3), (4) and (5) of Theorem 2.7, we prove (1) part.

Suppose, and then, .

Therefore,. In this case and . Therefore, in this case the theorem holds.

Suppose, and, then Therefore,. In this case. Therefore, and. Therefore, in this case the theorem holds.

Suppose,. In this case,

where

Therefore,. Also, and . Therefore, and . Therefore, in this case the theorem holds.

Suppose,

Then we have.

Therefore,. In this case, , and . Therefore,

.

Therefore, in this case the theorem holds.

Suppose,. In this case, we have

Therefore,

Hence,

.

with the initial values

We obtain for 1 ≤ n ≤ 16 as shown in Table 1.

In the following Theorem, we obtain some properties of.

Theorem 3.2

The following properties hold for the coefficients of;

1), for every n Î N.

2), for every n Î N.

3), for every n ³ 2.

4), for every n ³ 3.

5), for every n ³ 4.

6), for every n ³ 5.

7), for every n Î N.

Proof:

1) Since, we have.

2) Since, we have the result for every n Î N.

3) Since, we have for n ³ 2.

4) By induction on n. The result is true for. (from Table 1). Therefore, the result is true for n = 3. Now suppose that the result is true for all numbers less than ‘n’ and we prove it for n. By Theorem 3.1

Table 1., the number of ev-dominating set of with cardinality i.

5) By induction on n, the result is true for. (from Table 1). . Therefore, the result is true for. Now suppose the result is true for all natural numbers less than n. By Theorem 3.1,

6) By induction on n, the result is true for n = 5. (from Table 1)

Therefore the result is true for.

Now suppose that the result is true for all natural numbers less than n and we prove it for n. By Theorem 3.1,

7) From the table it is true.

Theorem 3.3

1)

2) For every,

3) If, then for every n ≥ 5, with initial values, , , and.

Proof:

1) We prove by induction on n.

First suppose that n = 2 then,

We have the result.

2) By Theorem 3.1, we have

Therefore, we have the result.

3) By Theorem 3.1, we have

4. Concluding Remarks

In [7] , the domination polynomial of cycle was studied and obtained the very important property, . It is interesting that we have derived an analogues relation for the edge-vertex domination of cycles of the form,

. One can characterise the roots of the polynomial and identify whether they are real or complex. Another interesting character to be investigated is whether is log-concave or not.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Sampath Kumar, E. and Kamath, S.S. (1992) Mixed Domination in Graphs. Sankhya: The Indian Journal of Statistics, 54, 399-402.
[2]	Alikhani, S. and Peng, Y.-H. (2009) Dominating Sets and Domination Polynomials of Paths. International Journal of Mathematics and Mathematical Sciences, 2009, Article ID: 542040. http://dx.doi.org/10.1155/2009/542040
[3]	Alikhani, S. and Peng, Y.-H. (2009) Dominating Sets and Domination Polynomials of Cycles.
[4]	Vijayan, A. and Sherin Beula, J. (2014) ev-Dominating Sets and ev-Domination Polynomials of Paths. International Organization of Scientific Research Journal of Mathematics, 10, 7-17.
[5]	Vijayan, A. and Lal Gipson, K. (2013) Dominating Sets and Domination Polynomials of Square of Paths. Open Journal of Discrete Mathematics, 3, 60-69.
[6]	Chartand, G. and Zhang, P. (2005) Introduction to Graph Theory. McGraw-Hill, Boston.
[7]	Alikhani, S. and Peng, Y.-H. (2009) Introduction to Domination Polynomial of a Graph.