Further Discussion on the Calculation of Fourier Series

Caixia Zhang

College of Mathematics and Statistics, Northeast Petroleum University, Daqing, China.

DOI: 10.4236/am.2015.63054                

Abstract

Fourier series is an important mathematical concept. It is well known that we need too much computation to expand the function into Fourier series. The existing literature only pointed that its Fourier series is sine series when the function is an odd function and its Fourier series is cosine series when the function is an even function. And on this basis, in this paper, according to the function which satisfies different conditions, we give the different forms of Fourier series and the specific calculation formula of Fourier coefficients, so as to avoid unnecessary calculation. In addition, if a function is defined on [0,a], we can make it have some kind of nature by using the extension method as needed. So we can get the corresponding form of Fourier series.

Keywords

Fourier Coefficients, Fouries Series, Period, Series Expansion, Extension

1. Preliminary Knowledge

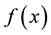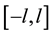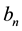Definition 1 [1] -[3] Let be an integrable function on. Then the coefficients and are calculated by

and are called the Fourier coefficients of.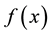

Definition 2 [1] -[5] Let 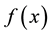with the period 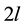be an integrable function on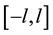, trigonometric series with the Fourier coefficient are called Fourier series of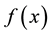, denoted by

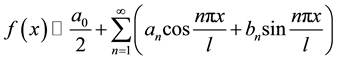
Lemma 1 [6] Let 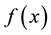be an integrable function on 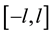with period of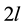, the Fourier coefficients are calculated according to period of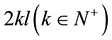. The calculation indicates there are same results between Fourier

series with period of and.

2. Calculating Fourier Series According to the Nature of the Function

Theorem 1 Let be an integrable function on and satisfy the condition, then we have

where, ,.

Proof It was clear that the period of is and we have

Let, then. Therefore

.

So we get

.

.

Let, then. Therefore

Therefore, we obtain

In the same way, we have

In a word, while is an even number, , and

Thus in this case, the expansion reduces to

Theorem 2 Let be an integrable function on and satisfy the conditions, then we have

where,.

Proof The period of is, so we can calculate Fouries series of with period of by Lemma 1. We have

Let, then. Therefore

So we get

Let, then. Therefore

We obtain

In the same way, we have

Thus in this case, the expansion reduces to

where,.

Theorem 3 Let be an integrable function on. When, it satisfies the condition. Then we have

(1) While is an even function in, then we get

where.

(2) While is an odd function in，then we get

where.

Proof (1) We use the method of periodic extension to with period of.

Because is an even function, we have,.

Let, , then we have

Let, therefore

We obtain

Thus in this case, the expansion reduces to

where.

(2) In the same way, we can prove Theorem 3 (2).

Similarly, we can prove the following Theorem 4.

Theorem 4 Let be an integrable function on. When, it satisfies the condition. Then we have

(1) While is an even function in, then we get

where.

(2) While is an odd function in, then we get

where.

3. Conclusion

Suppose the function is defined on, if we use symmetry extension about the point and then

use odd and periodic extension, we can get two forms of Fourier series as Theorem 3. If we use symmetry ex-

tension about the line and then use odd and periodic extension, we can get two forms of Fourier series as Theorem 4. Suppose the function is defined on, we have a similar conclusion.

Acknowledgements

I would like to thank the referees and the editor for their valuable suggestions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Department of Mathematics of East China Normal University (2010) Mathematical Analysis. 4th Edition, Higher Education Press, Beijing, 62-72. (In Chinese)
[2]	He, G.Z. (2008) Discussion on a Style of Fourier Series Expansion. Journal of Leshan Teachers College, 23, 27-28. (In Chinese)
[3]	Zheng, C. and Qiu, W.G. (2010) Integration Techniques Based on Fourier. Studies in College Mathematics, 13, 31-32. (In Chinese)
[4]	Wang, B.Y. and Qi, X.S. (2011) Two Methods for Summing Trigonometric Series. Studies in College Mathematics, 14, 33-34. (In Chinese)
[5]	Jiao, H.Y. and Liu, W.H. (2011) Fourier Expansion and a Class of Series. Studies in College Mathematics, 14, 35-36. (In Chinese)
[6]	Ding, X.H. (2004) Several Problems of Fouries Series Expansion. Journal of Daxian Teachers College (Natural Sci ence Edition), 14, 1-4. (In Chinese)