On the FOM Algorithm for the Resolution of the Linear Systems Ax = b

Mongi Benhamadou

Department of Mathematics, Faculty of Sciences of Sfax, Sfax, Tunisia.

DOI: 10.4236/alamt.2014.43014                

Abstract

In this paper, we propose another version of the full orthogonalization method (FOM) for the resolution of linear system Ax = b, based on an extended definition of Sturm sequence in the calculation of the determinant of an upper hessenberg matrix in o(n²). We will also give a new version of Givens method based on using a tensor product and matrix addition. This version can be used in parallel calculation.

Keywords

FOM, Krylov Subspace, Hessenberg Matrix, Sturm Sequence, Givens Method

1. Introduction

The resolution of linear systems 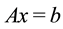is in the heart of numerous scientific applications: discretization of partiel differentiel equations, image processing, the linearization of nonlinear problems in a sequence of linear problems [1] [2] [3] etc. There are many kinds of methods that resolve linear systems. Some are direct, others are iterative. Generally, direct methods [4] - [6] , such as Gauss, Cholesky, QR, are efficient and proved solvers of small size systems. But for problems of big size, these methods require quite prohibitive memory space and therefore become numerically expensive. More and more, they are replaced by iterative methods. Most iterative methods [2] [6] [7] treat linear systems through vector-matrix products with an appropriate data structure permitting the exploitation of sparsity of the matrix 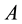by storing only nonzero elements which are indi- spensable for the calculation of these products, which reduces both the memory size and the processing time. We distinguish two kinds of iterative methods for the resolution of linear systems:

The asymptotic methods [6] - [8] are older and simpler to implement. Among the most known ones, we mention Jacobi ’s, Gauss-Seidel’s and the relaxation methods. Generally, these methods remain less reliable than the direct methods, and more or less efficient with some specific problems. Currently, these methods are no longer used as linear solvers but remain interesting as preconditioners for other iterative methods. The increase of the size of the systems to be solved leads to the projection methods.

Krylov methods: They are being used for some time and proved to be very efficient [2] . Their analysis is more complicated than that of the asymptotic methods. They are based on a technique of projection on a Krylov

subspace, having the form:;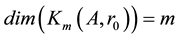, spanned by the succe-

ssive powers of applied to the risudual vector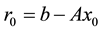, where 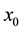is a vector of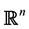, these Krylov’s subspaces constitute an increasing sequence of subspaces, one being included in the other and permitting the construction of a sequence of vectors converging towards the solution. The convergence of these methods is theorically assured for maximum. The Krylov methods resolve linear systems having nonsymmetric matrices. The most used Krylov methods based on Arnoldi algorithm are: the full orthogonalization method (FOM) and its varieties: the method of minimal residue (or shortly GMRES), Lanczos method, and that of conjugate gradient for symmetric and symmetric positive definite matrices. These projection methods are more generalisable, more powerful and currently the most used.

In the first section, we will review the orthogonal projection methods on Krylov’s subspaces, focusing on the FOM method for the resolution of linear systems.

In the second section, we will extend the definition of Sturm sequence, which will serve for the calculation of the determinant of upper hessenberg matrices.

In the third section, we will give a new variety of Givens method [4] for the resolution of linear systems having an upper hessenberg matrix.

Finally, in the fourth section, we report the results of some numerical tests.

In what follows, we consider a real regular square matrix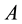, a vector and the correspondent linear system:

(1)

If 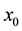is a starting approximation of solution (1), then the residual vector associated to is. We call Krylov space of order, noted, the vectorial space spanned by and its iterated by:

(2)

1.1. The Projection Method

In this part, we will review generallities over iterative methods of projection for the resolution of linear systems (1), by using projections in particular subspaces, namely Krylov’s spaces [1] [2] .

Most actual iterative techniques used in solving large linear systems use in one way or another a projection procedure. The main idea of projection techniques consist in extracting an approximate solution to system (1) of a subspace of. It leads to a small linear system. This is a basic projection step. If we take of dimension (the subspace searched for), then, generally, constraints must be imposed in order to be able to extract such an approximation. One usual way of describing these constraints is to impose to the residual vectors to be orthogonal to the linearly independent vectors, this will define another subspace noted with dimension, which we call “constraints space”. We are then seeking an approximate solution to problem (1) by imposing that and that the new residual vector must be orthogonal to. If, in addition, we want to use the starting approximation, then the approximate solution must be searched for in the affine space, then the solution of (1) will be characterized as follows:

(3)

As such, the definition of the projection method is based on two conditions:

The first fixes the “place” where we should look for the solution at the iteration: usually, this place is an affine subvariety of. According to Krylov’s methods, this affine subvariety is, which gives us the following “space condition”:

(4)

The second condition must fix the that is appropriate to that space (4). We hope that minimizes the vector error, or the residual vector or one or those two vectors be orthogonal to a space of dimension. This condition is called “Petrov-Galerkin condition”, and is expressed as follows:

(5)

As for the projection method, we will study in the next part, Arnoldi’s method for the resolution of linear systems. Let’s start now by recalling Arnoldi’s algorithm.

1.2. Arnoldi’s Algorithm

Arnoldi’s Algorithm is an iterative process consisting in calculating, simultaneously, an orthonormal basis of, and an upper hessenberg matrix. The matrix is a representation of with respect to this basis.

In practice, constructing Krylov’s spaces leads to determining basis. The natural basis

can never be used, due to its numerical degeneration, and the Krylov’s matrices become increasingly ill-condi- tioned [2] . To avoid this numerical degeneration of the natural basis of Krylov’s space, the solution consists in putting in place an orthonormalization process. Arnoldi’s basis is then constructed by applying the modified Gram-Schmidt orthonormalization method to vectors obtained by successive products matrix vector for euclidien inner product. The Arnoldi’s algorithm takes the following form:

If we assign as coefficient of orthogonalization of with respect to, and as norm of vector obtained by orthogonalization of vector with respect to vectors, then, the formula of Arnoldi’s basis construction can be written:

(6)

Let be the matrix having rows and columns, in which the columns are the first vectors of the Arnoldi’s basis. The orthonormality of vectors, in terms of matrices can be written:

(7)

Likewise, Equation (6), which defines Arnoldi’s vectors, can be translated matricially by:

(8)

where the matrix is a matrix having rows and columns where coefficients are the coefficients of orthonormalization of the Equation (6): where for, and the other coefficients being zero.

(9)

The main diagonal block of is a square matrix of dimension, noted, which, according the Equations (7) and (8), verifies:

(10)

Such a matrix is called “upper hessenberg”:.

Equation (10) shows that is the matrix of the projection in Krylov’s space of the linear map associated to the matrix A, in the basis of Arnoldi’s vectors. This can be summed up as follows:

Proposition 1:

In Arnoldi’s algorithm, we have at the step the following relations:

(11)

where is the vector of the canonical basis of

Proof: [2] .

1.3. Arnoldi’s Method for Linear Systems (FOM)

In this paragraph, we will remind the important results needed for the resolution of linear systems (1).

For that, we will begin by applying the Arnoldi’s algorithm to the matrix, this allows us to obtain at each step, a matricial pair where is an orthonormal basis of Krylov’s space, and

is specific an upper hessenberg matrix given by (9).

The full orthogonalization method (FOM) is variant of problem (3), verifying the space condition (4) and “Petrov-Galerkin condition” (5) by taking. This method is defined by:

(12)

Production of the Solution

We are seeking the solution verifying the space condition (4) and “Petrov-Galerkin condition” (5).

(4) with.

So, the residual vector is written:

(13)

and “Petrov-Galerkin condition” becomes:

(5), with (13)

but then

. This is equivalent to:

(14)

So, (14) implies, and the solution can be written:

(15)

and the problem becomes:

A method based on this approach is called a full orthogonalization method (FOM). It is given by Y. Saad in 1981.

This is the corresponding algorithm using the Arnoldi’s process.

The algorithm depends on parameter, which is the dimension of the Krylov’s subspace. In practice, it is desirable to select in a dynamic way. This is possible if the norm of the residue of the solution is calculated with a numerically low cost. (without having to compute itself). Then the algorithm can be stopped at the appropriate step using this information. The following result gives an answer in this direction.

Proposition 2:

The residue vector of the approximate solution calculated by the algorithm is such that:

and so,

(16)

Proof: [2] .

At this stage, the interesting feature is the possibility to compute the norm of residue without producing the solution.

According to this proposition, at the step, the residual norm is then given directly by the absolute value of the last component of the vector. This provides the stopping test and

allows to calculate only when the stopping criterion used for the solution is satisfied. This is the main idea of this article. It consists in calculating locally, at each iteration, uniquely the last component of the

vector: solution of the system (14). The classical formulae of Cramer’s rule directly gives the component in the form of a determinant quotient:, the computation of determi-

nants is given by the following result:

Proposition 3:

Let be an invertible upper hessenberg matrix and, the second member of the linear system (14). Then we have:

(17)

with:

(18)

(19)

What we need now, is to calculate; being an upper hessenberg matrix.

2. Sturm Sequence for the Upper Hessenberg Matrices (U.H)

In this paragraph, we extend the definition of Sturm sequence to the hessenberg matrices, and then we give an algorithm computing their determinants. Let’s start by reminding the following principal result:

Proposition 4:

Let be an (U.H) matrix and let be the principal submatrix of, i.e.,

and let be the charcteristic polynomial of, then: the polynomial, are given by to the following recurrent formula :

(20)

Proof: by recurrence.

Definition 1:

The sequence defined by (20) is called Sturm sequence of the upper hessenberg matrix.

Remark 1:

We note that, for the programming, we can win memory words if we use a storage numbering

function [8] for upper hessenberg matrices by storing nonzero elements uniquely.

2.1. Computing the Determinant of the Hessenberg Matrix

For calculating the determinant of an upper hessenberg matrix, Proposition (2) gives us a simple method in. This can be summed by the following result:

Corollary 1:

Let be an invertible (U.H) matrix. If we set, then we have:

(21)

. In the Formula (21), we calculate the products, without repeting multiplications. So, we obtain a very interesting algorithm computing as follows:

The number of operations necessary in calculating is:

additions:

multiplications:.

The total number of operations required is. This is more convenient when is big.

We will adopt the algorithm in the full orthogonalization method (FOM). Having at each step,

, we calculate by the Formulaes (18) and (19):. This gives us the stopping test and

allows to calculate only when the stopping criterion used for the solution is satisffied, namely:

where, being the required precision. The FOM algorithm takes the following form:

When the stopping criterion used for the solution is satisffied, we take the value for calculating

by using the following algorithm:

2.2. Algorithm of Resolution of the System:

The above algorithm requires flops.

Several authors solve the linear system using Givens method applied to an upper hessenberg matrix.

3. The Givens Method for (U.H) Matrices

In this section, we give a new variant of the Givens method for the resolution of linear systems with an upper hessenberg matrices coming from Arnoldi’s algorithm. This method is based on the addition of two matrices and two tensorial products.

The Givens rotations constitute an important tool to selectively eliminate certain coefficients of a matrix. This is the case of our upper hessenberg matrix, where we eliminate the codiagonal in order to obtain an upper triangular matrix.

To justify the next results, we introduce the following notations:

: the row of the matrix at the step.

: the matrix with the and row put to zero.

: column vector of.

: the superscript will denote the matrix or the transposed vector.

: tensor product of two vectors in.

: column vector of the rotation matrix in the plan.

3.1. Givens Formulation for Upper Hessenberg Matrices

The classical formulation of the Givens method for an upper hessenberg matrix is given under the following form:

(22)

with is of the form:

(23)

with and where and are calculated at each step by the following formulas:

(24)

The relations (22) give us an upper triangular matrix,:

(25)

and therefore

As the matrices are orthogonal, we have:, from which

(26)

Theorem 1:

If is an invertible upper hessenberg matrix, then

(27)

where is the row vector of the matrx and is the column vector of the matrix.

The Givens algorithm for the triangularisation of the matrix (U.H), is simplified to be written in its new form:

3.1.1 . Complexity of the Algorithm

To eliminate the (n − 1) elements situated under the diagonal, we need (n − 1) rotations. Each rotation requires 5 operations and an extraction of a square root.

For a fixed k

® Computation of tensor product:

:

:

® Computation of matricial addition:

:

and, we have:

Conclusion: The complexity of Givens’ algorithm for an upper hessenberg matrix requires flops and.

In consequense, we find the calculating formula of the determinant of the matrix given by:

Corollary 2 :

Let be an (U.H) matrix. By applying classical Givens’ formulation, given by the relation (22) and the Formula (26), we obtain:

(28)

We can decompose matrix (U.H) of rank, into an addition of a triangular matrix and matrices of rang 1 given by:

(29)

3.1.2 . Numerical Example

Let be an invertible matrix (U.H), and.

We want to resolve.

We apply the algorithm to the augmented matrix by the second member.

step k = 1

Compute the rotation in plane:

Column 1:; column 2:

step k = 2

Compute the rotation in plane:

Column 2:; column 3:

step k = 3

Compute the rotation in plane:

Column 3:; column 4:

we obtain a triangular system whose solution is:

and we have.

4. Numerical Tests

In this section, we present four numerical tests for the resolution of linear systems (1): for the pro- posed new version of full orthogonalization method (FOM). These tests are done using a portable DELL (Latitude D505 intel (R) Pentium (R) M, processor 1.70 GHz, 594 MHz) and a program written in, with double precision.

Test 1: is band (SPD) matrix, , [9] and is the exact solution.

From test 1, we deduce the following numerical results in Table 1.

Test 2: is a full matrix, is the exact solution, and is the inverse matrix.

where: which imply:.

(30)

From test 2, we deduce the following numerical results in Table 2.

Test 3:

In the third test, we focus our attention on the resolution of the partial differential equations with Neuman condition:

(31)

with:

Table 1. Test 1’ s numerical results.

Table 2. Test 2’ s numerical results.

If we consider as a solution, we obtain the function:

(32)

as a second member.

After doing a regular maillage and numbering the nodes, the calculation of the stiffness matrix leads to a (SPD) “well-conditioned” matrix. For the resolution we use the new version of full orthogonalization method (FOM).

Table 3 contains the numerical results of Test 3:

Test 4: is band, (SPD) matrix, , [9] .

(33)

On the one hand, the numerical results for the matrices are considerably polluted with rounding errors because the matrices are very “ill-conditioned” But on the other hand, we are constructing matrices very “well-conditioned” from matrices with translations:

where.

From Test 4, we deduce the following numerical results in Table 4.

Table 3. Test 3’ s numerical results.

Table 4. Test 4’ s numerical results.

5. Conclusions

Test 1 and 2 show the results of applying the proposed new version of full orthogonalization method (FOM): the dimension of Krylov’s space is acceptable compared to because the matrices are moderately “ill-conditioned”.

For the third test, the stiffness matrix coming from the discretization of the partial differential Equations (31) leads to a (SPD) well-conditioned matrix. We note that dimension of Krylov’s space is weak com- pared to, which can give a positive judgment about the new version of (FOM) method.

In the final test, the constructed matrices are very “well-conditioned”, and the dimension is as small as required.

Acknowledgements

The author is grateful to the referees for their valuable comments and suggestions which have helped to improve the presentation of this work.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Toumi, A. (2005) Utilisation des filtres de Tchebycheff et construction de préconditionneurs spéciaux pour l’accélération des methods de Krylov. Thèse No. 2296, de l’Institut National Polytechnique de Toulouse, France.
[2]	Saad, Y. (2000) Iterative Methods for Sparse Linear Systems. 2nd Edition, Society for Industrial and Applied Mathematics, Philadelphia.
[3]	Benhamadou, M. (2000) Développement d’outils en Programmation Linéaire et Analyse Numérique matricielle. Thèse No. 1955, de l’Université Paul Sabatier Toulouse 3, Toulouse, France.
[4]	Wilkinson, J.H. (1965) The Algebraic Eigenvalue Problem. Clarendon Press, Oxford.
[5]	Gastinel, N. (1966) Analyse Numérique Linéaire. Hermann, Paris.
[6]	Ciarlet, P.G. (1980) Introduction à l’Analyse Numérique Matricielle et à l’Optimisation. Masson, Paris.
[7]	Lascaux, P. and Théodor, R. (1993) Analyse Numérique Matricielle Appliquée à l’Art de l’Ingénieur. Tome 1, Tome 2, Masson, Paris.
[8]	Jennings, A. (1980) Matrix Computation for Engineers and Scientists. John Wiley and Sons, Chichester.
[9]	Gregory, R.T. and Karney, D.L. (1969) A Collection of Matrices for Testing Computational Algorithms. Wiley-Inter-science, John Wiley & Sons, New York, London , Sydney, Toronto.