One-Sample Bayesian Predictive Analyses for an Exponential Non-Homogeneous Poisson Process in Software Reliability ()
1. Introduction
Over the last decade of the 20th century and the first few years of the 21st century, the demand for complex software systems has gone high as it is seen that today, computers are embedded in automotive mechanical and safety control systems, industrial and quality process control, real-time sensor networks, aircrafts, nuclear reactors, hospital healthcare and air traffic control systems among others; computer systems have become an indispensable component of our modern society today. Consequently, the reliability of software used in these systems has been a major concern and a requirement in the modern generation. Software reliability is defined as the probability of failure-free software operations for a specified period of time in a specified environment [1] . A single software defect can cause system failure and to avoid these failures, reliable software is required. Software reliability is achieved through testing during the software development testing stage [2] . The usual criteria of removing bugs in software are by running test cases in a manner that exercises the software similar to the way that users will operate in their particular environment. However, emulating end-user environment during the test interval is difficult and time-consuming especially when there are multiple types of end-users and also, business pressure to release a software system within a tight market window puts a constraint on the amount of time that can be spent testing the software. Software reliability modeling comes in handy to address this dilemma. As indicated by [3] , software reliability modeling can provide the basis for planning reliability growth tests, monitoring progress and estimating current reliability and forecasting and predicting future reliability improvements. Forecasting and prediction are achieved through predictive analyses. In particular, predictive analyses are useful in determining when to terminate the development process of software or hardware. Often, a prediction interval is constructed to provide the time frame when the 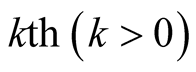 future failure observation will occur with a pre-determined confidence level [4] .
future failure observation will occur with a pre-determined confidence level [4] .
Many software reliability models have been developed by various authors and researchers in the past three decades. Amongst, an Exponential Nonhomogeneous Poisson Process with intensity function
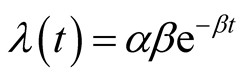 (1)
(1)
is the earliest software reliability model to be developed by Goel and Okumoto in 1979. In various literatures, this NHPP is called the Goel-Okumoto (1979) model.
As noted by [5] , the Goel-Okumoto (1979) model has been applied to a number of software testing environments and its application on assessing and detecting software failures has been investigated by various authors. For instance, the Goel-Okumoto model has been used to develop a statistical control mechanism that could be used to detect whether a software process is statistically under control or not. ML estimation of the parameters of the Goel-Okumoto (1979) model has been conducted and in particular, it has been shown that the ML estimates of the parameters of the model are not consistent as the testing period extends to infinity. [6] presented an empirical method for selecting software reliability growth models for release decision-making where they applied iteratively various software reliability models namely Goel-Okumoto (1979), Delayed S-shaped, Gompertz and Yamada exponential software reliability growth models to weekly cumulative software failure data during system test to determine the number of remaining failures expected in software after release. [7] also performed parameter estimation of the Goel-Okumoto, Yamada S-shaped and Inflection S-shaped software reliability growth models where they also established a necessary and sufficient condition with respect to the software failure data, of which, if satisfied, will ensure that the MLE method returns a unique positive and finite estimation of the unknown parameters of the Goel-Okumoto and the Yamada S-shaped models. [8] presented software failure data which, after study, depicted that the failure rate, i.e. the number of failures per hour, seemed to be decreasing with time, an indication that a Nonhomogeneous Poisson Process with mean value function 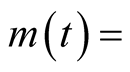
 , a mean value function corresponding to that of the Goel-Okumoto software reliability model, was a reasonable model to describe the failure process. From the literature, it is evident that most of the study that has been done on the Goel-Okumoto software reliability model is parameter estimation using, especially, the MLE method and model fit. There is a conspicuous absence of literature on both the classical and Bayesian predictive analyses on the model.
, a mean value function corresponding to that of the Goel-Okumoto software reliability model, was a reasonable model to describe the failure process. From the literature, it is evident that most of the study that has been done on the Goel-Okumoto software reliability model is parameter estimation using, especially, the MLE method and model fit. There is a conspicuous absence of literature on both the classical and Bayesian predictive analyses on the model.
This paper focuses on single-sample predictive inference for the Goel-Okumoto (1979) software reliability model using Bayesian approach. We first identify four issues in the single-sample prediction associated closely with the development testing process of software and proceed to develop and derive the corresponding predictive distributions in Section 2. The main results for single-sample prediction are presented in Section 3. A real example in the form of secondary software failure data in the form of execution times between successive software failures is used to illustrate the proposed and developed methodologies in Section 4. A discussion is given in Section 5 and thereafter, mathematical proofs are given in the Appendix.
2. Predictive Issues and Bayesian Method
During the development testing stage of a software, statisticians and engineers are overly interested in various predictive problems whose solutions are believed to be very important in modifying, debugging and determining when to terminate software development testing process. In this section, we present four issues associated closely with software development testing process and derive the predictive distributions using Bayesian approach. For the purposes of the four predictive issues, we assume that a reliability growth testing is performed on a software and the cumulative number of failures of the software in the time interval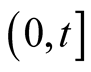 , denoted by
, denoted by 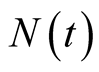 is observed. We further assume that
is observed. We further assume that 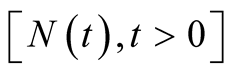 follows the NHPP with intensity function given in Equation (1). Let
follows the NHPP with intensity function given in Equation (1). Let 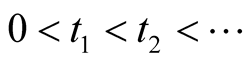 be the observed failure times. Failure data is said to be failure-truncated when testing stops after a predetermined n number of failures occur. We denote the n failure times by
be the observed failure times. Failure data is said to be failure-truncated when testing stops after a predetermined n number of failures occur. We denote the n failure times by 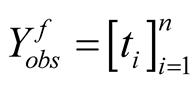 where
where . Failure data is said to be time truncated if testing stops at a predetermined time t. We denote the corresponding observed failure data by
. Failure data is said to be time truncated if testing stops at a predetermined time t. We denote the corresponding observed failure data by , where
, where .
.
Prediction interval is a confidence interval for a future observation or a function of some future observations. Specifically, a double-sided (bilateral) prediction interval for 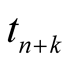 with confidence level
with confidence level 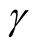 is defined by
is defined by  such that
such that . Similarly, a single-sided (unilateral) lower or upper prediction limit for
. Similarly, a single-sided (unilateral) lower or upper prediction limit for 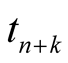 with level
with level 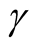 is defined by
is defined by  (or
(or ) which satisfies
) which satisfies  (or
(or ). Both
). Both  and
and 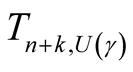 depends only on a single sample (or a single software) and are called single-sample prediction limits. Prediction limits involving two samples (or two softwares) can be defined similarly and are called two-sample prediction limits.
depends only on a single sample (or a single software) and are called single-sample prediction limits. Prediction limits involving two samples (or two softwares) can be defined similarly and are called two-sample prediction limits.
2.1. Issues in Single-Sample Software Reliability Prediction
Here, we consider one software and assume that its cumulative inter-failure times obey the Goel-Okumoto (1979) software reliability model with observed data being either 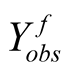 or
or . Based on
. Based on 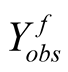 or
or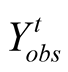 , we are interested in the following problems:
, we are interested in the following problems:
Issue A: what is the probability that at most k software failures will occur in the future time period  with
with ?
?
Issue B: suppose that the pre-determined target value 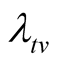 for the failure rate of the software undergoing development testing is not achieved at time T, what is the probability that the target value
for the failure rate of the software undergoing development testing is not achieved at time T, what is the probability that the target value  will be achieved at time
will be achieved at time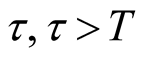 ?
?
Issue C: suppose that the target value 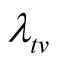 for the software failure rate is not achieved at time T, how long will it take so that the software failure rate will be attained at
for the software failure rate is not achieved at time T, how long will it take so that the software failure rate will be attained at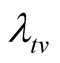 ?
?
Issue D: what is the upper prediction limit (UPL) of  with level
with level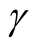 ,
, 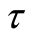 being a predetermined value greater than T?
being a predetermined value greater than T?
2.2. Posterior and Predictive Distributions
Let  represent
represent 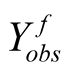 or
or . The joint density of
. The joint density of 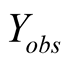 is therefore
is therefore
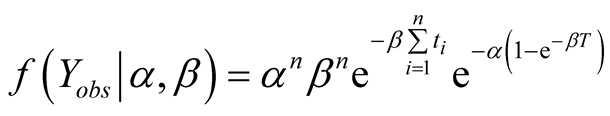 (2)
(2)
Case 1: When the shape parameter 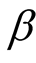 is known, we adopt the following non-informative prior distribution of
is known, we adopt the following non-informative prior distribution of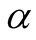 :
:
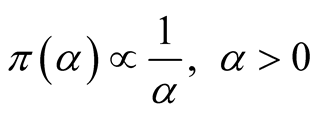 . (3)
. (3)
The posterior distribution of  is thus given by
is thus given by
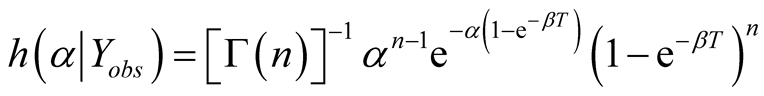 (4)
(4)
Let  be the random variable being predicted. Then the posterior predictive distribution of
be the random variable being predicted. Then the posterior predictive distribution of  is give as
is give as
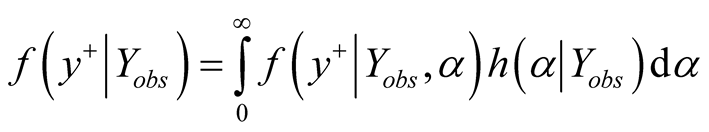 (5)
(5)
Hence the Bayesian UPL of  with level
with level 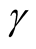 denoted as
denoted as  must satisfy
must satisfy
 . (6)
. (6)
Case 2: When the shape parameter 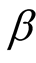 is unknown, we consider the following non-informative joint prior density for
is unknown, we consider the following non-informative joint prior density for 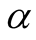 and
and 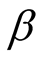 (we assume that
(we assume that 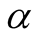 and
and 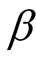 are independent).
are independent).
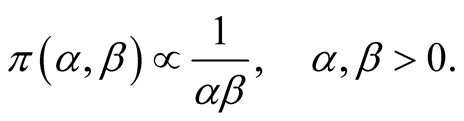 (7)
(7)
Hence the corresponding joint posterior density is given as
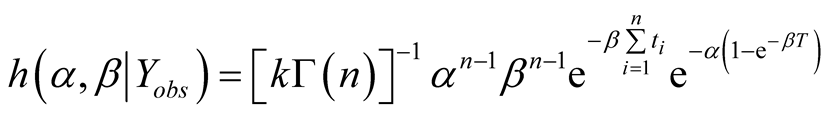 (8)
(8)
where
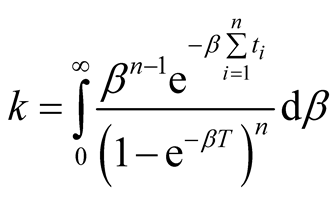 . (9)
. (9)
Similar to Equation (5) and Equation (6), let  denote the Bayesian UPL of
denote the Bayesian UPL of  with level
with level , then
, then
 (10)
(10)
and
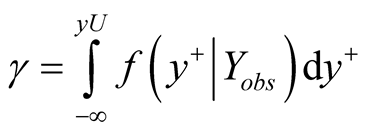 (11)
(11)
3. Main Results for the Prediction Problems
In this section, we address the four single-sample prediction issues raised in Section 2.1 using Bayesian approach. The following propositions are considered as the main results with proofs being given in the Appendix. In the subsequent results, we use  to represent the
to represent the 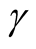 percentage point of the chi-square distribution with n degrees of freedom and we also assume the priors to be Equation (3) and Equation (7).
percentage point of the chi-square distribution with n degrees of freedom and we also assume the priors to be Equation (3) and Equation (7).
Proposition 1 (for issue A): The probability that at most k software failures will occur in the future time period 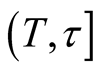 with
with 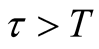 is
is
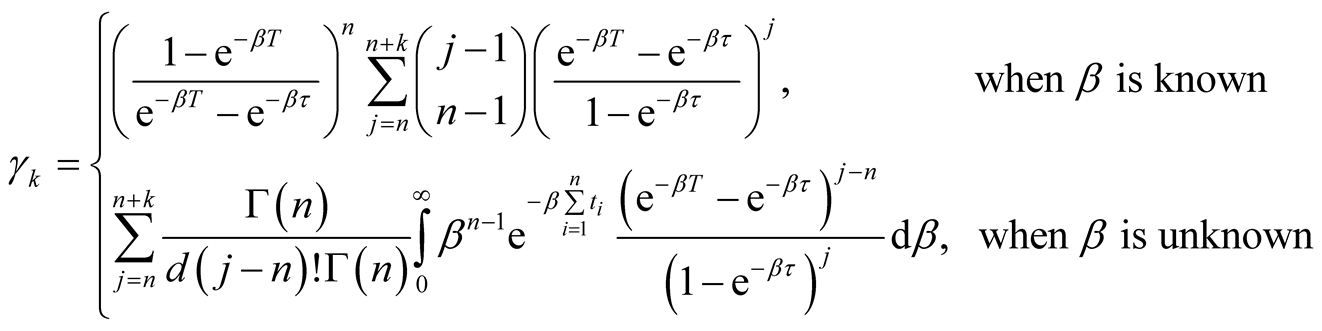 (12)
(12)
Proposition 2 (for issue B): Suppose that the pre-determined target value  for the failure rate of the software undergoing development testing is not achieved at time T, the probability that the target value
for the failure rate of the software undergoing development testing is not achieved at time T, the probability that the target value  will be achieved at time
will be achieved at time 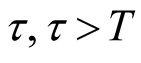 is
is
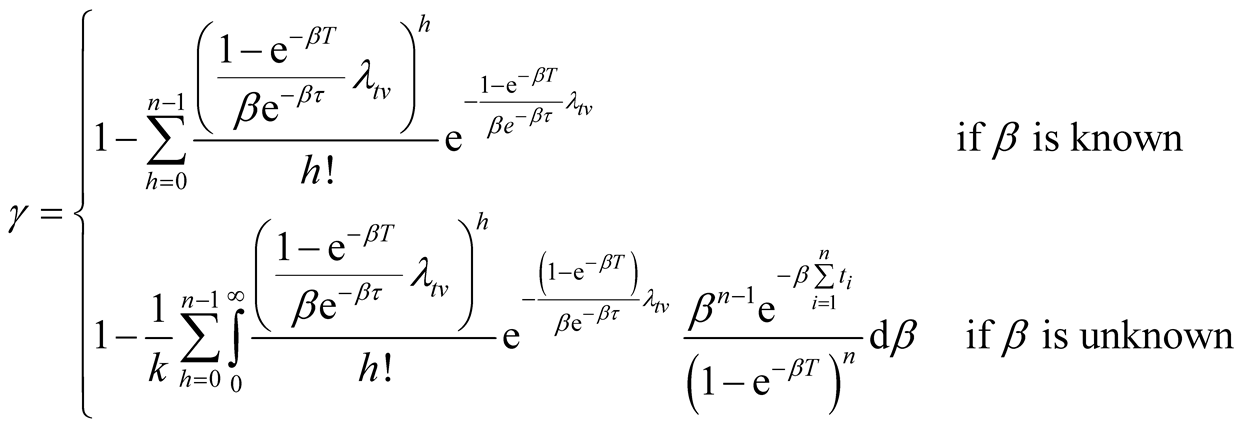 (13)
(13)
Remark 1: Let  be i.i.d. sample from
be i.i.d. sample from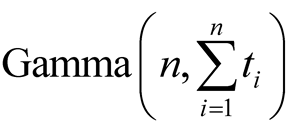 , we can approximate the second part of (13) via MCMC method.
, we can approximate the second part of (13) via MCMC method.
Proposition 3 (for issue C): For given level , the time
, the time 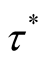 required to attain
required to attain  is
is
(i) (14)
(14)
(ii)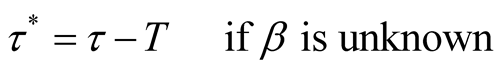 (15)
(15)
where  is the solution to the following equation:
is the solution to the following equation:
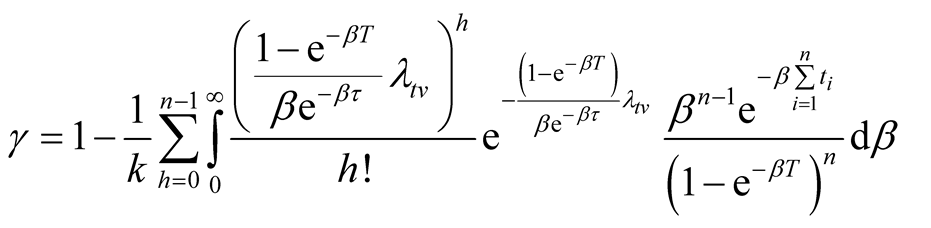 (16)
(16)
Proposition 4 (for issue D): The Bayesian UPL of  with level
with level  is
is
(i)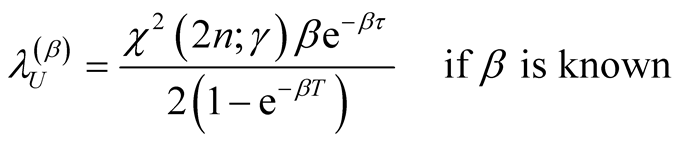 (17)
(17)
(ii) (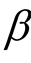 unknown)
unknown) 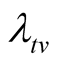 such that (18)
such that (18)
 (19)
(19)
4. Example
In this section, a real example from the time between failure data given by [9] is used to illustrate the developed methodologies for the single-sample Bayesian predictive analysis. The Table 1 gives the Time Between Failure.
The study has used the cumulative time between failures as failure times  where
where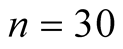 . These data obey the Goel-Okumoto (1979) software reliability model [10] . The MLEs of the parameters of the software reliability model based on the data are
. These data obey the Goel-Okumoto (1979) software reliability model [10] . The MLEs of the parameters of the software reliability model based on the data are  and
and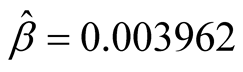 . In the illustration of the developed methodologies, the study has used these MLEs.
. In the illustration of the developed methodologies, the study has used these MLEs.
1) Suppose that we are interested in the probability  that at most k failures will occur in the future time period
that at most k failures will occur in the future time period  a) When
a) When 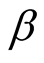 is known (say
is known (say ), using the first formula in Equation (12), we have
), using the first formula in Equation (12), we have ,
, 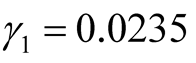 ,
,  ,
,  ,
, 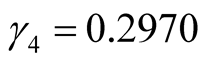 ,
, 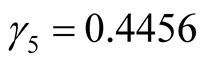 ,
,  ,
, 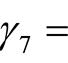 0.7193,
0.7193,  ,
,  ,
, 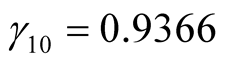 ,
,  ,
, 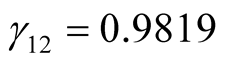 ,
, 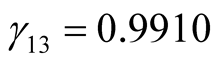 ,
,  and
and  b) When
b) When  is unknown, from the second formula in Equation (12) we obtain,
is unknown, from the second formula in Equation (12) we obtain, 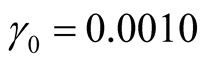 ,
,  ,
, 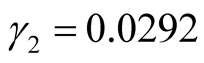 ,
,  ,
, 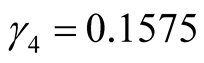 ,
,  ,
,  ,
, 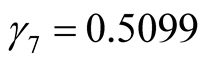 ,
,  ,
, 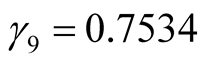 ,
,  ,
, 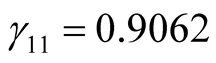 ,
, 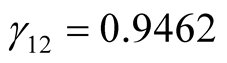 ,
, 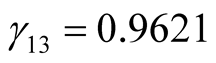 ,
, 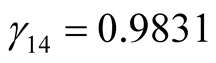 ,
,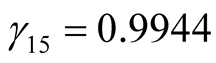 .
.
Figure 1 shows the graph of the desired probabilities for the case when 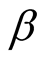 is known and when
is known and when  is unknown.
is unknown.
2) Suppose that the target value is given by . At time
. At time , the MLE of the achieved failure rate for this software is
, the MLE of the achieved failure rate for this software is  which is greater than
which is greater than  i.e. it cannot be achieved at time
i.e. it cannot be achieved at time . Thus the development testing will continue. Suppose we want to predict the probability that the target value
. Thus the development testing will continue. Suppose we want to predict the probability that the target value 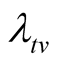 will be achieved at time
will be achieved at time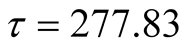 . a) When
. a) When  is known, say
is known, say , from the first formula in Equation (13) we obtain
, from the first formula in Equation (13) we obtain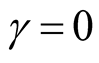 . Thus we can conclude that the target value (failure rate) will not be achieved. b) When
. Thus we can conclude that the target value (failure rate) will not be achieved. b) When 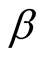 is unknown, from the second formula in Equation (13) and Remark 1, we obtain
is unknown, from the second formula in Equation (13) and Remark 1, we obtain 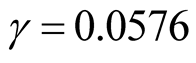 where the Monte Carlo sample size is
where the Monte Carlo sample size is .
.

Table 1. Time between failures data.
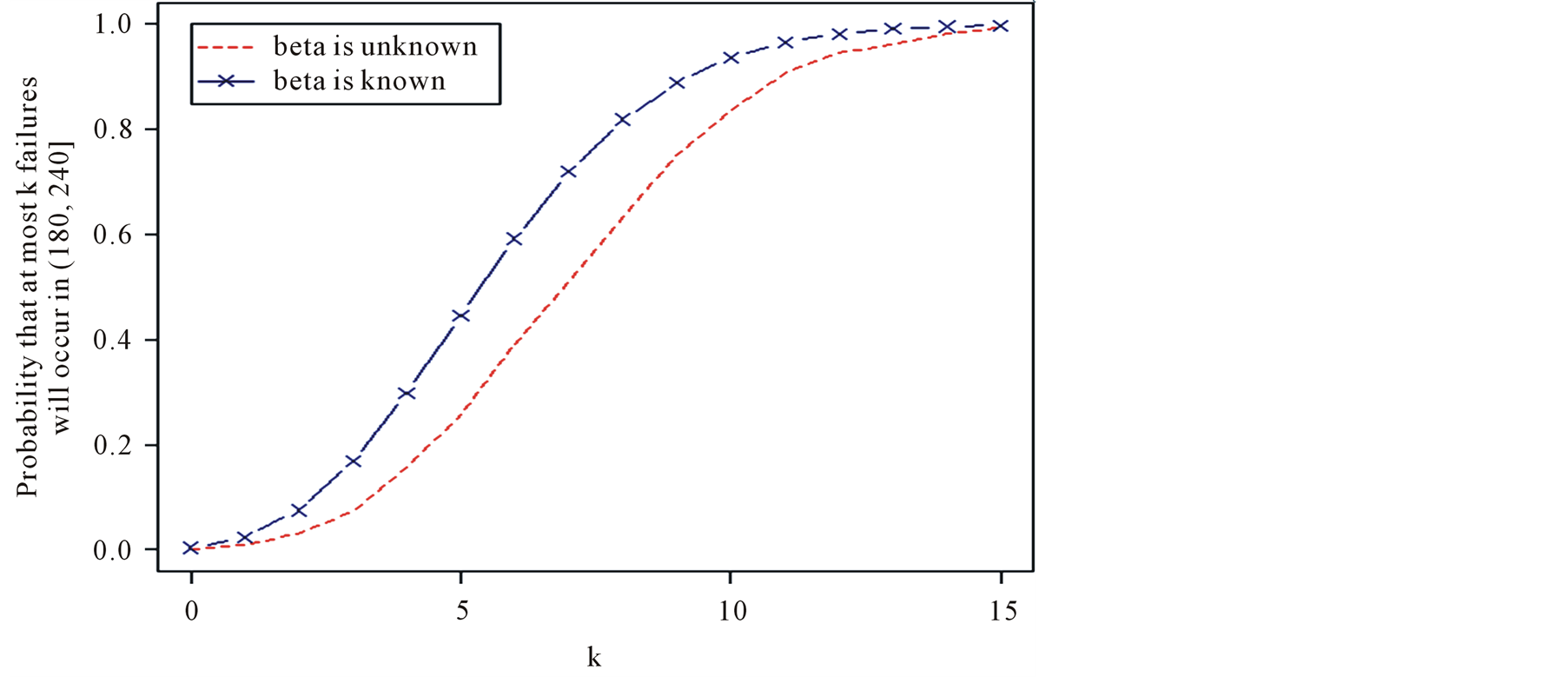
Figure 1. Comparison of the probabilities γk that at most k failures will occur in the time interval (180, 240] for the cases of known and unknown β.
3) Since the target value  was not achieved at time
was not achieved at time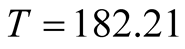 , we want to know how long it will require in order to attain
, we want to know how long it will require in order to attain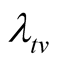 . a) When
. a) When 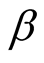 is known (i.e.
is known (i.e.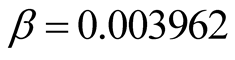 ), let
), let , from Equation (14) we obtain
, from Equation (14) we obtain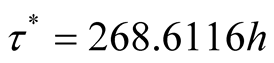 . In other words, it will take another 268.6116h in order to achieve the desired failure rate. b) When
. In other words, it will take another 268.6116h in order to achieve the desired failure rate. b) When 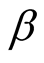 is unknown, from Equation (15) and Equation (16), we obtain
is unknown, from Equation (15) and Equation (16), we obtain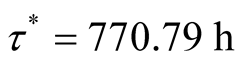 . In other words, it will take another 770.79 h in order to achieve the desired failure rate when
. In other words, it will take another 770.79 h in order to achieve the desired failure rate when 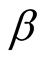 is unknown.
is unknown.
4) Given , a) when
, a) when  is known, from Equation (17), the Bayesian Upper Prediction Limit of
is known, from Equation (17), the Bayesian Upper Prediction Limit of  with level 0.90 is given by
with level 0.90 is given by  b) When
b) When 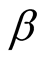 is unknown, from Equation (18) and Equation (19), the Bayesian UPL of
is unknown, from Equation (18) and Equation (19), the Bayesian UPL of 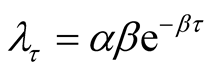 with level 0.90 is given by
with level 0.90 is given by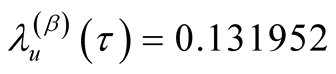 .
.
5. Discussion
Several prediction problems arise during the development of any software especially when the Goel-Okumoto (1979) software reliability model is used to model the failure process. We have used Bayesian approach with non-informative priors to address some of the prediction problems that may arise during software development testing stage. We have obtained explicit solutions to these problems, which may prove useful for the modification, debugging and for the decision to terminate the development testing process of the software.
The adoption of Bayesian approach for the derivation of the solutions is advantageous in that the approach is available for cases of small sample sizes [11] [12] . Another advantage of the Bayesian approach is that it allows the input of prior information about the reliability growth process and provides full posterior and predictive distributions.
In this paper, we have used non-informative priors to derive the methodologies to address the said prediction problems. However, informative priors can similarly be used in place of non-informative priors. The same procedures presented in this paper can also be applied to other NHPPs such as the delayed S-shaped process and the Cox-Lewis process.
Appendix (Proofs of Propositions 1 - 4)
In order to prove the propositions, we first give an identity without proof. The identity is
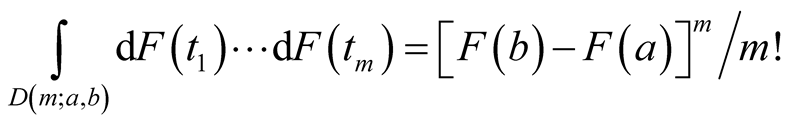 (A.1)
(A.1)
where m is any positive integer, a and b are two real numbers ,
,  is an increasing and differentiable function, and
is an increasing and differentiable function, and 
Proof of Proposition 1: The probability that at most k failures will occur in the interval 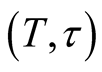 is
is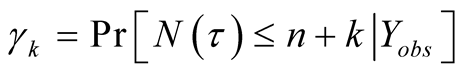 . When
. When  is known, we have
is known, we have
 (A.2)
(A.2)
where  is given by Equation (4) and
is given by Equation (4) and
 (A.3)
(A.3)
From Equation (2) we have 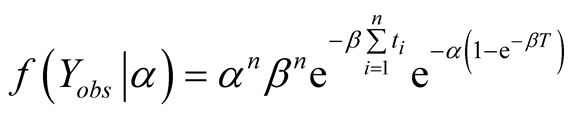 and
and

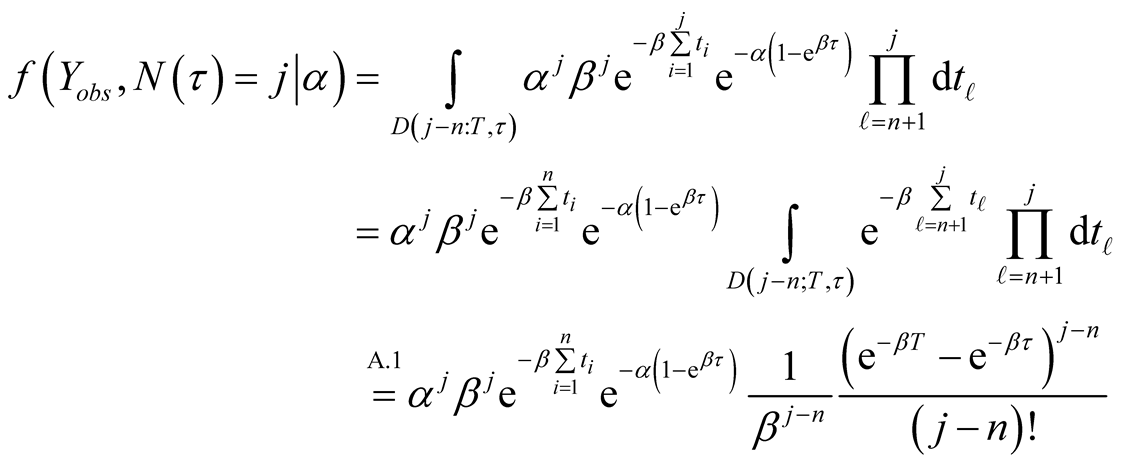 (A.4)
(A.4)
Hence (A.3) becomes
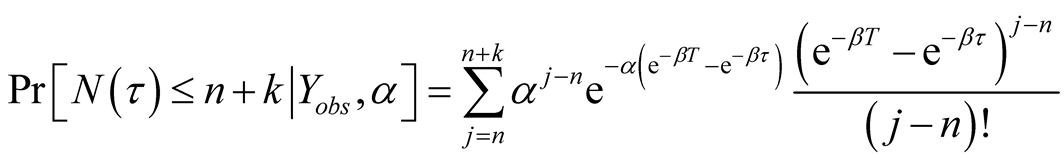 (A.5)
(A.5)
And (A.2) becomes
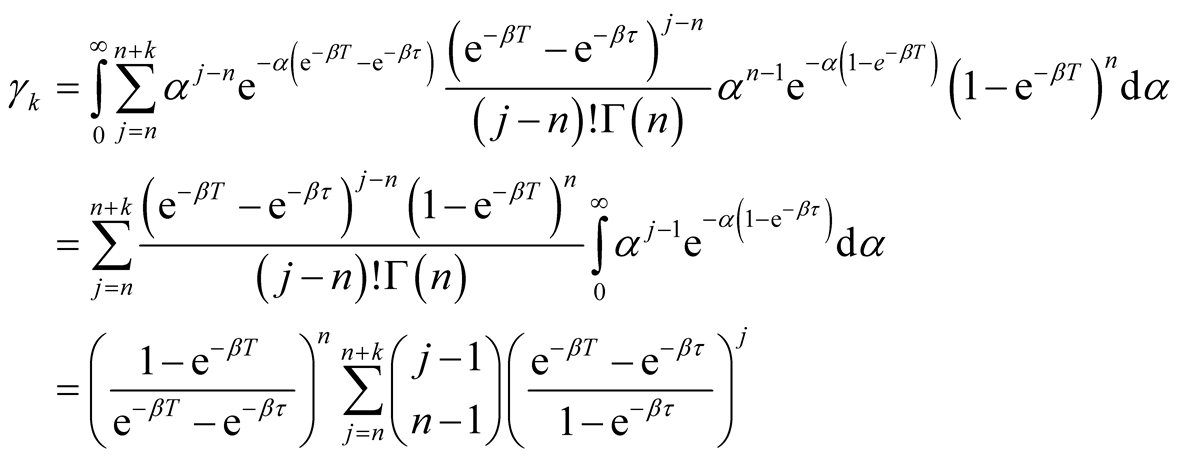 (A.6)
(A.6)
Equation (A.6) implies the first formula of Equation (12).
When 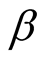 is unknown, noting that
is unknown, noting that  and
and 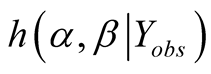 are given by Equation (A.3) and Equation (8) respectively, we have
are given by Equation (A.3) and Equation (8) respectively, we have
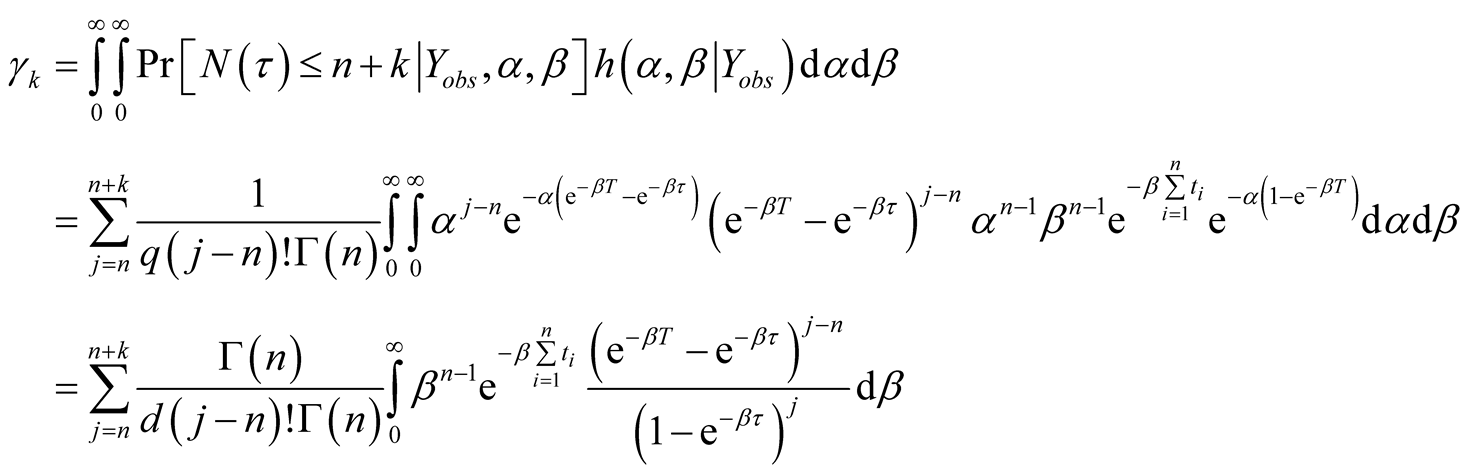 (A.7)
(A.7)
Equation (A.7) implies the second formula of Equation (12).
Proof of Proposition 2: Let  denote the posterior density of
denote the posterior density of . Hence the probability that the target value
. Hence the probability that the target value 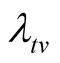 will be achieved at time
will be achieved at time 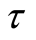
 is given by
is given by
 . (A.8)
. (A.8)
When 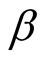 is known, making the transformation
is known, making the transformation  , we have
, we have 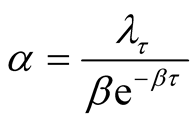 and
and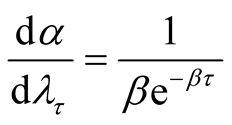 . Consequently, the posterior density of
. Consequently, the posterior density of 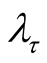 is
is . This implies that
. This implies that 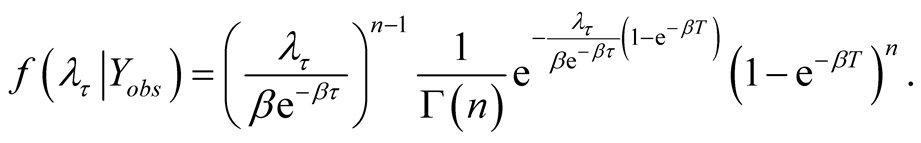
 which after simplification reduces to
which after simplification reduces to
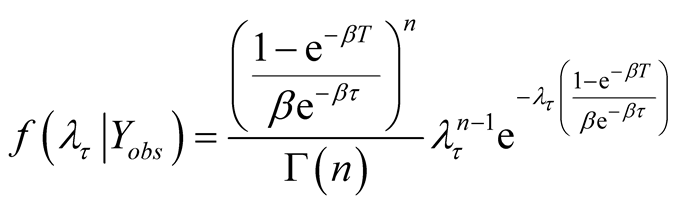 (A.9)
(A.9)
We note that  from Equation (A.9) follows a gamma distribution with parameters n and
from Equation (A.9) follows a gamma distribution with parameters n and  Noting the relationship between gamma and Poisson distributions as
Noting the relationship between gamma and Poisson distributions as
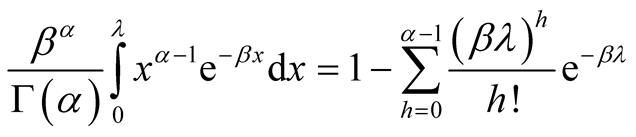 (A.10)
(A.10)
and from Equations (A.8), (A.9) and (A.10), we obtain the first formula of Equation (13).
When  is unknown, making the transformation
is unknown, making the transformation  and
and , we obtain
, we obtain 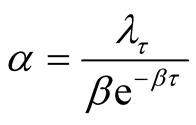 and
and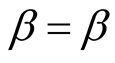 . Note that the Jacobian is
. Note that the Jacobian is 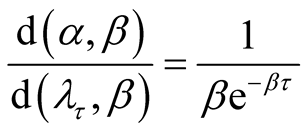 . From Equation (8), the joint posterior density of
. From Equation (8), the joint posterior density of 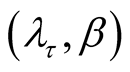 is given as
is given as
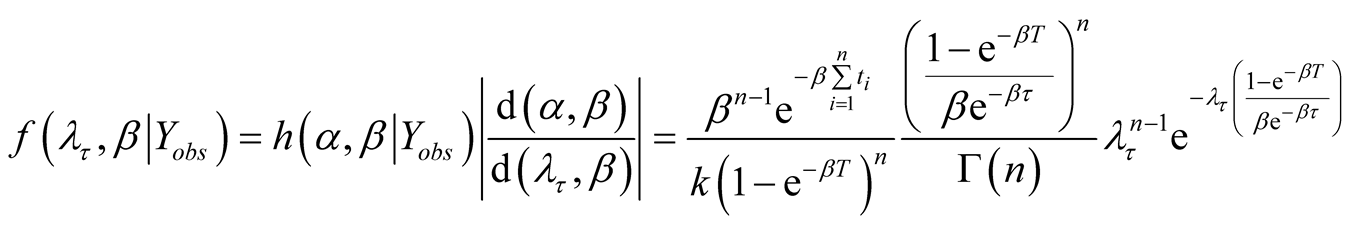 (A.11)
(A.11)
From Equation (A.8), Equation (A.10) and Equation (A.11) we obtain
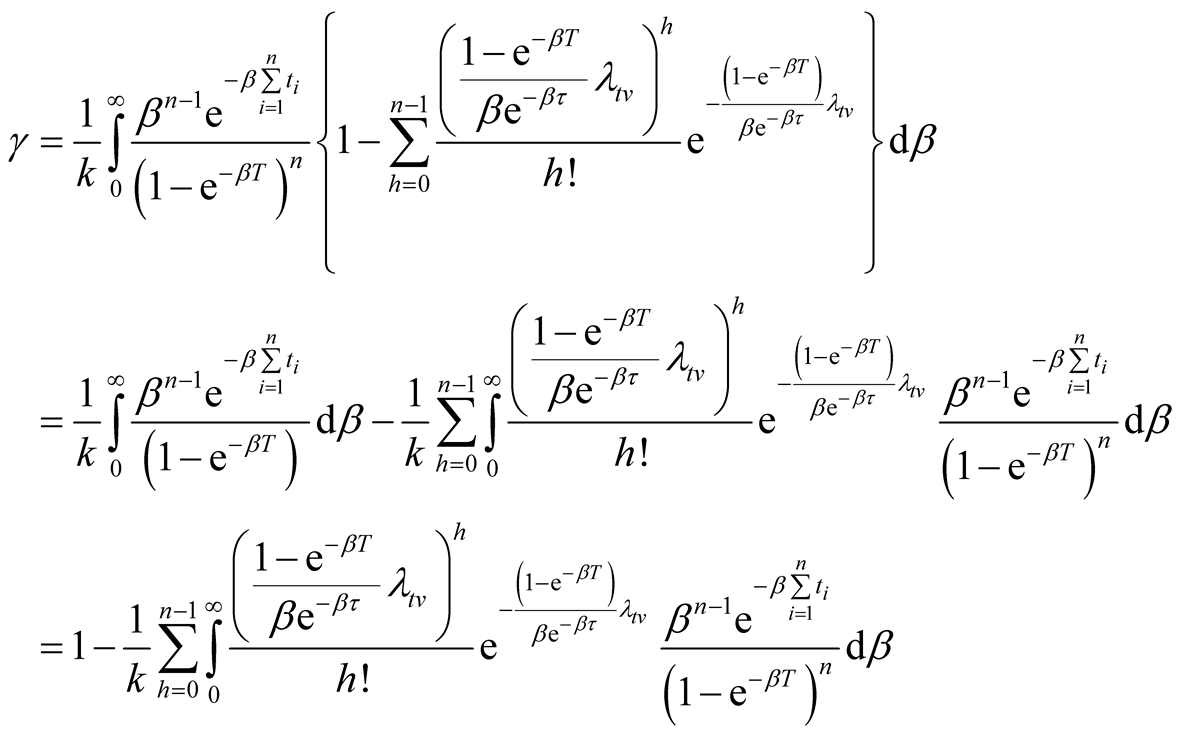 (A.12)
(A.12)
Equation (A.12) implies the second formula of Equation (13).
Proof of Proposition 3: For given level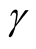 , the time required to attain the target value
, the time required to attain the target value 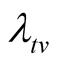 is
is  where
where  satisfies Equation (A.8). When
satisfies Equation (A.8). When  is known, from Equation (A.9), it can easily be seen that
is known, from Equation (A.9), it can easily be seen that
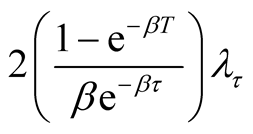 follows a chi-square distribution with
follows a chi-square distribution with 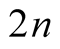 degrees of freedom. Therefore, we have
degrees of freedom. Therefore, we have
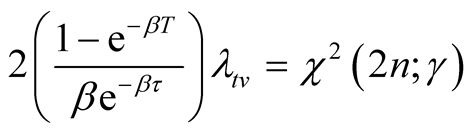 (A.13)
(A.13)
and Equation (14) follows immediately. We can obtain (ii) by following similar arguments given in the proof for the second part of Proposition 2.
Proof of Proposition 4: For a pre-determined 
 , the Bayesian Upper Prediction Limit (UPL) for
, the Bayesian Upper Prediction Limit (UPL) for  with level
with level  is
is 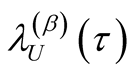 satisfying
satisfying . From Equation (A.8) and Equation (A.13)
. From Equation (A.8) and Equation (A.13)
we have . This implies that
. This implies that
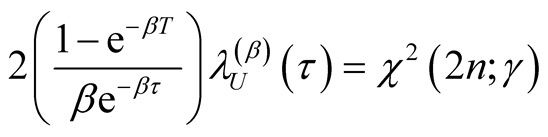 (A.14)
(A.14)
Making  the subject from Equation (A.14) we arrive at
the subject from Equation (A.14) we arrive at
 (A.15)
(A.15)
Equation (A.15) is the exact formula in Equation (17).
The formula in Equation (18) can be obtained by similar arguments.