A Scalar Compromise Equilibrium for N-Person Prescriptive Games ()
1. Introduction
Game theory is the study of strategic interactions among agents called players. Ultimately it involves a solution concept to describe, predict, or prescribe the choices of these players [1] . Modern game theory [2] [3] is predominantly noncooperative and assumes that any joint rational action by the players must necessarily be a Nash Equilibrium (NE) [4] [5] . In other words, rational players are assumed to be selfish. They act in their individual self-interest in the sense that each player considers his best responses to the possible joint actions of the other players. The result is that no player can improve his expected payoff in an NE by unilaterally changing his pure or mixed strategy. Various refinements of the NE (see [2] [3] , for example) have been proposed, yet the NE does not suffice for all strategic interactions. Social dilemmas [6] [7] illustrate that selfish behavior may conflict with group interests. For example, in Prisoner’s Dilemma each player can do better by cooperating.
In this paper we consider one-shot, n-person games in normal form. A player is considered rational if his strategy choices are consistent with some underlying decision-making criterion. For example, instead of being greedy, a player may be satisfied with a certain level of payoff. To provide a theoretical framework for such cases, we define a scalar equilibrium (SE) in which a scalar transformation modeling the decision criterion assigns scalar values in [0,1] to the outcome of each joint action of the players. An SE is a joint action maximizing these scalar values.
SEs address three problematic areas of noncooperative game theory.
1) SEs do not require that rationality be defined by selfish behavior.
2) An SE consists of pure strategies for each player, as opposed to mixed strategies that are difficult to interpret and implement [8] .
3) NEs are difficult to compute [9] , while SEs can be quickly obtained by simply finding the maximum of a finite number of scalar values.
SEs are particularly applicable (a) when all players have the same notion of rationality or (b) when an external arbiter dictates each player’s strategy according to some predetermined decision criteria. In case (a) the SE is descriptive or predictive—or possibly normative in the sense that it suggests actions for the players. In case (b), which is emphasized here, the SE is prescriptive.
The paper is organized as follows. In Section 2 we formally define the SE. In Section 3 we illustrate SEs with the compromise equilibrium (CE) and establish its Pareto optimality. In Section 4 we present some examples of two-person games and compare the CE with other solution concepts. Finally, in Section 5 we offer conclusions and discuss future research.
2. Scalar Equilibrium
Let 
denote an n-person, one-shot prescriptive game in normal form, where
is the set of players, 
is the finite set of pure strategies for player 
is the von Neumann-Morgenstern (VMN) utility of player 
for a pure strategy profile 
for all players, and 
A is an arbiter who assigns strategies for the players in their one-shot.
A need not be a person. The arbiter could be a common decision criterion applied by the n players. The arbiter could be a licensing agreement for the licensees of a patent, for example. It could be a computer algorithm for making real-time decisions on a website where the players have agreed to its terms and conditions. In the current regulatory spirit, it could also be a policy imposed by a national governmental agency on some segment of the population. In other words, an arbiter is a prescriptive agent.
Regardless, A’s decision criterion for assigning strategies can be represented by an ordinal utility function
(see [10] [11] ) that induces a preference relation 
on 
For 
we write
if 
if 
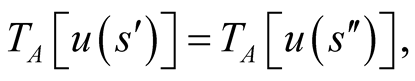and 
if either 
or 
A is said to be indifferent between 
and 
if
Thus A may be considered rational in the sense that 
is complete and transitive.
Definition 2.1. The pure strategy profile 
is an SE for 
if and only if 
for all
Thus 
is an SE if it maximizes the scalar composite function 
over 
If 
has multiple SEs resulting from ties in the maximization of Definition 3.1, it is assumed that A will choose one 
from the SEs by some further mechanism.
3. Compromise Equilibrium
The compromise equilibrium CE for 
is now presented as an example of an SE. Since 
is a finite set of pure strategies for each player, 
is bounded. We write 
and 
for
Now for all 
define the transformation 
by
(1)
Note that 
for all 
The number 1 in the numerators of Equation (1) prevents
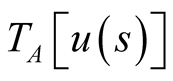from being 0 for an 
for which 
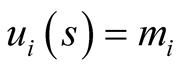for some i, while the 1 in the denominators prevent a division by 0 for an i for which 
The intuition behind Equation (1) is explained as follows. If we maximize the function 
over the region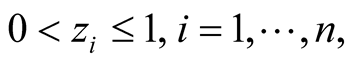 
the maximum is given by
Similarly, maximizing Equation (1) yields a CE 
for which the terms 
are large and close in value for those 
for which
Otherwise 
Thus if an arbiter A applies Equation (1), the players with 
will receive payoffs in roughly the same percentile of their payoff ranges. If maximizing 
is the decision criterion for all players (with ties broken by some further mechanism), the outcome can be construed as an equitable compromise between the players’ selfishness and unselfishness. A CE, however, differs substantially from the Rabin’s fairness equilibrium [12] for two players and from other notions of fairness as presented in [13] .
Any CE is also a Pareto optimum [14] of 
which is essential for a solution concept to an n-person game [15] . For example, a pure NE not Pareto optimal cannot be a joint rational solution since an alternate strategy profile can improve some players’ payoffs without diminishing anyone’s.
Definition 3.1. The pure strategy profile 
dominates 
if and only if 
for
and 
for some 
A pure strategy profile 
is Pareto optimal for 
if 
is not dominated by any 
Lemma 3.2. For any 
if 
dominates 
then 
Proof. Let 
and suppose that 
dominates 
From Definition 3. 1 it follows that
for all 
and 
for some index j. Thus for 
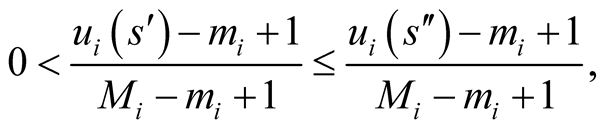(2)
and for 
(3)
Together Equation (2) and Equation (3) give
so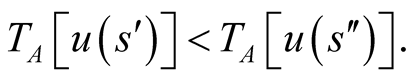 
Theorem 3.3. If 
is a CE for 
then 
is Pareto optimal for 
Proof. Let 
be a CE for 
We prove the contrapositive. If 
is not Pareto optimal, there exists
that dominates 
From Lemma 3.2 it follows that 
so 
is not a CE for 
4. Examples
We now present two examples for 
to illustrate the CE. For 
calculations using Equation (1) are similar. In the examples, we compare the CE to any pure NE, where each player’s action selfishly maximizes his payoff for the action of the other player. We also compare CEs to any mutual-max outcome [12] , where each player unselfishly maximizes the payoff for other player’s action. Finally, we compare CEs to maximin outcomes [2] in which each player’s action maximizes his minimum payoff resulting from the actions of the other players.
Example 4.1. Consider the Prisoner’s Dilemma (PD) payoff matrix of Figure 1, where D denotes the action “Defect” and C denotes “Cooperate”. The pure NE is (D, D), the mutual-max outcome is (C,C), and the maximin outcome is (D, D). The matrix of values calculated from Equation (1) is shown in Figure 2, from which the Pareto optimum (C, C) is the unique CE. Note that the mutual-max outcome and the CE are the same.
Example 4.2. Consider now the discoordination game [16] given by Figure 3. Players 1 and 2 approach each other. Player 1’s incentive is to veer right (R) or left (L) in the opposite direction from Player 2’s move. However, Player 2’s incentive is to encounter Player 1. There is no pure NE or mutual-max outcome for this game. The maximin outcome is (R, R). The CE scalar values are shown in Figure 4, with the unique CE being the Pareto optimum (R, R). The maximin outcome is the same as the CE.
5. Conclusions
In this paper the general notion of a scalar equilibrium SE is defined for an n-person, one-shot game in normal form. The advantages of an SE include flexibility in the decision criteria for decision makers, the selection of pure strategies for the players, and the speed of computing an SE. An SE is most applicable when the games are prescriptive, i.e., when an arbiter A assigns the players’ actions for their one shot.
The compromise equilibrium CE is presented here as a special case of an SE. Significantly, a CE is also a Pareto optimal pure strategy profile for the VNM utilities. It may be interpreted as a reasonable tradeoff of payoffs
imposed on the players by the arbiter A. Future research should explore other SEs. For example, one might define a transformation 
to obtain an SE approximating a pure NE when one does not exist.
NOTES
*Corresponding author.