1. Introduction and Statement of Results
Let  be a polynomial of degree n such that
be a polynomial of degree n such that
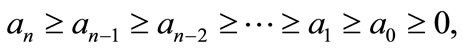
then according to a classical result usually known as Eneström-Kakeya theorem [11], 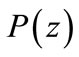 does not vanish in
does not vanish in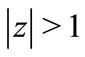 . Applying this result to the polynomial
. Applying this result to the polynomial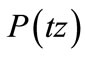 , the following more general result is immediate.
, the following more general result is immediate.
Theorem A. If  is a polynomial of degree n such that for some
is a polynomial of degree n such that for some 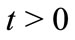
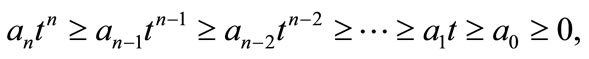
then has all the zeros in
has all the zeros in .
.
In the literature, [1-15], there exist extensions and generalizations of Eneström-Kakeya theorem. Joyal, Labelle and Rahman [9] extended this theorem to polynomials whose coefficients are monotonic but not necessarily non negative and the result was further generalized by Dewan and Bidkham [6] to read as:
Theorem B. If  is a polynomial of degree n such that for some
is a polynomial of degree n such that for some  and
and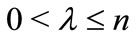 ,
,
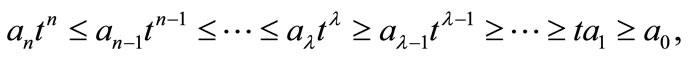
then  has all the zeros in the circle
has all the zeros in the circle
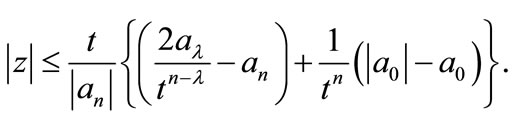
Govil and Rahman [8] extended Theorem A to the polynomials with complex coefficients. As a refinement of the result of Govil and Rahman, Govil and Jain [7] proved the following.
Theorem C. Let  be a polynomial of degree n with complex coefficients such that for some
be a polynomial of degree n with complex coefficients such that for some 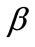
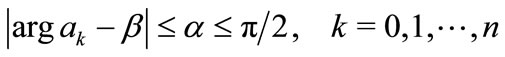
and

then  has all its zeros in the ring-shaped region given by
has all its zeros in the ring-shaped region given by
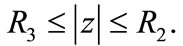
Here

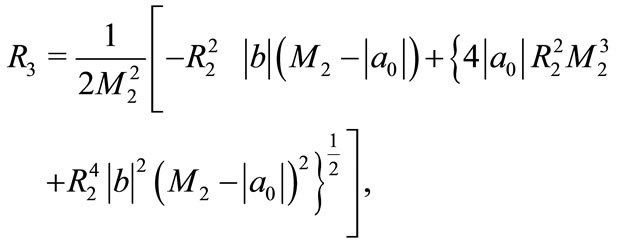
where
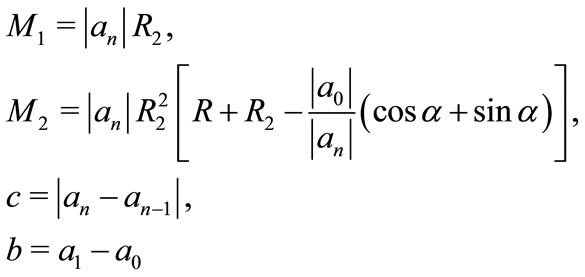
and
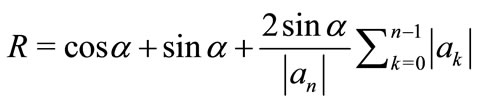
By using Schwarz’s Lemma, Aziz and Mohammad [1] generalized Eneström-Kakeya theorem in a different way and proved:
Theorem D. Let  be a polynomial of degree n with real positive coefficients. If
be a polynomial of degree n with real positive coefficients. If  can be found such that
can be found such that

where  then all the zeros of
then all the zeros of  lie in
lie in .
.
In this paper, we also make use of a generalized form of Schwarz’s Lemma and prove some more general results which include not only the above theorems as special cases, but also lead to a standard development of interesting generalizations of some well known results. Infact we prove Theorem 1. Let  be a polynomial of degree n such that
be a polynomial of degree n such that
 where
where  and
and ,
,  are real numbers and for certain non negative real numbers
are real numbers and for certain non negative real numbers 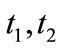 with
with  and
and 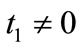
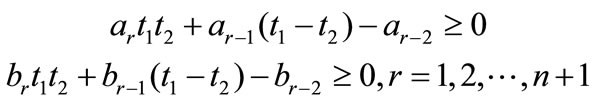
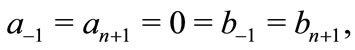
then all the zeros of  lie in
lie in
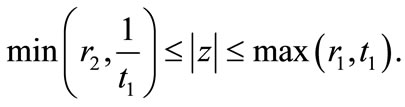
Here


where

Assuming that all the coefficients 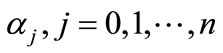 are real, the following result is immediate:
are real, the following result is immediate:
Corollary 1. Let  be a polynomial of degree n with real coefficients such that for certain non negative real numbers
be a polynomial of degree n with real coefficients such that for certain non negative real numbers ,
,  with
with 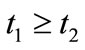 and
and 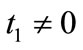
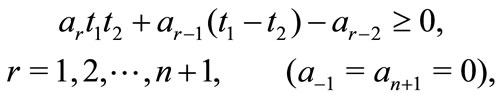
then all the zeros of  lie in
lie in
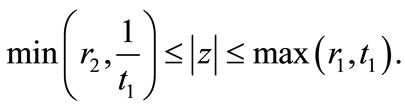
Here
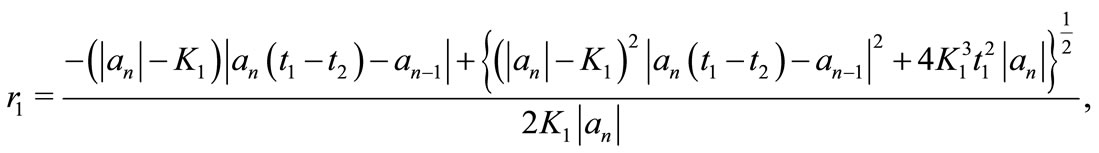
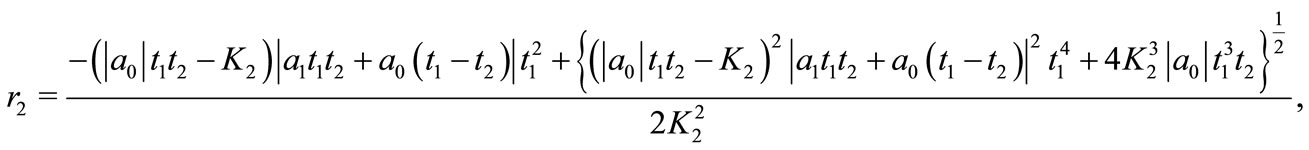
where
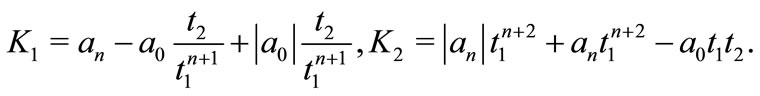
If in Corollary 1, we assume that all the coefficients are positive and  then we have the following:
then we have the following:
Corollary 2. Let  be a polynomial of degree n such that for some real number
be a polynomial of degree n such that for some real number 
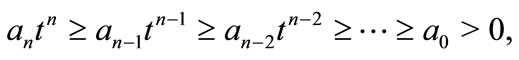
then all the zeros of  lie in
lie in
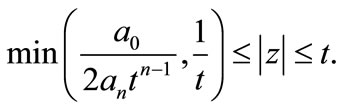
In particular, if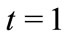 , Corollary 2 gives the following improvement of Eneström-Kakeya theorem.
, Corollary 2 gives the following improvement of Eneström-Kakeya theorem.
Corollary 3. Let  be a polynomial of degree n such that
be a polynomial of degree n such that
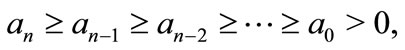
then all the zeros of  lie in
lie in

We next prove the following more general result which include many known results as special cases.
Theorem 2. Let 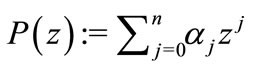 be a polynomial of degree n such that
be a polynomial of degree n such that  where
where  and
and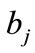 ,
,  are real numbers. If
are real numbers. If  can be found such that for a certain integer
can be found such that for a certain integer ,
, 

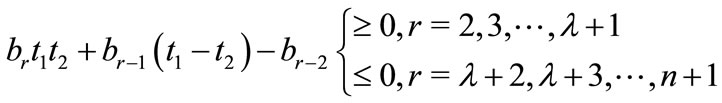
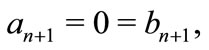
then all the zeros of  lie in
lie in
 (1)
(1)
where
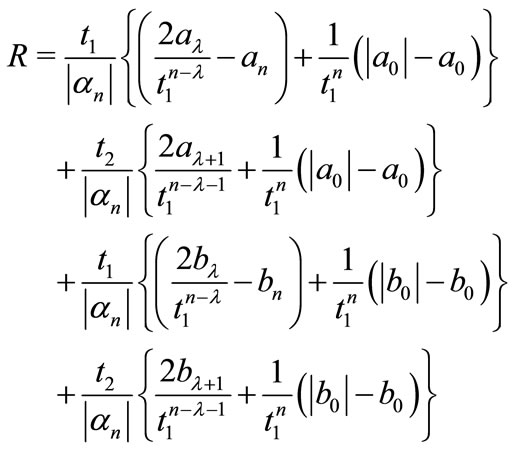
Remark 1. Theorem B is a special case of Theorem 2, if we take 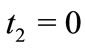 and assume that all the coefficients
and assume that all the coefficients ,
,  are real.
are real.
The following result follows immediately from Theorem 2 by taking  and assuming
and assuming ,
,  to be a real.
to be a real.
Corollary 4. Let  be a polynomial of degree n with real coefficients. If
be a polynomial of degree n with real coefficients. If  can be found such that
can be found such that

then all the zeros of 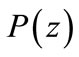 lie in
lie in

Remark 2. For  and
and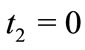 , Corollary 4 reduces to a result of Joyal, Labelle and Rahman [9].
, Corollary 4 reduces to a result of Joyal, Labelle and Rahman [9].
We also prove the following result which is of independent interest.
Theorem 3. Let  be a polynomial of degree n such that
be a polynomial of degree n such that 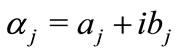 where
where  and
and ,
,
 are real numbers. If
are real numbers. If  can be found such that for a certain integer
can be found such that for a certain integer ,
, 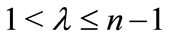
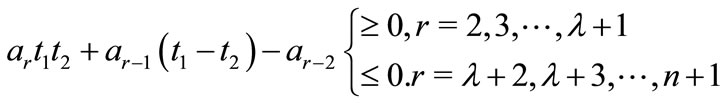
and
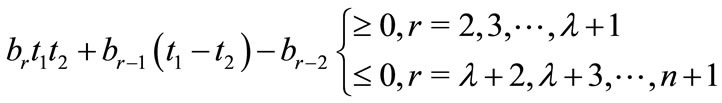
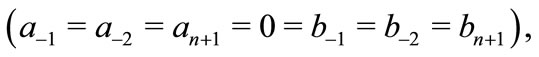
then all the zeros of  lie in
lie in
 (2)
(2)
where
 .
.
Remark 3. Theorem 4 of [4] immediately follows from Theorem 3 when ,
,  and the coefficients
and the coefficients ,
,  are real.
are real.
On combining Theorem 2 and Theorem 3 the following more interesting result is immediate.
Corollary 5. Let  be a polynomial of degree n such that
be a polynomial of degree n such that  where
where  and
and ,
, 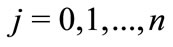 are real. If
are real. If  can be found such that for a certain integer
can be found such that for a certain integer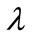 ,
, 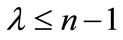
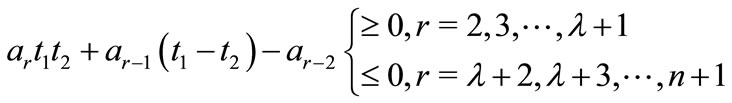

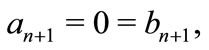
then all the zeros of  lie in the intersection of the two circles given by (1) and (2).
lie in the intersection of the two circles given by (1) and (2).
If we take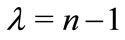 and the coefficients
and the coefficients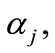
 are real in Theorem 3, we get the following result.
are real in Theorem 3, we get the following result.
Corollary 6. Let  be a polynomial of degree n with real coefficients. If
be a polynomial of degree n with real coefficients. If  can be found such that
can be found such that

then all the zeros of  lie in
lie in
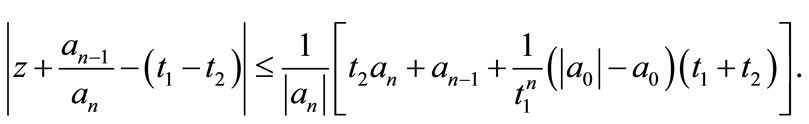
The following result also follows from Theorem 3, when , the coefficients
, the coefficients ,
,  are real and
are real and .
.
Corollary 7. Let  be a polynomial of degree n with real coefficients. If for some
be a polynomial of degree n with real coefficients. If for some ,
,

then  has all the zeros in
has all the zeros in
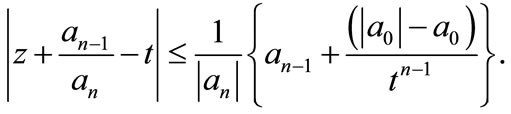
2. Lemmas
For proving the above theorems, we require the following lemmas. The first Lemma which we need is due to Rahman and Schmeisser [11].
Lemma 1. If  is analytic in
is analytic in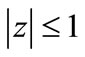 ,
, , where
, where ,
, 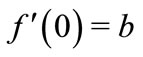 ,
, on
on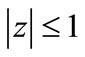 , then for
, then for ,
,
 From Lemma 1, one can easily deduce the following :
From Lemma 1, one can easily deduce the following :
Lemma 2. If  is analytic in
is analytic in ,
,  ,
, 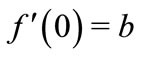 and
and  for
for , then
, then
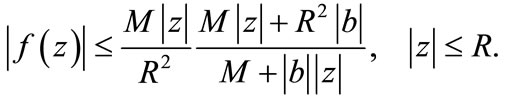
The next Lemma is due to Aziz and Mohammad [2].
Lemma 3. Let ,
, 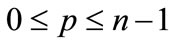 be a polynomial of degree n with complex coefficients.
be a polynomial of degree n with complex coefficients.
Then for every positive real number r, all the zeros of  lie in the disk
lie in the disk
 (3)
(3)
3. Proofs of the Theorems
Proof of Theorem 1. Consider the polynomial
 (4)
(4)
Further, let
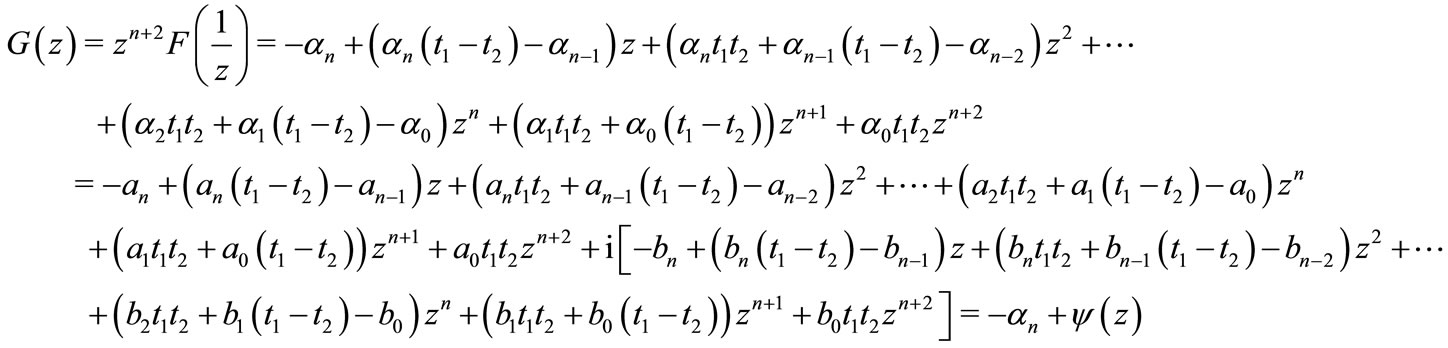 (5)
(5)
where
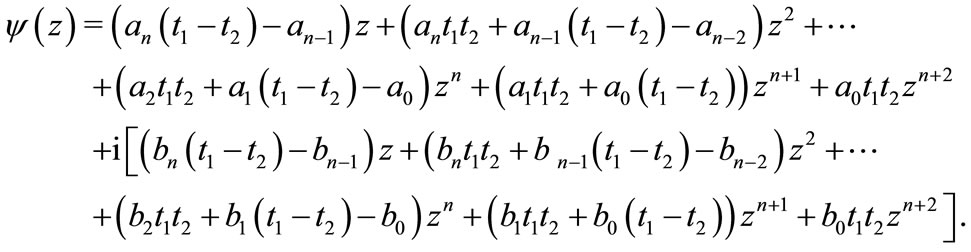
Now

This gives after using hypothesis, for 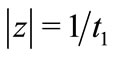
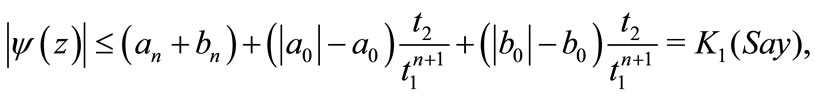
Clearly,  and
and

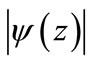 for
for 
Thus, it follows by Lemma 2 that
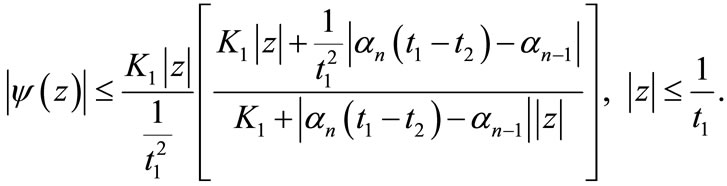
From (5), we get
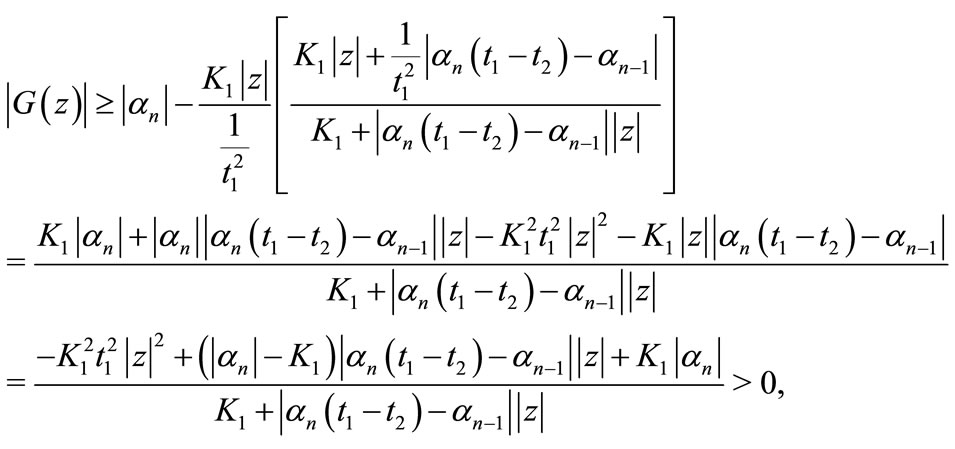
if
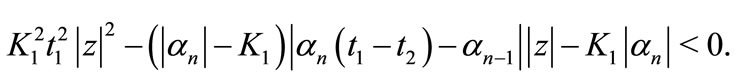
This gives  if
if

Consequently, all the zeros of  lie in
lie in

Since , it follows that all the zeros of
, it follows that all the zeros of  and hence all the zeros of
and hence all the zeros of  lie in
lie in
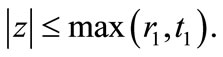 (6)
(6)
Again from (4)
 (7)
(7)
where
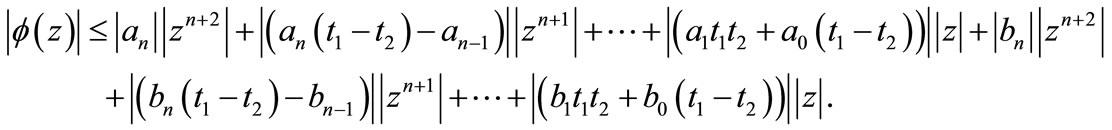
Therefore, for , we have by using the hypothesis
, we have by using the hypothesis
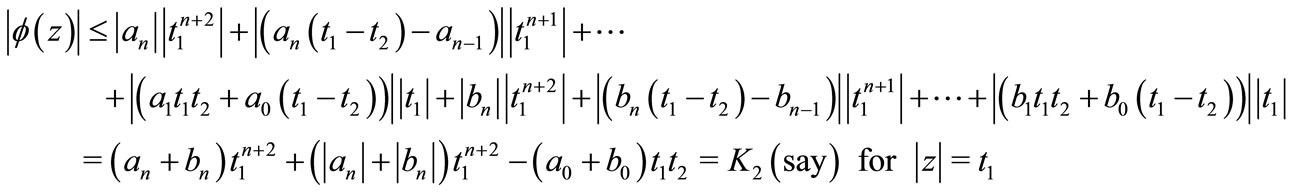
Therefore, it follows again by Lemma 2 that

Using this result in (7), we get

if
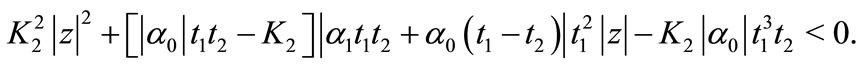
Thus  if
if
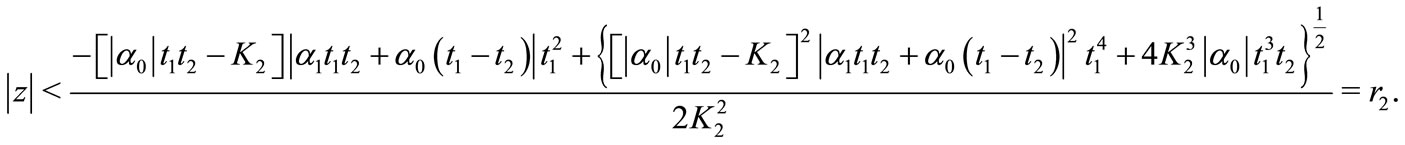
This shows that all the zeros of  and hence of the polynomial
and hence of the polynomial  lie in
lie in
 (8)
(8)
Combining (6) and (8), we get the desired result.
Proof of Theorem 2. Consider the polynomial

Since 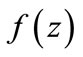 is a polynomial of degree n + 2, it follows by applying Lemma 3 to
is a polynomial of degree n + 2, it follows by applying Lemma 3 to  with
with  and
and , that all the zeros of
, that all the zeros of  lie in
lie in
 (9)
(9)
Now

Using the hypothesis, we get

Hence by (9) all the zeros of  lie in the circle
lie in the circle where
where
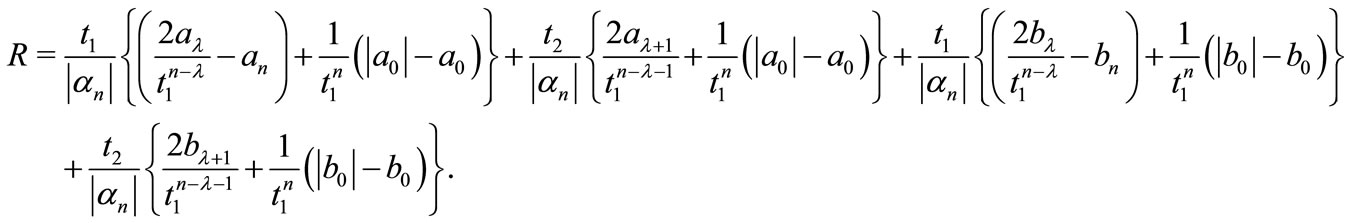
Since every zero of 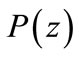 is also a zero of
is also a zero of , the theorem is proved completely.
, the theorem is proved completely.

This gives

Let  , we get by using the hypothesis
, we get by using the hypothesis

if
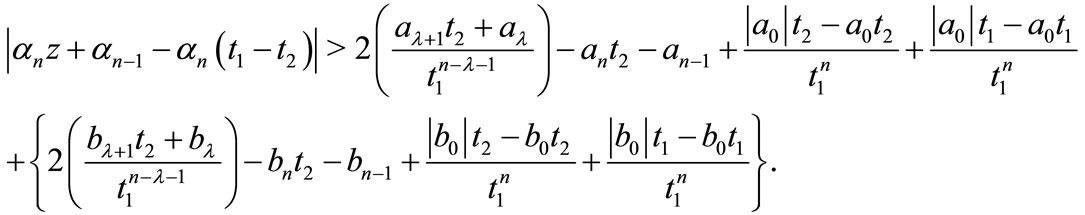
Thus  if
if

T his shows that those zeros of  whose modulus is greater than
whose modulus is greater than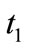 , lie in the circle
, lie in the circle
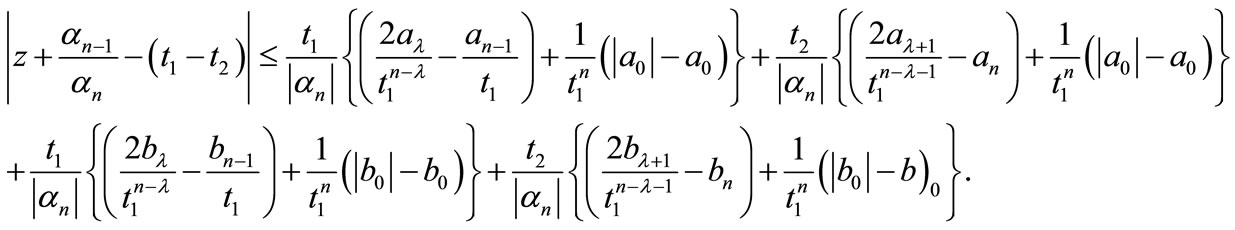
It can be easily verified that those zeros of  whose modulus is less than
whose modulus is less than , lie in the circle as well. Therefore, we conclude that all zeros of
, lie in the circle as well. Therefore, we conclude that all zeros of  and hence
and hence 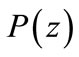 lie in
lie in
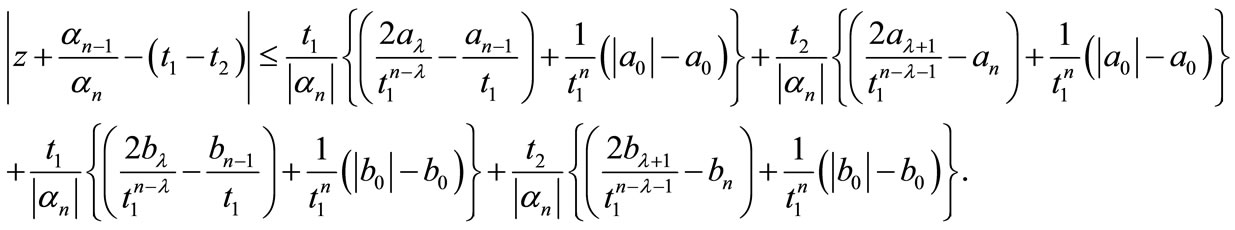
This completes the proof of the theorem.