The role of catalysis on the formation of an active proto-enzyme in the prebiotic aqueous environment ()
1. INTRODUCTION
This work aims to discuss, on the basis of known chemistry, if the prebiotic conditions on Earth could allow for the spontaneous formation of catalytic polypeptides without any prior complex RNA-based chemistry that could code for enzymes with specific amino acid sequences. After the formation of proto-enzymes we may envision the development of a more complex chemistry until a kinetic cycle of reactions involving self-replicating species was reached. We assume a source of amino acids sustained by processes driven by an energy source acting on simple organic compounds and focus on the formation of peptide bonds among amino acid units until the critical length that allows for catalytic properties is attained. It will be shown that the length of the polypeptide depends on how many types of monomeric units are involved in the formation of the chain. There are a number of simulations of the processes taking place in interstellar ices showing how many amino acids may form from simple organic molecules. For example Muñoz Caro et al. [1] have shown the formation of 16 amino acids by UV irradiation of ices with components H2O, CO, CO2, CH3OH and NH3. Maurette [2] suggested that micrometeorites could have acted as chemical reactors forming amino acids from organic precursors upon contact with water and warm temperatures following re-entry. However, given the degree of uncertainty of the actual processes that have formed primordial amino acids, we choose to keep the number of amino acids as a variable and regard direct sources of amino acids as equivalent to sources of their precursors. Since it has been shown that a hydrosphere was interacting with the Earth’s crust as early as 4.3 Gyr ago [3], we may also safely assume that the polymerization process took place in the terrestrial aqueous environment, with or without the participation of solid surfaces promoting the peptide bond formation [4,5]. A similar approach was undertaken by Chen and Nowak [6] that investigated the equilibrium configuration of RNA polymers formed from activated monomers and exhibiting self-replication and selection.
It has been well established that micrometeorites, interplanetary dust particles (IDP), and carbonaceous chondrites presently deliver amino acids to the Earth [7]. Larger bodies also exhibit significant inbound fluxes, but the heating experienced during the atmospheric entry and impact phases is likely to pyrolyze their organic content. The flux of IDPs has been estimated around 3.0 × 107 kg∙yr−1 [8] and the content of amino acids in polar micrometeorites has been reported to be 180 - 249 ppm [9] and up to 869 nmol/g [8]. Micrometeorites could thus deliver 2.61 × 104 mol∙yr−1 of amino acids, a figure that must be multiplied by a factor of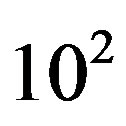 
to 
based on the lunar cratering record of 3.8 to 4.5 Gyr ago [10]. Wilson [11] estimates a flux of 3.6 × 1010 kg∙yr−1 of organic carbon in IDPs that were subjected to mild temperatures and survived re-entry on the early Earth. The oceanic amino acid concentration from electrical discharge and cometary input 4 Gyr ago was estimated by Pierazzo and Chyba [12] to be 2.4 × 10−9 M and 1.5 × 10−11 M for glycine and aspartic acid, respectively.
The extent of the amino acid source is both critical to the formation of long polypeptide chains and to their concentration. This investigation begins by determining the (small) concentration of polypeptides of given lengths in equilibrium conditions, i.e. in the absence of amino acid sources. It will proceed to examine the effect of a source and catalysis on the dynamics of the state variables (concentrations of all the polymers of different lengths), determining also the time scale for achieving steady-state conditions. The maximum length of the polypeptides at steady-state will also be determined, a key factor strictly related to their potential catalytic capabilities.
The concentration of the amino acid monomers will be expressed in terms of the intensity of the source or, equivalently, of the incoming flux. Having determined the connection between the concentration of polypeptides of a given length and the steady-state concentration of monomers, we will be able to express the lengths of the polypeptides in terms of the source intensity, the size of the amino acid set, and the parameters governing the reactivity of the peptide bond, i.e. bond formation and hydrolysis.
2. RESULTS AND DISCUSSION
An evolutionary process able to build an active enzyme with n amino acid residues from its monomeric components must have produced nearly all the possible polypeptides of length n. It has been determined experimentally that, in order to retain the catalytic activity of an enzyme, a fraction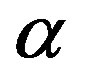 
between 0.1 and 0.2 of its amino acid sequence is constrained [13]. Within this requirement, the number of possible proteins with n aminoacid residues chosen from a set of 
aminoacids is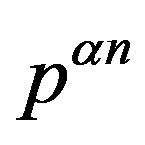
. The ratio between the oceanic content of all the polypeptides of length n and the total number of possible structures of the same length is
(1)
where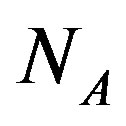 
is the Avogadro number and 
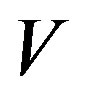is the volume of water on the planetary body hosting the prebiotic chemistry. In the assumption that a catalytic protein did form in the prebiotic environment, we must have 
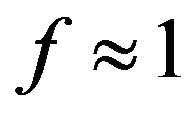and Eq.1 constrains the value of 
once we determine
.
We begin considering a solution of total content c of amino acid monomers that reaches equilibrium with formation of dipeptides of concentration
, tripeptides of concentration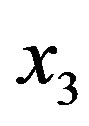
, and so forth, with 
indicating the concentration of the polypeptide with i components. The equilibrium constant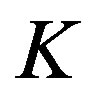 
is assumed to be independent of i. We have thus
(2)
that iteratively gives
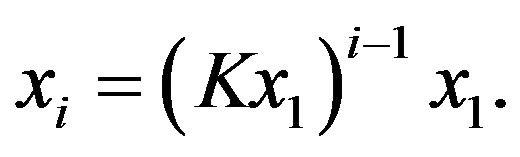(3)
The mass balance equation links the concentration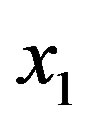 
to the total amino acid content and the equilibrium constant
(4)
Since the reactants and products have nearly the same free energy [5], we have
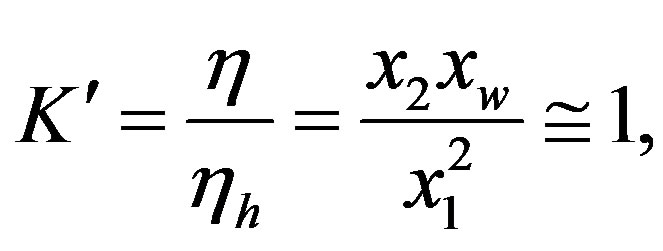(5)
with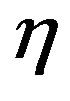 
being the bimolecular rate coefficient for peptide bond formation and 
the rate coefficient for hydrolysis. The concentration of water 
is usually included in the equilibrium constant obtaining
, which makes 
in Eq.4 very small (we are considering dilute solutions) and gives, to a very good approximation, 
, making the concentration of all the polypeptides given by Eq.3 virtually negligible
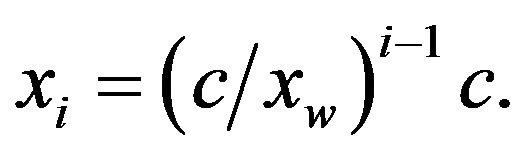(6)
It is thus necessary, to increase the concentration of polypeptides of significant lengths, that the system be endowed with a source of amino acids. This source can be thought of as either external (meteoritic and cometary impacts, IDPs) or internal to the biosphere. High temperatures in hydrothermal vents [14] and electrical discharge in the atmosphere [16] are thought to be viable spontaneous processes that were able to form amino acids from simple compounds and to have provided 1010 kg∙yr−1 of organics [16] and 107 kg∙yr−1 of amino acids. In the hypothesis that the system evolved in the presence of a source with the ability to keep the concentration of monomers 
constant, the rate of spontaneous formation of a dipeptide between two aminoacid monomers of molar concentration
is
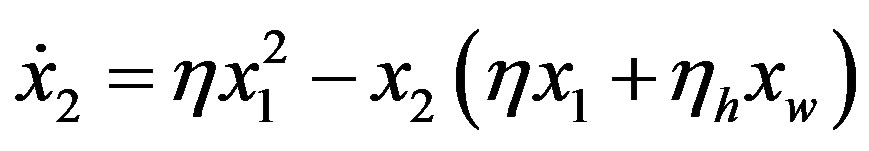(7)
(the formation of 
by hydrolysis of 
is being neglected). The quantity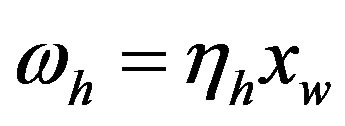 
is a constant because of the large excess of water, and its experimental value for the hydrolysis of glycyl-glycine is 6.3 × 10−11 s−1 [17]. It is useful to define the proper frequency of the reactive system as
(8)
and the ratio 
of the rates of peptide formation and the overall reaction (peptide formation plus hydrolysis)
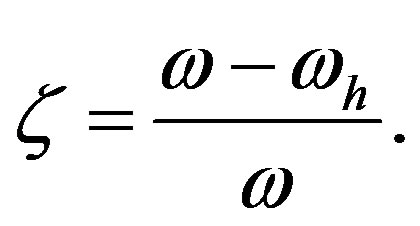(9)
Consequently, the ratio between the rates of the catalyzed and uncatalyzed reactions is
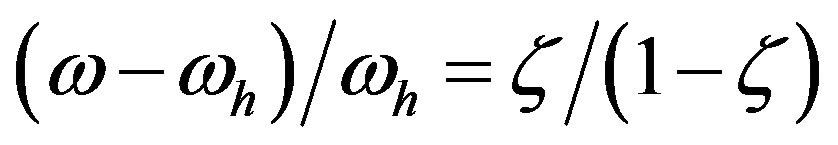. The values taken by the parameter 
describe all the possible relative rates; for example, 
means equal rates for peptide bond formation and hydrolysis, while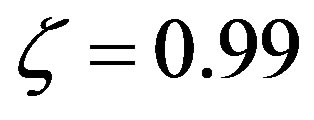 
represents a ratio of the rates of 99.With the previous definitions, the solution of Eq.7 is
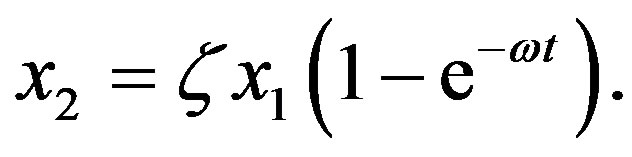(10)
For the formation of peptides with three residues we thus have
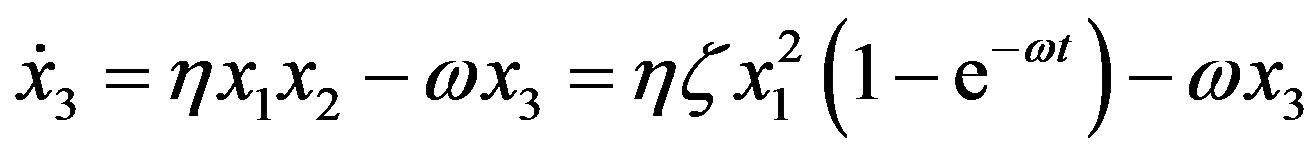(11)
with solution
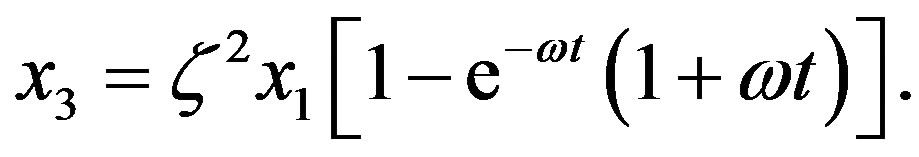(12)
This procedure can be iterated and one obtains for the formation of the peptide with n residues the equation
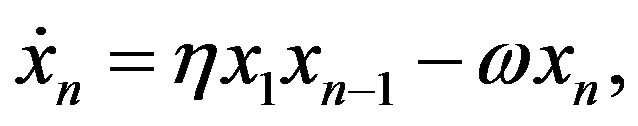(13)
with solution
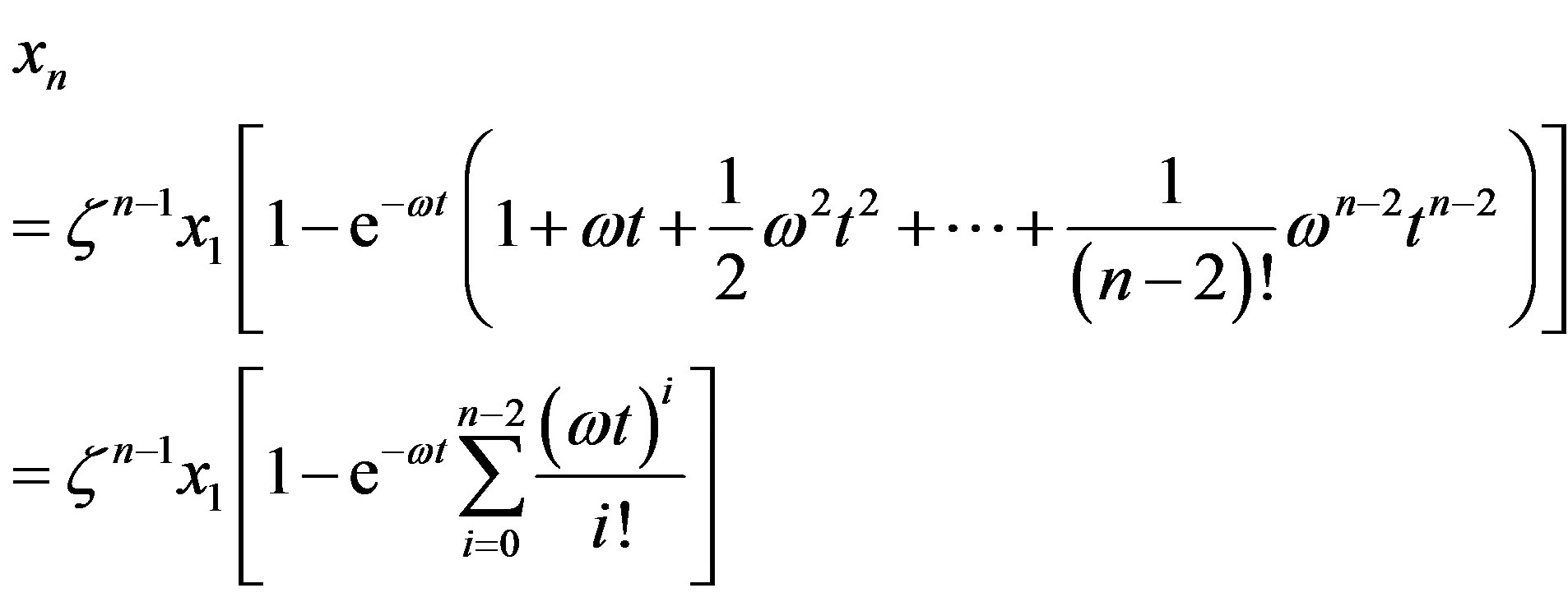(14)
Given the definition of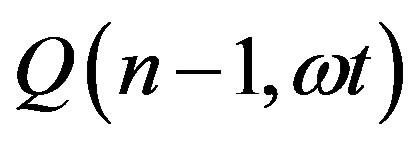 
as the ratio between the incomplete and complete gamma function of Euler
(15)
we may more conveniently express 
as
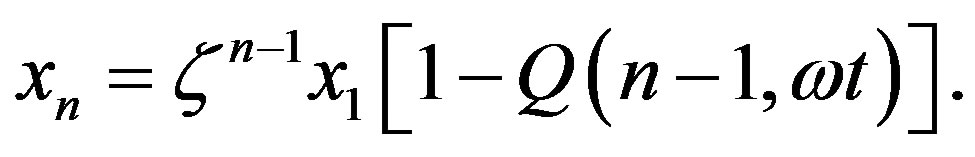(16)
The inflection point of 
located at 
separates the early from the late stages of polypeptide formation, the latter being close to the stationary state. We now define the number of molecules of the monomer at stationary state 
and equate the r.h.s of Eq.16 to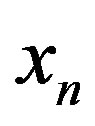 
from Eq.1, obtaining the evolution equation for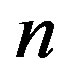 
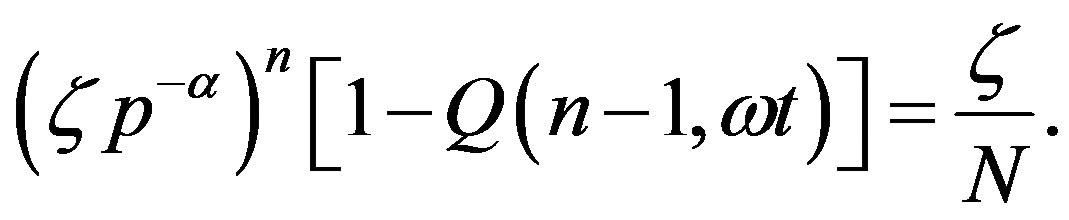(17)
Numerical solutions of Eq.17 are shown in Figure 1 for two values of
. The curve with
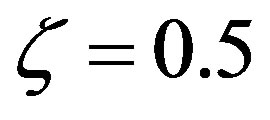, corresponding to the already fairly large ratio
, affords polypeptides with lengths limited to 80 amino acid units. The curve defined by 
shows that the catalytic efficiency necessary to attain polypeptide lengths of 241 units implies
, that is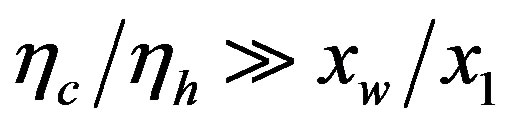 
.
The elapsed proper time before steady-state is also dependent on the ability of the environment to catalyze peptide bond formation. In fact, since in the absence of catalysis the ratio of the rate coefficients for peptide formation and hydrolysis is about unity (the reaction is nearly thermoneutral), and we may reasonably assume that the concentration of amino acids is much lower than that of water
, we have 
and
(18)
On the contrary, in the presence of significant catalysis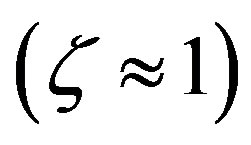
, the proper frequency is dominated by the polymerization process.
We may now estimate that the uncatalyzed reacting system may attain steady state in the proper time
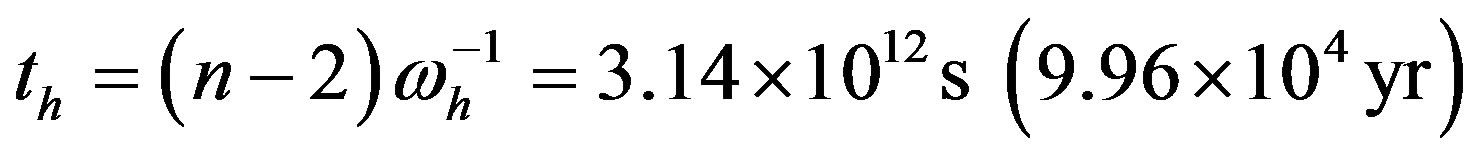, while the corresponding time for the catalyzed system would be lowered to
, showing that in both cases a steady state concentration of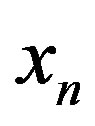 
is reached in the very early stages of the chemical evolution. These proper times may be compared to the much longer time (8 - 10 Myr) necessary for the volume of the sea to circulate through the hot areas of the intrusion zones in the sea floor [18, 19] and constituting a sink for the protoenzymes.
We now give two convenient approximate expressions of Eq.16 valid for small and large t, respectively. For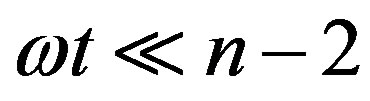
, we approximate 
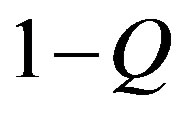as
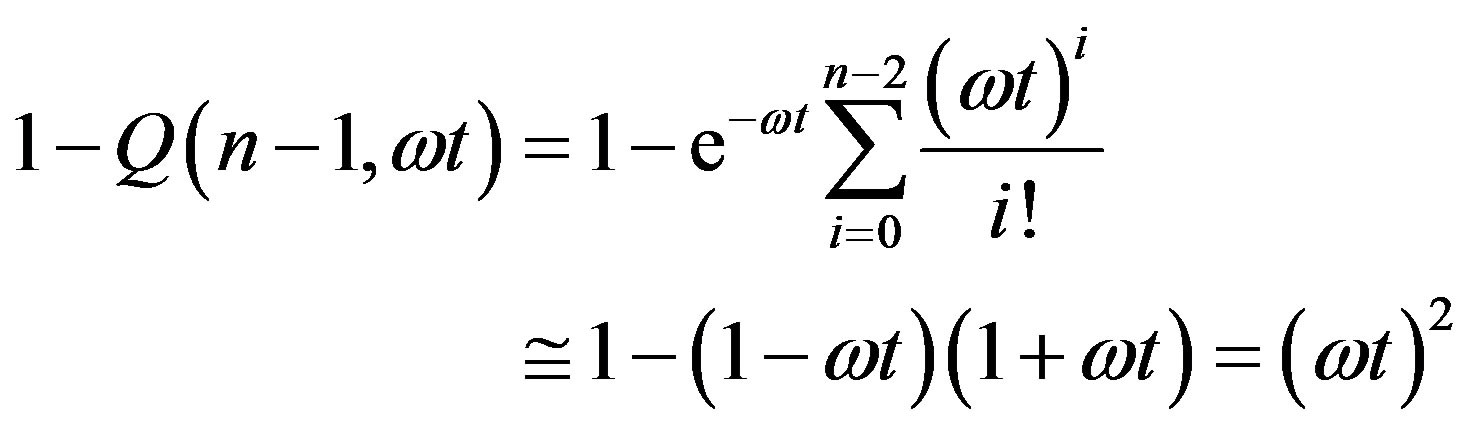(19)
and, for
,
(20)
that give the following approximation of Eq.16
(21)
where 
and 
for 
and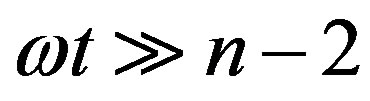
, respectively. For these two cases, Eq.17 has the closed-form solution
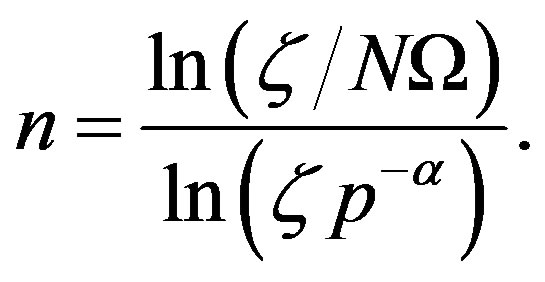(22)
The plots of Eq.22 given in Figure 2 for two typical values of the parameter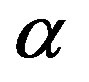 
show that a catalytic protein of significant length could only be formed in a catalyzed medium with 
and attest that in the absence of catalysis the length of the polypeptides is limited to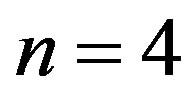
. Thus the catalytic capability of the spontaneously formed proto-enzymes, directly dependent on their size, strictly depends on the ratio of the rate coefficients for the peptide bond formation and hydrolysis, expressed through the parameter
.
Also, the steady state concentrations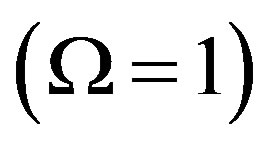 
of the polypeptides of length n differ markedly in the uncatalyzed system, where 
is given by Eq.18, and the catalyzed system, where 
approaches unity. In the uncatalyzed system the solution given by Eq.21 is very similar to the corresponding solution for the equilibrium problem Eq.6, while the effect of catalysis dramatically increases the concentration of long polypeptides by thelarge factor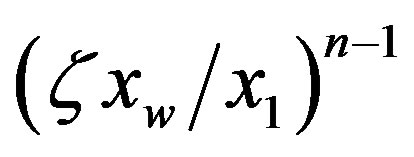
. Thus high values of 
in-
Figure 2. Effect of the catalytic efficiency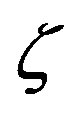 
on the number n of amino acid units constituting an enzyme at steady state according to Eq.22 for two typical values of the parameter α and the present-day volume of the sea. The effect of different values of the number of available amino acids is also shown: p = 20 (solid lines) and p = 10 (dashed lines).
crease both the length and the concentration of long polypeptides.
We now turn our attention to determine how the steady state concentration of the amino acid monomers changes with the source. Given a source s of amino acids, the evolution of the concentration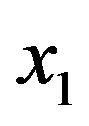 
is given by
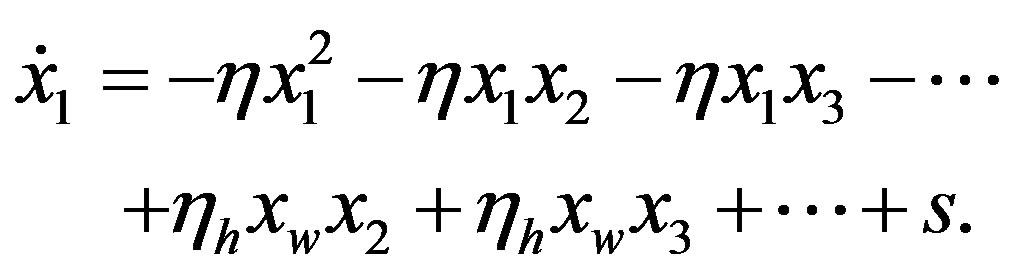(23)
The steady state condition is
(24)
For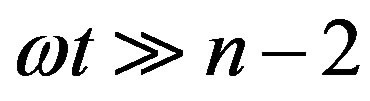
, Eq.21 holds with
, and we have
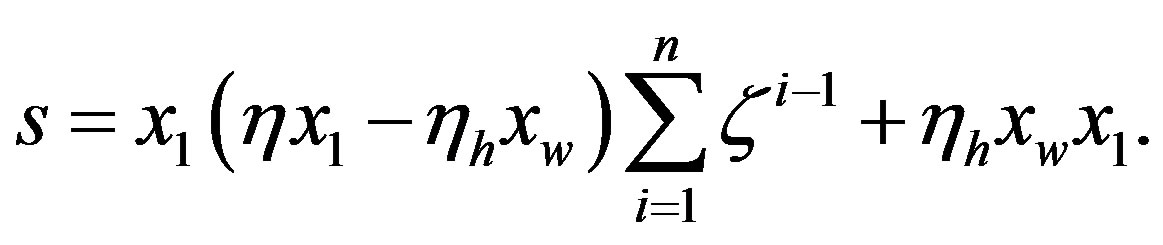(25)
We now define 
and obtain
(26)
the approximation being valid for large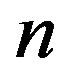
. Using this approximation and Eq.9, Eq.25 becomes
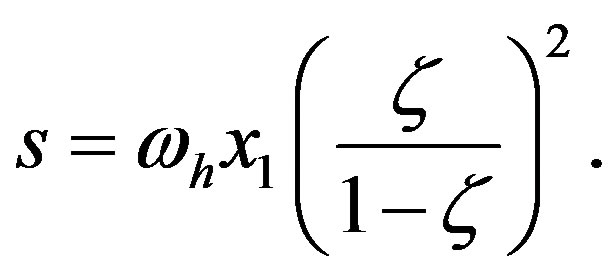(27)
The flux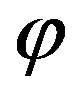 
of amino acids on the surface of the early Earth of radius 
and the corresponding source are related by
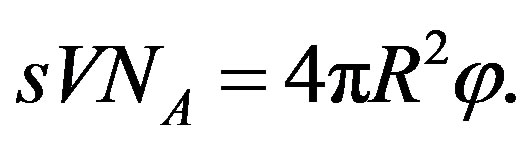(28)
Thomas [20] estimates the infall rate of organic carbon from interplanetary dust particles between 108 and 1010 kg∙yr−1, with an amino acid content around 3%. Assuming an average content of 10 carbon atoms per amino acid, the estimate made by Thomas translates into an infalling rate between 4.77 × 1023 and 4.77 × 1025 s−1 of amino acids. For the purpose of the following calculations we will make use of the average between these two values and the present-day volume of the sea (today the Earth has a water content of 1.4 × 1021 kg). This choice corresponds to the estimate of Pasek and Lauretta [21] of 
for the flux of carbon during the late heavy bombardment. With this estimate, Eq.27 gives for the catalyzed system with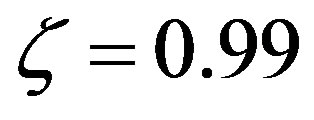 
a concentration of the amino acid monomers of
, and we obtain for the stationary-state number of molecules of the monomer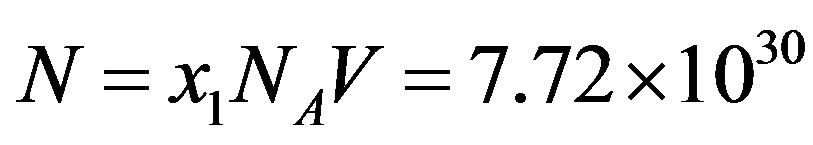
. Eq.21 in turns gives
.
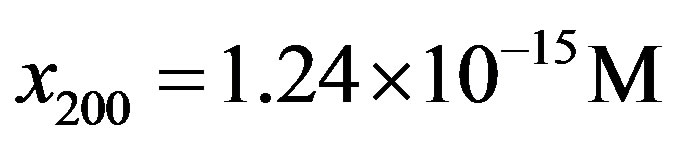We now have all the elements that link the fundamental quantities that play a role in the formation of a primordial catalyst. Eq.1 relates the concentration of a catalytic peptide of length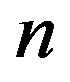
, the fraction 
of conserved residues, and the size of the amino acid set
. Eqs.21 and 27 connect 
to the catalytic efficiency 
for the formation of the peptide bond, the frequency of hydrolysis
, and the source of amino acid monomers. Thus we obtain
(29)
that combine the variables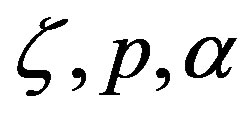
, and
. The significance of Eq.29 may be discerned by displaying the functional dependence between two quantities while keeping the third constant and regarding the fourth as a parameter. For example, solving Eq.29 for α versus the polypeptide length 
we obtain the plots in Figure 3, showing the effect of the catalytic efficiency on the maximum attainable fraction of constrained amino acid units. For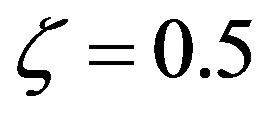 
Eq.29 has solutions with positive 
only for
, a fact that we already determined from the results in Figure 2. Significant values for both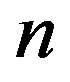 
and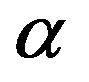 
are only attained with
, but, on the other hand, there is a saturation effect around 
that makes very efficient catalysts unnecessary. Conversely, setting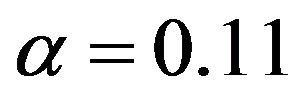 
and
, we can calculate the effect of the size of the amino acid set on the attainable length of the sponta-
neously forming catalytic polypeptides. The curve in Figure 4 shows that a set of amino acids of limited size affords considerably longer polypeptides with respect to chains built from a fairly large set of amino acids. Since the catalytic efficiency of an enzyme requires a large structure, the descending curve of Figure 4 is an indication that the primitive set of amino acids was probably small. The first catalytic polypeptides could have promoted the formation of both a wider range of amino acids and at the same time facilitated peptide bond formation, leading to a self-sustaining cycle in the chemical evolution.
4. CONCLUSIONS
1) The composition of a diluted water mixture of aminoacids in equilibrium with the corresponding polypeptides was computed with respect to the polypeptide length. In the case of a system with an initial concentration c of monomers, the equilibrium concentration of a polypeptide of length n is negligibly small, of the order of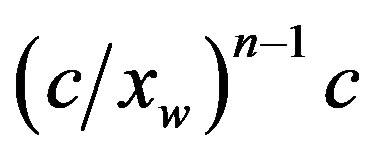
.
2) The equation for the time evolution of a system with a source of amino acids was solved both in the uncatalyzed and catalyzed scenarios, affording the steady state concentration of the polypeptides of length n as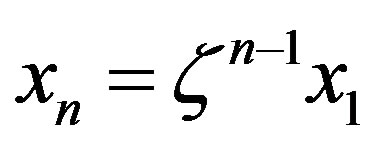
. The different values of the parameter 
in the two cases (
for the uncatalyzed case and 
for the catalyzed case) regulate the concentration.
3) The length of the polypeptides at steady state is also strongly dependent on the value of the parameter
. In the absence of catalysis the maximum length is restricted to a few units, while for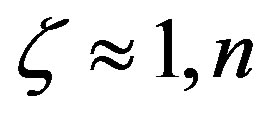 
may reach a few hundred. The model is able to assess the magnitude of the catalytic efficiency required for the formation of a poly-
peptide of a given length.
4) From the intensity of the incoming flux of amino acids on the early Earth from interplanetary dust particles, the constant steady state concentration of amino acid momomers is estimated to be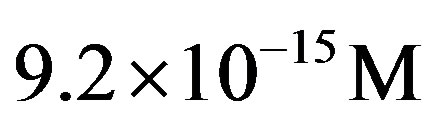 
for the catalyzed scenario. The concentration of a polypeptide of 200 amino acid units is predicted to be only about one order of magnitude less than the steady state concentration of monomers.
5) The effect of the catalytic efficiency on the maximum attainable fraction of conserved residues is estimated to fade around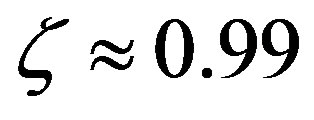
. The maximum attainable length of the polypeptides is a decreasing function of the size of the amino acid set.