1. Introduction and Preliminaries
The Gauss Hypergeometric Function is defined [2] as:
 ; and (1.1)
; and (1.1)
The Generalized Hypergeometric Function, in a classical sense has been defined [3] by
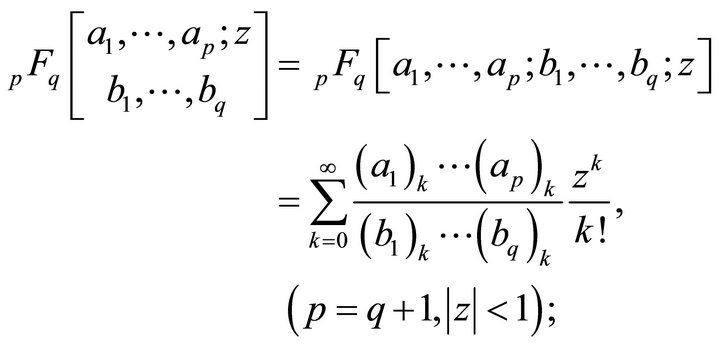 (1.2)
(1.2)
and no denominator parameter equal to zero or negative integer.
E. Wright [4] has further extended the generalization of the hypergeometric series in the following form
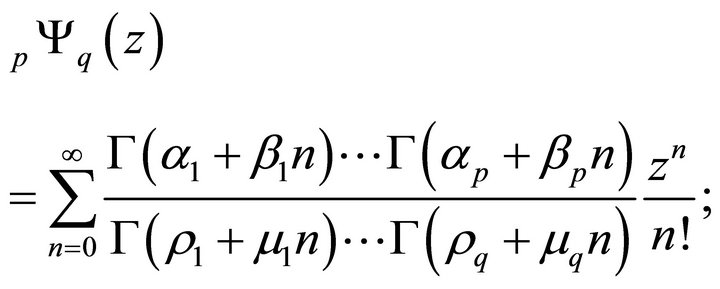 (1.3)
(1.3)
where  and
and  are real positive numbers such that
are real positive numbers such that

When 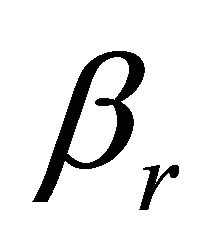 and
and  are equal to 1, Equation (1.3) differs from the generalized hypergeometric function
are equal to 1, Equation (1.3) differs from the generalized hypergeometric function  by a constant multiplier only.
by a constant multiplier only.
The generalized form of the hypergeometric function has been investigated by Dotsenko [5], Malovichko [6] and one of the special cases considered by Dotsenko [5] as
 (1.4)
(1.4)
and its integral representation expressed as
 (1.5)
(1.5)
where . This is the analogue of Euler’s formula for the Gauss’s hypergeometric function [3]. In 2001 Virchenko et al. [1] defined the said Wright Type Hypergeometric Function by taking
. This is the analogue of Euler’s formula for the Gauss’s hypergeometric function [3]. In 2001 Virchenko et al. [1] defined the said Wright Type Hypergeometric Function by taking 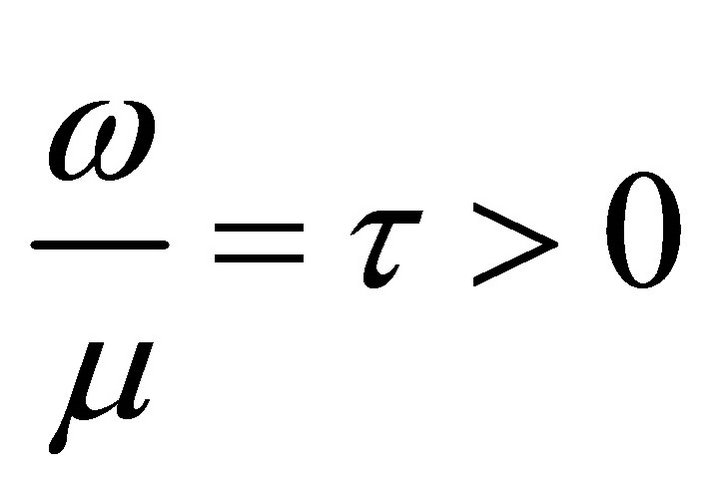 in
in
(1.4) as
 (1.6)
(1.6)
If , then (1.3) reduces to a Gauss’s hypergeometric function. Galue et al. [7] and Virchenko et al. [1] investigated some properties of the function
, then (1.3) reduces to a Gauss’s hypergeometric function. Galue et al. [7] and Virchenko et al. [1] investigated some properties of the function
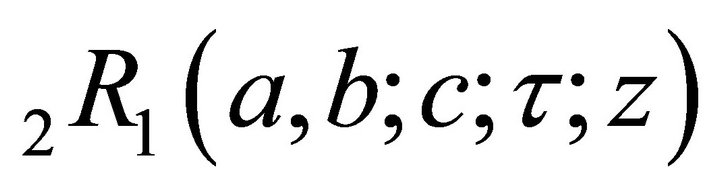 .
.
The following well-known facts have been prepared for studying various properties of the function
 .
.
• Euler (Beta) transform (Sneddon [8]):
The Euler transform of the function 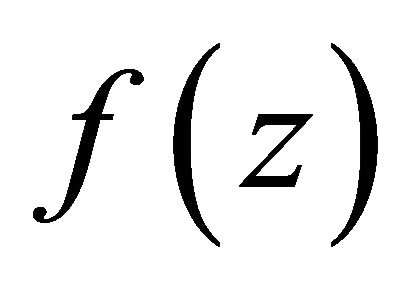 is defined as
is defined as
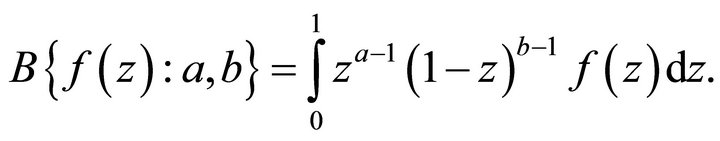 (1.7)
(1.7)
• Laplace transform (Sneddon [8]):
The Laplace transform of the function 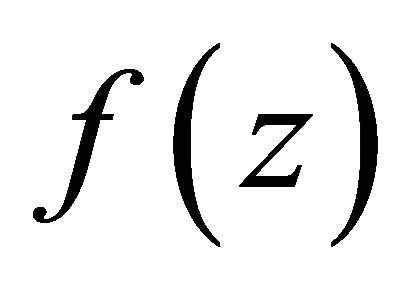 is defined as
is defined as
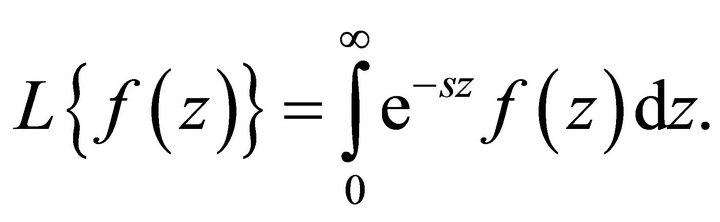 (1.8)
(1.8)
• Mellin transform (Sneddon [8]):
The Mellin transform of the function  is defined as
is defined as
 (1.9)
(1.9)
then
 (1.10)
(1.10)
• Wright generalized hypergeometric function (Srivastava and Manocha [9]), denoted by , is defined as
, is defined as
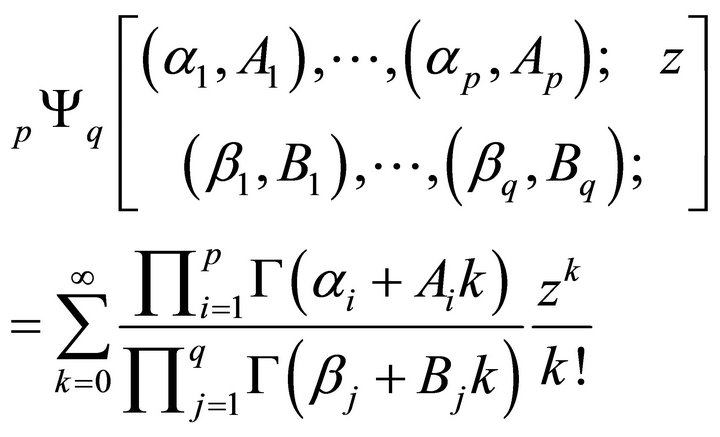 (1.11)
(1.11)
 (1.12)
(1.12)
where 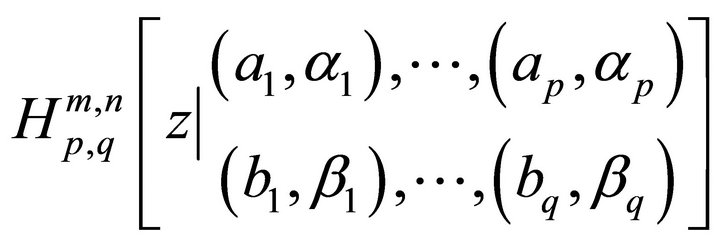 denotes the Fox H-function [10].
denotes the Fox H-function [10].
2. Basic Properties of the Function 
Theorem 2.1
 (2.1.1)
(2.1.1)
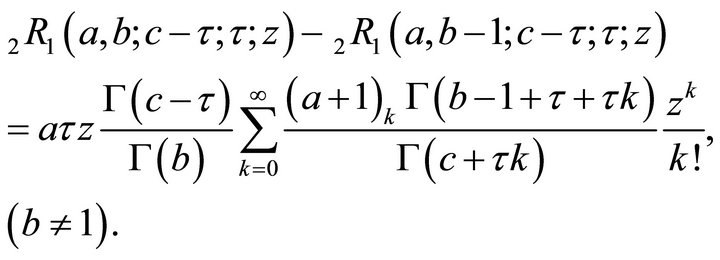 (2.1.2)
(2.1.2)
In particular,
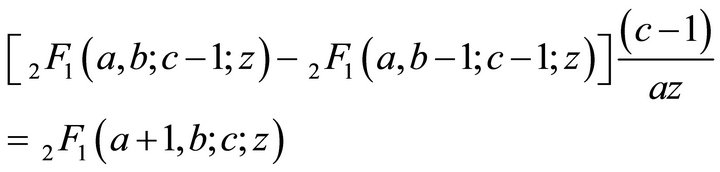 (2.1.3)
(2.1.3)
Proof.
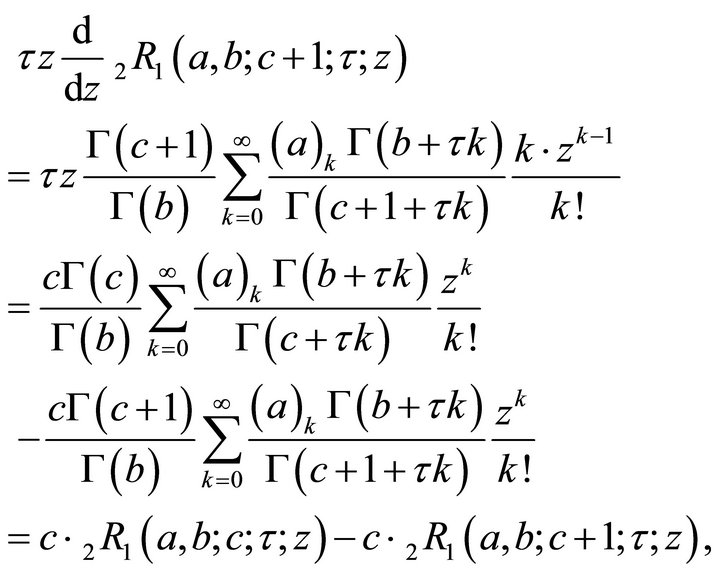
which is the (2.1.1).
Now,
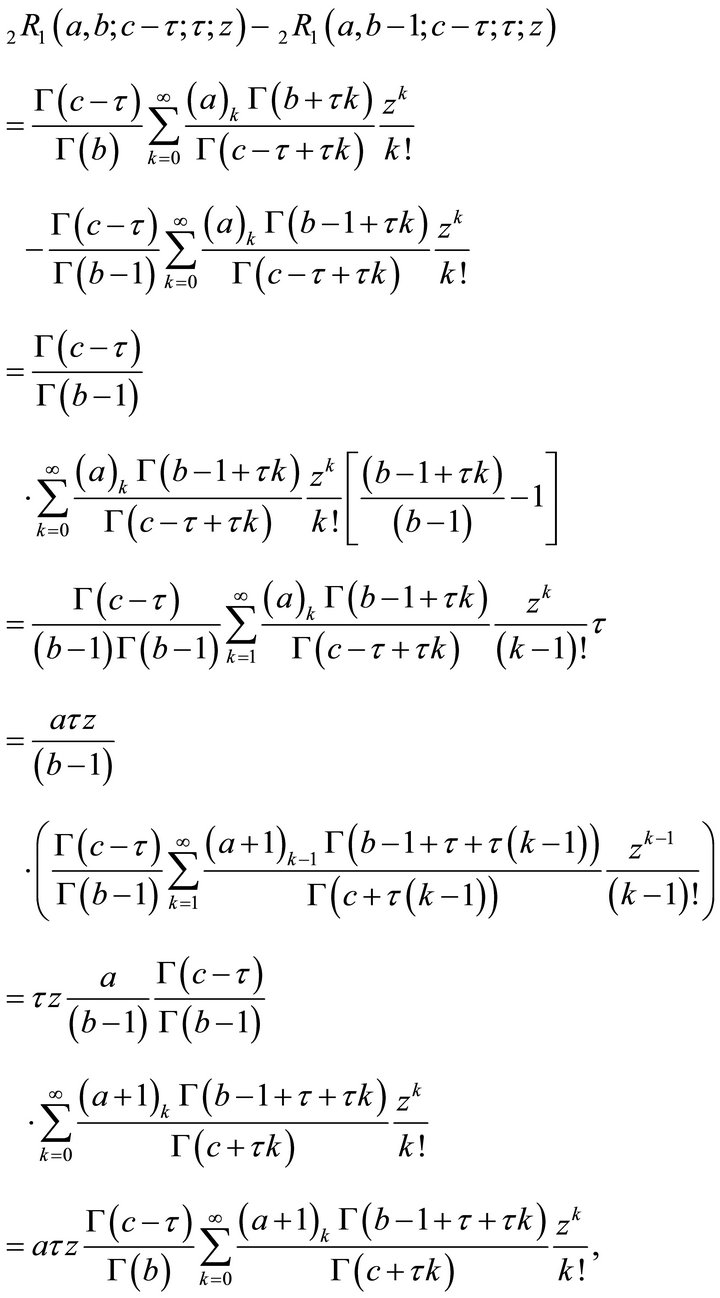
This is the proof of (2.1.2).
For 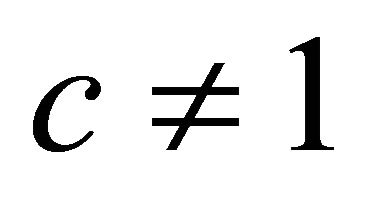 and substituting
and substituting  in above result, this will immediately leads to particular case (2.1.3).
in above result, this will immediately leads to particular case (2.1.3). 
Theorem 2.2 1) If
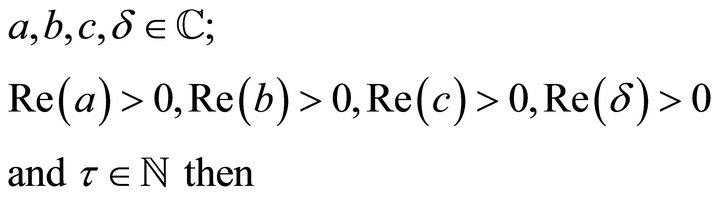
 (2.2.1)
(2.2.1)
2) If
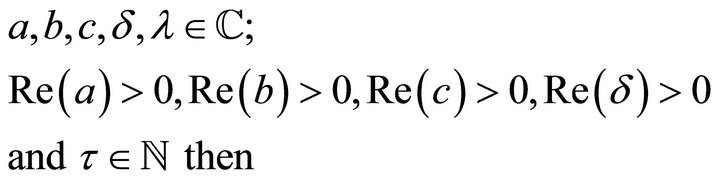
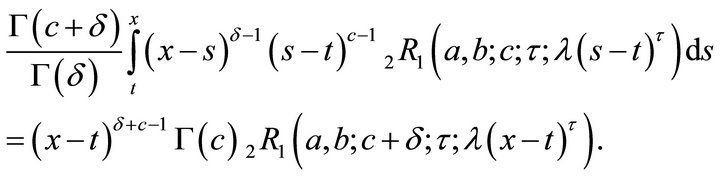
(2.2.2)
3)
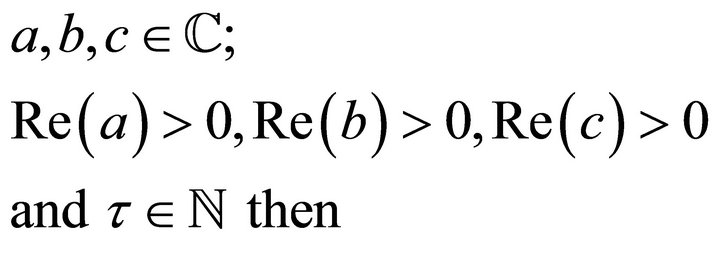
 (2.2.3)
(2.2.3)
In particular,
 (2.2.4)
(2.2.4)
Proof.
1)
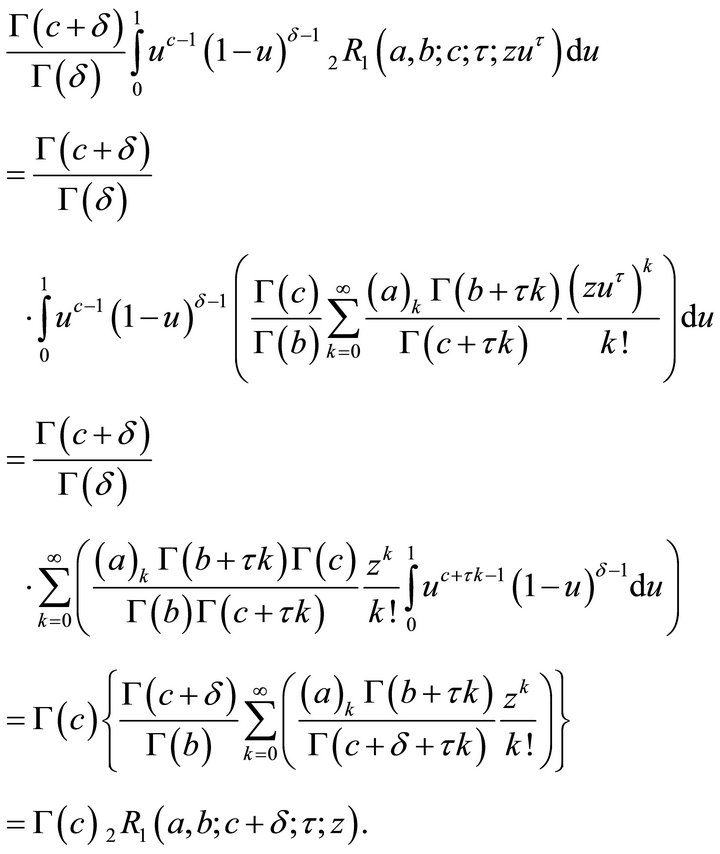
which concludes the proof of (2.2.1). 
2)

Therefore,
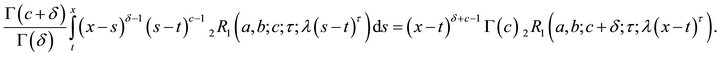
Which is the proof of (2.2.2). 
3)
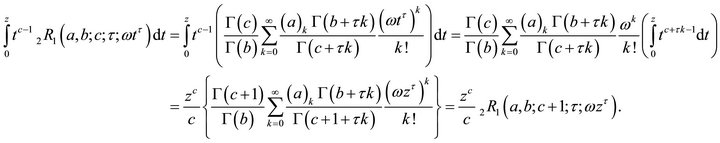
This leads the proof of (2.2.3).
On putting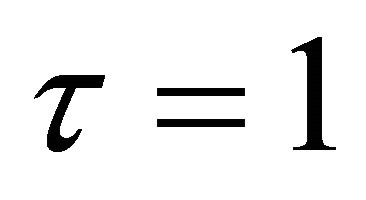 , in the above expression immediately leads to (2.2.4).
, in the above expression immediately leads to (2.2.4). 
Theorem 2.3
If 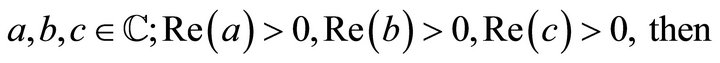
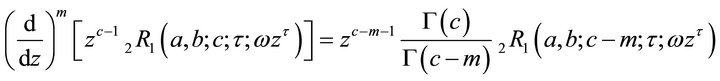 (2.3.1)
(2.3.1)
Proof.

This establishes (2.3.1).
3. Representation of Wright Type
Hypergeometric Function  in Terms of the Function
in Terms of the Function 
Using the definition
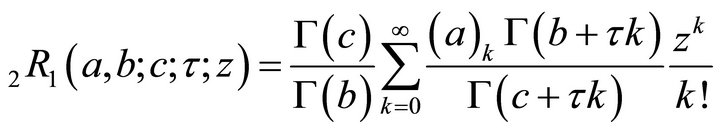 , and taking
, and taking
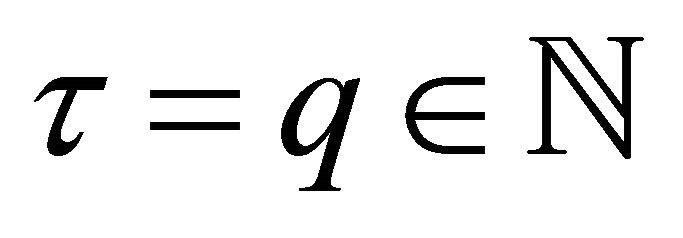 we have
we have
 (3.1)
(3.1)
where 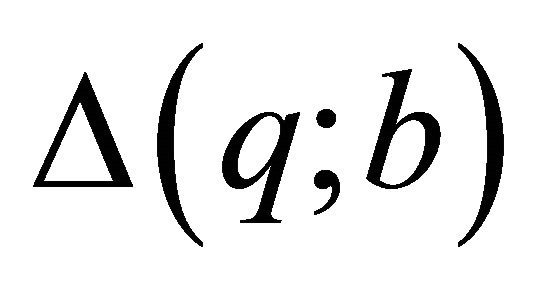 is a
is a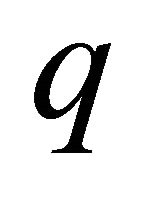 -tuple
-tuple ;
;
 is a
is a 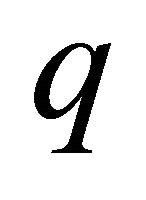 -tuple
-tuple .
.
Convergence criteria for generalized hyperfeometric function
 :
:
1) If , the function
, the function  converges for all finite
converges for all finite .
.
2) If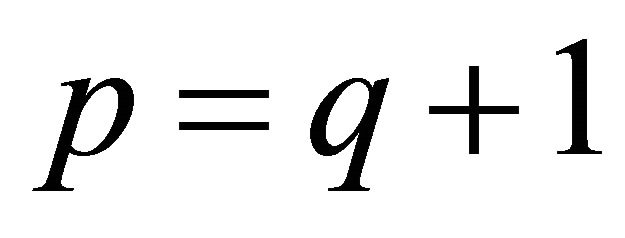 , the function
, the function  converges for
converges for  and diverges for
and diverges for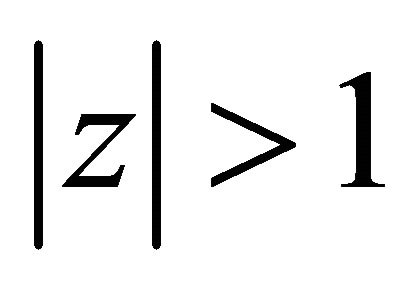 .
.
3) If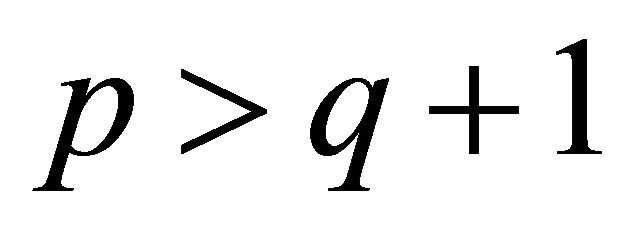 , the function
, the function  is divergent for
is divergent for .
.
4) If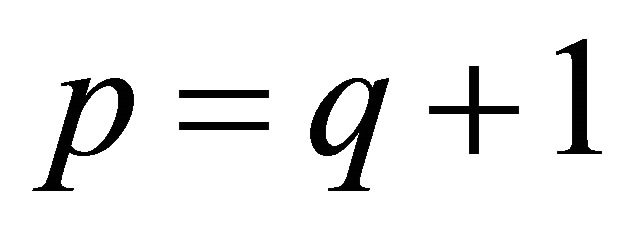 , the function
, the function 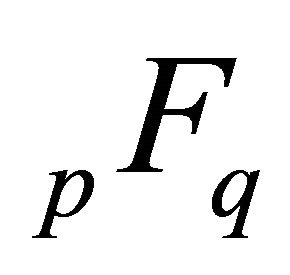 is absolutely convergent on the circle
is absolutely convergent on the circle 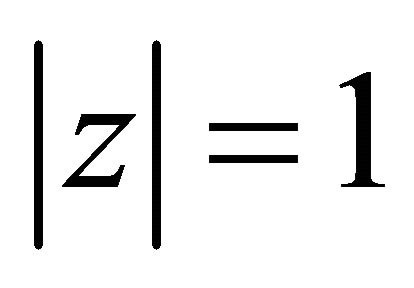 if
if
 .
.
4. Mellin-Barnes Integral Representation of 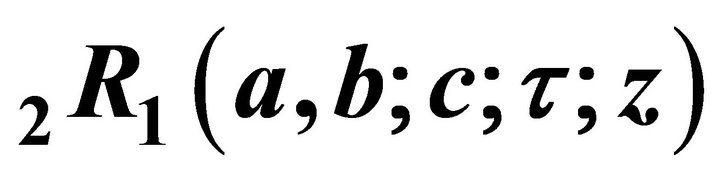
Theorem 4.1 Let
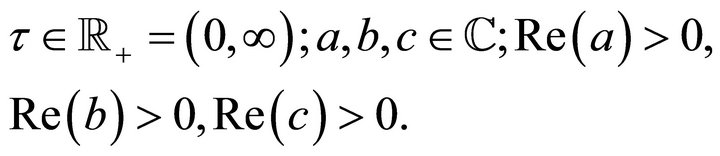
Then  is represented by the MellinBarnes integral
is represented by the MellinBarnes integral
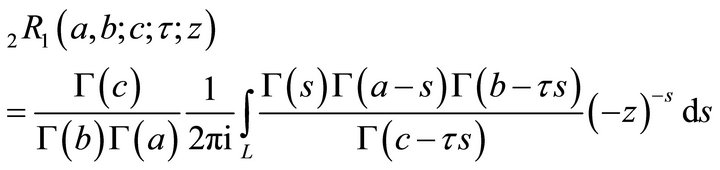
(4.1.1)
where ; the contour of integration beginning at
; the contour of integration beginning at 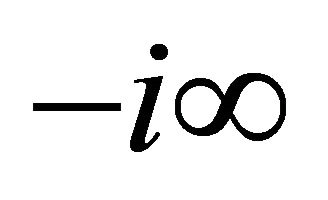 and ending at
and ending at , and intended to separate the poles of the integrand at
, and intended to separate the poles of the integrand at 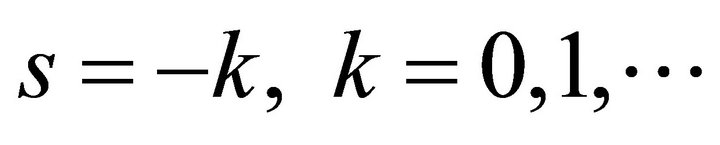 to the left and all the poles at
to the left and all the poles at 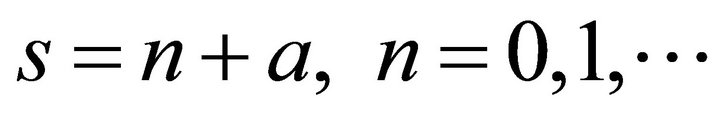 as well as
as well as
 to the right.
to the right.
Proof. We shall use the sum of residues at the poles  to obtain the integral of (4.1.1).
to obtain the integral of (4.1.1).
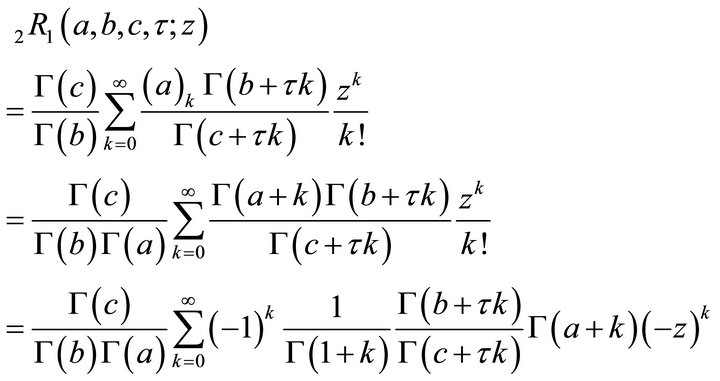
(4.1.2)
Now,
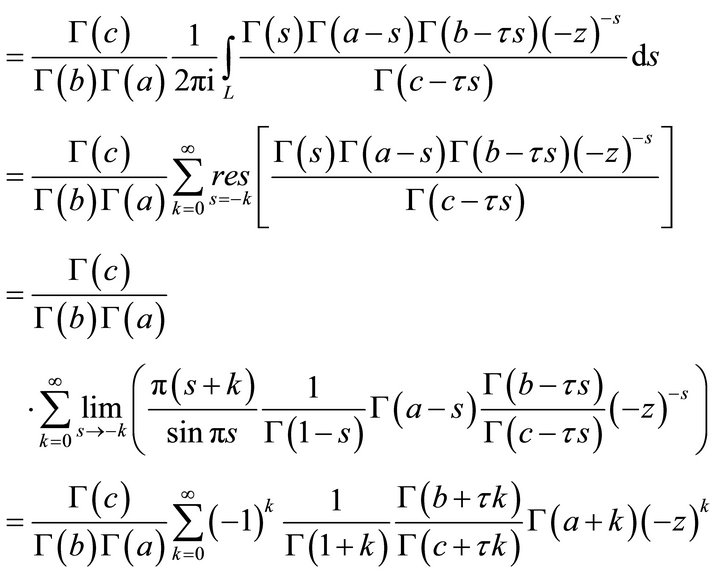
(4.1.3)
(4.1.2) and (4.1.3) completes the proof of (4.1.1). 
5. Integral Transforms of 
In this section we discussed some useful integral transforms like Euler transforms, Laplace transform, Mellin transform and Whittaker transform.
Theorem 5.1 (Euler (Beta) transforms).
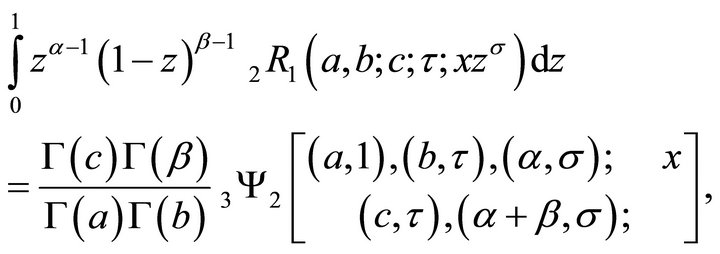 (5.1.1)
(5.1.1)
Proof.
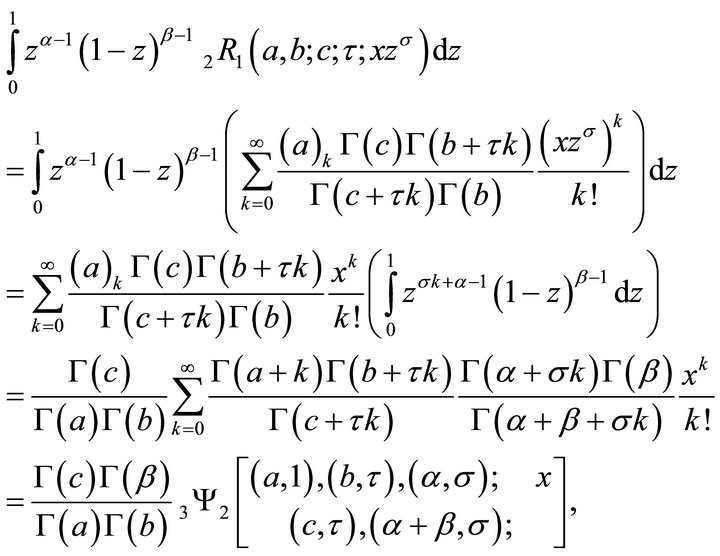
This is the proof of (5.1.1). 
Remark: Putting  in (5.1.1), we get
in (5.1.1), we get
 (5.1.2)
(5.1.2)
Taking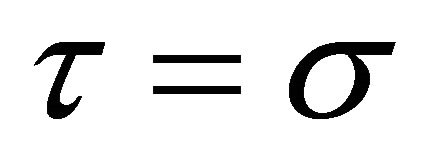 ,
, 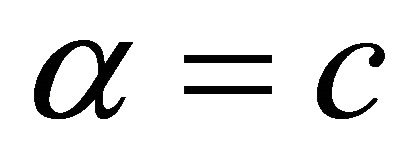 and substituting
and substituting 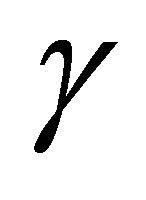 in place of the notation
in place of the notation ; (5.1.1) reduces to
; (5.1.1) reduces to
 (5.1.3)
(5.1.3)
Also, considering  and
and 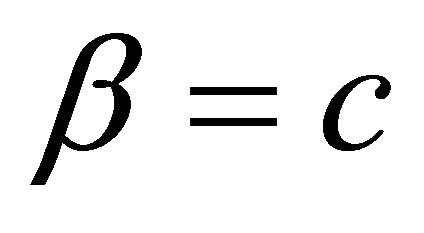 in (5.1.1), with replacement of
in (5.1.1), with replacement of  by
by 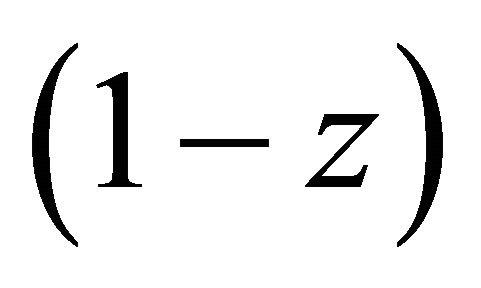 at
at , we get
, we get
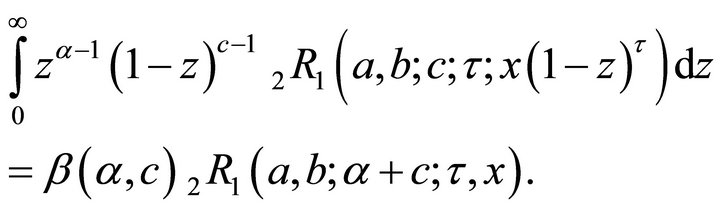 (5.1.4)
(5.1.4)
Theorem 5.2 (Laplace transform).
 (5.2.1)
(5.2.1)

Proof.
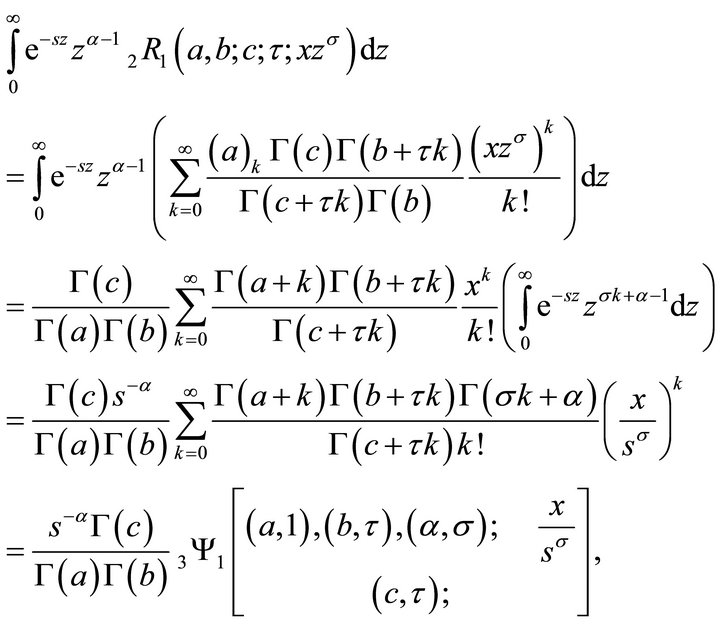
This is the proof of (5.2.1). 
Theorem 5.3 (Mellin transform).
 (5.3.1)
(5.3.1)
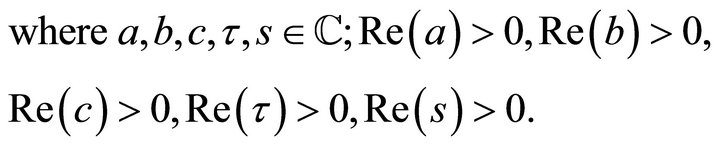
Proof. Putting  in (4.1.1), we get
in (4.1.1), we get
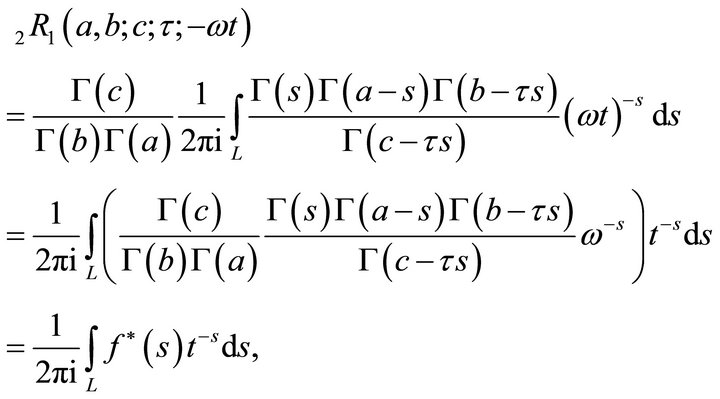
(5.3.2)
where, 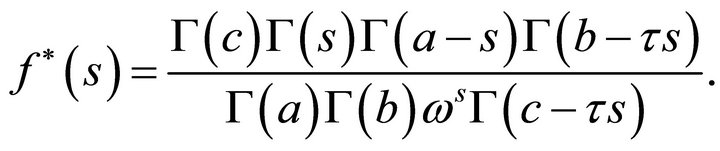
Using (1.9), (1.10), and (5.3.2) immediately lead to (5.3.1). 
Theorem 5.4 (Whittaker transform).
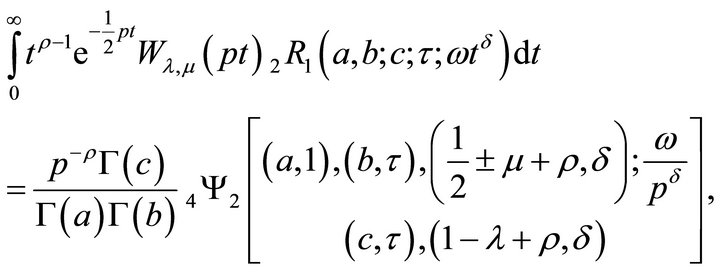
(5.4.1)
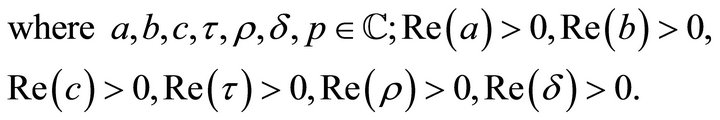
Proof. To obtain Whittaker transform, we use the following integral:
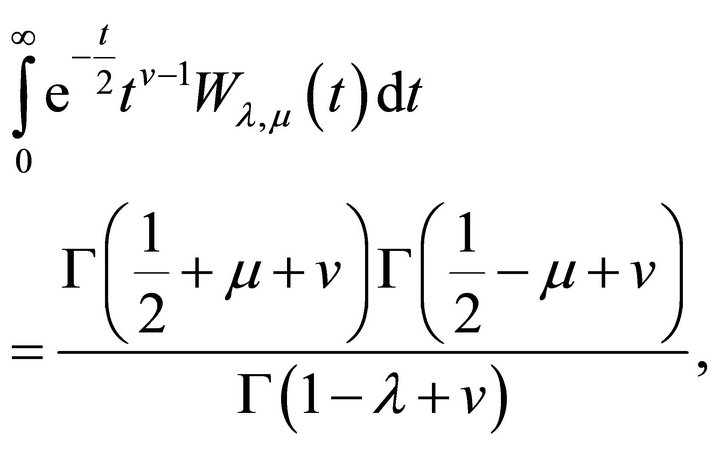
where 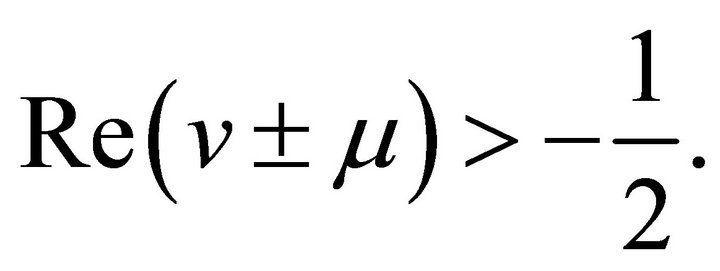
Substituting 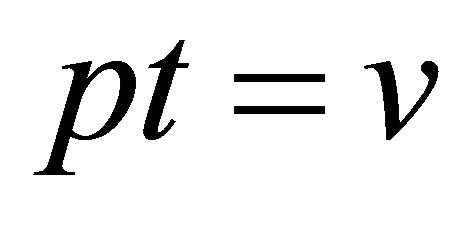 on the L.H.S. of (5.4.1), it reduces to
on the L.H.S. of (5.4.1), it reduces to
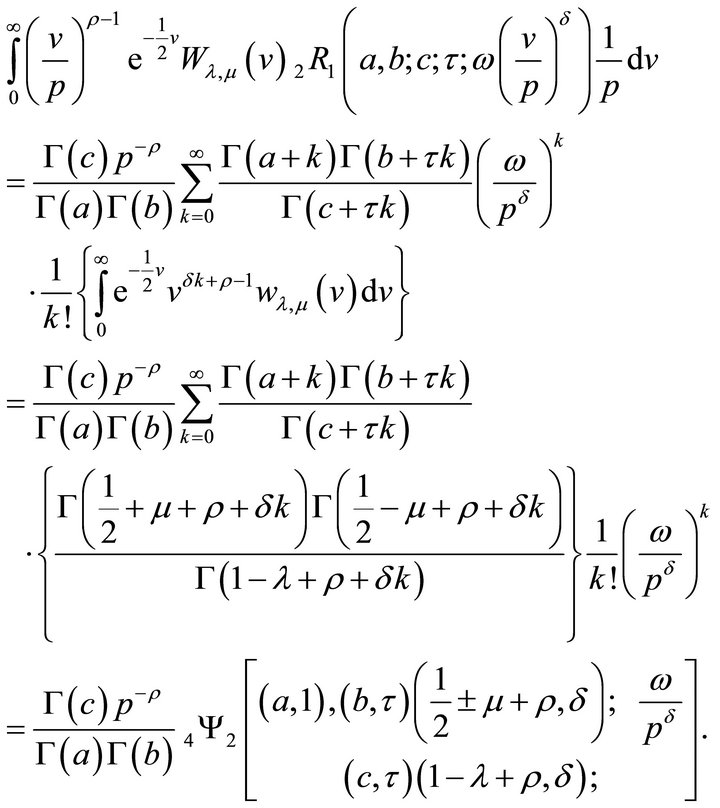
This completes the proof of (5.4.1).
6. Relationship with Some Known Special Functions (Fox H-Function, Wright Hypergeometric Function)
6.1. Relationship with Fox H-Function
Using (4.1.1), we get
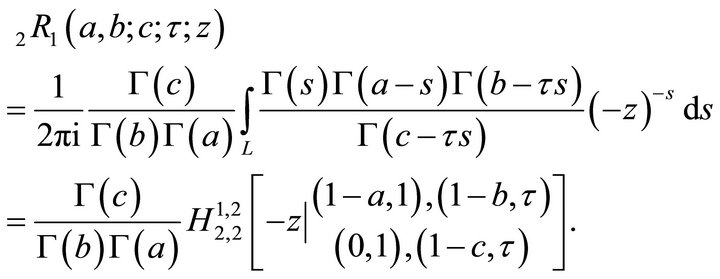
6.2. Relationship with Wright Hypergeometric Function
The Generalized Hypergeometric Function  as in (1.3) is
as in (1.3) is
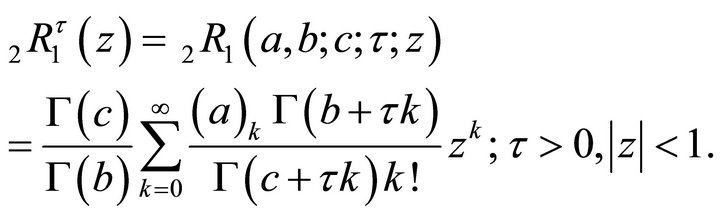 (6.2.1)
(6.2.1)
From (1.11) and (6.2.1) yields
 . (6.2.2)
. (6.2.2)
7. Acknowledgements
The authors are thankful to the reviewers for their valuable suggestions to improve the quality of paper.