Edge Colorings of Planar Graphs without 6-Cycles with Two Chords ()
1. Introduction
All graphs considered here are finite and simple. Let G be a graph with the vertex set 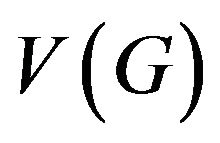 and edge set
and edge set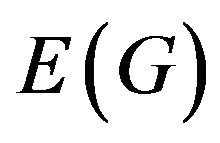 . If
. If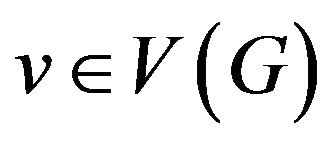 , then its neighbor set
, then its neighbor set 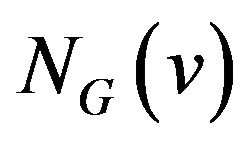 (or simply
(or simply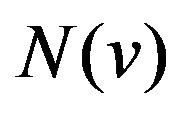 ) is the set of the vertices in G adjacent to v and the degree
) is the set of the vertices in G adjacent to v and the degree 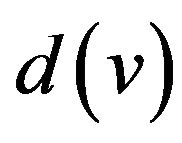 of v is
of v is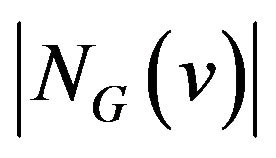 . We denote the maximum degree of
. We denote the maximum degree of  by
by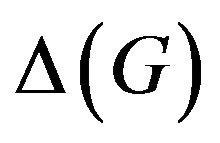 . For
. For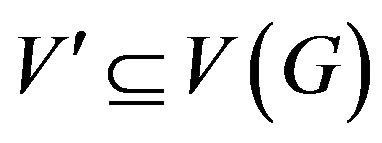 , we denote
, we denote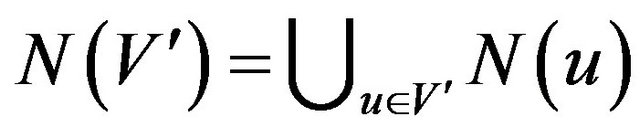 . A
. A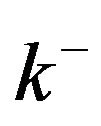 ,
, 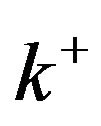 -vertex is a vertex of degree k, at least k. A k (or
-vertex is a vertex of degree k, at least k. A k (or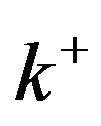 )-vertex adjacent to a vertex x is called a k(or k+)-neighbor of x. Let dk(x), dk+(x) denote the number of k-neighbors, k+-neighbors of x. A k-cycle is a cycle of length k. Two cycles sharing a common edge are said to be adjacent. Given a cycle C of length k in G, an edge
)-vertex adjacent to a vertex x is called a k(or k+)-neighbor of x. Let dk(x), dk+(x) denote the number of k-neighbors, k+-neighbors of x. A k-cycle is a cycle of length k. Two cycles sharing a common edge are said to be adjacent. Given a cycle C of length k in G, an edge 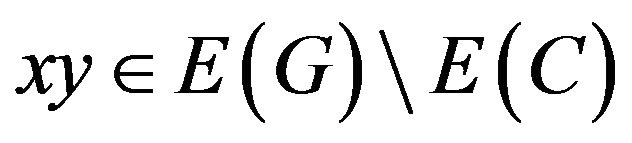 is called a chord of C if
is called a chord of C if 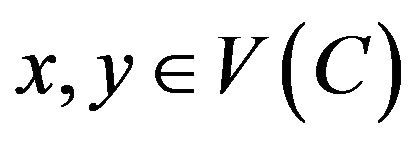 . Such a cycle C is also called a chordalk-cycle.
. Such a cycle C is also called a chordalk-cycle.
A graph is k-edge-colorable, if its edges can be colored with k colors in such a way that adjacent edges receive different colors. The edge chromatic number of a graph G, denoted by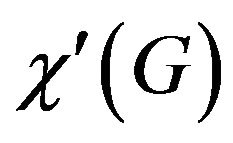 , is the smallest integer k such that G is k-edge-colorable. In 1964, Vizing showed that for every simple graph G,
, is the smallest integer k such that G is k-edge-colorable. In 1964, Vizing showed that for every simple graph G,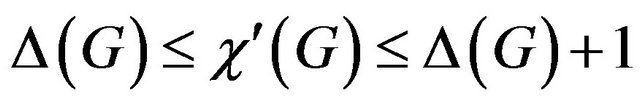 . A graph G is said to be of class 1 if
. A graph G is said to be of class 1 if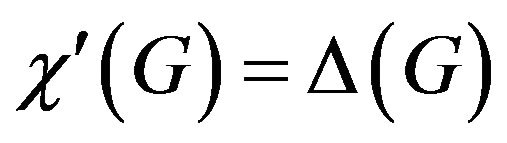 , and of class 2 if
, and of class 2 if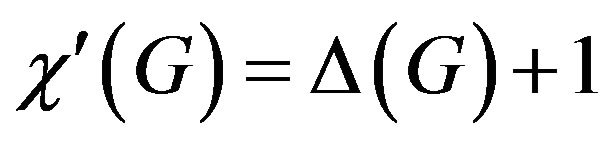 . A graph G is critical if it is connected and of class 2 and
. A graph G is critical if it is connected and of class 2 and 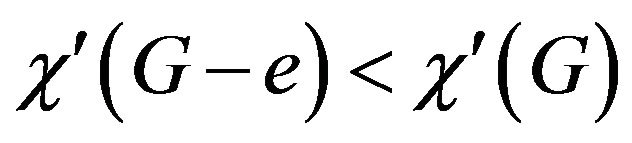 for any edge e of G. A critical graph with maximum degree
for any edge e of G. A critical graph with maximum degree  is called a
is called a  -critical graph. It is clear that every critical graph is 2-connected.
-critical graph. It is clear that every critical graph is 2-connected.
For planar graphs, more is known. As noted by Vizing [1], if C4, K4, the octahedron, and the icosahedron have one edge subdivided each, class 2 planar graphs are produced for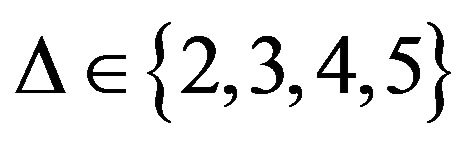 . He proved that every planar graph with
. He proved that every planar graph with 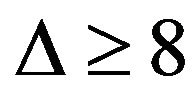 is of class 1 (There are more general results, see [2] and [3]) and then conjectured that every planar graph with maximum degree 6 or 7 is of class 1. The case
is of class 1 (There are more general results, see [2] and [3]) and then conjectured that every planar graph with maximum degree 6 or 7 is of class 1. The case 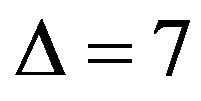 for the conjecture has been verified by Zhang [4] and, independently, by Sanders and Zhao [5]. The case
for the conjecture has been verified by Zhang [4] and, independently, by Sanders and Zhao [5]. The case 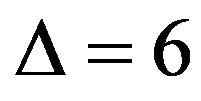 remains open, but some partial results are obtained. Theorem 16.3 in [1] stated that a planar graph with the maximum degree
remains open, but some partial results are obtained. Theorem 16.3 in [1] stated that a planar graph with the maximum degree  and the girth g is of class 1 if
and the girth g is of class 1 if 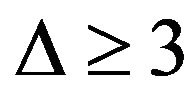 and
and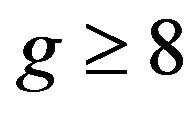 , or
, or  and
and , or
, or 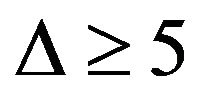 and
and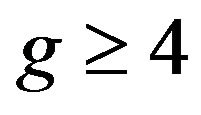 . Lam, Liu, Shiu and Wu [6] proved that a planar graph G is of class 1 if
. Lam, Liu, Shiu and Wu [6] proved that a planar graph G is of class 1 if 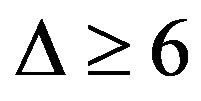 and no two 3-cycles of G sharing a common vertex. Zhou [7] obtained that every planar graph with
and no two 3-cycles of G sharing a common vertex. Zhou [7] obtained that every planar graph with 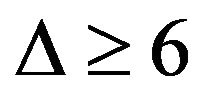 and without 4 or 5-cycles is of class 1. Bu and Wang [8] proved that every planar graph with
and without 4 or 5-cycles is of class 1. Bu and Wang [8] proved that every planar graph with 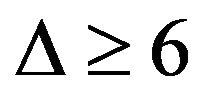 and without 6-cycles is of class 1. Ni [9] extended the result that every planar graph with
and without 6-cycles is of class 1. Ni [9] extended the result that every planar graph with 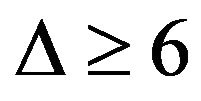 and without chordal 6-cycles is of class 1. In the note, we improve the above result by proving that every planar graph with
and without chordal 6-cycles is of class 1. In the note, we improve the above result by proving that every planar graph with 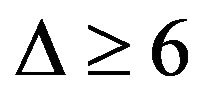 and without 6-cycles with two chords is of class 1.
and without 6-cycles with two chords is of class 1.
2. The Main Result and Its Proof
To prove our result, we will introduce some known lemmas.
Lemma 1. (Vizing’s Adjacency Lemma [1]). Let G be a  -critical graph, and let u and v be adjacent vertices of G with
-critical graph, and let u and v be adjacent vertices of G with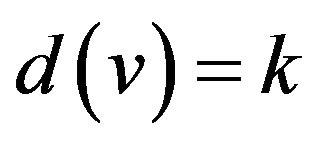 .
.
1) If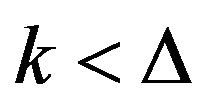 , then u is adjacent to at least
, then u is adjacent to at least 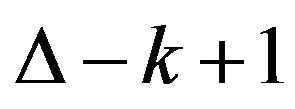 vertices of degree
vertices of degree ;
;
2) If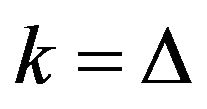 , then u is adjacent to at least two vertices of degree
, then u is adjacent to at least two vertices of degree .
.
From the Vizing’s Adjacency Lemma, it is easy to get the following corollary.
Corollary 2. Let G be a  -critical graph. Then 1) Every vertex is adjacent to at most one 2-vertex and at least two
-critical graph. Then 1) Every vertex is adjacent to at most one 2-vertex and at least two  -vertices;
-vertices;
2) The sum of the degree of any two adjacent vertices is at least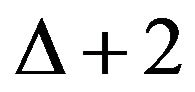 ;
;
3) If 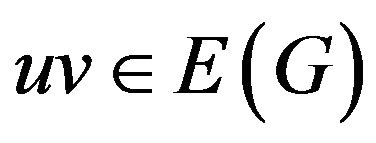 and
and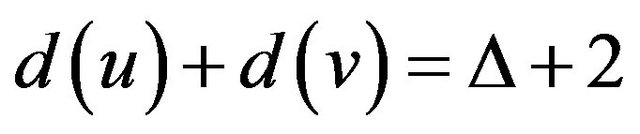 , then every vertex of
, then every vertex of 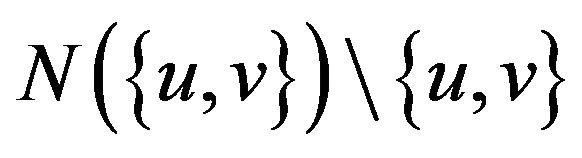 is a
is a -vertex.
-vertex.
Lemma 3 [4]. Let G be a  -critical graph,
-critical graph, 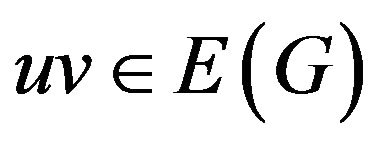 and
and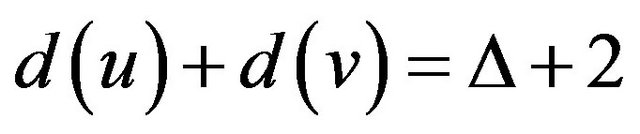 . Then 1) every vertex of
. Then 1) every vertex of  is of degree at least
is of degree at least ;
;
2) if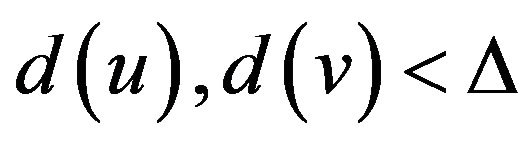 , then every vertex of
, then every vertex of 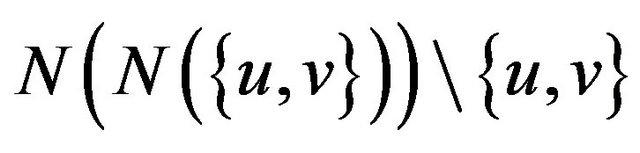 is a
is a  -vertex.
-vertex.
Lemma 4 [5]. No  -critical graph has distinct vertices x, y, z such that x is adjacent to y and z,
-critical graph has distinct vertices x, y, z such that x is adjacent to y and z, 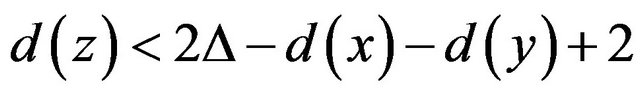 and xz is in at least
and xz is in at least 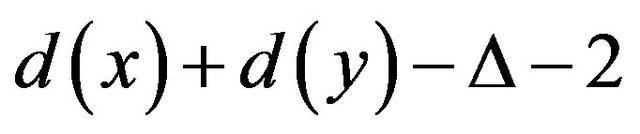 triangles not containing y.
triangles not containing y.
To be convenient, for a plane graph G, let 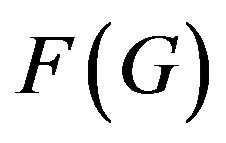 be the face set of G. A face of a graph is said to be incident with all edges and vertices in its boundary. Two faces sharing an edge e are said to be adjacent at e. A degree of a face f, denoted by
be the face set of G. A face of a graph is said to be incident with all edges and vertices in its boundary. Two faces sharing an edge e are said to be adjacent at e. A degree of a face f, denoted by 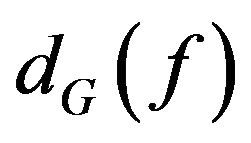 is the number of edges incident with f where each cut edge is counted twice. A k‒, k+-face is a face of degree k, at least k. A k-face of G is denoted by
is the number of edges incident with f where each cut edge is counted twice. A k‒, k+-face is a face of degree k, at least k. A k-face of G is denoted by 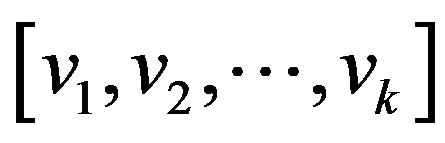 if it is incident with
if it is incident with 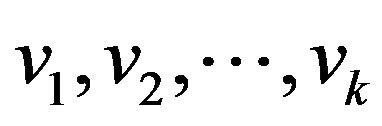 along its boundary. A 3-face
along its boundary. A 3-face 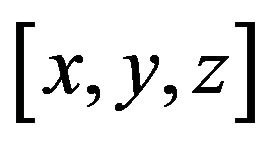 of G is called an
of G is called an 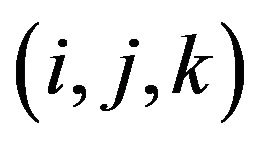 -face if
-face if 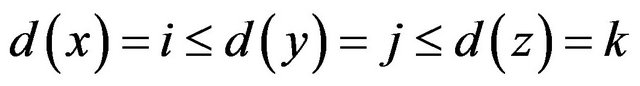 . For a vertex
. For a vertex , we denote by
, we denote by 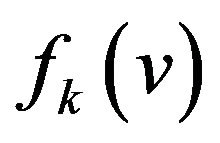 the number of k-faces incident with v.
the number of k-faces incident with v.
Lemma 5 [4,5]. If G is a planar graph with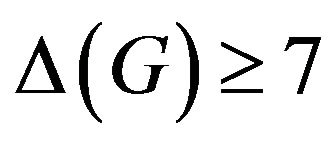 , then G is of class 1.
, then G is of class 1.
Lemma 6 [8]. If G is a graph of class 2, then G contains a k-critical subgraph for each k satisfying 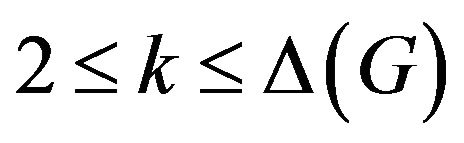 .
.
Theorem 7. Let G be a planar graph with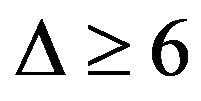 . If any 6-cycle contains at most one chord, then G is of class 1.
. If any 6-cycle contains at most one chord, then G is of class 1.
Proof. Suppose that G is a counterexample to our theorem with the minimum number of edges and suppose that G is embedded in the plane. Then G is a 6-critical graph by Lemmas 5 and 6, and it is 2-connected. By Euler’s formula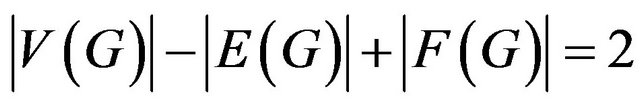 , we have
, we have
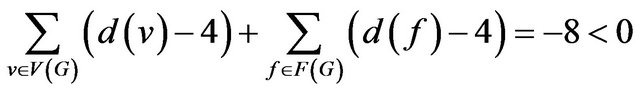
We define ch to be the initial charge. Let
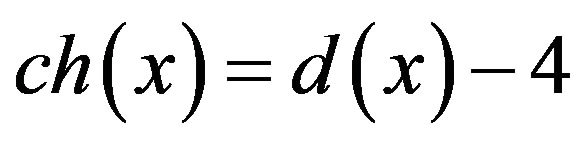 for each
for each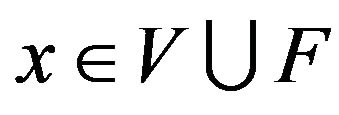 . So
. So 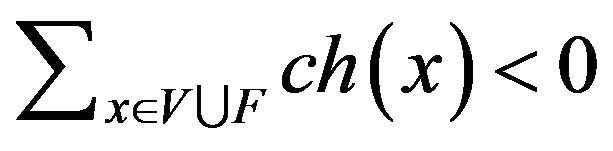 . In the following, we will reassign a new charge denoted by
. In the following, we will reassign a new charge denoted by  to each
to each 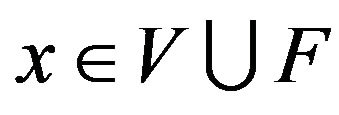 according to the discharging rules. Since our rules only move charges around, and do not affect the sum. If we can show that
according to the discharging rules. Since our rules only move charges around, and do not affect the sum. If we can show that 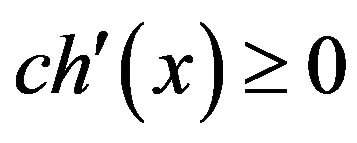 for each
for each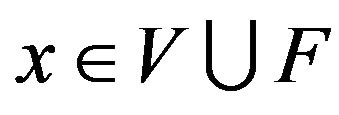 , then we get an obvious contradiction
, then we get an obvious contradiction 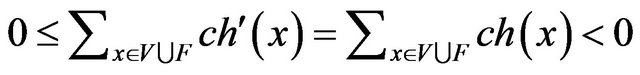 . which completes our proof.
. which completes our proof.
The discharging rules are defined as follows.
R1: Every 5+-face f sends 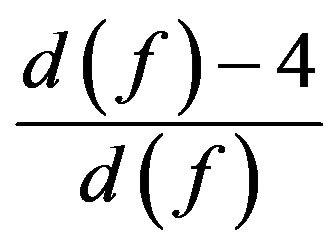 to each incident vertex.
to each incident vertex.
R2: Every 2-vertex receives 1 from each adjacent vertex.
R3: Every 3-vertex receives 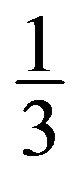 from each adjacent vertex.
from each adjacent vertex.
R4: Let f be a 3-face [x,y,z] with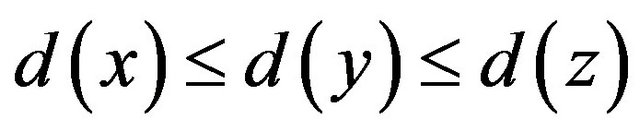 .
.
If 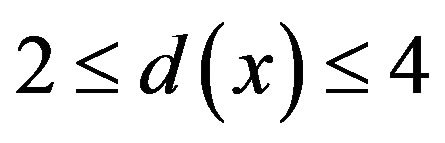 and
and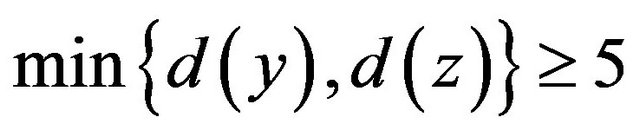 , then f receives
, then f receives 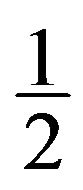 from y,
from y, 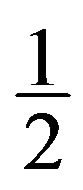 from z; If
from z; If 
and 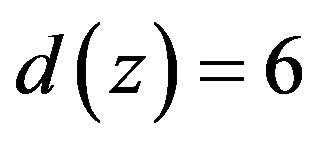 then z sends 1 to f; If
then z sends 1 to f; If
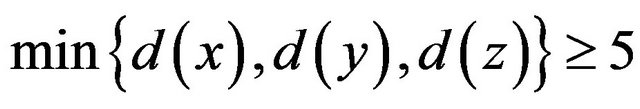 , then x, y, z sends
, then x, y, z sends 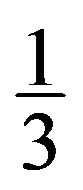 to frespectively.
to frespectively.
R5: If a 5-vertex v is adjacent to a 6-vertex x and incident with a (3,5,6)-face [u,v,w] such that 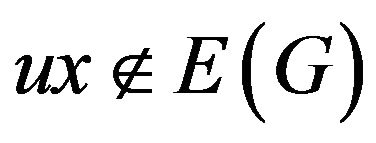
and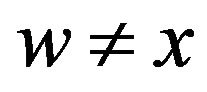 , then x sends
, then x sends 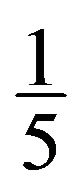 to v.
to v.
Now, let’s began to check 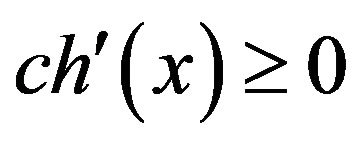 for all
for all
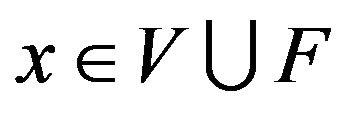 . Let
. Let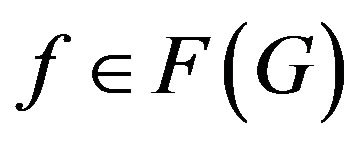 . Then
. Then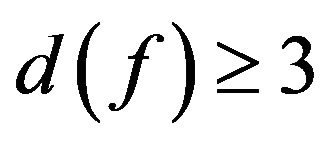 . If
. If
 , then
, then 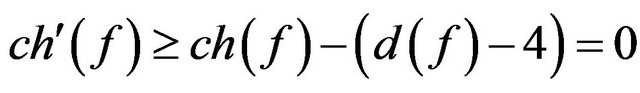 by R1. If
by R1. If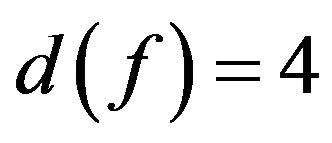 , then
, then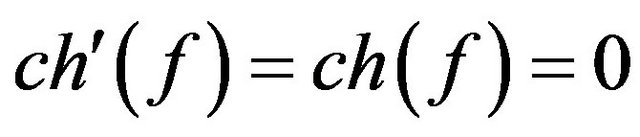 . If
. If then
then  by R4.
by R4.
Let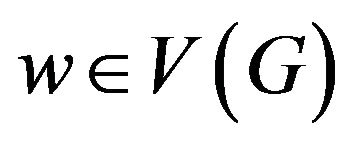 . Then
. Then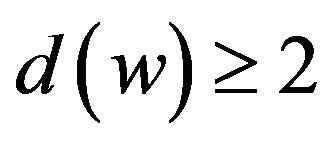 . If
. If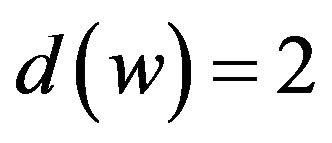 , then
, then
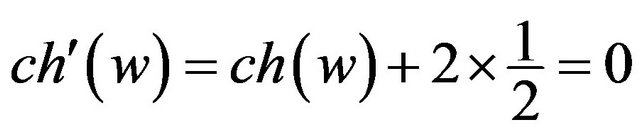 by R2. If
by R2. If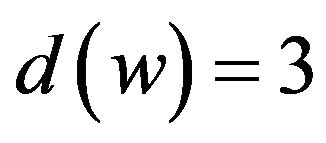 , then w is adjacent to three 5+-vertices by Corollary 2, and it follows that
, then w is adjacent to three 5+-vertices by Corollary 2, and it follows that 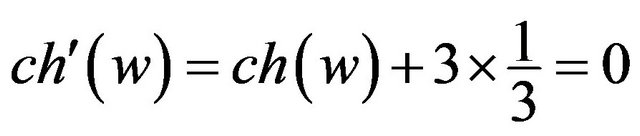 by R3. If
by R3. If
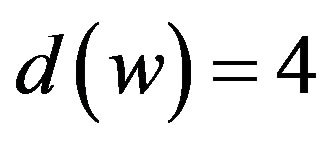 , then
, then .
.
Since any 6-cycle of G contains at most one chord, we have the following claim.
Claim 1. Let f, f', f'' be three faces incident with w such that f' is adjacent to f and f''. If f and f'' are 3-faces, then f' must be a 5+-face.
Suppose that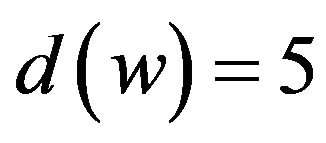 . We have
. We have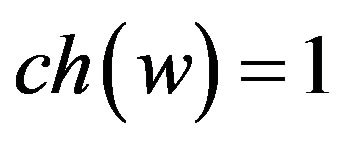 ,
,
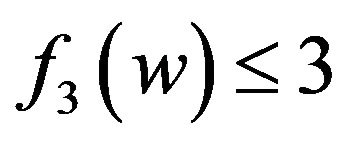 ,
,  ,
, 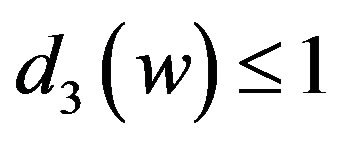 and
and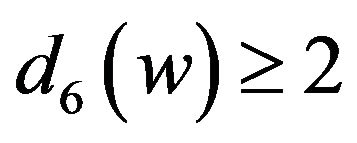 . Let
. Let 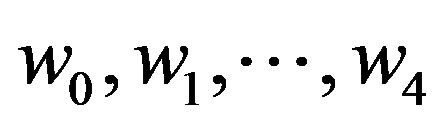 be neighbors of w and
be neighbors of w and 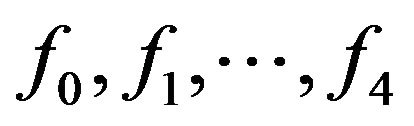 be faces incident with w such that
be faces incident with w such that 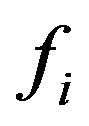 is incident with
is incident with  and
and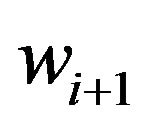 , for all
, for all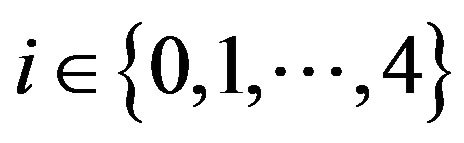 , where
, where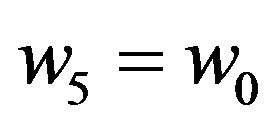 . If all neighbors of w are 5+-vertices, then
. If all neighbors of w are 5+-vertices, then
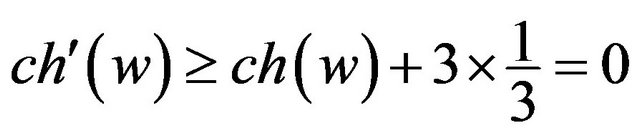 by R4. Suppose that
by R4. Suppose that
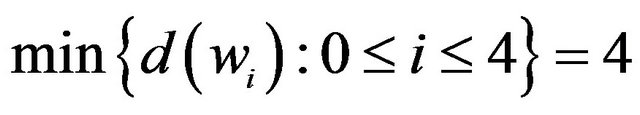 . If
. If , then
, then
 by R4; Otherwise, without loss of generality, assume that
by R4; Otherwise, without loss of generality, assume that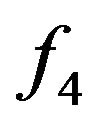 ,
, 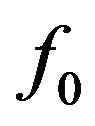 ,
, 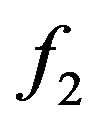 are 3-faces. Then
are 3-faces. Then 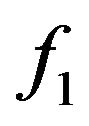 and
and  are 5+-faces by Claim 1. By Lemma 4,
are 5+-faces by Claim 1. By Lemma 4,
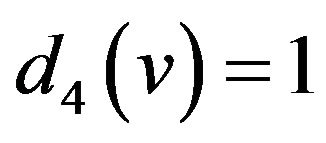 . So
. So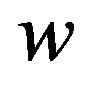 sends at most
sends at most 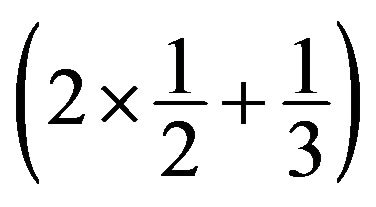 to its adjacent 3-faces. At the same time,
to its adjacent 3-faces. At the same time, 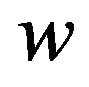 receives at least
receives at least
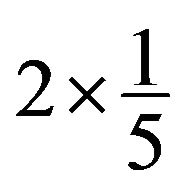 from
from 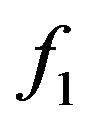 and
and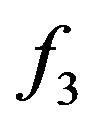 by R1, and it follows that
by R1, and it follows that
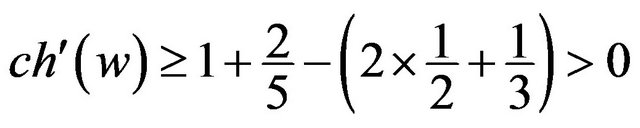 . Suppose that
. Suppose that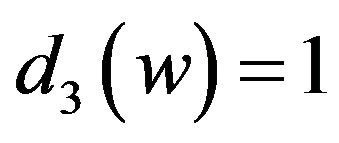 without loss of generality, assume that
without loss of generality, assume that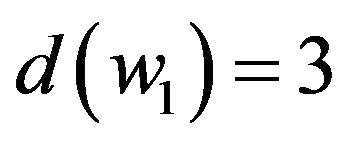 . Then
. Then 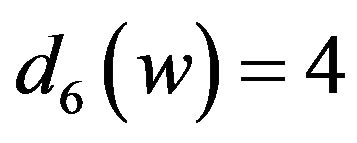 by Lemma 1. If
by Lemma 1. If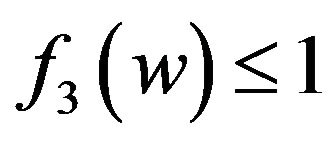 , or
, or 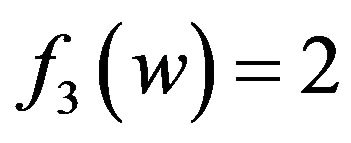 and
and  is not incident with a 3-face, then
is not incident with a 3-face, then
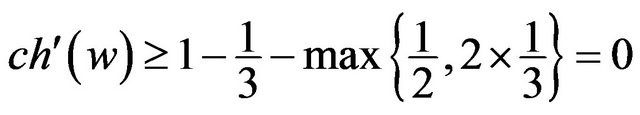 by R3 and R4; Otherwise,
by R3 and R4; Otherwise, 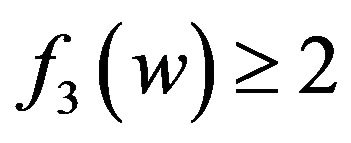 and then
and then  is incident with a 5+- face. If
is incident with a 5+- face. If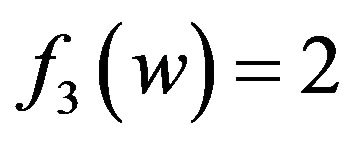 , then
, then
 ; Otherwise,
; Otherwise, 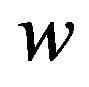 is incident with two 5+-faces. If
is incident with two 5+-faces. If 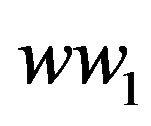 is not incident with a 3face, then
is not incident with a 3face, then 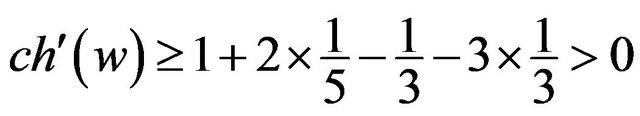 by R3 and R4;
by R3 and R4;
Otherwise, w receives at least  from its neighbors by R5, and it follows that
from its neighbors by R5, and it follows that
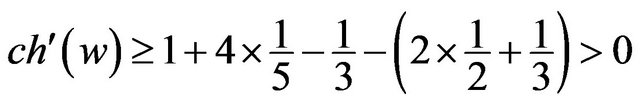 .
.
In the following we check the case that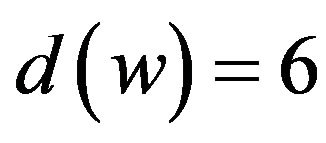 . Thus we have
. Thus we have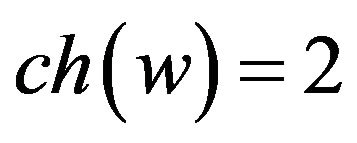 ,
, 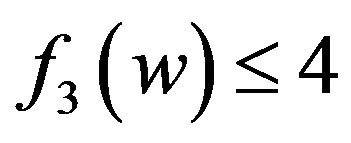 ,
,  and
and 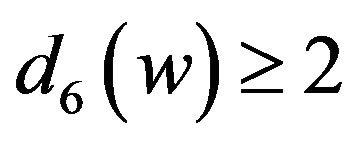 by Lemma 1.
by Lemma 1.
Case 1. w sends positive charge to some adjacent 5-vertex v (ref. R5).
Suppose that v is incident with a (3,5,6)-face [u,v,x] such that 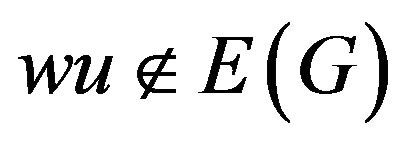 and
and  (see R5). Then
(see R5). Then 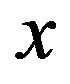
may sends  to
to 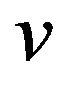 by R5. At the same time,
by R5. At the same time, 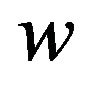 is adjacent to five 6-vertices by Lemma 3, that is,
is adjacent to five 6-vertices by Lemma 3, that is,
 . Since
. Since ,
,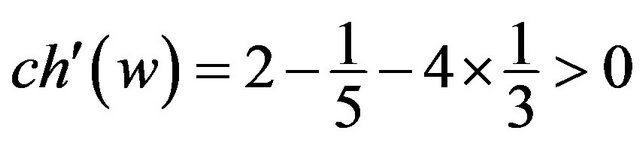 .
.
Case 2.  sends no charge to its adjacent 5+-vertices.
sends no charge to its adjacent 5+-vertices.
Let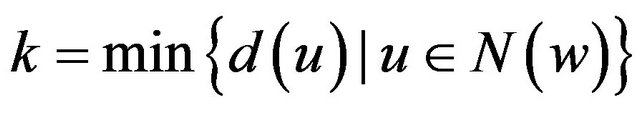 . If
. If , then
, then
 . Suppose that
. Suppose that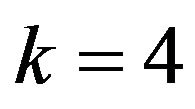 . Then
. Then
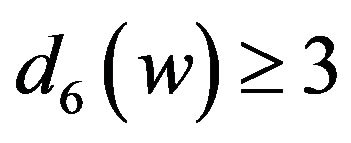 by Lemma 1 and
by Lemma 1 and 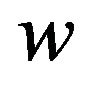 may be incident with a (4,4,6)-face. If
may be incident with a (4,4,6)-face. If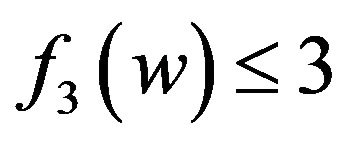 , then
, then
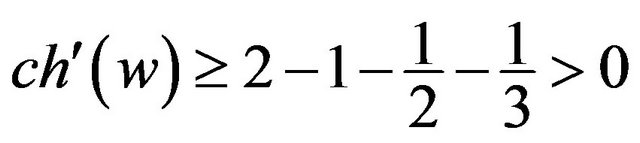 ; Otherwise,
; Otherwise, 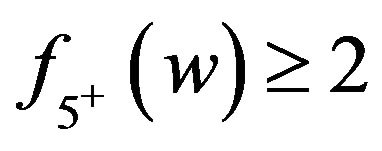 and it follows that
and it follows that
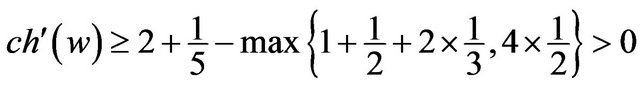 .
.
Suppose that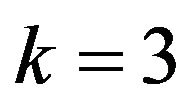 . Then
. Then 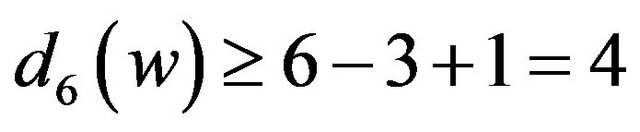 by Lemma 1. If
by Lemma 1. If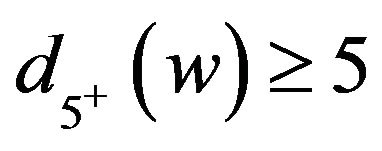 , then
, then
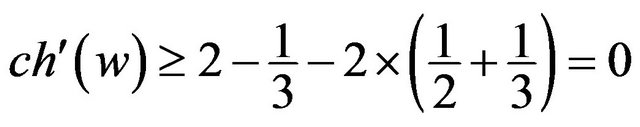 ; Otherwise,
; Otherwise,  is incident with two 4-vertices
is incident with two 4-vertices  then
then 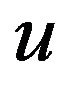 and
and 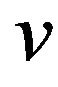 are incident with at most one 3-face by Lemma 4 since
are incident with at most one 3-face by Lemma 4 since . So
. So 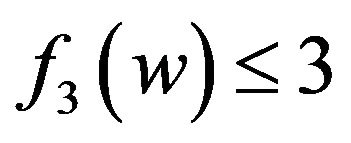 and it follows that
and it follows that 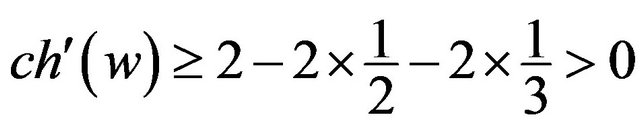 by R3 and R4.
by R3 and R4.
Suppose that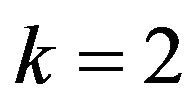 , that is, w is adjacent to a 2-vertex v. Then
, that is, w is adjacent to a 2-vertex v. Then 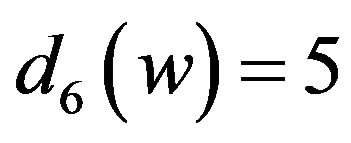 by Lemma 1. If
by Lemma 1. If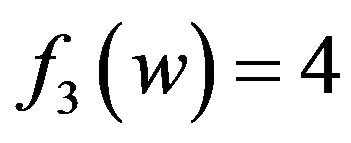 , then
, then 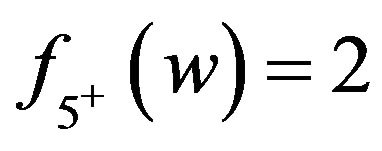 and it follows that
and it follows that
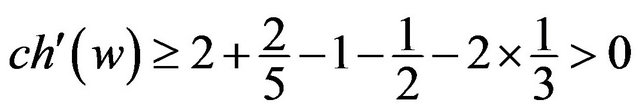 ; Otherwise,
; Otherwise,
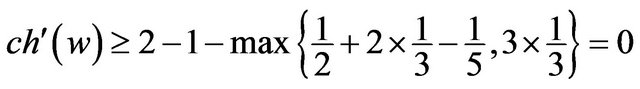 .
.
NOTES