1. Introduction
The celebrated Gnedenko-Raikov theorem states that sums of independent, infinitesimal random variables are asymptotically normal if and only if the sum of squares, centered at truncated means, is relatively stable. The following variant for i.i.d. random variables has been recently proved in [1]:
Theorem 1. Let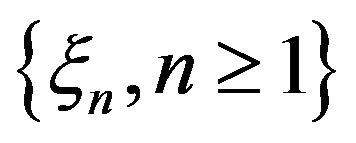 
be i.i.d. random variables with mean zero, and 
a sequence of positive reals increasing to
. Then
if and only if
A classical extension of independence is exchangeability, and in this context we shall prove that the Gnedenko-Raikov theorem fails. First, let us recall the basic facts. A sequence of random variables 
on the probability space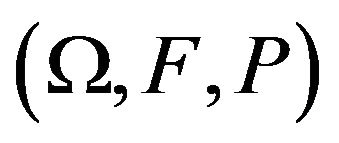 
is said to be exchangeable if for each n,
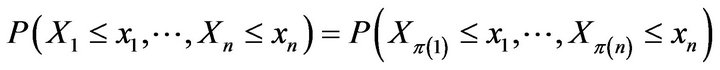
for any permutation π of 
and any
. Two trivial examples are i.i.d. random variables and totally determined random variables 
. Two nontrivial but simple examples are
and 
where the rn’s are i.i.d. and independent of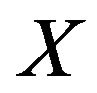 
or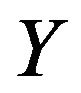
, respectively.
By de Finetti’s theorem, an infinite sequence of exchangeable random variables is conditionally i.i.d. given either the tail 
-field of 
or the 
-field G of permutable events. Furthermore, there exists a regular conditional distribution 
for 
given G such that for each 
the coordinate random variables
, called mixands, of the probability space 
are i.i.d. Namely, for each natural number n, any Borel function
, and any Borel set 
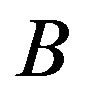on
,
(1)
The following central limit theorem for exchangeable sequences has been proved in [2]:
Theorem 2. Let 
be a sequence of exchangeable random variables. Then there exist constants 
with
, such that
in distribution if and only if there exists a positive sequence 
such that
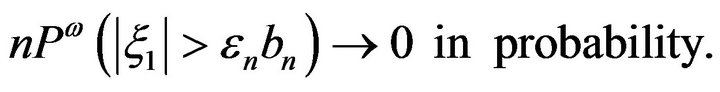
and either 
is slowly varying with
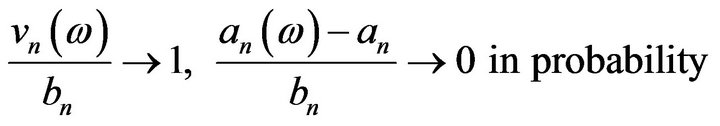
or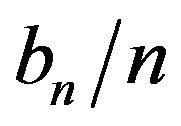 
is slowly varying with
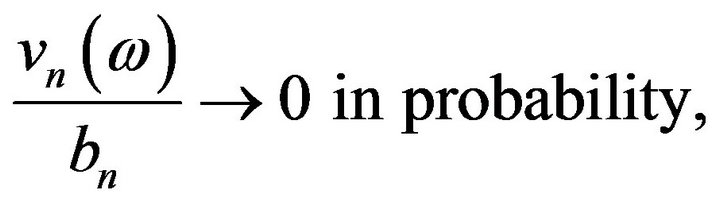
where
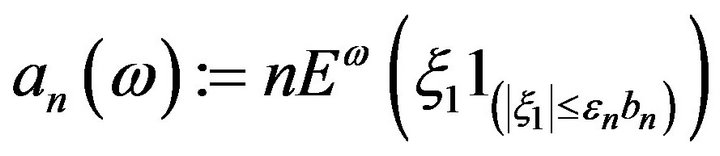
and
In the above theorem, the case where 
is slowly varying characterizes the situation when the classical central limit theorem holds for the mixands, whereas the case where 
is slowly varying characterizes the situation when the law of large numbers holds for the mixands and those limits have a standard normal distribution. Recently, we “cleaned” the latest statement and proved in [3] the following variant of the law of large numbers for exchangeable sequences:
Theorem 3. Let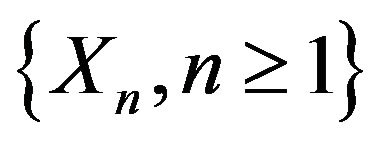 
be a sequence of exchangeable random variables and 
a sequence of positive reals increasing to
, that satisfy the following conditions:
and
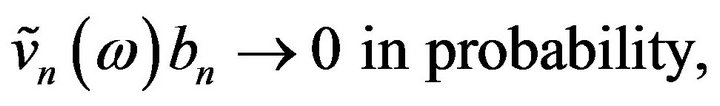
where
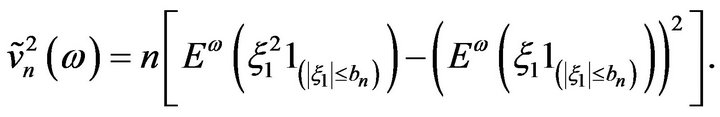
Then
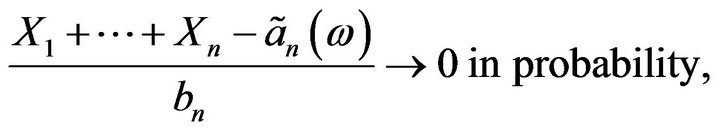
where
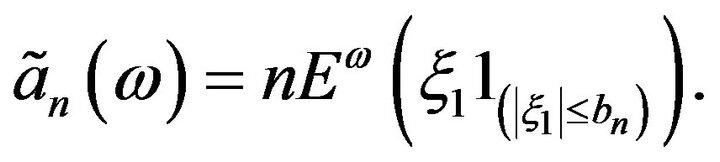
Unless the sequence 
is i.i.d., the converse in the above theorem is not true; more is needed, see [4].
We are now ready to provide the counterexample mentioned in the introduction. It will rely on both Theorems 2 and 3, and some specific constants
. More precisely, we have:
Theorem 4. Let 
be a sequence of exchangeable random variables and 
a sequence of norming constants that satisfy the following condition:
(2)
where 
is the sequence appearing in Theorem 2.
1) Assume that the sequence 
is nondecreasing for some 
and satisfies
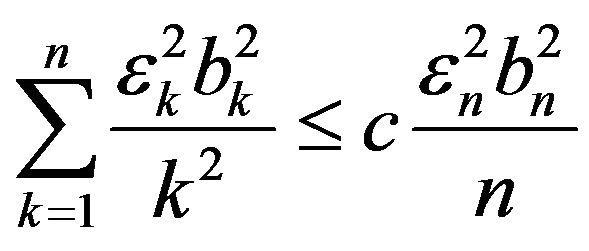
for all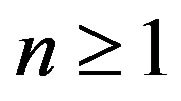 
and some constant
. Then
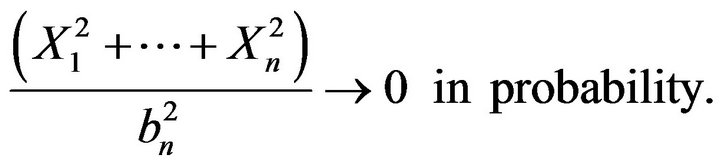
2) If 
and 
are slowly varying for some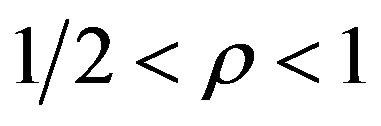
, then
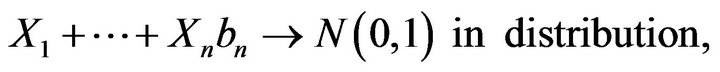
and the Gnedenko-Raikov theorem fails in this case.
Proof of Theorem 4. 1) Under the assumptions on the sequence 
and according to [5], p. 680, we have that
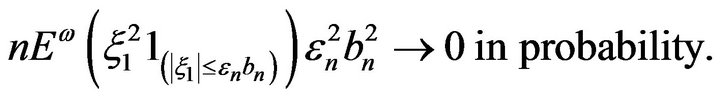
Also, cf. Section 2 in [5], we have that 
and
. These facts imply that
(3)
Taking into account the following identity (with the notations in Theorem 2):
which gives
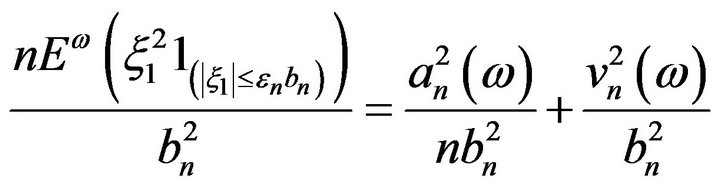
from formula (3) it follows that
(4)
Now let 
be given. By formula (1) and the triangle inequality we have
(5)
Using (2), we estimate the first term in the right hand side of (5) as follows:
(6)
We then break down the second term in the right hand side of (5) as follows:
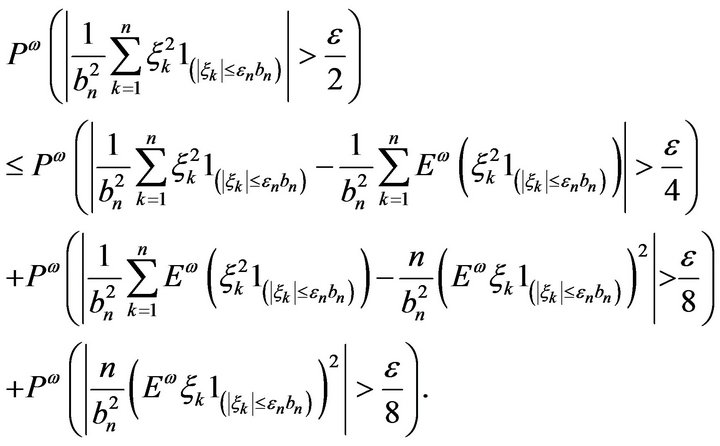
(7)
Using (4), we have
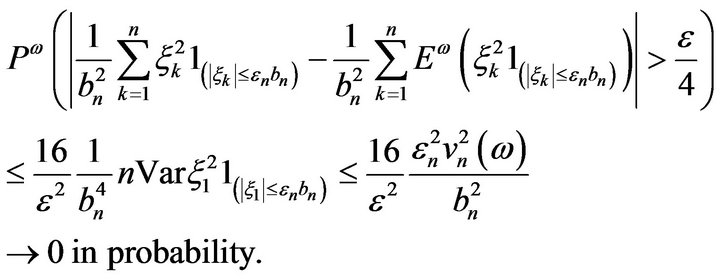
(8)
Also, cf. (4),
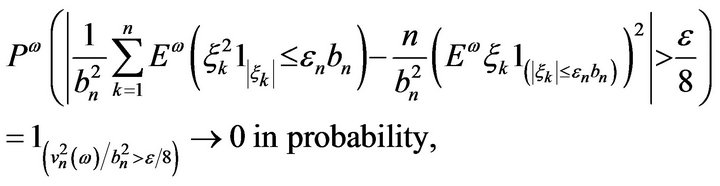
(9)
and, again cf. (4),
(10)
From (5)-(10) we deduce that
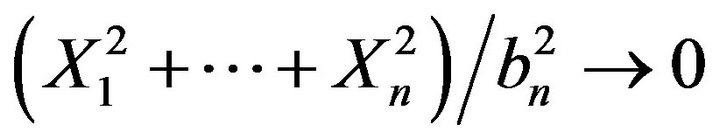in probability.
Now, let us prove 2). If 
is slowly varying, and using (4), Theorems 2 and 3 imply that 
in distribution. If, in addition, 
is slowly varying for some
, then the hypotheses on the sequence 
in part 1) of Theorem 4 are satisfied cf. section 2 in [5], hence the Gnedenko-Raikov theorem fails in this case. □
Remark. It is worth noting that the Gnedenko-Raikov theorem is valid in the case where 
is slowly varying in Theorem 2, as well as in both self-normalized central limit theorem [6] and self-normalized law of large numbers [7] for exchangeable sequences. This is why the counterexample in Theorem 4 above was rather hard to get.
The research of George Stoica and Deli Li was partially supported by grants from the Natural Sciences and Engineering Research Council of Canada.
NOTES