Applications of Multivalent Functions Associated with Generalized Fractional Integral Operator ()
1. Introduction
Let  denote the class of functions
denote the class of functions 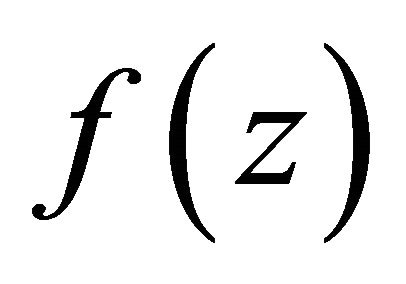 of the form
of the form
 (1.1)
(1.1)
which are analytic in the open unit disk  Also let f and g be analytic in
Also let f and g be analytic in  with
with . Then we say that f is subordinate to g in
. Then we say that f is subordinate to g in , written
, written  or
or , if there exists the Schwarz function w, analytic in
, if there exists the Schwarz function w, analytic in  such that
such that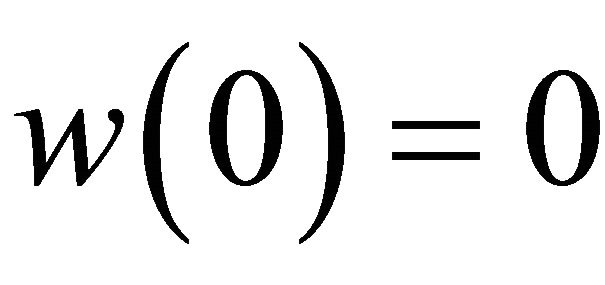 ,
, 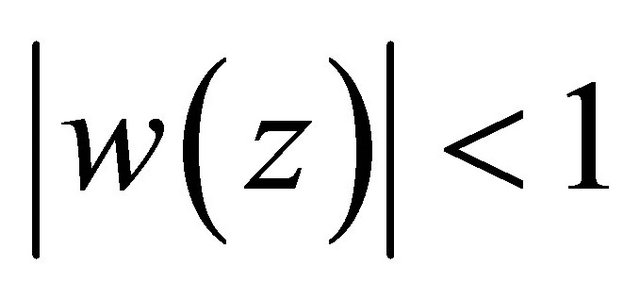 and
and . We also observe that
. We also observe that
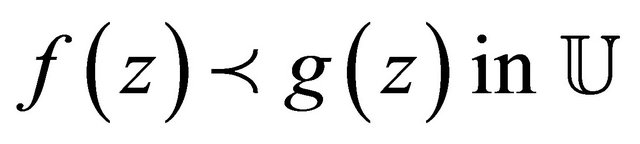
if and only if

whenever  is univalent in
is univalent in .
.
Let a, b and c be complex numbers with . Then the Gaussian/classical hypergeometric function
. Then the Gaussian/classical hypergeometric function  is defined by
is defined by
 (1.2)
(1.2)
where  is the Pochhammer symbol defined, in terms of the Gamma function, by
is the Pochhammer symbol defined, in terms of the Gamma function, by
 (1.3)
(1.3)
The hypergeometric function  is analytic in
is analytic in  and if a or b is a negative integer, then it reduces to a polynomial.
and if a or b is a negative integer, then it reduces to a polynomial.
For each A and B such that , let us define the function
, let us define the function
 (1.4)
(1.4)
It is well known that , for
, for , is the conformal map of the unit disk onto the disk symmetrical respect to the real axis having the center
, is the conformal map of the unit disk onto the disk symmetrical respect to the real axis having the center  and the radius
and the radius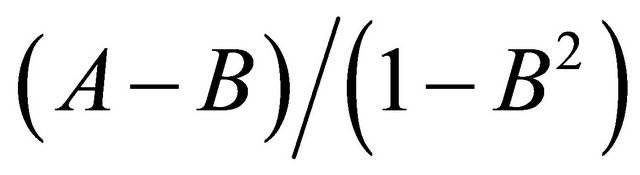 . The boundary circle cuts the real axis at the points
. The boundary circle cuts the real axis at the points  and
and .
.
Many essentially equivalent definitions of fractional calculus have been given in the literature (cf., e.g. [2,3]). We state here the following definition due to Saigo [4] (see also [1,5]).
Definition 1. For ,
,  , the fractional integral operator
, the fractional integral operator  is defined by
is defined by
 (1.5)
(1.5)
where  is the Gaussian hypergeometric function defined by (1.2) and
is the Gaussian hypergeometric function defined by (1.2) and  is taken to be an analytic function in a simply-connected region of the z-plane containing the origin with the order
is taken to be an analytic function in a simply-connected region of the z-plane containing the origin with the order
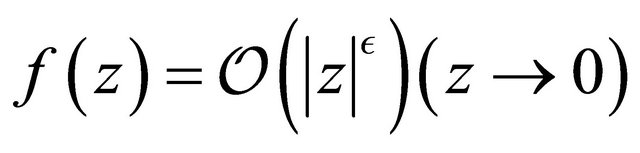
for , and the multiplicity of
, and the multiplicity of  is removed by requiring that
is removed by requiring that 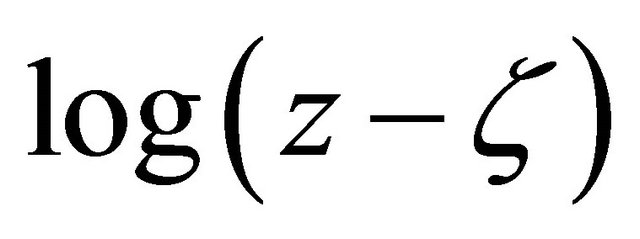 to be real when
to be real when .
.
The definition (1.5) is an interesting extension of both the Riemann-Liouville and Erdélyi-Kober fractional operators in terms of Gauss’s hypergeometric functions.
With the aid of the above definition, Owa, Saigo and Srivastava [1] defined a modification of the fractional integral operator  by
by
 (1.6)
(1.6)
for  and
and . Then it is observed that
. Then it is observed that  also maps
also maps 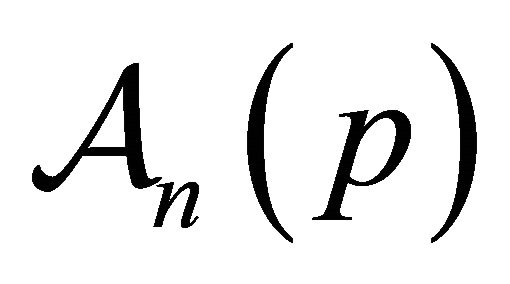 onto itself as follows:
onto itself as follows:
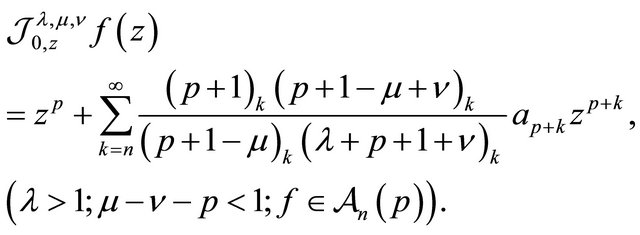 (1.7)
(1.7)
We note that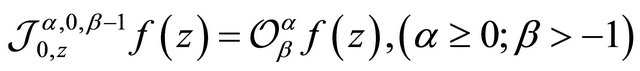 , where the operator
, where the operator 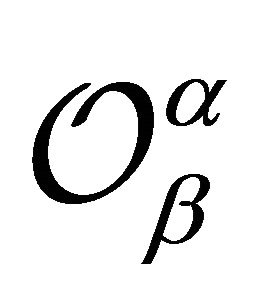 was introduced and studied by Jung, Kim and Srivastava [6] (see also [7]).
was introduced and studied by Jung, Kim and Srivastava [6] (see also [7]).
It is easily verified from (1.7) that
 (1.8)
(1.8)
The identity (1.8) plays an important and significant role in obtaining our results.
Recently, by using the general theory of differential subordination, several authors (see, e.g. [7-9]) considered some interesting properties of multivalent functions associated with various integral operators. In this manuscript, we shall derive some subordination properties of the fractional integral operator  by using the technique of differential subordination.
by using the technique of differential subordination.
2. Main Results
In order to establish our results, we shall need the following lemma due to Miller and Mocanu [10].
Lemma 1. Let  be analytic and convex univalent in
be analytic and convex univalent in  with
with , and let
, and let 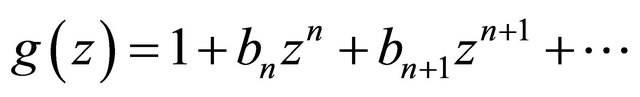 be analytic in
be analytic in . If
. If
 (2.1)
(2.1)
then for  and
and ,
,
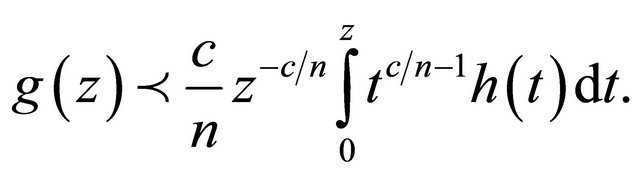 (2.2)
(2.2)
We begin by proving the following theorem.
Theorem 1. Let ,
,  ,
,  ,
,  ,
,  and
and , and let
, and let
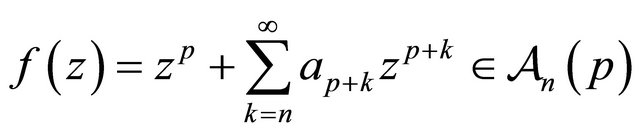 . Suppose that
. Suppose that
 (2.3)
(2.3)
where
 (2.4)
(2.4)
and  is given by (1.3).
is given by (1.3).
1) If , then
, then
 (2.5)
(2.5)
2) If  and
and , then
, then
 (2.6)
(2.6)
The result is sharp.
Proof. 1) If we set
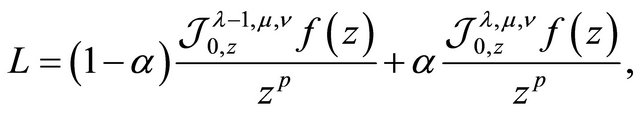
then, from (1.7) we see that
 (2.7)
(2.7)
For  and
and , it follows from (2.3) that
, it follows from (2.3) that
 (2.8)
(2.8)
which implies that

2) Let
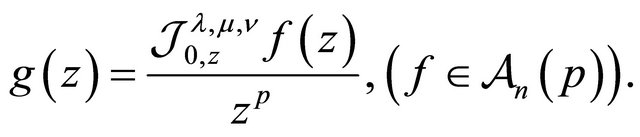 (2.9)
(2.9)
Then the function  is analytic in
is analytic in . Using (1.8) and (2.9), we have
. Using (1.8) and (2.9), we have
 (2.10)
(2.10)
From (2.5), (2.9) and (2.10) we obtain

Thus, by applying Lemma 1, we observe that

or
 (2.11)
(2.11)
where  is analytic in
is analytic in  with
with  and
and . In view of
. In view of  and
and  , we conclude from (2.11) that
, we conclude from (2.11) that
 (2.12)
(2.12)
Since 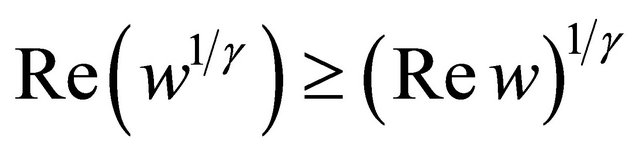 for
for  and
and , from (2.12) we see that the inequality (2.6) holds.
, from (2.12) we see that the inequality (2.6) holds.
To prove sharpness, we take  defined by
defined by
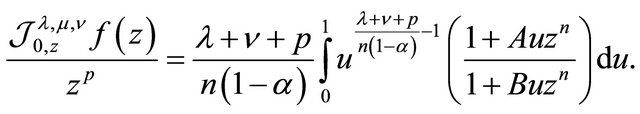
For this function we find that

and

Hence the proof of Theorem 1 is evidently completed.
Theorem 2. Let ,
, 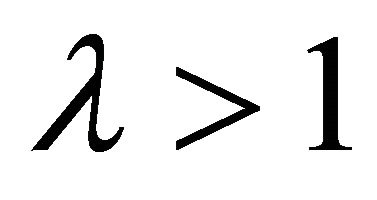 ,
,  ,
,  ,
,  and
and . Suppose that
. Suppose that
 ,
,  and
and  . If the sequence
. If the sequence 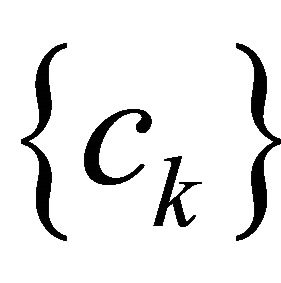 is nondecreasing with
is nondecreasing with
 (2.13)
(2.13)
where 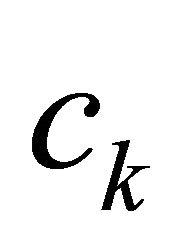 is given by
is given by  and satisfies the condition
and satisfies the condition , then
, then
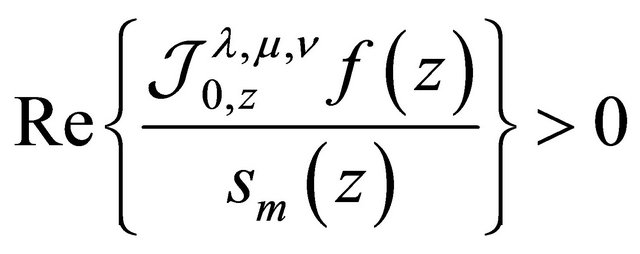 (2.14)
(2.14)
and
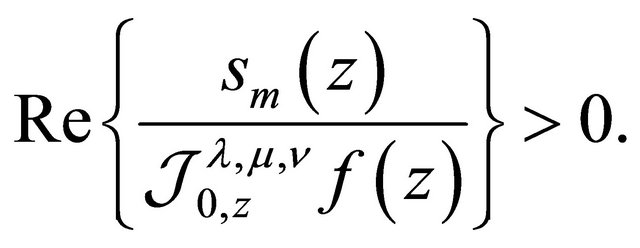 (2.15)
(2.15)
Each of the bounds in (2.14) and (2.15) is best possible for .
.
Proof. We prove the bound in (2.14). The bound in (2.15) is immediately obtained from (2.14) and will be omitted. Let

Then, from (1.7) we observe that

where, for convenience,

It is easily seen from (2.4) and (2.13) that  and
and
 (2.16)
(2.16)
Hence, by applying (2.3) and (2.16), we have
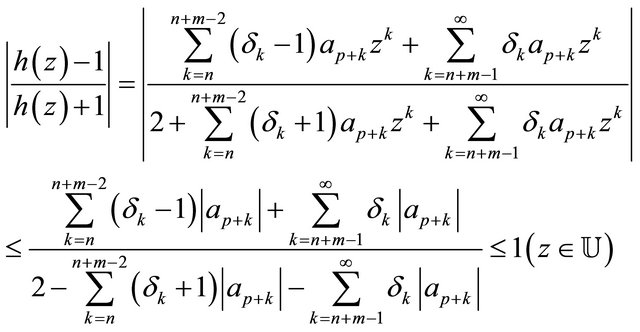
which readily yields the inequality (2.14).
If we take , then
, then

This show that the bound in (2.14) is best possible for each m, which proves Theorem 2.
Finally, we consider the generalized Bernardi-LiveraLivingston integral operator  defined by (cf. [11-13])
defined by (cf. [11-13])
 (2.17)
(2.17)
Theorem 3. Let ,
,  ,
,  ,
,  ,
,  ,
,  and
and and let
and let . Suppose that
. Suppose that
 (2.18)
(2.18)
where

and  is given by (1.3).
is given by (1.3).
1) If , then
, then
 (2.19)
(2.19)
2) If 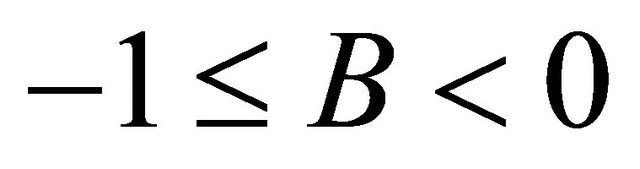 and
and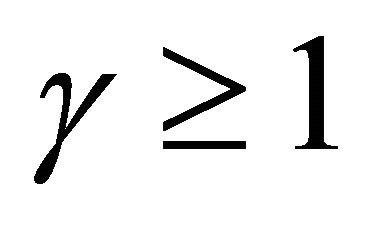 , then
, then
 (2.20)
(2.20)
The result is sharp.
Proof. 1) If we put

then, from (1.7) and (2.17) we have

Therefore, by using same techniques as in the proof of Theorem 1 1), we obtain the desired result.
2) From (2.17) we have
 (2.21)
(2.21)
Let
 (2.22)
(2.22)
Then, by virtue of (2.21), (2.22) and (2.19), we observe that

Hence, by applying the same argument as in the proof of Theorem 1 2), we obtain (2.20), which evidently proves Theorem 3.
3. Acknowledgements
This work was supported by Daegu National University of Education Research grant in 2011.