On Approximate Solutions of Second-Order Linear Partial Differential Equations ()
1. Introduction
Let the second-order partial differential equation be in the form [1,2]
We assume that it has a Chebyshev series solution in the form
(1.2)
where 
denotes a sum whose first term is halved. The unknown coefficients 
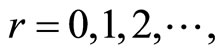
can be determined by using so called Chebyshev matrix method.
2. Calculation of Chebyshev Coefficients
Let we have a function
, 
and its nth derivatives with respect to x can be expanded in Chebyshev series
and
Respectively, where 
and 
are Chebyshev coefficients; clearly, 
and 
. Then the recurrence relation between the coefficients of 
and 
is obtained as
(2.1)
From Equation (2.1), we can deduce the relations
And adding these side by side, we get
or
(2.2)
Specially, we can express the coefficients 
and 
in terms of the 
by means of Equation (2.2), in the forms
(2.3)
and
or
(2.4)
Now, let us take 
and assume 
for
; then the system (2.2) can be transformed into the matrix form,
(2.5)
where M is given in [3].
For 
it follows from Equation (2.5) that
(2.6)
where clearly
.
Let us assume, in the range
, that the nth derivatives of 
with respect to y can be expanded in Chebyshev series
Respectively, where 
and 
are Chebyshev coefficients; clearly 
and 
. Then the recurrence relation between the coefficients of 
and 
is obtained as
(2.7)
From Equation (2.7), we can deduce the relations
and adding these side by side, we get
or
(2.8)
Specially, we can express the coefficients 
and 
in terms of the
, by means of Equation (2.8), in the forms
(2.9)
and
or
(2.10)
Now, let us take 
and assume 
for
; then the system (2.8) can be transformed into the matrix form,
(2.11)
where
For 
it follows from Equation (2.11) that
(2.12)
where clearly
. Furthermore, 
can be expressed as follows:
(2.13)
3. Fundamental Relations
Now consider Equation (1.1), where A, B, C, D, E, F and G are functions of x and y, or constant, defined in the range
. Our purpose is to investigate the truncated Chebyshev series solution of Equation (1.1), under the given conditions, in the series form
or in the matrix form
(3.1)
where
, 
are the Chebyshev coefficients to be determined 
are the bivariate Chebyshev polynomials defined in [4], and matrices
, 
and A are defined by
To obtain the solution of Equation (1.1) in the form of Equation (3.1), first we must reduce Equation (1.1) to a differential Equation whose coefficients are polynomials [5]. For this purpose, we assume that the functions
, 
, 
, 
, 
, 
, and 
can be expressed in the form
(3.2)
Which are Taylor polynomials at
. By using the expressions (3.2) in Equation (1.1), we get
(3.3)
The Chebyshev expansions of terms
in Equation (3.3) are obtained by means of the formulae
(3.4)
4. Matrix Forms of Terms in the Equation
The matrix representation of Equation (3.4) can be given by
(4.1)
(4.2)
(4.3)
(4.4)
(4.5)
(4.6)
(4.7)
where 
and
, 
.
And for
;
, 
(
and
) is a matrix of size
. The elements of Mp are given in [6].
Substituting the expressions (4.1)-(4.7) into Equation (3.3), and simplifying the result, we have the matrix equation
(4.8)
Which corresponds to a system 
algebraic equations for the unknown Chebyshev coefficients
. Briefly, we can assume that Equation (4.8) is given in the form
(4.9)
where 
Matrix Equation (4.9) can be reduce to new matrix equation by making use of
Then the new matrix Equation (4.7) becomes
(4.10)
where
and
5. Matrix Forms of Conditions
Let the conditions of Equation (1.1) be given by
(5.1)
(5.2)
(5.3)
where f is a function of x, g is a function of y and 
is constant.
Then, there are the following matrix forms at x = −1, 0, 1 and similar way for y = −1, 0, 1;
Derivative of Tx at x = −1, 0, 1 and similar way for y = −1, 0, 1;
We assume that the functions 
and 
can be expanded as
and
or in the matrix form
and
where
In addition, at x = −1, 0, 1 and y = −1, 0, 1, we obtain the matrix forms
Substituting theses matrices forms into conditions (5.1)-(5.3), and then simplifying, we get the fundamental matrix equations of conditions as follows:
(5.4)
where
6. Former Method for the Solution
We can assume that Equation (6.1) is in the form
(6.1)
where
.
Then the augmented matrix of Equation (6.1) becomes 
or
(6.2)
If we take the new matrix forms of the conditions as
, 
and
, respectively, the augmented matrices of them become
, 
and 
or more clearly
(6.3)
(6.4)
and
(6.5)
Consequently, by replacing Equations (6.3)-(6.5) by the last 2N + 1 rows of Equation (6.2), we have the new augment matrix
From the solution of this system we can find matrix C or matrix A.
7. Applications
The Chebyshev matrix method applied in this study is useful in finding approximate solutions of second-order linear partial differential equations in both homogeneous and non-homogeneous cases, in terms of Chebyshev polynomials. We illustrate it by the following examples.
Example 1. We now consider the problem [7]:
(1)
And seek the solution in the form
(2)
Then we obtain the matrix equation
(3)
where
And the condition matrices are
(4)
(5)
By replacing the new matrix form of Equations (4) and (5) in the new matrix form of Equation (3), we have the matrix equation under given conditions as follows:
Hence, we obtain the augmented matrix
The solution of this system is
and thereby the solution of the problem (1) becomes
or
This is exact solution [7].
Example 2
Let us now study the equation
with conditions which are
The first four terms of the series expansions:
Chebyshev matrix forms of the conditions,
Matrix form of the equation is
From the solution of this matrix equation under the given conditions, we get the Chebyshev coefficients matrix as
The solution of problem is obtained as
Which is the first four terms of
.
8. Conclusions
Analytic solutions of the second order linear partial differential equations with variable coefficients are usually difficult. In many cases, it is required to approximate solutions. For this purpose, the Chebyshev matrix method can be proposed.
In this study, the usefulness of the Chebyshev matrix method presented for the approximate solution of the second order linear partial differential equations is discussed. Also, the method can be applied to both the nonhomogeneous and homogeneous cases.
A considerable advantage of the method is that the solution is expressed as a truncated Chebyshev series and thereby a Taylor polynomial. Furthermore, after calculation of the series coefficients, the solution 
of the equations can be easily evaluated for arbitrary values of 
at low computation effort.
An interesting feature of the Chebyshev matrix method is that the method can be used in finding exact solutions in much cases. The method can be also extending to the solution of the higher order linear partial differential equations.