Calculation of Particle Decay Times in the Standard Model

Jan Helm

Department of Electrical Engineering, Technical University, Berlin, Germany.

DOI: 10.4236/jmp.2024.153014                

Abstract

We present here a two-step method of classification and calculation for decay rates in the Standard Model. The first step is a phenomenological classification method, which is an extended and improved schematic experimental formula for decay width originally introduced by Chang. This schematic formula separates decays into seven classes. Furthermore, from it is derived a process-specific interaction energy m_X. The second step is a numerical calculation method, which calculates this interaction energy m_X numerically by minimization of action from the Lagrangian of the process, from which follows the decay width via the phenomenological formula. The Lagrangian is based on an extension of the Standard Model, the extended SU(4)-preon-model. A comparison of numerically calculated and observed decay widths for a large selection of decays shows a good agreement.

Keywords

Particle Decay, Decay Width, Interaction Energy, Minimization of Action, Ex-tension of Standard Model

1. Introduction

The particle decays in the Standard Model are characterized by their decay width Γ (or equivalently decay rate ${\Gamma }_d=\Gamma /\hslash$ ), and are described by the famous Fermi’s golden rule, i.e. an integral with parameters.

A closed expression for Γ can be found in only a few cases, otherwise there are empirical formulas, or simply data tables.

We present here a two-step calculation method for calculation of general decay rates in the Standard Model.

The first step is a phenomenological classification method, which is an improved and generalized schematic formula for decay width originally introduced by Chang [1] . It is a general parameterized approximation formula with some special cases, which is in good agreement with measurements.

It introduces seven classes of particle decays, where the interaction constant is roughly class-specific. In other words, it allows to extrapolate and make assessments for decays, for which there is no analytic formula. Furthermore, it supports the notion of decay-mediating virtual particle with interaction energy m_X.

The second step is a numerical Lagrangian calculation method for interaction energy m_X, which calculates the interaction energy of the process numerically by minimization of action from the Lagrangian of the process. From the interaction energy follows the decay width using the phenomenological formula. A comparison of numerically calculated and observed decay widths for a large selection of decays shows a good agreement.

The starting point for decay rate ${\Gamma }_d=\Gamma /\hslash$ , or equivalently, its decay width Γ, of a n-body process

$\Gamma \left(P_0\left(k,m\right)\to P\left(p_1,m_1\right)P\left(p_2,m_2\right)P\left(p_3,m_3\right)\cdots P\left(p_n,m_n\right)\right)$

is the Fermi’s golden rule

$\begin{array}{l}\text{d}\Gamma =m\frac{{\left|M\left(k,p_1,p_2,p_3,\cdots ,p_n\right)\right|}^2}{2}\frac{{\text{d}}^3{p}_1}{{\left(2\pi \right)}^{3}2m^2{E}_1}\frac{{\text{d}}^3{p}_2}{{\left(2\pi \right)}^{3}2m^2{E}_2}\frac{{\text{d}}^3{p}_3}{{\left(2\pi \right)}^{3}2m^2{E}_3}\cdots \\ \frac{{\text{d}}^3{p}_n}{{\left(2\pi \right)}^{3}2m^2{E}_n}{\left(2\pi \right)}^4{m}^4{\delta }^4\left(k-\left(p_1+p_2+p_3+\cdots +p_n\right)\right)\end{array}$

We demonstrate in chap.2 at selected examples, how to derive Γ from Fermi’s golden rule in a closed form, which in general has to be done numerically.

For 2-body decays and 3-body decays we can (approximately) split-off the kinematic factor $I_{\Gamma }$ of Γ, taking the transition matrix out of the integral.

The phenomenological classification method is described in chap.3 and chap. 5, and the calculated ${\Gamma }_{calc}$ are compared with measured ${\Gamma }_{obs}$ in chap.6.

The phenomenological formula for the decay width is [1] .

$\Gamma ={\tilde{G}}^2{m}_i^k{\left|P_l{}^m\left(x\right)\right|}^2=\frac{G^2}{C_1}{m}_i^k{\left|P_l{}^m\left(x\right)\right|}^2$ , where $P_l{}^m\left(x\right)$ Legendre polynomial m = l or m = l + 1, l = isospin I, $x=\frac{m_f}{m_i}$ mass ratio, $\tilde{G}=\frac{G}{\sqrt{C_1}}$ with G = interaction

constant, $m_i$ is the initial mass, k is the mass-power-coefficient.

We introduce and derive the interaction energy m_X in the form

$\Gamma ={\left|M\right|}^2{I}_{\Gamma }{m}_i={\left(\frac{m_i^2}{8m_X^2}\right)}^2{I}_{\Gamma }{m}_i$ .

The numerical calculation method is based on an extended version of the Standard Model (SM) introduced by Helm [2] , called the extended SU(4)-preon-model (SU4PM). In SU4PM, the Pauli SU(2)-weak interaction is extended to SU(4)-hypercolor (hc) interaction with four charges, 15 hc-boson fields and two subparticles called preons, and SU(2)-weak interaction becomes a Yukawa-approximation via massive (W, Z)-bosons.

The SU4PM model allows to calculate the masses of the SM remarkably well, reducing 29 parameters of the SM to 7.

In chap. 7, we calculate the interaction energy m_X numerically by minimization of action of the SU4PM Lagrangian of the particles in the decay process, and we obtain a good agreement between the calculated values $m_{Xcal}$ and observed values $m_{Xexp}$ .

A remark about units: in particle physics it is customary to use the convention $\hslash =c=1$ , and we adopt it here as well, except in places, where quantities have to be distinguished, e.g. decay width Γ is an energy and is measured in MeV: $\left[\Gamma \right]=\text{MeV}$ , whereas decay rate ${\Gamma }_d=\Gamma /\hslash$ is measured in s⁻¹: $\left[{\Gamma }_d\right]={\text{s}}^{-1}$ .

Other quantities are transformed from each other by $\hslash$ and c, e.g. mass $m=E/c^2$ , time $t=\hslash /E$ , length $x=\hslash c/E$ , angular momentum $p=E/c$ .

The contents of the paper is as follows.

In chap. 2, first some important decays are discussed, and in 1.8 and 1.9 the general decay width formula for 3-body and 2-body decays.

In chap. 3 the phenomenological formula for the decays is presented, and is discussed for some important decays.

Chap. 4 shows the data of the most important particles.

In chap. 5, the phenomenological formula values and the observed values for the decay width, together with the decay interaction energy m_X are discussed.

In chap. 6 the phenomenological decay width, the observed decay width, and the interaction energy are shown in a table and in a plot, and generally characterized.

In chap. 7, we present a calculation method and a reaction model using electromagnetic, color SU(3), and extended weak SU(4) interaction based on SU4PM model.

Here, the theoretical background and the calculation software is discussed, and the calculated results for $m_{Xcal}$ are compared to the observed values $m_{Xexp}$ from chap. 5, and shown in a table and in plots.

2. Selected Particle Decays with Theoretical Background

In this chapter we discuss some well-understood particle decays, with decay width described by an analytical formula [3] [4] [5] [6] [7] .

2.1. Neutron

The free neutron decays into a proton, electron, and antineutrino [8] is shown in Figure 1.

$n\to p+e^{-}+{\bar{\nu }}_e$

The rest energy $\left(m_n-m_p-m_e\right)c^2=782\text{keV}$ is carried away by e and ν

The transition matrix of the decay is [8] [10]

$M=\left(G_V\bar{p}{\gamma }^{\mu }n-G_A\bar{p}{\gamma }^{\mu }{\gamma }_{5}n\right)\left(\bar{e}{\gamma }_{\mu }\left(1-{\gamma }_5\right)\nu \right)\delta \left(E_n-E_p-E_e-E_{\nu }\right)$

from the interaction Hamiltonian [10]

Figure 1. Neutron decay [9] .

$H_{\mathrm{int}}=G_F{V}_{ud}\left(\bar{p}{\gamma }^{\mu }\left(1-\frac{G_A}{G_V}{\gamma }_5\right)n\right)\left(\bar{e}{\gamma }_{\mu }\left(1-{\gamma }_5\right)\nu \right)$

with $G_A/G_V=1.255\pm 0.005$

$E\left(G_V\right)=\frac{1}{\sqrt{G_V}}=296.7\text{GeV}$

$G_F=1.1663787\left(6\right)\times {10}^{-5}{\text{GeV}}^{-2}$ is the Fermi weak coupling constant, $V_{ud}=0.97417\left(21\right)$ (V is the CKM-matrix),

and the weak V-constant is

$G_V=G_F{V}_{ud}=1.135\times {10}^{-5}{\text{GeV}}^{-2}$ , $G_A=G_F{V}_{ud}\lambda$ and λ is the hadronic strong interaction correction.

We compute the neutron decay probability per unit time using Fermi’s golden rule [11] :

${\Gamma }_{i\to f}=\frac{2\pi }{\hslash }{\left|\langle f\left|H\right|i\rangle \right|}^2\rho \left(E_f\right)$ , where $\rho \left(E_f\right)$ = final state energy density

or in differential form [11]

$\text{d}\Gamma =\frac{{\left|M\left(k_1,k_2,k_3,k_4\right)\right|}^2}{2m_1}\frac{{\text{d}}^3{k}_2}{{\left(2\pi \right)}^{3}2E_2}\frac{{\text{d}}^3{k}_3}{{\left(2\pi \right)}^{3}2E_3}\frac{{\text{d}}^3{k}_4}{{\left(2\pi \right)}^{3}2E_4}{\left(2\pi \right)}^4{\delta }^4\left(k_1-k_2-k_3-k_4\right)$ (1)

where $k_1=p_n$ , $k_2=p_p$ , $k_3=p_e$ , $k_4=p_{\nu }$ , $m_1=m_n$ with the (dimensionless) transition matrix $M\left(k_1,k_2,k_3,k_4\right)=\langle f\left|H_{\mathrm{int}}\right|i\rangle \delta \left(E_f-E_i\right)$ of the interaction Hamiltonian $H_{\mathrm{int}}$ .

Here E_e, p_e, E_n, and p_n are the electron and antineutrino total energy and momentum Δ is the neutron-proton mass difference $\Delta =1.29333205\left(51\right)\text{MeV}$ .

Integration over the antineutrino and electron momenta gives the beta electron energy spectrum

$\frac{\text{d}\Gamma }{\text{d}E}=\frac{G_V^2+3G_A^2}{2{\pi }^3}{E}_e{p}_e{\left(\Delta -E_e\right)}^2$

Additional integration over electron energy yields

$\Gamma =\left(G_V^2+3G_A^2\right)\frac{m_e^5}{2{\pi }^3}{f}_R$

Here f_R is the phase-space term, i.e. the value of the integral over the Fermi energy spectrum, including Coulomb, recoil order, and radiative corrections.

The decay width of the decay becomes [8]

$\Gamma \left(n\to pe{\nu }_e\right)=\left(G_V^2+3G_A^2\right)\frac{m_e^5}{2{\pi }^3}{f}_R=G_F^2{V}_{ud}^2\left(1+3{\lambda }^2\right)\frac{m_e^5}{2{\pi }^3}{f}_R$ (2)

where $G_V=G_F{V}_{ud}$ , $G_A=G_F{V}_{ud}\lambda$ , $\lambda =1.255$ , $V_{ud}=0.974$ , $G_F=1.166\times {10}^{-5}{\text{GeV}}^{-2}$

with the phase-space term [9] $f_R\left(\xi \right)=\frac{1}{60}\left(2{\xi }^4-9{\xi }^2-8\right){\left({\xi }^2-1\right)}^{1/2}+\frac{1}{4}\xi \ln \left(\xi +{\left({\xi }^2-1\right)}^{1/2}\right)$ , $\xi =\frac{m_n-m_p}{m_e}$ ,

$f_R=1.6332$

here the transition probability per unit time is $W=\Gamma \left(n\to pe{\nu }_e\right)/\hslash$ .

The neutron lifetime τ_n becomes

${\tau }_n=\hslash /\Gamma \left(n\to pe{\nu }_e\right)=\frac{2{\pi }^3}{\left(G_V^2+3G_A^2\right)m_e^5{f}_R}=881.5\text{s}$

2.2. Muon

The muon decays into an electron, an electron-antineutrino and a muon-neutrino is shown in Figure 2.

$\mu \to e^{-}+{\bar{\nu }}_e+{\nu }_{\mu }$

For the muon decay we derive the formula for the decay width Γ [6] [12] .

The interaction Hamiltonian is the current-current interaction

$H_{\mathrm{int}}=\frac{g^2}{2M_W^2}{\bar{u}}_2\left(k_2,s_2\right)\left({\gamma }^{\mu }\frac{1-{\gamma }^5}{2}\right)u_1\left(k_1,s_1\right){\bar{u}}_4\left(k_4,s_4\right)\left({\gamma }_{\mu }\frac{1-{\gamma }^5}{2}\right)u_3\left(k_3,s_3\right)$

From the transition matrix element

Figure 2. Muon decay [9] .

$M=\frac{g^2}{2M_W{}^2}{\bar{u}}_2\left(k_2,s_2\right)\left({\gamma }^{\mu }\frac{1-{\gamma }^5}{2}\right)u_1\left(k_1,s_1\right){\bar{u}}_4\left(k_4,s_4\right)\left({\gamma }_{\mu }\frac{1-{\gamma }^5}{2}\right)u_3\left(k_3,s_3\right)\delta \left(E_1-E_2-E_3-E_4\right)$

with $\frac{G}{\sqrt{2}}=\frac{g^2}{8M_W^2}$ and G = G_F, g is the weak dimensionless interaction constant,

we obtain after some γ-algebra averaging over the spins and trace-manipulation.

${\left|M\left(k_1,k_2,k_3,k_4\right)\right|}^2=64G^2\left(k_1\cdot k_3\right)\left(k_2\cdot k_4\right)$ and for the decay rate we have Fermi’s golden rule

$\text{d}\Gamma =\frac{{\left|M\left(k_1,k_2,k_3,k_4\right)\right|}^2}{2m}\frac{{\text{d}}^3{k}_2}{{\left(2\pi \right)}^{3}2E_2}\frac{{\text{d}}^3{k}_3}{{\left(2\pi \right)}^{3}2E_3}\frac{{\text{d}}^3{k}_4}{{\left(2\pi \right)}^{3}2E_4}{\left(2\pi \right)}^4{\delta }^4\left(k_1-k_2-k_3-k_4\right)$

$\text{d}\Gamma =\frac{64G^2}{2m}\left(\left(k_1\cdot k_3\right)\left(k_2\cdot k_4\right)\right)\frac{{\text{d}}^3{k}_2}{{\left(2\pi \right)}^{3}2E_{k_2}}\frac{{\text{d}}^3{k}_3}{{\left(2\pi \right)}^{3}2E_{k_3}}\frac{{\text{d}}^3{k}_4}{{\left(2\pi \right)}^{3}2E_{k_4}}{\left(2\pi \right)}^4{\delta }^4\left(k_1-k_2-k_3-k_4\right)$

In the muon rest frame $k_1=\left(m,0,0,0\right)$ and $\left(k_1\cdot k_3\right)=m{E}_3$ and with $k_1=k_2+k_3+k_4$

$\text{d}\Gamma =\frac{G^2}{8m{\pi }^5}\left(\left(k_2\cdot k_4\right)m{E}_3\right)\frac{{\text{d}}^3{k}_2}{\left|{\stackrel{\to }{k}}_2\right|}\frac{{\text{d}}^3{k}_3}{\left|{\stackrel{\to }{k}}_3\right|}\frac{{\text{d}}^3{k}_4}{\left|{\stackrel{\to }{k}}_4\right|}\delta \left(m-\left|{\stackrel{\to }{k}}_2\right|-\left|{\stackrel{\to }{k}}_3\right|-\left|{\stackrel{\to }{k}}_4\right|\right){\delta }^3\left({\stackrel{\to }{k}}_2+{\stackrel{\to }{k}}_3+{\stackrel{\to }{k}}_4\right)$

in spherical coordinates

$\text{d}\Gamma =\frac{m{G}^2{\left|{\stackrel{\to }{k}}_3\right|}^2}{8{\pi }^4}\left(m-2\left|{\stackrel{\to }{k}}_3\right|\right)\frac{\sin \theta \text{d}\theta \text{d}\left|{\stackrel{\to }{k}}_3\right|{\text{d}}^3{k}_4}{\left({\left|{\stackrel{\to }{k}}_3\right|}^2+{\left|{\stackrel{\to }{k}}_4\right|}^2+2\left|{\stackrel{\to }{k}}_3\right|\left|{\stackrel{\to }{k}}_4\right|\cos \theta \right)\left|{\stackrel{\to }{k}}_4\right|}\delta \left(m-\left|{\stackrel{\to }{k}}_3+{\stackrel{\to }{k}}_4\right|-\left|{\stackrel{\to }{k}}_3\right|-\left|{\stackrel{\to }{k}}_4\right|\right)$

with variable $u^2={\left|{\stackrel{\to }{k}}_3\right|}^2+{\left|{\stackrel{\to }{k}}_4\right|}^2+2\left|{\stackrel{\to }{k}}_3\right|\left|{\stackrel{\to }{k}}_4\right|\cos \theta$

$\text{d}\Gamma =\frac{m{G}^2\left|{\stackrel{\to }{k}}_3\right|}{8{\pi }^4}\left(m-2\left|{\stackrel{\to }{k}}_3\right|\right)\frac{\text{d}\left|{\stackrel{\to }{k}}_3\right|{\text{d}}^3{k}_4}{{\left|{\stackrel{\to }{k}}_4\right|}^2}{\displaystyle \int \text{d}u\delta \left(m-u^2-\left|{\stackrel{\to }{k}}_3\right|-\left|{\stackrel{\to }{k}}_4\right|\right)}$ ,

and with E = k₄

we obtain

$\frac{\text{d}\Gamma }{\text{d}E}=\frac{m{G}^2}{2{\pi }^3}{E}^2\left(\frac{m}{2}-\frac{2E}{3}\right)$

$\Gamma =\frac{m^2{G}^2}{4{\pi }^3}{\displaystyle \underset{0}{\overset{m/2}{\int }}{E}^2\left(1-\frac{4E}{3m}\right)\text{d}E}$ , $\Gamma =\frac{m^5{G}^2}{192{\pi }^3}$ (3)

and the decay time $\tau =\hslash {\Gamma }^{-1}$ ,

where $m=0.1056584\text{GeV}$

$\tau =\hslash \frac{192{\pi }^3}{{\left(0.1056584\text{GeV}\right)}^5{\left(1.17\times {10}^{-5}{\text{GeV}}^{-2}\right)}^2}=\hslash 3.30\times {10}^{18}\text{GeV}$ ,

or in seconds, multiplied by $\hslash =6.58\times {10}^{-25}\text{s}\cdot \text{GeV}$ ,

we obtain the lifetime $\tau =2.17\mu \text{s}$ .

2.3. Tauon

The decay modes of the tauon are

$\tau \to \mu +{\bar{\nu }}_{\mu }+{\nu }_{\tau }$

$\tau \to e+{\bar{\nu }}_e+{\nu }_{\tau }$

$\tau \to d+\bar{u}+{\nu }_{\tau }$

$\tau \to s+\bar{u}+{\nu }_{\tau }$

The leptonic modes give a factor $f_l=2$ , the hadronic modes a factor $f_h=3{\left|V_{ud}\right|}^2+3{\left|V_{us}\right|}^2=2.99$ ,

and $m_{\tau }=16.82m_{\mu }$

$t_{life}\left(\tau \right)=\frac{t_{life}\left(\mu \right)}{\left(f_l+f_h\right){\left(m_{\tau }/m_{\mu }\right)}^2}=3.23\times {10}^{-13}\text{s}$

2.4. Pions

The particle data for the pions are shown in Table 1.

Charged pion decays

The diagram of charged pion decays is shown in Figure 3.

The π^± mesons have a mass of 139.6 MeV/c² and a mean lifetime of 2.6033 × 10⁻⁸ s. They decay due to the weak interaction. The primary decay mode of a pion, with a branching fraction of 0.999877, is a leptonic decay into a muon and a muon neutrino:

${\pi }^{+}\to {\mu }^{+}+{\nu }_{\mu }$

${\pi }^{-}\to {\mu }^{-}+{\bar{\nu }}_{\mu }$

The pion-muon decay width is [14]

$\Gamma =f_{\pi }^2\frac{G^2}{8\pi }{m}_{\pi }^3{m}_{\mu }^2{\left(1-\frac{m_{\mu }^2}{m_{\pi }^2}\right)}^2$

Table 1. Parameters of the pions.

Figure 3. Feynman diagram of the dominant leptonic pion decay [13] .

where $f_{\pi }$ is the (dimensionless) pion decay factor, $f_{\pi }=\frac{130.41\text{MeV}}{m_{\pi }}=0.934$ .

The second most common decay mode of a pion, with a branching fraction of 0.000123, is also a leptonic decay into an electron and the corresponding electron antineutrino. This “electronic mode” was discovered at CERN in 1958

${\pi }^{+}\to e^{+}+{\nu }_e$

${\pi }^{-}\to e^{-}+{\bar{\nu }}_e$

The suppression of the electronic decay mode with respect to the muonic one is given approximately (up to a few percent effect of the radiative corrections) by the ratio of the half-widths of the pion-electron and the pion-muon decay reactions:

$R_{\pi }={\left(m_e/m_{\mu }\right)}^2{\left(\frac{m_{\pi }^2-m_e^2}{m_{\pi }^2-m_{\mu }^2}\right)}^2=1.283\times {10}^{-4}$

and is a spin effect known as helicity suppression.

Also observed, for charged pions only, is the very rare “pion beta decay” (with branching fraction of about 10⁻⁸) into a neutral pion, an electron and an electron antineutrino (or for positive pions, a neutral pion, a positron, and electron neutrino).

${\pi }^{+}\to {\pi }^0+e^{+}+{\nu }_e$

${\pi }^{-}\to {\pi }^0+e^{-}+{\bar{\nu }}_e$

The rate at which pions decay is a prominent quantity in many sub-fields of particle physics, such as chiral perturbation theory. This rate is parametrized by the pion decay constant (ƒ_π), related to the wave function overlap of the quark and antiquark, which is about 130 MeV.

Neutral pion decays

The π⁰ meson has a mass of 135.0 MeV/c² and a mean lifetime of 8.4 × 10⁻¹⁷ s. It decays via the electromagnetic force, which explains why its mean lifetime is much smaller than that of the charged pion (which can only decay via the weak force).

The neutral pion decay is shown in Figure 4.

The dominant π⁰ decay mode (anomaly-induced neutral pion decay), with a branching ratio of BR = 0.98823, is into two photons:

${\pi }^0\to \gamma +\gamma$

Figure 4. Anomaly-induced neutral pion decay [13] .

The second largest π⁰ decay mode (BR = 0.01174) is the Dalitz decay (named after Richard Dalitz), which is a two-photon decay with an internal photon conversion resulting a photon and an electron-positron pair in the final state:

${\pi }^0\to \gamma +e^{-}+e^{+}$

The third largest established decay mode (BR = 3.34 × 10⁻⁵) is the double Dalitz decay, with both photons undergoing internal conversion which leads to further suppression of the rate:

${\pi }^0\to e^{-}+e^{+}+e^{-}+e^{+}$

The fourth largest established decay mode is the loop-induced and therefore suppressed (and additionally helicity-suppressed) leptonic decay mode (BR = 6.46 × 10⁻⁸):

${\pi }^0\to e^{-}+e^{+}$

2.5. Pion-Nucleon Interaction and Decays

The Lagrangian is [6] [15]

$L=ig\bar{\psi }\left(x\right){\gamma }_5\stackrel{\to }{\sigma }\cdot \varphi \left(x\right)\psi (\; x\; )$

with pion $\varphi \left(x\right)=\left({\varphi }_1,{\varphi }_2,{\varphi }_3\right)$ , nucleon $\psi \left(x\right)=\left({\psi }_p,{\psi }_n\right)$ , and Pauli-matrix-vector $\stackrel{\to }{\sigma }$ , explicitly

$L=ig\left({\bar{\psi }}_p,{\bar{\psi }}_n\right){\gamma }_5\left(\begin{array}{cc}{\varphi }_3& {\varphi }_1-i{\varphi }_2\\ {\varphi }_1+i{\varphi }_2& {\varphi }_3\end{array}\right)\left({\psi }_p,{\psi }_n\right)\left({\varphi }_1,{\varphi }_2,{\varphi }_3\right)$

with Feynman diagrams shown in Figure 5.

and with the corresponding hadronic transformations

$p{\to }^{{\pi }^0}p$ , $n{\to }^{{\pi }^0}n$ , $n{\to }^{{\pi }^{-}}p$ , $p{\to }^{{\pi }^{+}}n$

Figure 5. Nucleon interaction via pions.

2.6. Kaons

Kaons exist in charged form ch-kaon = $\left(K^{+},K^{-}\right)$ and neutral form n-kaon = $\left(K^0,{\bar{K}}^0\right)$ , where n-kaon appears in nature as a symmetric and antisymmetric mixture of d and s: the long-lived kaon-L and the short-lived kaon-S.

The particle data for the kaons are shown in Table 2, their decay reactions in Table 3, and their quark decay processes in Figure 6.

Table 2. Parameters of the kaons.

Table 3. Main decay modes for K⁺ [16] .

Figure 6. Quark diagrams for K⁺ and K⁰ decays involving strangeness changing neutral currents [10] .

K0 decay and CP-violation

The full kaon-L and kaon-S contain a CP-violating term:

$K_L=\frac{1}{\sqrt{1+{\epsilon }^2}}\left(\frac{K^0+{\bar{K}}^0}{\sqrt{2}}+\epsilon \frac{K^0-{\bar{K}}^0}{\sqrt{2}}\right)$

$K_S=\frac{1}{\sqrt{1+{\epsilon }^2}}\left(\frac{K^0-{\bar{K}}^0}{\sqrt{2}}+\epsilon \frac{K^0+{\bar{K}}^0}{\sqrt{2}}\right)$

$\epsilon =2.25\times {10}^{-3}$ CP violation factor.

2.7. The Kaon-Pion Decay Detailed Theory

In [17] a semi-empirical formula for the transition matrix element $A_{++}$ in $\Gamma \left(K^{+}\left(k\right)\to {\pi }^{+}\left(p_1\right){\pi }^{+}\left(p_2\right){\pi }^{-}\left(p_3\right)\right)$ is derived.

First, the kinematic momentum variables s₀, s₁, s₂, s₃ are introduced

$s_1={\left(k-p_1\right)}^2$ , $s_2={\left(k-p_2\right)}^2$ , $s_3={\left(k-p_3\right)}^2$ , $s_0=\left(m^2+m_1^2+m_2^2+m_3^2\right)/3$

then, the Dalitz plot variables $x=\frac{s_2-s_1}{\left(m_1^2+m_2^2\right)/2}$ , $y=\frac{s_3-s_0}{m_3^2}$ are defined.

We obtain for $A_{++}$ (x,y) the expression

$\begin{array}{c}{A}_{++-}\left(x,y\right)=\left(-2{\alpha }_1+{\alpha }_3\right)+\left(-{\beta }_1+\frac{1}{2}{\beta }_3-\sqrt{3}{\gamma }_3\right)y\\ -\left(2{\zeta }_1+2{\zeta }_3\right)\left(y^2+\frac{1}{3}{x}^2\right)+\left({\xi }_1+{\xi }_3-{\xi }_3\text{'}\right)\left(y^2-\frac{1}{3}{x}^2\right)\end{array}$

with the constants:

${\alpha }_1=\left(91.71\pm 0.32\right)\times {10}^{-8}$ , ${\alpha }_2=\left(-7.36\pm 0.47\right)\times {10}^{-8}$ , ${\beta }_1=\left(-25.68\pm 0.27\right)\times {10}^{-8}$ , ${\beta }_2=\left(-2.43\pm 0.41\right)\times {10}^{-8}$ , ${\gamma }_3=\left(2.26\pm 0.23\right)\times {10}^{-8}$

${\zeta }_1=\left(-0.47\pm 0.15\right)\times {10}^{-8}$ , ${\zeta }_3=\left(-0.21\pm 0.08\right)\times {10}^{-8}$ , ${\xi }_1=\left(-1.51\pm 0.30\right)\times {10}^{-8}$ , ${\xi }_3=\left(-0.12\pm 0.17\right)\times {10}^{-8}$ , ${\xi }_3\text{'}=\left(-0.21\pm 0.51\right)\times {10}^{-8}$

and $m_2=m_3=m_1$ , $s_3={\left(p_1+p_2\right)}^2={\left(E_1+E_2\right)}^2-{\left({\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)}^2$ .

We obtain the following expression for the differential transition width from Fermi’s golden rule:

$\text{d}\Gamma =\frac{{\left|M\left(k,p_1,p_2,p_3\right)\right|}^2}{2m}\frac{{\text{d}}^3{p}_1}{{\left(2\pi \right)}^{3}2E_1}\frac{{\text{d}}^3{p}_2}{{\left(2\pi \right)}^{3}2E_2}\frac{{\text{d}}^3{p}_3}{{\left(2\pi \right)}^{3}2E_3}{\left(2\pi \right)}^4{\delta }^4\left(k-p_1-p_2-p_3\right)$

or, with Dalitz variables

$\text{d}\Gamma =\frac{{\left|M\left(k,p_1,p_2,p_3\right)\right|}^2}{2m}\frac{{\text{d}}^3{p}_1}{{\left(2\pi \right)}^{3}2\sqrt{m_1^2+p_1^2}}\frac{{\text{d}}^3{p}_2}{{\left(2\pi \right)}^{3}2\sqrt{m_2^2+p_2^2}}\frac{{\text{d}}^3{p}_3}{{\left(2\pi \right)}^{3}2\sqrt{m_3^2+p_3^2}}{\left(2\pi \right)}^4{\delta }^4\left(k-p_1-p_2-p_3\right)$

we choose $\stackrel{\to }{k}=0$ , $k^0=m$ , i.e. ${\stackrel{\to }{p}}_3=-\left({\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)$

$s_1={\left(k-p_1\right)}^2={\left(m-E_1\right)}^2-{\stackrel{\to }{p}}_1^2={\left(m-E_1\right)}^2-\left(E_1^2-m_1^2\right)=m^2+m_1^2-2m{E}_1$

$s_2={\left(m-E_2\right)}^2-{\stackrel{\to }{p}}_2^2=m^2+m_1^2-2m{E}_2$

${\stackrel{\to }{p}}_1^2=E_1^2-m_1^2$ , ${\stackrel{\to }{p}}_2^2=E_2^2-m_1^2$

${\stackrel{\to }{p}}_2^2={\stackrel{\to }{p}}_1^2+{\stackrel{\to }{p}}_2^2+2{\stackrel{\to }{p}}_1{\stackrel{\to }{p}}_2\cos {\theta }_{12}=E_1^2+E_2^2-2m_1^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_1^2}\cos {\theta }_{12}$ , $m=E_1+E_2+E_3$

$\begin{array}{c}{s}_3={\left(p_1+p_2\right)}^2={\left(m-\left(E_1+E_2\right)\right)}^2-{\left({\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)}^2\\ ={\left(m-\left(E_1+E_2\right)\right)}^2-\left(E_1^2+E_2^2-2m_1^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_1^2}\cos {\theta }_{12}\right)\end{array}$

$\begin{array}{c}{s}_3={\left(p_1+p_2\right)}^2\\ =2E_1{E}_2-2m\left(E_1+E_2\right)+m^2+2m_1^2-2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_1^2}\cos {\theta }_{12}\end{array}$

$E_1=\sqrt{m_1^2+{\stackrel{\to }{p}}_1^2}$ , $E_2=\sqrt{m_1^2+{\stackrel{\to }{p}}_2^2}$ ,

$E_3=\sqrt{m_1^2+{\left({\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)}^2}={\left(E_1^2+E_2^2-m_1^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_1^2}\cos {\theta }_{12}\right)}^{1/2}$

$x=\frac{s_2-s_1}{m_1^2}=\frac{2m\left(E_1-E_2\right)}{m_1^2}$

$y=\frac{s_3-s_0}{m_1^2}=\frac{2E_1{E}_2-2m\left(E_1+E_2\right)+2m^2/3+m_1^2-2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_1^2}\cos {\theta }_{12}}{m_1^2}$

We insert ${\left|M\left(k,p_1,p_2,p_3\right)\right|}^2=\frac{1}{8\pi }{\left|A_{++-}\left(x,y\right)\right|}^2$

and calculate Γ as an integral over $\left|p_1\right|=\left|{\stackrel{\to }{p}}_1\right|$ , $\left|p_2\right|=\left|{\stackrel{\to }{p}}_2\right|$ θ₁₂, integration ${\text{d}}^3{p}_3{\delta }^3\left({\stackrel{\to }{p}}_3+{\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)$ cancels out

$\text{d}\Gamma =\frac{{\left|A_{++-}\left(x,y\right)\right|}^2}{2m}\frac{4\pi \left(E_1^2-m_1^2\right)\text{d}\left|p_1\right|}{{\left(2\pi \right)}^{3}2E_1}\frac{2\pi \left(E_2^2-m_1^2\right)\text{d}\left|p_2\right|}{{\left(2\pi \right)}^{3}2E_2}\frac{1}{{\left(2\pi \right)}^{3}2E_3}{\left(2\pi \right)}^4\delta \left(m-E_1-E_2-E_3\right)$

and changing to E₁, E₂, θ₁₂: $\text{d}\left|p_1\right|=\frac{E_1\text{d}{E}_1}{\sqrt{E_1^2-m_1^2}}$ , $\text{d}\left|p_2\right|=\frac{E_2\text{d}{E}_2}{\sqrt{E_2^2-m_1^2}}$ ,

$\left|p_1\right|=\sqrt{E_1^2-m_1^2}$ , $\left|p_2\right|=\sqrt{E_2^2-m_1^2}$

$\begin{array}{c}\text{d}\Gamma =\frac{{\left|A_{++-}\left(x,y\right)\right|}^2}{8m{\left(2\pi \right)}^3}\sqrt{E_1^2-m_1^2}\text{d}{E}_1\sqrt{E_2^2-m_1^2}\text{d}{E}_2\\ \times \frac{\sin {\theta }_{12}\text{d}{\theta }_{12}}{{\left(E_1^2+E_2^2-2m_1^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_1^2}\cos {\theta }_{12}\right)}^{1/2}}\\ \times \delta \left(m-E_1-E_2-{\left(E_1^2+E_2^2-2m_1^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_1^2}\cos {\theta }_{12}\right)}^{1/2}\right)\end{array}$

we solve dΓ for E₂ [2] :

$E_2=\frac{-2E_1^{2}m-m^3-m{m}_1^2+E_1\left(3m^2+m_1^2\right)+\cos \left({\theta }_{12}\right){\left(\left(E_1^2-m_1^2\right)\left(\begin{array}{l}\left(m^2-m_1^2\right)\left(4E_1^2-4E_{1}m+m^2-m_1^2\right)\\ +4m_1^2\left(E_1^2-m_1^2\right)\cos {\left({\theta }_{12}\right)}^2\end{array}\right)\right)}^{1/2}}{-2{\left(E_1-m\right)}^2+2\left(E_1^2-m_1^2\right)\cos {\left({\theta }_{12}\right)}^2}$

and $m-E_1-E_2=\sqrt{E_1^2+E_2^2-m_1^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_1^2}\cos {\theta }_{12}}$

$\frac{{\left(m-\left(E_1+E_2\right)\right)}^2-E_1^2-E_2^2+m_1^2}{2\sqrt{E_1^2-m_1^2}\cos {\theta }_{12}}=\sqrt{E_2^2-m_1^2}$

now we carry out the integration over E₂ with the delta-function:

$\Gamma ={\displaystyle \int \frac{{\left|A_{++-}\left(x,y\right)\right|}^2}{8m{\left(2\pi \right)}^3}\text{d}{E}_1\frac{{\left(m-\left(E_1+E_2\right)\right)}^2-E_1^2-E_2^2+m_1^2}{2\cos {\theta }_{12}}\frac{\sin {\theta }_{12}\text{d}{\theta }_{12}}{m-\left(E_1+E_2\right)}}$

and after simplification

$\Gamma ={\displaystyle \int \frac{{\left|A_{++-}\left(x,y\right)\right|}^2}{8m{\left(2\pi \right)}^3}\frac{\sqrt{E_2^2-m_1^2}\sqrt{E_1^2-m_1^2}}{m-\left(E_1+E_2\right)}\sin {\theta }_{12}\text{d}{\theta }_{12}}\text{d}{E}_1$ (4)

The integration boundary in E₁ is $m_1\le E_1\le \left(1+f_{e1b1}\left(m,m_1,{\theta }_{12}\right)\right)m_1$ , in θ₁₂ $0\le {\theta }_{12}\le \pi$

where $f_{e1b1}\left(m,m_1,{\theta }_{12}\right)=\frac{\left|p_1\right|}{m{}_1}$ is the relative momentum, at which E₂ becomes

complex

$f_{e1b1}\left(m,m_1,{\theta }_{12}\right)=\frac{2m^3{m}_1-4m^2{m}_1^2-2m{m}_1^3+4m_1^4\sin {\left({\theta }_{12}\right)}^2-\sqrt{2}{\left(\begin{array}{l}{m}^2{m}_1^4\left(m^2\left(1-\cos \left(2{\theta }_{12}\right)\right)+2m_1^2+6m_1^4\cos \left(2{\theta }_{12}\right)\right)\\ +m_1^8\left(\cos \left(4{\theta }_{12}\right)-\cos \left(2{\theta }_{12}\right)\right)\end{array}\right)}^{1/2}}{4\left(m^2{m}_1^2-m_1^4\sin {\left({\theta }_{12}\right)}^2\right)}$

Numerical integration yields for $m_1=m\left({\pi }^{+}\right)=0.139\text{GeV}$ , $m=m\left(K^{+}\right)=0.493\text{GeV}$ [2] .

$\Gamma \left(m_1,m\right)=0.033\times {10}^{-16}\text{GeV}$ , the measured decay width is 0.0297 × 10⁻¹⁶ GeV (see below).

2.8. The General 3-Body Decay

We use the momentum notations $\Gamma \left(P_0\left(k,m\right)\to P\left(p_1,m_1\right)P\left(p_2,m_2\right)P\left(p_3,m_3\right)\right)$ [14] [18] .

We start again with Fermi’s golden rule:

$\text{d}\Gamma =\frac{{\left|M\left(k,p_1,p_2,p_3\right)\right|}^2}{2m}\frac{{\text{d}}^3{p}_1}{{\left(2\pi \right)}^{3}2E_1}\frac{{\text{d}}^3{p}_2}{{\left(2\pi \right)}^{3}2E_2}\frac{{\text{d}}^3{p}_3}{{\left(2\pi \right)}^{3}2E_3}{\left(2\pi \right)}^4{\delta }^4\left(k-p_1-p_2-p_3\right)$ (5)

we choose $\stackrel{\to }{k}=0$ , $k^0=m$ , i.e. ${\stackrel{\to }{p}}_3=-\left({\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)$

${\stackrel{\to }{p}}_1^2=E_1^2-m_1^2$ , ${\stackrel{\to }{p}}_2^2=E_2^2-m_2^2$

${\stackrel{\to }{p}}_3^2={\stackrel{\to }{p}}_1^2+{\stackrel{\to }{p}}_2^2+2{\stackrel{\to }{p}}_1{\stackrel{\to }{p}}_2\cos {\theta }_{12}=E_1^2+E_2^2-m_1^2-m_2^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_2^2}\cos {\theta }_{12}$ , $m=E_1+E_2+E_3$

$E_1=\sqrt{m_1^2+{\stackrel{\to }{p}}_1^2}$ , $E_2=\sqrt{m_2^2+{\stackrel{\to }{p}}_2^2}$ ,

$\begin{array}{c}{E}_3=\sqrt{m_3^2+{\left({\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)}^2}\\ ={\left(E_1^2+E_2^2+m_3^2-m_1^2-m_2^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_2^2}\cos {\theta }_{12}\right)}^{1/2}\end{array}$

now we calculate Γ as an integral over $\left|p_1\right|=\left|{\stackrel{\to }{p}}_1\right|$ , $\left|p_2\right|=\left|{\stackrel{\to }{p}}_2\right|$ θ₁₂, integration ${\text{d}}^3{p}_3{\delta }^3\left({\stackrel{\to }{p}}_3+{\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)$ cancels out

$\text{d}\Gamma =\frac{{\left|M\left(k,p_1,p_2,p_3\right)\right|}^2}{2m}\frac{4\pi \left(E_1^2-m_1^2\right)\text{d}\left|p_1\right|}{{\left(2\pi \right)}^{3}2E_1}\frac{2\pi \left(E_2^2-m_2^2\right)\text{d}\left|p_2\right|}{{\left(2\pi \right)}^{3}2E_2}\frac{1}{{\left(2\pi \right)}^{3}2E_3}{\left(2\pi \right)}^4\delta \left(m-E_1-E_2-E_3\right)$

and changing to E₁, E₂, θ₁₂: $\text{d}\left|p_1\right|=\frac{E_1\text{d}{E}_1}{\sqrt{E_1^2-m_1^2}}$ , $\text{d}\left|p_2\right|=\frac{E_2\text{d}{E}_2}{\sqrt{E_2^2-m_2^2}}$ ,

$\left|p_1\right|=\sqrt{E_1^2-m_1^2}$ , $\left|p_2\right|=\sqrt{E_2^2-m_2^2}$

$\begin{array}{c}\text{d}\Gamma =\frac{{\left|M\left(k,p_1,p_2,p_3\right)\right|}^2}{8m{\left(2\pi \right)}^3}\sqrt{E_1^2-m_1^2}\text{d}{E}_1\sqrt{E_2^2-m_2^2}\text{d}{E}_2\\ \times \frac{\sin {\theta }_{12}\text{d}{\theta }_{12}}{{\left(E_1^2+E_2^2+m_3^2-m_1^2-m_2^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_2^2}\cos {\theta }_{12}\right)}^{1/2}}\\ \times \delta \left(m-E_1-E_2-{\left(E_1^2+E_2^2+m_3^2-m_1^2-m_2^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_2^2}\cos {\theta }_{12}\right)}^{1/2}\right)\end{array}$

we solve for E₂ [2] :

$\begin{array}{c}{E}_2=(m\left(-2E_1^2-m^2-m_1^2+m_3^2\right)+E_1\left(3m^2+m_1^2+m_2^2-m_3^2\right)+\cos \left({\theta }_{12}\right)(m^4+2m^2{m}_1^2\stackrel{}{}\\ +m_1^4-2m^2{m}_2^2+m_2^4-2m^2{m}_3^2-2\left(m_1^2+m_2^2\right)m_3^2+m_3^4+2E_1^2\left(2m^2-m_2^2\right)\\ -4E_{1}m\left(m^2+m_1^2-m_2^2-m_3^2\right)+{2m_2^2\left(E_1^2-m_1^2\right)\cos \left(2{\theta }_{12}\right))}^{1/2})\\ /\left(-2{\left(E_1-m\right)}^2+2\left(E_1^2-m_1^2\right)\cos {\left({\theta }_{12}\right)}^2\right)\end{array}$

and $m-E_1-E_2={\left(E_1^2+E_2^2+m_3^2-m_1^2-m_2^2+2\sqrt{E_1^2-m_1^2}\sqrt{E_2^2-m_2^2}\cos {\theta }_{12}\right)}^{1/2}$

$\frac{{\left(m-\left(E_1+E_2\right)\right)}^2-E_1^2-E_2^2-m_3^2+m_1^2+m_2^2}{2\sqrt{E_1^2-m_1^2}\cos {\theta }_{12}}=\sqrt{E_2^2-m_2^2}$

now we carry out the integration over E₂ with the delta-function:

$\Gamma ={\displaystyle \int \frac{{\left|M\left(k,p_1,p_2,p_3\right)\right|}^2}{8m{\left(2\pi \right)}^3}\text{d}{E}_1\frac{{\left(m-\left(E_1+E_2\right)\right)}^2-E_1^2-E_2^2-m_3^2+m_1^2+m_2^2}{2\cos {\theta }_{12}}\frac{\sin {\theta }_{12}\text{d}{\theta }_{12}}{m-\left(E_1+E_2\right)}}$

and after simplification

$\Gamma ={\displaystyle \int \frac{{\left|M\left(k,p_1,p_2,p_3\right)\right|}^2}{8m{\left(2\pi \right)}^3}\frac{\sqrt{E_2^2-m_1^2}\sqrt{E_1^2-m_2^2}}{m-\left(E_1+E_2\right)}\sin {\theta }_{12}\text{d}{\theta }_{12}}\text{d}{E}_1$

setting $\left|M\left(k,p_1,p_2,p_3\right)\right|=1$ we obtain the partial kinematic factor for 3-body

decay $I_{\Gamma 3}\left(\frac{m_1}{m},\frac{m_2}{m},\frac{m_3}{m}\right)$

$\Gamma ={\displaystyle \int \frac{1}{8m{\left(2\pi \right)}^3}\frac{\sqrt{E_2^2-m_1^2}\sqrt{E_1^2-m_2^2}}{m-\left(E_1+E_2\right)}\sin {\theta }_{12}\text{d}{\theta }_{12}}\text{d}{E}_1=m{I}_{\Gamma 3}\left(m,m_1,m_2,m_3\right)$ (6)

The integration boundary in E₁ is $m_1\le E_1\le \left(1+f_{e1b1}\left(m,m_1,m_2,m_3,{\theta }_{12}\right)\right)m_1$ , in θ₁₂ $0\le {\theta }_{12}\le \pi$

where $f_{e1b1}\left(m,m_1,m_2,m_3,{\theta }_{12}\right)=\frac{\left|p_1\right|}{m{}_1}$ is the relative momentum, at which E₂

becomes complex

$\begin{array}{l}{f}_{e1b1}\left(m,m_1,m_2,m_3,{\theta }_{12}\right)\\ =(2\left(m^3{m}_1-2m^2{m}_1^2+m{m}_1^3-m{m}_1\left(m_2^2+m_3^2\right)+m_1^2{m}_2^2-m_1^2{m}_2^2\cos \left(2{\theta }_{12}\right)\right)\stackrel{}{}\\ -(-(m^2\left(m^2-4m{m}_1+6m_1^2-2m_2^2-2m_3^2\right)-4m{m}_1^3+m_1^4+4m{m}_1\left(m_2^2+m_3^2\right)\stackrel{}{}\end{array}$

$\begin{array}{l}-2m_1^2\left(m_2^2+m_3^2\right)+m_2^4+m_3^4-2m_2{}^2{m}_3{}^2)\left(4m^2{m}_1{}^2-2m_1^2{m}_2^2+2m_1^2{m}_2{}^2\cos \left(2{\theta }_{12}\right)\right)\\ +{4{\left(-m^3{m}_1+2m^2{m}_1^2-m{m}_1^3+m{m}_1\left(m_2^2+m_3^2\right)+m_1^2{m}_2^2\left(\cos \left(2{\theta }_{12}\right)-1\right)\right)}^2)}^{1/2})\\ /\left(2\left(2m^2{m}_1^2-m_1^2{m}_2^2+m_1^2{m}_2^2\cos \left(2{\theta }_{12}\right)\right)\right)\end{array}$ (6a)

The kinematic factor $I_{\Gamma 3}\left(m,m_1,m_2,m_3\right)$ can be calculated numerically.

The total kinematic factor results from $I_{\Gamma 3}\left(m,m_1,m_2,m_3\right)$ by symmetrization over all 6 index permutations

$I_{\Gamma 3s}\left(m,m_1,m_2,m_3\right)=\left(I_{\Gamma 3}\left(m,m_1,m_2,m_3\right)+I_{\Gamma 3}\left(m,m_1,m_3,m_2\right)+\cdots \right)/6$

Here is the plot of $I_{\Gamma 3s}\left(1,m_1,0.1,0.1\right){10}^6$ shown in Figure 7.

Example: $\Gamma \left(\mu \to e{\bar{\nu }}_e{\nu }_{\mu }\right)$ with kinematic factor: $I_{\Gamma 3s}\left(m\left(\mu \right),m\left(e\right),0,0\right)=0.3835$ .

2.9. The General 2-Body Decay

We use the momentum notations $\Gamma \left(P_0\left(k,m\right)\to P\left(p_1,m_1\right)P\left(p_2,m_2\right)\right)$ [14] [18] .

We start again with Fermi’s golden rule for 2-body decay [11] :

$\text{d}\Gamma =m\frac{{\left|M\left(k,p_1,p_2\right)\right|}^2}{2}\frac{{\text{d}}^3{p}_1}{{\left(2\pi \right)}^{3}2E_1}\frac{{\text{d}}^3{p}_2}{{\left(2\pi \right)}^{3}2E_2}{\left(2\pi \right)}^4{\delta }^4\left(k-p_1-p_2\right)$ (7)

we choose $\stackrel{\to }{k}=0$ , $k^0=m$ , i.e. ${\stackrel{\to }{p}}_2=-{\stackrel{\to }{p}}_1$

${\stackrel{\to }{p}}_1^2=E_1^2-m_1^2$ , ${\stackrel{\to }{p}}_2^2=E_2^2-m_2^2$

$m=E_1+E_2$

$E_1=\sqrt{m_1^2+{\stackrel{\to }{p}}_1^2}$ , $E_2=\sqrt{m_2^2+{\stackrel{\to }{p}}_1^2}=\sqrt{E_1^2+m_2^2-m_1^2}=m-E_1$ , ${\delta }^4\left(k-p_1-p_2\right)=\delta \left(m-E_1-E_2\right){\delta }^3\left({\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)$

Figure 7. Plot of $I_{\Gamma 3s}\left(1,m_1,0.1,0.1\right){10}^6$ .

now we calculate Γ as an integral over $\left|p_1\right|=\left|{\stackrel{\to }{p}}_1\right|$ , integration ${\text{d}}^3{p}_2{\delta }^3\left({\stackrel{\to }{p}}_1+{\stackrel{\to }{p}}_2\right)$ cancels out

and changing to $E_1$ : $\text{d}\left|p_1\right|=\frac{E_1\text{d}{E}_1}{\sqrt{E_1^2-m_1^2}}$ , $\left|p_1\right|=\sqrt{E_1^2-m_1^2}$

$\text{d}\Gamma =m\frac{{\left|M\left(k,p_1,p_2\right)\right|}^2}{8{\left(2\pi \right)}^2}\frac{4\pi \sqrt{E_1^2-m_1^2}\text{d}{E}_1}{\sqrt{E_1^2+m_2^2-m_1^2}}\delta \left(m-E_1-E_2\right)$

from $\sqrt{E_1^2+m_2^2-m_1^2}=m-E_1$ we obtain the solution [2]

$E_{10}=\frac{m^2+m_1^2-m_2^2}{2m}$ ,

the integration $\text{d}{E}_1\delta \left(m-E_1-E_2\right)$ cancels out and we obtain, setting $\left|M\left(k,p_1,p_2,p_3\right)\right|=1$

$\begin{array}{c}\Gamma =\frac{m}{4\left(2\pi \right)}\frac{\sqrt{E_{10}^2-m_1^2}}{\sqrt{E_{10}^2+m_2^2-m_1^2}}\\ =\frac{1}{8m\pi }\frac{{\left(m^4+m_1^4+m_2^4-2m^2{m}_1^2-2m^2{m}_2^2-2m_1^2{m}_2^2\right)}^{1/2}}{{\left(m^4+m_1^4+m_2^4-2m^2{m}_1^2+2m^2{m}_2^2-2m_1^2{m}_2^2\right)}^{1/2}}\end{array}$ (8)

we obtain the kinematic factor for 2-body decay $I_{\Gamma 2}\left(m,m_1\right)$

$I_{\Gamma 2}\left(m,m_1,m_2\right)=\frac{\Gamma }{m}=\frac{1}{8\pi }\frac{{\left(m^4+m_1^4+m_2^4-2m^2{m}_1^2-2m^2{m}_2^2-2m_1^2{m}_2^2\right)}^{1/2}}{{\left(m^4+m_1^4+m_2^4-2m^2{m}_1^2+2m^2{m}_2^2-2m_1^2{m}_2^2\right)}^{1/2}}$ (8a)

The total kinematic factor for 2-body decay results from the symmetrized $I_{\Gamma 2}\left(m,m_1\right)$

$I_{\Gamma 2s}\left(m,m_1,m_2\right)=\frac{I_{\Gamma 2}\left(m,m_1\right)+I_{\Gamma 2}\left(m,m_2\right)}{2}$

As an example, here is the plot $I_{\Gamma 2s}\left(1,m_1,0.5\right)$ shown in Figure 8.

Example: $\Gamma \left(\pi \to \mu \nu \right)$ , with kinematic factor: $I_{\Gamma 2s}\left(m\left(\pi \right),m\left(\mu \right),0\right)=0.0251$ .

Figure 8. Plot of $I_{\Gamma 2s}\left(1,m_1,0.5\right)$ .

3. The Theoretical Background and the Phenomenological Decay Formula

Schematics: decay width phenomenological formula, interaction energy

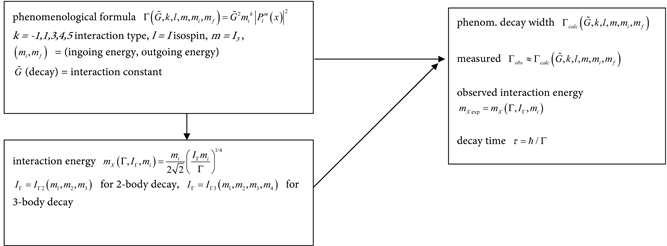
In this chapter, we follow the following scheme underlying the phenomenological formula by Chang [1] for decay width, the derived interaction energy, and resulting decay time.

The phenomenological formula is a semi-empirical scheme for the calculation of the decay width Γ of a decay: ${\Gamma }_{calc}\left(\tilde{G},k,l,m,m_i,m_f\right)={\tilde{G}}^2{m}_i^k{\left|P_l{}^m\left(x\right)\right|}^2$ , depending on $\left(m_i,m_f\right)$ = (ingoing energy, outgoing energy), interaction constant (decay dependent) $\tilde{G}$ , interaction type k = −1, 1, 3, 4, 5, and extended isospin I with the traditional notations l = I, m = I₃.

From the decay width, the decay time follows immediately $\tau =\hslash /\Gamma$ .

The agreement between the phenomenological ${\Gamma }_{calc}$ and the observed values ${\Gamma }_{obs}$ is remarkably good (see chap. 6).

The interaction energy $m_X\left(\Gamma ,I_{\Gamma },m_i\right)$ between the incoming and the outgoing state in the process (corresponding to the energy of the mediating particle in the Feynman diagram, e.g. $W^{-}$ boson in the neutron decay), can be calculated from Γ using kinematics factors $I_{\Gamma }\left(m_1,m_2,\cdots \right)$ .

The kinematics factors describe the statistics of the process and depend on the involved particle masses.

In 1.8 and 1.9 we calculated the kinematic factor and obtained for decay width the general formula $\Gamma ={\left|M\right|}^2{I}_{\Gamma }{m}_i$ .

The formula for interaction energy $m_X\left(\Gamma ,I_{\Gamma },m_i\right)=\frac{m_i}{2\sqrt{2}}{\left(\frac{I_{\Gamma }{m}_i}{\Gamma }\right)}^{1/4}$ is derived

below in chap. 3.1.

3.1. The Phenomenological Decay Formula and Interaction Energy

The phenomenological decay formula

The phenomenological formula for the decay width is [1]

$\Gamma ={\tilde{G}}^2{m}_i^k{\left|P_l^m\left(x\right)\right|}^2=\frac{G^2}{C_1}{m}_i^k{\left|P_l^m\left(x\right)\right|}^2$ (9)

where $P_l^m\left(x\right)$ Legendre polynomial $m=l$ or $m=l+\text{1}$ , l = isospin I, $x=\frac{m_f}{m_i}$ mass ratio, $\tilde{G}=\frac{G}{\sqrt{C_1}}$ with G = interaction constant, $m_i$ is the initial mass.

The constant C₁ is process-dependent, standard value $C_1=4\pi$ , with exceptions for muon: $C_1=192{\pi }^3$ , and for neutron: $C_1=2{\pi }^3$ .

The G constants are: for kaons $G^2=g_1^2=2.06\times {10}^{-14}$ , for pions $G^2=g_0^2=2.18\times {10}^{-14}$ , for leptonic decays $A\to A^{\prime }e{\bar{\nu }}_e\left(\Delta S=0\right)$

$G=G_l=1.02\times {10}^{-5}\left(\frac{1}{m_p^2}\right)=1.16\times {10}^{-5}{\text{GeV}}^{-2}$ , for hyperons

$G=g_{h1}=5.81\times {10}^{-7}\text{GeV}$ or $G=g_{h2}=1.4\times {10}^{-8}{\text{GeV}}^{-3/2}$ .

The interaction constants for hyperons in [1] were given by

$G=g_h=6.2\times {10}^{-7}\left(\frac{m_p}{m_i}\right)$ or $G=g_{h\text{'}}=1.28\times {10}^{-8}{\left(\frac{m_i}{m_p}\right)}^{3/2}$ , they have been corrected, since G must not depend on initial mass $m_i$ , also the power coefficient k

and the data tables were corrected accordingly.

The power coefficient is

k = 1 for a dimensionless $\tilde{G}$ , like in pion decay

$\Gamma \left(\pi \to \mu {\nu }_{\mu }\right)={\tilde{G}}^2{m}_i{x}^2{\left(1-x^2\right)}^2=\frac{G^2{m}_i}{4\pi }{x}^2{\left(1-x^2\right)}^2$ , $G^2=g_0^2=2.18\times {10}^{-14}$

k = 5 for a dimensional $\tilde{G}$ , $\left[\tilde{G}\right]={\text{GeV}}^{-2}$ , like in muon decay

$\Gamma \left(\mu \to e{\nu }_e{\nu }_{\mu }\right)={\tilde{G}}^2{m}_i^5{\left(1-x^2\right)}^4=\frac{G_F^2{m}_i^5}{192{\pi }^3}{\left(1-x^2\right)}^4$

k = 3 for a dimensional $\tilde{G}$ , $\left[\tilde{G}\right]={\text{GeV}}^{-1}$ , like in π⁰ decay $\Gamma \left({\pi }^0\to \gamma \gamma \right)={\tilde{G}}^2{m}_i^3{\left(1-x^2\right)}^3$

k = −1 for a dimensional $\tilde{G}$ , $\left[\tilde{G}\right]=\text{GeV}$ , for kaon decays with $\tilde{G}\cong g_{h1}$

k = 4 for a dimensional $\tilde{G}$ , $\left[\tilde{G}\right]={\text{GeV}}^{-3/2}$ , for non-kaon hyperon decays with $\tilde{G}\cong g_{h2}$

so in all cases $\left[\Gamma \right]=\text{m}$ , i.e. the dimension is energy, as it must be.

The extended isospin I [5] [19] includes higher generation quarks, $I\left(s\right)=I\left(c\right)=1/2$ and $I\left(l\right)=1$ for leptons l as well as $I\left(\gamma \right)=1$ for the photon.

The extended isospin has the following values shown in Table 4.

The angular momentum in decay width: $l=\left|\Delta I\right|=\left|I_i\pm I_f\right|$ is the difference or sum of the initial and final isospin.

The interaction energy

The interaction energy m_X is the (excitation) energy of the mediating virtual exchange boson (for pure weak decays: W or Z-boson).

We can deduce the interaction energy from the phenomenological formula in

Table 4. Extended isospin.

the following way.

We consider the phenomenological formula for k = 5 (e.g. muon decay) in the

form $\Gamma ={\tilde{G}}^2{m}_i^5{\left(1-x^2\right)}^4$ , where $x=\frac{m_f}{m_i}$ .

We separate the kinematic factor as in chap. 2.8 and 2.9 in the form $\Gamma ={\left|M\right|}^2{I}_{\Gamma }{m}_i$ .

So we conclude $I_{\Gamma }={\left(1-x^2\right)}^4$ , $M^2={\tilde{G}}^2{m}_i^4$ .

In analogy to the weak interaction mediated by the W-boson (as in muon

decay chap.3.3) $\tilde{G}=\frac{G_F}{\sqrt{2}}=\frac{g^2}{8M_W^2}$ (g weak interaction constant), we make the

ansatz for the matrix element M and the interaction energy m_X

$M=\frac{m_i^2}{8m_X^2}$

The decay width with the matrix element M and the kinematic $I_{\Gamma }$ factor becomes then

$\Gamma ={\left|M\right|}^2{I}_{\Gamma }{m}_i={\left(\frac{m_i^2}{8m_X^2}\right)}^2{I}_{\Gamma }{m}_i$ or in general $\frac{m_X}{m_i}=f_I{\left(\frac{m_i}{\Gamma }\right)}^{1/4}$ , where $f_I=\frac{I_{\Gamma }^{1/4}}{2\sqrt{2}}$ .

From this formula we can derive a general semi-empirical formula for the interaction energy m_X, where the kinematic factor is dimensionless $\left[I_{\Gamma }\right]=1$ ,

$m_X=\frac{m_i}{2\sqrt{2}}{\left(\frac{I_{\Gamma }{m}_i}{\Gamma }\right)}^{1/4}$ (10)

where $I_{\Gamma }=I_{\Gamma 2}\left(m_1,m_2,m_3\right)$ for 2-body decay,

$I_{\Gamma }=I_{\Gamma 3}\left(m_1,m_2,m_3,m_4\right)$ for 3-body decay (see 1.8, 1.9)

For k = 1 $\frac{m_i^4}{m_X^4}=\frac{64{\tilde{G}}^2}{I_{\Gamma }}{\left|P_l^m\left(x\right)\right|}^2$ with the phenomenological formula

$\Gamma ={\tilde{G}}^2{m}_i{\left|P_l^m\left(x\right)\right|}^2$ (10a)

For k = 5 $\frac{1}{m_X^4}=\frac{64{\tilde{G}}^2}{I_{\Gamma }}{\left|P_l^m\left(x\right)\right|}^2$ with $\Gamma ={\tilde{G}}^2{m}_i^5{\left(1-x^2\right)}^4=\frac{G_F^2{m}_i^5}{192{\pi }^3}{\left(1-x^2\right)}^4$

(10b)

For k = 3 $\frac{1}{m_X^2}=\frac{64{\tilde{G}}^2}{I_{\Gamma }}{\left|P_l^m\left(x\right)\right|}^2$ with $\Gamma ={\tilde{G}}^2{m}_i^3{\left(1-x^2\right)}^3$ (10c)

3.2. Derivation of Angular Momentum Dependence in the Phenomenological Formula

Laplace operators in spherical coordinates reads [1]

$\Delta \psi =\frac{1}{r^2}\left(\frac{\partial }{\partial r}\left(r^2\frac{\partial \psi }{\partial p}\right)+\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial \psi }{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^2\psi }{\partial {\phi }^2}\right)$

quantum kinetic energy is $E_{kin}\left(\psi \right)=-\frac{{\hslash }^2\Delta \psi }{2m}$

with the ansatz $\psi =R\left(r\right)\Theta \left(\theta ,\phi \right)$

for rigid rotator r=const and we obtain the angular momentum spectrum

$\frac{1}{\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial \psi }{\partial \theta }\right)+\frac{1}{{\sin }^2\theta }\frac{{\partial }^2\psi }{\partial {\phi }^2}=l\left(l+1\right)$ with kinetic energy $E_{kin}=\frac{L^2}{2I}=\frac{h^{2}l\left(l+1\right)}{8{\pi }^{2}I}$

where l is the angular momentum quantum number

with eigenfunctions

${\psi }_{lm}=N_{lm}{P}_l^{\left|m\right|}\left(\cos \theta \right)\exp \left(im\phi \right)$ , ${\left|{\psi }_{lm}\right|}^2=\frac{1}{4\pi }\frac{\left(l-\left|m\right|\right)\text{!}}{\left(l+\left|m\right|\right)\text{!}}\left(2l+1\right)P_l^{\left|m\right|}{\left(\cos \theta \right)}^2$

and decay width $\Gamma =A{\left|{\psi }_{lm}\right|}^2=\frac{A}{4\pi }\frac{\left(l-\left|m\right|\right)\text{!}}{\left(l+\left|m\right|\right)\text{!}}\left(2l+1\right)P_l^{\left|m\right|}{\left(\cos \theta \right)}^2$

with $x=\cos \theta =\frac{p_z}{\left|\stackrel{\to }{p}\right|}$ and $x=\frac{{\displaystyle \sum m_f}}{m_i}$ , $m=l$ or $m=l-\text{1}$

Legendre functions $P_l^m\left(x\right)=\frac{1}{\Gamma \left(1-m\right)}{\left(\frac{1+x}{1-x}\right)}^{m/2}{}_{2}F{}_1\left(-l,l+1;1-m;\frac{1-x}{2}\right)$

with hypergeometric function ${}_{2}F{}_1$

associated Legendre polynomials

$P_l^m\left(x\right)={\left(-1\right)}^m{2}^l{\left(1-x^2\right)}^{m/2}{\displaystyle \underset{k=m}{\overset{l}{\sum }}\frac{k!}{\left(k-m\right)!}{x}^{k-m}\left(\begin{array}{c}l\\ k\end{array}\right)\left(\begin{array}{c}\left(l+k-1\right)/2\\ l\end{array}\right)}$

$P_{l+1}^l\left(x\right)=x\left(2l+1\right)P_l^l\left(x\right)$ , $P_l^l\left(x\right)={\left(-1\right)}^l\left(2l-1\right)!!{\left(1-x^2\right)}^{1/2}$ , $P_{l+1}^{l+1}\left(x\right)=-\left(2l+1\right)\sqrt{1-x^2}{P}_l^l(\; x\; )$

$P_0^0\left(x\right)=1$ , $P_1^0\left(x\right)=x$ , $P_1^{-1}\left(x\right)=\frac{1}{2}{\left(1-x^2\right)}^{1/2}$ , $P_1^1\left(x\right)=-{\left(1-x^2\right)}^{1/2}$ ,

$P_2^0\left(x\right)=\frac{1}{2}\left(3x^2-1\right)$

and the decay width becomes ${\Gamma }_{l,\alpha }\left(x\right)=C{x}^{2\left(\alpha -1\right)}{\left(1-x^2\right)}^l$ , $\alpha =1,2$

In the following, the angular momentum L is replaced by the isospin I.

3.3. Muon Decay Theory

The analytical formula from the Feynman diagram is

$\Gamma \left(\mu \to e{\nu }_e{\nu }_{\mu }\right)=\frac{G_F^2{m}_{\mu }^5}{192{\pi }^3}$ [6] , G_F Fermi-constant (11)

exact formula with corrections [10]

$\Gamma \left(\mu \to e{\bar{\nu }}_e{\nu }_{\mu }\right)=\frac{G_F^2{m}_{\mu }^5}{192{\pi }^3}f\left(\frac{m_e^2}{m_{\mu }^2}\right)\left(1+f_{rc}\left(\frac{\alpha }{\pi }\right)\right)\left(1+\frac{3}{5}\frac{m_{\mu }^2}{m_W^2}+\cdots \right)$ (11a)

$f_{rc}\left(x\right)=\frac{x}{2}\left(\frac{25}{4}-{\pi }^2\right)\left(1+x\left(\frac{2}{3}\log \frac{m_{\mu }}{m_e}-3.7\right)+x^2\left(\frac{4}{9}{\log }^2\frac{m_{\mu }}{m_e}-2\log \frac{m_{\mu }}{m_e}+C\right)+\cdots \right)$ (11b)

and the phenomenological formula

$\Gamma \left(\mu \to e{\nu }_e{\nu }_{\mu }\right)=\frac{G_F^2{m}_{\mu }^5}{192{\pi }^3}{\left(1-\frac{m_e^2}{m_{\mu }^2}\right)}^4=\frac{G_F^2{m}_{\mu }^5}{192{\pi }^3}{\left(1-x^2\right)}^4$ [1] , $l=4$ (11c)

This is the general formula for a leptonic weak 3-body decay, setting initial mass $m_i=m_{\mu }$ .

The (charged) weak interaction in the Feynman-Gell-Mann form reads

$H_{weak}=\frac{G_F}{\sqrt{2}}{J}^{\mu }{J}_{\mu }^{†}$ [6] (9.1), where J_μ is the charged leptonic-hadronic current

$J_{\mu }=L_{\mu }+H_{\mu }$ and $L_{\mu }\left(x\right)=2{\bar{e}}_L\left(x\right){\gamma }_{\mu }{\nu }_e\left(x\right)+\cdots$ is the leptonic current,

$H_{\mu }\left(x\right)=2{\bar{u}}_L\left(x\right){\gamma }_{\mu }{d}_L\left(x\right)+\cdots$ is the analogous hadronic current.

In the standard model, the (charged) weak interaction is mediated by the massive W-boson W_μ with mass M_W for the charged current, with the Lagrangian

$L_{weak}=-\frac{g}{2\sqrt{2}}\left(J^{\mu }{\bar{W}}_{\mu }+W^{\mu }{\bar{J}}_{\mu }\right)$ (12)

where the effective interaction constant is $G=\frac{G_F}{\sqrt{2}}=\frac{g^2}{8m_W^2}$ .

We can use the total current and use an excited intermediate W-boson, which includes the hadronic part, with the total mass m_X > M_W and calculate it from

the effective measured coupling constant $G=\frac{G_F}{\sqrt{2}}$ , setting g = 1:

$G^2=\frac{1}{64m_X^4}$

The isospin numbers are $l=\Delta I=I_f+I_i=3+1=4$ and $m=l=4$ .

3.4. Pion Decay Theory

The analytical formula from the Feynman diagram is

$\Gamma \left(\pi \to \mu {\nu }_{\mu }\right)=\frac{G_F^2{m}_{\pi }}{8\pi }{f}_{\pi }^2{V}_{ud}^2{m}_{\mu }^2{\left(1-\frac{m_{\mu }^2}{m_{\pi }^2}\right)}^2\approx \frac{G_F^2{m}_{\pi }^5}{8\pi }\frac{m_{\mu }^2}{m_{\pi }^2}{\left(1-\frac{m_{\mu }^2}{m_{\pi }^2}\right)}^2$ [ [11] , (13.26)] (13)

G_F Fermi-constant, and the phenomenological formula

$\Gamma \left(\pi \to \mu {\nu }_{\mu }\right)=\frac{G^2{m}_{\pi }}{4\pi }\frac{m_{\mu }^2}{m_{\pi }^2}{\left(1-\frac{m_{\mu }^2}{m_{\pi }^2}\right)}^2=\frac{G^2{m}_{\pi }}{4\pi }{x}^2{\left(1-x^2\right)}^2$ [1] (13a)

The (charged) weak interaction has the form

$H_{weak}=\frac{G_F}{\sqrt{2}}{J}^{\lambda }\left(\mu ,{\nu }_{\mu }\right)J_{\lambda }\left(u,d\right)$ with the leptonic current

$J^{\lambda }\left(\mu ,{\nu }_{\mu }\right)=\bar{\mu }{\gamma }^{\lambda }\left(1-{\gamma }_5\right)\nu$ and the hadronic current $J^{\lambda }\left(u,d\right)=\bar{u}{\gamma }^{\lambda }d$ for ${\pi }^{-}=\bar{u}d$ ( [6] , (13.6)).

Using the same procedure as above with the excited intermediate W-boson, we calculate M_X from the above two formulas:

$\frac{G_F^2}{8\pi }{\left(\frac{m_{\pi }}{m_X}\right)}^4=\frac{G^2}{4\pi }$ and $\frac{G_F}{\sqrt{2}}=\frac{g_F^2}{8M_X^2}$

and setting g_F = 1 and initial mass $m_i=m_{\pi }$

we obtain ${\left(\frac{m_i}{m_X}\right)}^4=64G^2$ .

The isospin numbers are $l=\Delta I=I_f+I_i=2+1=3$ and $m=l-1=2$ .

3.5. Kaon Pion Decay Theory

The kaon-pion decay is shown in Figure 9.

The generalized and isospin-adapted 3-body semi-leptonic formula (from the muon) decay is

$\Gamma \left(K^{\pm }\to {\pi }^{\pm }{\pi }^{+}{\pi }^{-}\right)=\frac{g^4{m}_i}{32\times 192{\pi }^3}\left(\frac{m_i^4}{m_X^4}\right){\left(1-\frac{m_f^2}{m_i^2}\right)}^4$ (14)

and the phenomenological formula

$\Gamma \left(K^{\pm }\to {\pi }^{\pm }{\pi }^{+}{\pi }^{-}\right)=\frac{G^2{m}_{K+}}{4\pi }{\left(1-\frac{m_{\pi }^2}{m_{K+}^2}\right)}^2$ [1] , where $G=2g_1\sqrt{\alpha }$ (14a)

From these two formulas setting g = 1 we obtain for m_x:

$\frac{m_i^4}{m_X^4}=8\times 192{\pi }^2{G}^2=32\times 192{\pi }^2{g}_1^2\alpha$

The interaction is mediated by W-boson and a gluon: it is a weak-hadronic transformation.

Figure 9. Kaon decay.

The isospin numbers are $l=\Delta I=I_f-I_i=3-1=2$ and $m=l=2$ .

3.6. Neutron Decay Theory

The quark process of the neutron decay is shown in Figure 10.

The analytical formula from the Feynman diagram is [8]

$\Gamma \left(n\to pe{\nu }_e\right)=\left(G_V^2+3G_A^2\right)\frac{m_e^5}{2{\pi }^3}{f}_R=G_F^2{V}_{ud}^2\left(1+3{\lambda }^2\right)\frac{m_e^5}{2{\pi }^3}{f}_R$ (15)

$G_V=G_F{V}_{ud}$ , $G_A=G_F{V}_{ud}\lambda$ , $\lambda =1.255$ , $V_{ud}=0.974$ , $G_F=1.166\times {10}^{-5}{\text{GeV}}^{-1}$

with the phase-space term [9]

$f_R=\frac{1}{60}\left(2{\xi }^4-9{\xi }^2-8\right)\sqrt{{\xi }^2-1}+\frac{1}{4}\xi \log \left(\xi +\sqrt{{\xi }^2-1}\right)$ with $\xi \equiv \frac{m_n-m_p}{m_e}=2.53$ ,

so $f_R=1.6332$

and the phenomenological formula for decay width is

$\Gamma \left(n\to pe{\nu }_e\right)=G^2{m}_i^5{\left(1-\frac{m_f^2}{m_i^2}\right)}^4$ [1] , $l=4$ (15a)

with initial mass $m_i=m_n$ and final mass $m_f=m_p+m_e$ and obtain with the same ansatz as for $\Gamma \left(\mu \to e{\nu }_e{\nu }_{\mu }\right)$ :

$G^2=\frac{1}{192{\pi }^{3}32M_X^4}$

The neutron decay involves in fact only 2 quarks $\Gamma \left(n\to pe{\nu }_e\right)=\Gamma \left(dd\to ude{\nu }_e\right)$

so the isospin numbers are $l=\Delta I=I_f+I_i=3+1=4$ and $m=l=4$ with $I_f=I\left(ud\right)+I\left(e\right)+I\left(\nu \right)=1+1+1=3$ and $I_i=I\left(dd\right)=1$ .

3.7. Theory of 3-Body Eta-Pion Decay

The eta-pion decay is shown in Figure 11.

The generalized and isospin-adapted 3-body semi-leptonic formula (from the muon) decay is

Figure 10. Neutron decay.

Figure 11. Eta-pion decay.

$\Gamma \left(\eta \to {\pi }^0{\pi }^{+}{\pi }^{-}\right)=\frac{g^4{m}_i}{32\times 192{\pi }^3}\left(\frac{m_i^4}{m_X^4}\right){\left(1-\frac{m_f^2}{m_i^2}\right)}^4$ (16)

and the phenomenological formula [1]

$\Gamma \left(\eta \to {\pi }^0{\pi }^{+}{\pi }^{-}\right)=\frac{G^2}{4\pi }{m}_i{\left(1-\frac{m_f^2}{m_i^2}\right)}^4$ (16a)

From this setting g = 1 we obtain for m_x:

$\frac{m_i^4}{m_X^4}=8\times 192{\pi }^2{G}^2$

The decay is mainly hadronic, but the kinematics is one of a 3-body decay, so we can use the generalized 3-body semi-leptonic formula from above.

The intermediate boson here is ${\pi }^0$ , so $m_X\propto m\left({\pi }^0\right)$ and the isospin numbers are $l=\Delta I=I_f+I_i=3+1=4$ and $m=l=4$ .

3.8. Theory of 2-Photon Meson Decay

The formula for the radiative 2-photon meson decay is:

$\Gamma \left({\pi }^0\to \gamma \gamma \right)=\frac{{\alpha }^2{m}_i^3}{64{\pi }^3{m}_X^2}$ (17)

where $m_i=m\left({\pi }^0\right)$ and $m_X=F_{\pi }$ , $F_{\pi }=\frac{2m_u}{\sqrt{Z_{\pi }}}$ pseudoscalar weak decay constant [20] .

the phenomenological formula is

$\Gamma \left({\pi }^0\to \gamma \gamma \right)=\frac{G^2{m}_i^3}{4\pi }{\left(1-\frac{m_f^2}{m_i^2}\right)}^3$ (17a)

From this we obtain for m_x: $m_X=\frac{4\pi \alpha }{G}$ .

The intermediate boson here is the strongly excited ${\pi }^0$ , so $m_X\propto 10m\left({\pi }^0\right)$ and the isospin numbers are $l=\Delta I=I_f+I_i=2+1=3$ and $m=l=3$ .

3.9. Theory of 1-Photon Hyperon Decay

The photon hyperon decay is shown in Figure 12.

The interaction becomes for the transition $s\to d\gamma$

$H_{sd\gamma }=\bar{d}{\sigma }_{\mu \nu }\left(a+b\gamma {}_5\right)s{q}^{\mu }{A}^{\nu }\alpha$ , where $A^{\nu }$ , $q^{\mu }$ are the photon and its momentum.

Figure 12. Photon hyperon decay.

For the analytical formula we can use the extended isospin-adapted expression from the pion decay (here $\Gamma \left({\Sigma }^{+}\to p\gamma \right)$ )

$\frac{G_F^2{m}_{\pi }^5}{8\pi }\frac{m_{\mu }^2}{m_{\pi }^2}{\left(1-\frac{m_{\mu }^2}{m_{\pi }^2}\right)}^2$

$\Gamma \left({\Sigma }^{+}\to p\gamma \right)=f_{\pi }\frac{G_F^2{\alpha }^2{m}_i^5}{8\pi }{\left(1-\frac{m_f^2}{m_i^2}\right)}^2$ (18)

where $m_i=m\left({\Sigma }^{+}\right)$ and $m_f=m\left(p\right)$ , $f_{\pi }$ is the hadronic correction factor the phenomenological formula is

$\Gamma \left({\Sigma }^{+}\to p\gamma \right)=\frac{G^2{m}_i^5}{4\pi }{\left(1-\frac{m_f^2}{m_i^2}\right)}^2$ (18a)

From this we obtain for m_x: $m_X^4=\frac{{\alpha }^2}{64G^2}$ or $m_X=\sqrt{\frac{\alpha }{8G}}$

and the isospin numbers are $l=\Delta I=I_f+I_i=\left(1/2+1\right)+1/2=2$ and $m=l=2$ .

3.10. The Generalized Weak Decay Formula

We have seen in 2.3 for the muon decay that the decay interaction has the Feynman-Gell-Mann form

$H_{weak}=\frac{G_F}{\sqrt{2}}{\bar{J}}^{\mu }{J}_{\mu }$ where $G_F/\sqrt{2}=g^2/\left(8M_W^2\right)$

or in generalized form (in natural units)

$H_{\mathrm{int}}=\frac{g^2}{8m_X^2}{\bar{J}}_1^{\mu }{\left(J_2\right)}_{\mu }$ (19)

where g is the (dimensionless) interaction constant, m_X is the interaction energy (excitation energy of the intermediate boson), J₁ and J₂ are the currents involved, e.g. the lepton current ${\left(J_2\right)}_{\mu }=\bar{e}\left(x\right){\gamma }_{\mu }\left(1-{\gamma }_5\right){\nu }_e\left(x\right)$ .

The current has dimension length-³, so the formula in cgs units reads

$H_{\mathrm{int}}={\left(\hslash c\right)}^3\frac{g^2}{8m_X^2}{\bar{J}}_1^{\mu }{\left(J_2\right)}_{\mu }$ , so H_int has dimension energy/length³, i.e. energy

density, as it should be.

The decay width (energy) becomes then

$\Gamma ={\displaystyle \int H_{\mathrm{int}}\left(x\right){\text{d}}^{3}x}$ (19a)

4. Particle Data

In the following Table 5 we present the data for the particles involved in the decays [6] [19] [21] .

Table 5. Particle data.

5. Decay Width and Interaction Energy for Different Types of Decays

In this chapter, we compare the observed decay bandwidths with the ones calculated from the semi-empirical formula. As we shall see, there is in general a satisfactory agreement between the observed and the calculated values [1] [22] .

Here, m_X is calculated according to the formula in 2.1 from the observed decay width Γ_obs

$m_X=\frac{m_i}{2\sqrt{2}}{\left(\frac{I_{\Gamma }{m}_i}{{\Gamma }_{obs}}\right)}^{1/4}$ (20)

5.1. Strange Hyperon Decays with Pions

Here we have [23]

$\Gamma =C{\left|{\psi }_{1,1}\right|}^2=\frac{G^2}{4\pi }{m}_i^{-1}\left(1-x^2\right)$ , $\left|\Delta S\right|=1$ , $l=\Delta I=1$ , $m=1$ , $x=\frac{m_f}{m_i}$ , $k=-1$

with $g_{h1}=5.81\times {10}^{-7}\text{GeV}$

$\Lambda \to p{\pi }^{-}$ , $\Lambda \to n{\pi }^0$ , $G=g_{h1}$ resp. $G=g_{h1}/\sqrt{2}$

${\Sigma }^{+}\to p{\pi }^0$ , ${\Sigma }^{+}\to n{\pi }^{+}$ , ${\Sigma }^{-}\to n{\pi }^{-}$ , $G=g_{h1}$

${\Xi }^0\to \Lambda {\pi }^0$ , ${\Xi }^{-}\to \Lambda {\pi }^{-}$ , $G=g_{h1}$ resp. $G=g_{h1}/\sqrt{2}$

The data for the strange hyperon decays with pions are shown in Table 6.

The decays can be roughly ordered according to the interaction energy.

Lambda into nucleon pion $m_X\approx 400\text{GeV}$ .

Sigma into nucleon pion $m_X\approx 400\text{GeV}$ .

5.2. Two-Body Non-Strange Decays of Mesons

$\Gamma =C{\left|{\psi }_{3,2}\right|}^2=\frac{G^2}{4\pi }{m}_i{x}^2\left(1-x^2\right)$ , $\Delta S=0$ , $l=\Delta I=3$ , $m=2$ , $x=\frac{m_f}{m_i}$ , $k=1$

${\pi }^{\pm }\to l\nu$ , $G=g_0$

$K^{\pm }\to l\nu$ , $G=g_1$

$K_S^0\to {\pi }^{+}{\pi }^{-}$ , $G=2g_1\alpha 443$ , $K_S^0\to {\pi }^0{\pi }^0$ , $G=2g_1\alpha 443/\sqrt{2}$

$K^{\pm }\to {\pi }^{\pm }{\pi }^0$ , $G=2g_1\alpha \sqrt{443}$

$K_L^0\to {\pi }^{+}{\pi }^{-}$ , $G=2g_1\alpha$ , $K_L^0\to {\pi }^0{\pi }^0$ , $G=2g_1\alpha /\sqrt{2}$

Table 6. Strange hyperon decays with pions.

The data for the non-strange two-body meson decays are shown in Table 7.

The decays can be roughly ordered according to the interaction energy

Pion-lepton $m_X\approx 100\text{GeV}$ ,

Kaon-lepton: $m_X\approx 400\text{GeV}$ ,

Kaon-pion: $m_X\approx 600\text{GeV}$ ,

Short-lived K_s0-pion: $m_X\approx 150\text{GeV}$ ,

Long-lived K_L0-pion: $m_X\approx 3200\text{GeV}$ .

5.3. Three-Four-Body Decays of Strange Mesons

$\Gamma =C{\left|{\psi }_{l,m}\right|}^2=\frac{G^2}{4\pi }{m}_i{\left(1-x^2\right)}^l$ , $\left|\Delta S\right|=1$ , $l=\Delta I=2$ , $m=2$ , $x=\frac{m_f}{m_i}$ , $k=1$

except $K^{\pm }\to {\pi }^{\pm }{\pi }^{+}{\pi }^{-}\gamma$ , where $\Delta I=1$ , $m=1$

$K^{\pm }\to {\pi }^{0}l\nu$ , $G=g_1\sqrt{\frac{\alpha }{2}}$

$K_L^0\to {\pi }^{\pm }l\nu$ , $G=g_1\sqrt{\alpha }$

$K^{\pm }\to {\pi }^{\pm }{\pi }^{+}{\pi }^{-}$ , $G=2.53g_1\sqrt{\alpha }$

$K^{\pm }\to {\pi }^{\pm }{\pi }^0{\pi }^0$ , $G=2.53g_1\sqrt{\frac{\alpha }{2}}$

$K_L^0\to {\pi }^0{\pi }^0{\pi }^0$ , $G=2g_1\sqrt{\alpha }$

$K_L^0\to {\pi }^{+}{\pi }^{-}{\pi }^0$ , $G=2g_1\sqrt{\alpha }/\sqrt{3/2}$

$K_L^0\to {\pi }^0{\pi }^{+}{e}^{-}{\nu }_e$ , $G=g_1\frac{\alpha }{\pi }$

$K^{\pm }\to {\pi }^{\pm }{\pi }^{\mp }{l}^{\pm }\nu$ , $K^{\pm }\to {\pi }^0{\pi }^0{l}^{\pm }\nu$ , $G=g_1\frac{\alpha }{\pi }$

$K^{\pm }\to {\pi }^0{\pi }^{\pm }\gamma$ , $G=g_1(\; \alpha \; 2\; )$

$K^{\pm }\to {\pi }^{\pm }{\pi }^{+}{\pi }^{-}\gamma$ , $G=g_1\alpha \sqrt{2}$

The data for the three-four-body decays of strange mesons are shown in Table 8.

The decays can be roughly ordered according to the interaction energy

Table 7. Two-body non-strange decays of mesons.

Table 8. Three-four-body decays of strange mesons.

K⁺, $K_L^0$ into pi 2lepton $m_X\approx 1.8\text{TeV}$

K⁺, $K_L^0$ into 3 pi $m_X\approx 150\text{GeV}$

K⁺, $K_L^0$ into 2 pi 2lepton $m_X\approx \mathrm{7...10}\text{TeV}$

K⁺ into 2pi photon $m_X\approx 5.7\text{TeV}$

K⁺ into 3 pion photon $m_X\approx 3.5\text{TeV}$

5.4. Three-Body Decays of Strange Hyperons

$\Gamma =C{\left|{\psi }_{l,m}\right|}^2=\frac{G^2}{4\pi }{m}_i^4{\left(1-x^2\right)}^l$ , $\left|\Delta S\right|=1$ , $l=\Delta I=2$ , $m=2$ , $x=\frac{m_f}{m_i}$ , $k=4$

with $g_{h2}=1.4\times {10}^{-8}{\text{GeV}}^{-3/2}$

$\Lambda \to pl\nu$ , $G=g_{h2}\sqrt{3}$

${\Sigma }^{-}\to nl\nu$ , $G=g_{h2}2$

The data for the three-body decays of strange hyperons are shown in Table 9.

The decays can be roughly ordered according to the interaction energy

Λ into pi 2lepton $m_X\approx 1.2\text{TeV}$

Σ into pi 2lepton $m_X\approx 1.7\text{TeV}$

5.5. Non-Strange Leptonic Three-Body Decays

$A\text{'}\to Ae\nu \left(\Delta S=0\right)$

$\Gamma =C{\left|{\psi }_{4,4}\right|}^2=G^2{m}_i^5{\left(1-x^2\right)}^4$ , $l=\Delta I=4$ , $m=4$ , $k=5$

${\pi }^{\pm }\to {\pi }^0{e}^{\pm }\nu$ , $G=G_0/\sqrt{192\times 50{\pi }^3}$

$n\to p{e}^{-}{\bar{\nu }}_e$ , $G=G_0/\sqrt{192\times 175{\pi }^3}$

${\Sigma }^{\pm }\to \Lambda e^{\pm }\nu$ , $G=G_0/\sqrt{192\times 65{\pi }^3}$

${\mu }^{-}\to e^{-}{\bar{\nu }}_e{\nu }_{\mu }$ , ${\tau }^{-}\to e^{-}{\bar{\nu }}_e{\nu }_{\tau }$ , ${\tau }^{-}\to {\mu }^{-}{\bar{\nu }}_{\mu }{\nu }_{\tau }$ , $G=G_0/\sqrt{192{\pi }^3}$

The data for non-strange leptonic three-body decays are shown in Table 10.

Here pure-leptonic transitions are bi-quark transitions

$n\to pe\bar{\nu }$ becomes $du\to uue\bar{\nu }$

${\Sigma }^{+}\to \Lambda \bar{e}\nu$ becomes $uu\to ud\bar{e}\nu$

The decays can be roughly ordered according to the interaction energy

lepton into lepton 2 neutrino $m_X\approx 700\text{GeV}$

pi into pi 2 lepton $m_X\approx 300\text{GeV}$

neutron decay n ->p e νe $m_X\approx 100\text{GeV}$

Σ into Λ 2lepton $m_X\approx 800\text{GeV}$

5.6. Three-Body Decays Eta-Pions

The decay width is [24]

$\Gamma =C{\left|{\psi }_{4,4}\right|}^2=\frac{G^2{m}_i}{4\pi }{\left(1-x^2\right)}^4$ , $l=\Delta I=4$ , $m=4$ , $k=1$

$\eta \to {\pi }^0{\pi }^0{\pi }^0$ , $\eta \to {\pi }^{+}{\pi }^{-}{\pi }^0$ , $G=0.0145$

$\eta \to {\pi }^{+}{\pi }^{-}\gamma$ , $G=0.00213$

The data for three-body eta-pion decays are shown in Table 11.

The decays can be roughly ordered according to the interaction energy

Table 9. Three-body decays of strange hyperons.

Table 10. Non-strange leptonic three-body decays.

Table 11. Three-body decays eta-pions.

eta into 3 pion $m_X\approx 0.3\text{GeV}$

eta into 2 pion photon $m_X\approx 1\text{GeV}$

5.7. Photon-Radiative Decays

The decay width is [24] [25] [26]

$\Gamma =C{\left|{\psi }_{3,3}\right|}^2=\frac{G^2{m}_i^3}{4\pi }{\left(1-x^2\right)}^3$ , $l=\Delta I=3$ , $m=3$ , $k=3$

with $\alpha =\frac{e^2}{4\pi }$ , $g_{ph}\text{'}=\text{0}\text{.138}$

pseudoscalar mesons $P\to \gamma \gamma$ , $P={\pi }^0,\eta ,{\eta }^{\prime }$ theory $\Gamma \left(P\to \gamma \gamma \right)=\frac{e^4{g}_{ph}^2}{64\pi }{m}_P^3$ ,

$x=0$ , $G=2\pi \alpha C_1{g}_{ph}\text{'}$ , $C_1=1,\sqrt{5/4},\sqrt{5/3}$

$\Gamma =C{\left|{\psi }_{2,2}\right|}^2=\frac{G^2{m}_i^5}{4\pi }{\left(1-x^2\right)}^2$ , $l=\Delta I=2$ , $m=2$

$g_{ph}=9.769\times {10}^{-9}$ , $G=C_1{g}_{ph}$

hyperons $\Lambda \to n\gamma$ , ${\Sigma }^{+}\to p\gamma$ , ${\Xi }^0\to \Lambda \gamma$ , ${\Xi }^0\to {\Sigma }^0\gamma$ , ${\Xi }^{-}\to {\Sigma }^{-}\gamma$ , $C_1=\sqrt{7/2},2,1,\sqrt{8},1/\sqrt{2}$

The data for photon-radiative decays are shown in Table 12.

The decays can be roughly ordered according to the interaction energy

pi, eta into 2 photon $m_X\approx 20\text{GeV}$

Λ, Σ into nucleon photon $m_X\approx 130\text{GeV}$

Xi into Λ photon $m_X\approx 180\text{GeV}$

Xi into Σ photon $m_X\approx 100,\mathrm{...},200\text{GeV}$

6. Characterization and Calculation of Different Types of Decays Based on Interaction Energy

6.1. Table of Decays Based on Interaction Energy

In the following Table 13, are shown the collected decay data from chap.5.

In the above table, the decays are grouped according to type and interaction energy m_X.

Consider the general decay

$P_{in}\to P_1+P_2+P_3+P_4$

In the table above, the column P_in contains the structure of the original particle, the column P_i contains the structures of the outgoing particles, separated by

Table 12. Photon-radiative decays.

slash, the rows m₁, ···, m₄ and m_X contain the respective mass.

The configuration is described either by quarks (like Λ = uds) or by l (lepton) or by Z, W.

The scheme in the last column describes the QHCD/QCD model of the interaction energy with number of active hc-bosons, e.g. sd’(2h) → Z → π⁰(2h) for the decay Ξ → Λ π.

E.g. the generic decay Λ/Σ → n π has the incoming configuration P_in = uds and the outgoing generic configuration P₁₂ = (n = udd)/(π⁰ = (uu’-dd’)), with the interaction energy m_X ≈ 400 GeV, and the decay scheme sd’(2h) → Z → π⁰, where the significant incoming current is $s\bar{d}$ interacting via 2 hc-bosons, the intermediate boson is the Z-boson, and the outgoing current is ${\pi }^0=\left(u\bar{u}-d\bar{d}\right)/\sqrt{2}$ . The number of active hc-bosons (or active gluons, in the pion-mediated decays) determines roughly the energy level.

Discussion of the results

The table reveals a simple principle for the scheme:

$q_1{\bar{q}}_2\to b\to p$ or ${\bar{q}}_1{q}_2\to b\to p$ , where q₁, q₂ are quarks in the incoming quark-current, b is the mediating boson $b=W,Z,{\pi }^0$ , p are the outgoing particles, $p={\pi }^0,\pi ,W,\gamma$ , where p can be represented as one or more quark-currents except for the photon γ, which is itself the electromagnetic current.

The resulting interaction energy m_X in the table above is not distributed uniformly, but accumulates around certain values, the energy classes.

$E_{h1}\approx 150\text{GeV}$ for 1 hc-boson

$E_{h2}\approx 400\text{GeV}$ for 2 hc-bosons

$E_{h4}\approx 700\text{GeV}$ for 4 hc-bosons

$E_{h6}\approx 1500\text{GeV}$ for 6 hc-bosons

$E_{h12}\approx 3500\text{GeV}$ for non-diagonal 12 hc-bosons outgoing W (1hcb)

$E_{h12,3h}\approx 5700\text{GeV}$ for non-diagonal 12 hc-bosons outgoing W (3hcb)

$E_{h15}\approx 7500\text{GeV}$ for all 15 hc-bosons outgoing W (3hcb)

$E_{h15,3h}\approx 9000\text{GeV}$ for all 15 hc-bosons outgoing W (6hcb)

$E_{c1}\approx 0.3\text{GeV}$ for 3 gluons (color interaction, factor 1000 weaker than hc-interaction)

Table 13. Decays based on interaction energy.

$E_{c6}\approx 7\text{GeV}$ for 6 non-diagonal gluons; $E_{c8}\approx 20\text{GeV}$ for all 8 gluons

For weak decays the energy span in m_X is roughly: $\frac{E_{h15}}{E_{h1}}=\frac{9000\text{GeV}}{150\text{GeV}}=60$ ,

so the energy span scales like $\frac{E_{h15}}{E_{h1}}=60\approx {\left(n_h\right)}^{3/2}$

6.2. The Interaction Energy and the Decay Width

In 2.1 a general relationship between the interaction energy m_X and the decay width Γ was derived:

$\frac{m_X}{m_i}=f_I{\left(\frac{m_i}{\Gamma }\right)}^{1/4}$ (21)

where $f_I=\frac{I_{\Gamma }^{1/4}}{2\sqrt{2}}$

The following plot in Figure 13 depicts this relationship for all 54 decays of the quarks u, d, s and all leptons, dealt with in this chapter [2] .

The x-axis is $x={\left(\frac{m_i}{\Gamma }\right)}^{1/4}$ , the y-axis is $y=\frac{m_X}{m_i}$ , the labels consist of the first

3 characters of the name of the corresponding decay, followed by the number in the total decay table, e.g. pi0 ->γ γ has the number 47, and the label “pi047”.

One sees immediately, that the decays separate in two large groups: those with x > 1000 are weak, i.e. hypercolor decays, those with x < 60 are strong (pure color) decays.

If there are 1 or 2 photons on the right side, then the electromagnetic Lagrangian component is used in the calculation in chap.7.

Figure 13. Interaction energy m_X in dependence of initial mass-energy m_i and decay width Γ.

In the pure-color decays only the color SU(3)-Lagrangian is used, in the weak decays both the SU(3) and the hypercolor SU(4)-Lagrangian is used.

7. Numerical Calculation: Method and Results

Schematics: calculated, observed interaction energy

Introduction of extended SU(4)-preon-model SU4PM

In this chapter, we follow a theoretical scheme, different from the phenomenological ansatz from chap. 3.

We calculate the interaction energy directly from the minimization of the action, based on the Lagrangian of the gauge-field theory of the underlying interaction, SU(1)-QED for electromagnetic interaction with photons, SU(3)-QCD for color interaction with 8 gluon-fields, SU(4)-QHCD for extended weak (hypercolor hc) interaction with 15 hc-boson-fields [5] [10] [27] - [32] .

The SU(4)-QHCD model of extended weak (hypercolor) interaction introduced in [2] , treats the Pauli SU(2)-weak interaction as a Yukawa-approximation via massive (W, Z)-bosons and extends it to SU(4)-hypercolor interaction with four charges, 15 hc-boson fields and two subparticles called preons.

With the weak interaction extended to SU(4)-QHCD, Standard Model (SM) becomes the extended SU(4)-preon-model (SU4PM).

The SU4PM model allows to calculate the masses of the SM remarkably well, reducing 29 parameters of the SM to 7 [2] [29] [33] .

In the following chap. 7.1 we present the basics of the SU4PM model, which the numerical calculation of decays is based on.

In SU4PM, the action $S={\displaystyle \int L\left(u_i\left(x^{\mu }\right),A_i\left(x^{\mu }\right)\right){\text{d}}^{4}x}$ depends on the total Lagrangian $L=L_{in}+L_{out}+L_{int}$ , where each Lagrangian contains the determining fields in the process hyper-color $L_{QHCD}$ , color $L_{QCD}$ , electromagnetic $L_{QED}$ , e.g. for the neutron decay $L=L_{QHCD}+L_{QED}$ .

The minimization of action $S={\displaystyle \int L\left(u_i\left(x^{\mu }\right),A_i\left(x^{\mu }\right)\right){\text{d}}^{4}x}=\min$ with condition $E_{in}=E_{out}$ , yields a solution in preons and fields $u_i,A_{g,j},A_{c,j},A_{e,j}$ with energies $E\left(u_i\right),E\left(A_{g,j}\right),E\left(A_{c,j}\right),E\left(A_{e,j}\right)$ , and interaction energy $m_{Xcal}$ , where

$m_{Xcal}={\displaystyle \underset{i}{\sum }{E}_{in}\left(u_i\right)}+{\displaystyle \underset{j}{\sum }{E}_{in}\left(A_j\right)}={\displaystyle \underset{i}{\sum }{E}_{out}\left(u_i\right)}+{\displaystyle \underset{j}{\sum }{E}_{out}\left(A_j\right)}$ .

The calculated total energy $m_{Xcal}$ is compared to the observed value $m_{Xexp}$ derived from the observed decay width ${\Gamma }_{obs}$ .

The agreement is quite good (see chap. 7.3).

7.1. The Configuration of the Standard Model in the Extended SU(4)-Preon-Model

Every basic particle of the SM is assigned a preon and a hc-boson configuration [2] [29] [32] .

The preon configuration of a fermion (leptons and quarks) occupies two of the 4 positions in a hc-quadruplet by a Dirac-bispinor, e.g. for electron with

index pair (1,3) we have $\left(\begin{array}{c}rL-\\ 0\end{array}\right)$ in position 1 and $\left(\begin{array}{c}rR-\\ 0\end{array}\right)$ in position 3,

according to the hc-charge. The hc-quadruplet has the hc-charges (L−, L+, R−, R+).

There are 3 possible hc-boson configurations for an index-pair (i,j), which are consistent with the SU(4)-symmetry: 1 hc-boson Aij corresponding to first generation of flavor = 1, 4 hc-bosons $Aij+\bar{A}ij+Akl+\bar{A}kl$ corresponding to flavor = 2 (the bar specifies the conjugate coupler, and (k,l) is the complementary index pair, e.g. for electron it is (2,4)), and finally all 15 hc-bosons corresponding to flavor = 3.

The fermions (leptons and quarks) have two independent preon-components u1 and u2, they form a bispinor with spin S = 1/2.

The bosons (weak boson W, Z, H) have only one independent preon-component u1, which is a linear combination of two preons, the spins add up to S = 1 for W and Z, or to S = 0 for H, e.g. for Z = Z0

$u1=\left(\left(rL-\right)+\left(rR-\right)\right)/\sqrt{2}$ and $Z0=\left(\left(\begin{array}{c}u1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ u1\end{array}\right),\left(\begin{array}{c}u1\\ 0\end{array}\right),\left(\begin{array}{c}0\\ u1\end{array}\right)\right)/\sqrt{2}$ . The weak

bosons W and Z0 are carrier of the residual weak interaction.

In the following, we present the basics of the SU(3)-color, the SU(4)-hypercolor, and its Yukawa weak Pauli force in three tables Tables 14(a)-(c) [29] .

Table 14. (a) SU(3) strong (color) interaction; (b) SU(4)-hypercolor interaction; (c) SU(2) weak Pauli interaction.

7.2. The Interaction Model and the Lagrangian in Two Examples

Example 1: neutron decay $n\to pe\bar{\nu }$

The basic idea of the Fermi model of weak 3-body decay in the Feynman picture mediated by the weak boson W is explained at the example of the neutron decay $n\to pe\bar{\nu }$ with the decay scheme $d\bar{u}\left(1h,3g\right)\to W\to W\left(1h\right)$ .

The incoming Lagrangian is $L\left(d\bar{u}\right)=L_{QHCD}\left(x^{\mu },\left\{u_1,u_2\right\},\left\{A{g}_4\right\}\right)+L_{QCD}\left(x^{\mu },\left\{u_1,u_2,0\right\},\left\{A{c}_1,A{c}_2,A{c}_3\right\}\right)$ with the quark wavefunctions $u_1=d=r^{-}{q}^{+}$ , $u_2=\bar{u}=r^{-}{q}^{-}$ in the hypercolor-SU(4)-preon model, and one hc-boson $A{g}_4$ corresponding to the SU(4) generalized Gell-Mann matrix ${\lambda }_4$ and the SU(4) index pair {1,3} and the interaction $r_L{}^{-}\leftrightarrow r_R{}^{-}$ in the hc-charge-quadruple $\left(r_L{}^{-},r_L{}^{+},r_R{}^{-},r_R{}^{+}\right)$ [2] . Furthermore, there are 3 gluons $\left\{A{c}_1,A{c}_2,A{c}_3\right\}$ , which carry the color interaction.

We recall that both L_QHCD and L_QCD have the generic form.

Dirac part $L_D=\bar{u}\left(i\hslash D_{\mu }{\gamma }^{\mu }-mc\right)u$ , covariant derivative $D_{\mu }={\partial }_{\mu }-ig{A}^a{}_{\mu }{\lambda }_a$ ,

with field $A^a{}_{\mu }$ , field part $L_{gf}=-\frac{1}{4}{F}^{a\mu \nu }F{}_{a\mu \nu }$ , field tensor

$F^a{}_{\mu \nu }={\partial }_{\mu }{A}^a{}_{\nu }-{\partial }_{\nu }{A}^a{}_{\mu }+g{f}^{abc}{A}^b{}_{\mu }{A}^c{}_{\nu }$ , where ${\lambda }_a$ are the Gell-Mann matrices, with the structure constants $f^{abc}$ of the respective Lie algebra (SU(3) or SU(4)) and ${\lambda }_a$ are the generators of the algebra,

From the preon composition of $d\bar{u}$ results the following form of the SU(4) quadruple wavefunction

$u_{11}=\left(r_L{}^{-}+q_L{}^{+}\right)/\sqrt{2}$ , $u_{12}=\left(r_R{}^{-}+q_R{}^{+}\right)/\sqrt{2}$ , $d=\left(\left(\begin{array}{c}{u}_{11}\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}{u}_{12}\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right)\right)$

$u_{21}=\left(r_L{}^{-}+q_L{}^{-}\right)/\sqrt{2}$ , $u_{22}=\left(r_R{}^{-}+q_R{}^{-}\right)/\sqrt{2}$ , $\bar{u}=\left(\left(\begin{array}{c}{u}_{21}\\ u_{21}\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}{u}_{21}\\ u_{21}\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right)\right)/\sqrt{2}$

The outgoing Lagrangian is $L\left(W\right)=L_{QHCD}\left(x^{\mu },\left\{u_3,u_3\right\},\left\{Ag{\text{'}}_4\right\}\right)$ with the weak boson W $u_3=r_L{}^{-}{r}_R{}^{-}$ and another hc-boson $Ag{\text{'}}_4$ .

$u_{31}=r_L{}^{-}$ , $u_{32}=r_R{}^{-}$ , $W=\left(\left(\begin{array}{c}{u}_{31}\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}{u}_{31}\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right)\right)$

The interaction Lagrangian is the Fermi current-current interaction with the mediating exchange boson

$L_{JJ}\left(J\left(d\bar{u}\right),J\left(W\right)\right)=\frac{\left(u_1{}^{+}{\gamma }^{\mu }{u}_2\right)\left(u_3{}^{+}{\gamma }_{\mu }{u}_4\right)}{m_X^2}$ , with the notation Dirac-conjugate

$u_1{}^{+}$

The interaction energy is

$\begin{array}{c}{m}_X=E_{out}=E\left(u_3\right)+m_W+E\left(Ag{\text{'}}_4\right)\\ =E_{in}=E\left(u_1\right)+E\left(u_2\right)+m_u+m_d+E\left(A{g}_4\right)+{\displaystyle \underset{i=1}{\overset{3}{\sum }}A{c}_i}\end{array}$

So we have in total two particle configurations, the incoming $n\bar{p}$ and the outgoing $e\bar{\nu }$ , each with an interaction Lagrangian, coupled by the Fermi current-current interaction, and mediated by the corresponding W-boson $W=r_L{}^{-}{r}_R{}^{-}$ .

In the incoming system $d\bar{u}$ we have to take into account the color interaction of the quarks $L_C\left(d\bar{u}\right)=L_{QCD}\left(x^{\mu },\left\{u_1,u_2\right\},\left\{A{c}_2,A{c}_5,A{c}_7\right\}\right)$ in the basic gluon configuration with 3 rgb-gluons.

Feynman diagram of the decay $n\to pe\bar{\nu }$ , with the notation of the antiparticle $\bar{p}=p^c$ (conjugate), is shown in Figure 14.

The quark-hc-boson-gluon decay-scheme in the SU4PM model $d\bar{u}\left(1h,3g\right)\to W\to W\left(1h\right)$ , where the mediating boson $W=r_L{}^{-}{r}_R{}^{-}$ acts via the current-current-interaction L_JJ is shown in Figure 15.

In the decay-scheme the weak (SU(4)) interaction is carried on the left side by 1 h = 1 hypercolor SU(4) boson Ag₄, and the color (SU(3)) interaction by

3 g = 3 (anticoupler) gluons Ac₂ Ac₅ Ac₇.

Figure 14. Feynman diagram of the decay $n\to pe\bar{\nu }$ .

Figure 15. Quark decay-scheme $d\bar{u}\left(1h,3g\right)\to W\to W\left(1h\right)$ of the decay $n\to pe\bar{\nu }$ .

The incoming color Lagrangian is

$L_{QCD}\left(x^{\mu },\left\{u_1,u_2,0\right\},\left\{A{c}_1,A{c}_2,A{c}_3\right\}\right)$ , where the color triple is $\left\{u_1,u_2,0\right\}$ , on which act the 3x3 color Gell-Mann matrices ${\lambda }_i$ .

On the right side, the weak (SU(4)) interaction is carried by 1 h = 1 hypercolor SU(4) boson Ag₄ and there is no color interaction, as the mediating boson W has only a weak charge, no color charge.

Example 2: 4-body kaon-pion photonic decay $K^{+}\to {\pi }^{+}{\pi }^{+}{\pi }^{-}\gamma$

We illustrate the calculation ansatz in more detail in the more complicated and computationally much more challenging example of the 4-body kaon-pion photonic decay $K^{+}\to {\pi }^{+}{\pi }^{+}{\pi }^{-}\gamma$ with the quark-hcboson-gluon decay scheme $u\bar{s}\left(12h,3g\right)\to W\to {\pi }^{+}{\pi }^{+}{\pi }^{-}\left(6h,3g,1\gamma \right)$ .

The Feynman diagram of the process is shown in Figure 16.

The corresponding decay-scheme in the SU4PM model is shown in Figure 17.

The incoming Lagrangian is

$L\left(u\bar{s}\right)=L_{QHCD}\left(x^{\mu },\left\{u_1,u_2\right\},\left\{A{g}_n\right\}\right)+L_{QCD}\left(x^{\mu },\left\{u_1,u_2,0\right\},\left\{A{c}_2,A{c}_5,A{c}_7\right\}\right)$ , with $K^{+}=u\bar{s}$ , with the quark wavefunctions $u=r^{+}{q}^{+}$ , $\bar{s}=r^{+}{q}^{-}$ ,

$u_{11}=\left(r_L{}^{+}+q_L{}^{+}\right)/\sqrt{2}$ , $u_{12}=\left(r_R{}^{+}+q_R{}^{+}\right)/\sqrt{2}$ , $u=\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}{u}_{11}\\ u_{11}\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}{u}_{12}\\ u_{12}\end{array}\right)\right)/\sqrt{2}$

$u_{21}=\left(r_L{}^{+}+q_L{}^{-}\right)/\sqrt{2}$ , $u_{22}=\left(r_R{}^{+}+q_R{}^{-}\right)/\sqrt{2}$ , $\bar{s}=\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}0\\ u_{21}\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}{u}_{21}\\ u_{21}\end{array}\right)\right)$

and 12 non-diagonal hc-bosons $A{g}_n$ corresponding to the non-diagonal SU(4) generator matrices ${\lambda }_i$ and the SU(4) indices $n=\left\{1,2,4,5,6,7,9,10,11,12,13,14\right\}$ .

It contains also 3 gluons $\left\{A{c}_2,A{c}_5,A{c}_7\right\}$ which carry the color interaction.

The outgoing Lagrangian is

$\begin{array}{c}L\left({\pi }^{+}{\pi }^{-}{\pi }^{+}\right)=L_{QHCD}\left(x^{\mu },\left\{u_3,u_4,u_5\right\},\left\{Ag{\text{'}}_i\right\}\right)\\ +L_{QCD}\left(x^{\mu },\left\{u_3,u_4,u_5\right\},\left\{Ac{\text{'}}_2,Ac{\text{'}}_5,Ac{\text{'}}_7\right\}\right)+L_e\left({\pi }^{+}{\pi }^{-}{\pi }^{+}\right)\end{array}$ , indices

$i=\left\{1,4,6,9,11,13\right\}$ , with the pions and their corresponding wavefunctions

${\pi }^{+}{\pi }^{-}=u\bar{d}d\bar{u}=r_L{}^{-}+r_R{}^{+}+q_L{}^{-}+q_R{}^{+}$

$u_{31}=u_{41}=\left(r_L{}^{-}+q_L{}^{-}\right)/\sqrt{2}$ , $u_{32}=u_{42}=\left(r_R{}^{+}+q_R{}^{+}\right)/\sqrt{2}$ ,

${\pi }^{+}{\pi }^{-}=\left(\left(\begin{array}{c}{u}_{31}-u_{41}\\ u_{31}-u_{41}\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{c}{u}_{32}-u_{42}\\ u_{32}-u_{42}\end{array}\right)\right)/2$

Figure 16. Feynman diagram of the decay $K^{+}\to {\pi }^{+}{\pi }^{+}{\pi }^{-}\gamma$ .

Figure 17. Quark decay-scheme $u\bar{s}\left(12h,3g\right)\to W\to {\pi }^{+}{\pi }^{+}{\pi }^{-}\left(6h,3g,1\gamma \right)$ of the decay $K^{+}\to {\pi }^{+}{\pi }^{+}{\pi }^{-}\gamma$ .

${\pi }^{+}=u\bar{d}=r_L{}^{+}+r_R{}^{+}+q_L{}^{-}+q_R{}^{+}$ , $u_{51}=\left(r_L{}^{+}+q_L{}^{-}\right)/\sqrt{2}$ , $u_{52}=\left(r_R{}^{+}+q_R{}^{-}\right)/\sqrt{2}$ ,

${\pi }^{+}=\left(\left(\begin{array}{c}0\\ u_{51}\end{array}\right),\left(\begin{array}{c}0\\ u_{51}\end{array}\right),\left(\begin{array}{c}0\\ u_{52}\end{array}\right),\left(\begin{array}{c}0\\ u_{52}\end{array}\right)\right)/\sqrt{2}$

and the 6 hc-bosons $Ag{\text{'}}_i$ , which are the 6 couplers of SU(4).

It contains also 3 diagonal gluons $\left\{Ac{\text{'}}_2,Ac{\text{'}}_5,Ac{\text{'}}_7\right\}$ which carry the color interaction.

The interaction Lagrangian is

$L_{JJ}\left(J\left(u\bar{s}\right),J\left({\pi }^{+}{\pi }^{-}{\pi }^{+}\right)\right)=\frac{\left(u_1{}^{+}{\gamma }^{\mu }{u}_2\right)\left(u_3{}^{+}{\gamma }_{\mu }{u}_3+u_4{}^{+}{\gamma }_{\mu }{u}_4+u_5{}^{+}{\gamma }_{\mu }{u}_5\right)}{m_X^2}$ , with the

notation Dirac-conjugate $u_1{}^{+}$ .

The interaction energy is

$\begin{array}{c}{m}_X=E_{out}=E\left(u_3\right)+E\left(u_4\right)+E\left(u_5\right)+3m_{\pi }+{\displaystyle \underset{i}{\sum }E\left(Ag{\text{'}}_i\right)}+{\displaystyle \underset{i}{\sum }E\left(Ac{\text{'}}_i\right)}+A{e}_0\\ =E_{in}=E\left(u_1\right)+E\left(u_2\right)+m_u+m_s++{\displaystyle \underset{n}{\sum }E\left(A{g}_n\right)}+{\displaystyle \underset{i}{\sum }E\left(A{c}_i\right)}\end{array}$

So we have in total two particle configurations, the incoming $K^{+}=u\bar{s}$ and the outgoing ${\pi }^{+}{\pi }^{-}{\pi }^{+}$ , each with an interaction Lagrangian, coupled by the Fermi current-current interaction, and mediated by the corresponding W-boson $W=r_L{}^{-}{r}_R{}^{-}$ ,

In the incoming system $K^{+}=u\bar{s}$ and the outgoing ${\pi }^{+}{\pi }^{-}{\pi }^{+}$ we have to take into account the color interaction of the quarks $L_C\left(u\bar{s}\right)=L_{QCD}\left(x^{\mu },\left\{u_1,u_2,0\right\},\left\{A{c}_2,A{c}_5,A{c}_7\right\}\right)$ and $L_C\left({\pi }^{+}{\pi }^{-}{\pi }^{+}\right)=L_{QCD}\left(x^{\mu },\left\{u_3,u_4,u_5\right\},\left\{Ac{\text{'}}_2,Ac{\text{'}}_5,Ac{\text{'}}_7\right\}\right)$ in the basic gluon configuration with 3 rgb-gluons.

The outgoing photon is active in the additional third electromagnetic Lagrangian $L_e\left({\pi }^{+}{\pi }^{-}{\pi }^{+}\right)=L_e\left(x^{\mu },\left\{u_3,u_4,u_5\right\},\left\{A{e}_0\right\}\right)$ .

7.3. The Calculation Method

Now we minimize the action $S={\displaystyle \int L\left(x^{\mu },u_i,A{g}_i\right)}{r}^2\sin \theta \text{d}t\text{d}r\text{d}\theta \text{d}\phi$ for the total Lagrangian $L\left(x^{\mu },u_i,A{g}_i\right)=L\left(d\bar{u}\right)+L_{JJ}\left(W\right)+L\left(J\left(d\bar{u}\right),J\left(W\right)\right)+L_C\left(d\bar{u}\right)$ under the constraint of energy conservation $E\left(d\bar{u}\right)=E\left(W\right)$ , as required in the Feynman diagram of the process.

We have for the particle wavefunctions $\left\{u_1,u_2,u_3\right\}$ the normalization condition ${\displaystyle \int {\left|u_i\right|}^2{\text{d}}^{3}x=1}$ and for the field bosons we set up a boundary condition for r = r₀ $A{g}_i\left(r_0\right)=0$ and $A{c}_i\left(r_0\right)=0$ and the Lorenz-gauge-condition ${\partial }_{\mu }{\left(A{g}_i\right)}^{\mu }=0$ and ${\partial }_{\mu }{\left(A{c}_i\right)}^{\mu }=0$ .

The energy, length, and time are made dimensionless by using the units:

E( $E_0=\frac{\hslash c}{1\text{am}}=0.196\text{TeV}$ ), r(fm), t(am/c) am = 10⁻¹⁸ m. We can assume axial

symmetry, so we can set φ = 0 and use the spherical coordinates $\left(t,r,\theta \right)$ .

We choose the equidistant lattice for the intervals $\left(t,r,\theta \right)\in \left[0,1\right]\times \left[0,1\right]\times \left[0,\pi \right]$ with 21 × 21 × 11 points and, for the minimization n_sub in parallel, n_sub random sublattices of length l_sub, where n_sub = 8 or 16, and l_sub = 25 or 50 or 100 according to the complexity of the corresponding Lagrangian.

$l\left[ix,j\right]=\left\{\left\{\left(t_{i1},r_{i2},t_{i3}\right)|\left(i1,i2,i3\right)=random\left(lattice,j=1,\cdots ,l_{sub}\right)\right\}|ix=1,\cdots ,n_{sub}\right\}$ .

For the Ritz-Galerkin expansion we use the 12 functions $f_k\left(r,\theta \right)=\left\{bfunc\left(r,r_0,d{r}_0\right)r^{k_1},k_1=0,\cdots ,n_r\right\}\times \left\{\left({\cos }^{k_2}\theta ,{\cos }^{k_2}\theta \sin \theta \right),k_2=0,\cdots ,n_{\theta }\right\}$

The action $S={\displaystyle \int L\left(x^{\mu },u_i,A{g}_i\right)}{r}^2\sin \theta \text{d}t\text{d}r\text{d}\theta \text{d}\phi$ becomes a mean-value on the sublattice $l\left[ix\right]$

$\tilde{S}\left[ix\right]=\frac{1}{N\left(l\left[ix\right]\right)}{\displaystyle \underset{x\in l{\left[ix\right]}_{sub}}{\sum }L\left(x,u_i,A{g}_i\right)}2\pi V_{tr\theta }$ , where $V_{tr\theta }=\pi$ the

$\left(t,r,\theta \right)$ -volume and $l_{sub}=N\left(l\left[ix\right]\right)$ is the number of points. We impose the boundary condition for $A{g}_i\left(r=r_0\right)=0$ via penalty-function (imposing exact conditions is possible, but slows down the minimization process enormously).

$\tilde{S}$ is minimized n_sub x in parallel with the Mathematica-minimization method “simulated annealing”.

The proper parameters of the particles $u_i$ and the hc-bosons $A{g}_i$ are:

$par\left(p_i\right)=\left\{E{u}_i,a_i,r{u}_i,\theta u_i,dr{u}_i\right\}$ , $par\left(A{g}_i\right)=\left\{E{A}_i,a{A}_i\right\}$ , $par\left(A{c}_i\right)=\left\{EA{c}_i,aA{c}_i\right\}$

The complexities and execution times (on a 2.7 GHz Xeon E5 work-station) differ greatly for different decays.

For the neutron decay $n\to pe\bar{\nu }$ with the scheme $d\bar{u}\left(1h\right)\to W\to W\left(1h\right)$ (1hc-boson on both sides) and color interaction $L\left(d\bar{u},3g\right)$ with basic 3 gluons complexity (Lagrangian) = (3.7 + 4.8) × 10⁶ terms, minimization time t (minimization) = 111 s.

The mathematical details of the calculation, and the results can be studied in depth in the corresponding Mathematica programs [34] .

7.4. Discussion of Calculated Decays

Table 15 of decays with calculation results mX and experimental values mXexp according to the formula in 2.1 from the observed decay width Γobs, is as follows [34] .

Table description

The scheme (last) column describes the model of the decay, on which the calculation is based, where the notation q’ is used for the antiparticle $\bar{q}$ .

Here the calculation result (m_Xcal) and the value from decay time (m_Xexp) are given in GeV.

m_X(er) is the calculated m_X-value with uncertainty er in GeV.

E_col specifies the calculated color interaction energy in GeV and the number of active gluons on left side of the process, e.g. 250 (3 g), E_em is the electromagnetic energy of the involved photons, if any.

12 > and 12 > are the mean radius in am-units (1 am = 10 ⁻¹⁸ m) and its quantum “smear-out” in the left-side (incoming) part of the scheme.<> <>

The mean boson amplitude (hypercolor, color, electromagnetic) of the incoming and outgoing system Agi Aci Aei expressed in units am⁻¹ is given in column four.

$m_X=E\left(B_{med}\right)$ , where for weak decays the mediating boson is $B_{med}=W$ or $B_{med}=Z$ .

Classification according to m_X: strong decays

There are here 3 strong (color) decays: pion and eta decays, with scales $m_X\approx \left(0.3,7.5,20\right)\text{GeV}$ , mediated by a pion

η -> π0 π0 π0, η -> π0 π0 γ, π0/η -> γ γ

Strong decays have an assessed upper limit of interaction energy m_X for strong decays: $E_{c,max}=N_{comp}{M}_{max}$ ,where $M_{max}$ is the maximum energy-mass, for 1+2-generation $M_{max}=m_c=1.3\text{GeV}$ for charm-quark, and maximum number of components $N_{comp}=3+15$ , where 3 stands for 3 quarks, and 15 stands for 15 hc-bosons, so $E_{c,max}=18\times 1.3=23.4\text{GeV}$ .

Classification according to m_X: weak decays

The minimum interaction energy m_X for weak decays is $E_{w,min}=m_W=80.4\text{GeV}$ .

The weak decays considered here can be put into 3 categories.

- low interaction energy 100 - 400 GeV

$n\to pe\bar{\nu }$ , $m_X~200\text{GeV}$

schematic photonic $\Lambda /\Sigma /\Xi \to \gamma \mathrm{...}$ , $m_X=\mathrm{130...260}\text{GeV}$

schematic pionic $\Lambda /\Sigma /\Xi \to \pi \mathrm{...}$ , $m_X~400\text{GeV}$

schematic one-pion $K\to \pi$ , $m_X~160\text{GeV}$

schematic leptonic $K/\pi \to l\nu$ , $m_X=\mathrm{130...180}\text{GeV}$

-middle interaction energy 700 - 1700 GeV

schematic nucleonic $\Lambda /\Sigma \to \left(p/n\right)\nu$ , $m_X=\mathrm{1300...1700}\text{GeV}$

Table 15. Decays with calculation results mX and experimental values mXexp.

schematic pure leptonic $\mu /\tau \to l2\nu$ , $m_X~700\text{GeV}$

schematic leptonic $\Sigma \to \Lambda l\nu$ , $m_X~700\text{GeV}$

- high interaction energy kaon 3400 - 9200 GeV

schematic pionic-leptonic $K\to \pi l\nu$ , $m_X~2000\text{GeV}$

schematic pionic $K_L^0\to \pi \pi$ , $m_X~3400\text{GeV}$

schematic pionic-leptonic $K\to \pi \pi l\nu$ , $m_X=\mathrm{7600...9200}\text{GeV}$

schematic pionic-photonic $K\to 3\pi \gamma$ , $m_X~3600\text{GeV}$

schematic pionic-photonic $K\to 2\pi \gamma$ , $m_X~5700\text{GeV}$

Characterization of radius

The calculated radius r of decaying particle is a parameter of the ingoing Lagrangian, and is measured in am = 10⁻¹⁸ m.

For weak decays we obtain values $r=\mathrm{0.25...1.3}\text{am}$ and quantum smear-out $\Delta r~r$ .

For strong decays we obtain $r~0.3\text{am}$ .

The following plot Figure 18 presents the measured and calculated interaction energy described in the above table [2] [34] .

The decays above 80 GeV (=m_W) are weak (hypercolor) decays, those below 25 GeV (=6m_b, m_b = 4.2 GeV) are strong (color) decays, the observed m_X is dark-blue, the calculated m_X is red (with calculation error bar), the color energy for weak decays, respectively electromagnetic energy for strong decays is cyan.

Another interesting decay parameter is the mean radius 12> of the incoming system on the left side of the scheme, e.g. for the neutron decay<>

Figure 18. Measured and calculated interaction energy.

Figure 19. Mean radius in dependence of interaction energy.

Figure 20. Mean field boson amplitude in dependence of interaction energy.

n->p e νe, the incoming system is $n\bar{p}$ , in the decay scheme it is represented by $d\bar{u}$ [2] [34] . The plot of radius is shown in Figure 19.

It is interesting to see, that the mean radius separates basically into two groups: high-energy non-leptonic kaon-pion decays with 12 >>0.9 am and the remaining decays with 12 > <0.5 am, apart from the photonic Λ/Σ -> n γ.<> <>

The other important decay parameter is the mean (hypercolor, color, electromagnetic) field boson amplitude Agi for the weak decays, Aci for the color decays, of the incoming system, expressed in units am⁻¹ [2] [34] . The mean field boson amplitude is shown in Figure 20.

Again, the amplitude separates into two groups, amplitude ≥ 0.6 for the kaon-pion decays an pure leptonic decays, and the remaining with amplitude ≤ 0.3, with the outlier K+ -> π+ π0.

8. Conclusions

We introduce a two-step calculation method for calculation of general decay rates in the Standard Model, and apply it, producing results for a wide variety of decay processes, which are in good agreement with measurements.

The first step is an extended schematic formula by Chang [1] , based on extended isospin. It supports the generalized model of a decay-mediating virtual particle with interaction energy m_X, in analogy to the weak interaction mediated

by the W-boson with $G=\frac{G_F}{\sqrt{2}}=\frac{g^2}{8M_W^2}$ , where $m_X=M_W$ , g is the dimensionless

weak interaction constant, and $G_F=1.1663787\left(6\right)\times {10}^{-5}{\text{GeV}}^{-2}$ is the Fermi weak coupling constant.

The second step is a numerical Lagrangian calculation method, which calculates the interaction energy m_X of the process numerically by minimization of action from the Lagrangian.

First we derive in chap.2 formulas in the conventional way for selected examples: neutron, muon, pions and kaons.

In chap.2.8 and chap.2.9 we present the fundamental Fermi golden rule for 3-body and 2-body decays:

$\text{d}{\Gamma }_{3b}=\frac{{\left|M\left(k,p_1,p_2,p_3\right)\right|}^2}{2m}\frac{{\text{d}}^3{p}_1}{{\left(2\pi \right)}^{3}2E_1}\frac{{\text{d}}^3{p}_2}{{\left(2\pi \right)}^{3}2E_2}\frac{{\text{d}}^3{p}_3}{{\left(2\pi \right)}^{3}2E_3}{\left(2\pi \right)}^4{\delta }^4\left(k-p_1-p_2-p_3\right)$

$\text{d}{\Gamma }_{2b}=m\frac{{\left|M\left(k,p_1,p_2\right)\right|}^2}{2}\frac{{\text{d}}^3{p}_1}{{\left(2\pi \right)}^{3}2E_1}\frac{{\text{d}}^3{p}_2}{{\left(2\pi \right)}^{3}2E_2}{\left(2\pi \right)}^4{\delta }^4\left(k-p_1-p_2\right)$

and derive kinematic factors for these processes:

$I_{\Gamma 3s}\left(m,m_1,m_2,m_3\right)$ and $I_{\Gamma 2s}\left(m,m_1,m_2\right)$ .

In chap.3.1 we formulate the phenomenological formula:

$\Gamma ={\tilde{G}}^2{m}_i^k{\left|P_l{}^m\left(x\right)\right|}^2=\frac{G^2}{C_1}{m}_i^k{\left|P_l{}^m\left(x\right)\right|}^2$ , where $P_l{}^m\left(x\right)$ Legendre polynomial $m=l$ or $m=l+1$ , l = isospin I, $x=\frac{m_f}{m_i}$ mass ratio, $\tilde{G}=\frac{G}{\sqrt{C_1}}$ with G =

interaction constant, $m_i$ is the initial mass, k is the mass-power-coefficient.

The constant $C_1$ is process-dependent, standard value is $C_1=4\pi$ .

The phenomenological scheme classifies decays into seven classes, according to the values of k, l, and m.

The interaction constant G is independent of masses $m_i,m_f$ , and is in the same range within a class.

The seven classes discussed here are:

Strange hyperon-pion decays,

Two-body non-strange meson decays,

Three-four-body strange meson decays,

Three-body strange hyperon decays,

Non-strange leptonic three-body decays,

Three-body eta-pion decays,

Photon-radiative decays.

Also, we define and derive a formula for interaction energy m_X between the initial and final configuration of the decay process, which is the energy of the mediating boson in a weak decay.

In analogy to the weak interaction mediated by the W-boson $G=\frac{G_F}{\sqrt{2}}=\frac{g^2}{8M_W^2}$ ,

we make the ansatz for the matrix element M and the interaction energy m_X of the mediating boson:

$M=\frac{m_i^2}{8m_X^2}$ , so we obtain the decay width formula $\Gamma ={\left|M\right|}^2{I}_{\Gamma }m={\left(\frac{m^2}{8m_X^2}\right)}^2{I}_{\Gamma }m$

The process can be weak (W-Z-mediated Pauli interaction, $G~G_F$ ), electromagnetic (interaction constant $G~\alpha =1/137$ ) or strong $G~g_s$

The rest of chap. 3 deals with different special cases of the formula: muon, pions, kaon-pions, neutron, eta-pion, meson-2-photon decay, hyperon-photon.

In chap. 5 we show the actual form and results of the phenomenological formula for seven classes of decay processes, classified by the phenomenological scheme.

In chap. 6 we present the all calculation results from the phenomenological formula in tabular form and in graphic form of a plot.

In chap. 7.1 we describe the theoretical background of the numerical Lagrangian calculation method.

action $S={\displaystyle \int L\left(u_i\left(x^{\mu }\right),A_i\left(x^{\mu }\right)\right){\text{d}}^{4}x}=\min$ , condition E_in = E_out

$L=L_{in}+L_{out}+L_{int}$ Lagrangian

for SU(3)-QCD and hypercolor-SU(4)-weak-QFT(=QHCD)

Dirac part $L_D=\bar{u}\left(i\hslash D_{\mu }{\gamma }^{\mu }-mc\right)u$ , $D_{\mu }={\partial }_{\mu }-ig{A}^a{}_{\mu }{\lambda }_a$ , with hc-field $A^a{}_{\mu }$ , Lie structure constants $f^{abc}$

Field part $L_f=-\frac{1}{4}{F}^{a\mu \nu }F{}_{a\mu \nu }$ , field tensor $F^a{}_{\mu \nu }={\partial }_{\mu }{A}^a{}_{\nu }-{\partial }_{\nu }{A}^a{}_{\mu }+g{f}^{abc}{A}^b{}_{\mu }{\tilde{A}}^c{}_{\nu }$

For SU(3)-QCD $\Psi =\left(u_1,u_2,u_3\right)$ , e.g. proton $p=\left(u,u,d\right)$

For hypercolor-SU(4)-weak-QHCD $\Psi =\left(u_{L-},u_{L+},u_{R-},u_{R+}\right)$ , e.g. electron $e^{-}=\left(r_{L-},0,r_{R-},0\right)$

Generations $f_1\simeq 1A_g$ , $f_2\simeq 4A_g$ , $f_3\simeq 15A_g$

For QED $D_{\mu }={\partial }_{\mu }-ig{A}_{\mu }$ , $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$

$L_{QHCD}=L_{hc,D}\left(u_i,A_{g,j}\right)+L_{hc,f}\left(A_{g,j}\right)$ , ${\lambda }_a=15$ 4 × 4 Gell-Mann matrices

$L_{QCD}=L_{c,D}\left(u_i,A_{c,j}\right)+L_{c,f}\left(A_{c,j}\right)$ , ${\lambda }_a=8$ 3 × 3 Gell-Mann matrices

$L_{QED}=L_{e,D}\left(u_i,A_e\right)+L_{e,f}(\; A\; e\; )$

$L_{JJ}\left(J\left(d\bar{u}\right),J\left(W\right)\right)=\frac{\left(u_1{}^{+}{\gamma }^{\mu }{u}_2\right)\left(u_3{}^{+}{\gamma }_{\mu }{u}_4\right)}{m_X^2}$

S = min yields solution $u_i,A_{g,j},A_{c,j},A_{e,j}$ with energy $E\left(u_i\right),E\left(A_{g,j}\right),E\left(A_{c,j}\right),E\left(A_{e,j}\right)$ , total energy $m_{Xcal}=E_{in}=E_{out}$

In chap. 7.2 we give the details of the numerical action minimization procedure.

In chap. 7.3 we present the calculated parameters of the decay process

- the calculated and the experimental values of the interaction energy m_X in tabular form and in a graphical plot.

- in the ingoing particle values of color and electromagnetic energy E_col, E_em.

- field boson amplitudes weak-hcolor, strong-color. electromagnetic $\left(A_{g,i},A_{c,i},A_{e,i}\right)$ .

- radius r and its smear-out Δr.

The scheme of the decay process is formulated as follows:

$q_1{\bar{q}}_2\to b\to p$ or ${\bar{q}}_1{q}_2\to b\to p$ , where q₁, q₂ are quarks in the incoming quark-current, b is the mediating boson $b=W,Z,{\pi }^0$ , p are the outgoing particles, $p={\pi }^0,\pi ,W,\gamma$ , where p can be represented as one or more quark-currents except for the photon γ, which is itself the electromagnetic current.

The resulting interaction energy m_X in the table above is not distributed uniformly, but accumulates around certain values, the energy classes.

$E_{h1}\approx 150\text{GeV}$ for 1 hc-boson

$E_{h2}\approx 400\text{GeV}$ for 2 hc-bosons

$E_{h4}\approx 700\text{GeV}$ for 4 hc-bosons

$E_{h6}\approx 1500\text{GeV}$ for 6 hc-bosons

$E_{h12}\approx 3500\text{GeV}$ for non-diagonal 12 hc-bosons outgoing W (1 hcb)

$E_{h12,3h}\approx 5700\text{GeV}$ for non-diagonal 12 hc-bosons outgoing W (3 hcb)

$E_{h15}\approx 7500\text{GeV}$ for all 15 hc-bosons outgoing W (3 hcb)

$E_{h15,3h}\approx 9000\text{GeV}$ for all 15 hc-bosons outgoing W (6 hcb)

$E_{c1}\approx 0.3\text{GeV}$ for 3 gluons (color interaction, factor 1000 weaker than hc-interaction)

$E_{c6}\approx 7\text{GeV}$ for 6 non-diagonal gluons; $E_{c8}\approx 20\text{GeV}$ for all 8 gluons

For weak decays the energy span in m_X is roughly: $\frac{E_{h15}}{E_{h1}}=\frac{9000\text{GeV}}{150\text{GeV}}=60$ ,

So the energy span scales like $\frac{E_{h15}}{E_{h1}}=60\approx {\left(n_h\right)}^{3/2}$

The classification according to interaction energy m_X

For weak decays is as follows.

- Low interaction energy 100 - 400 GeV

$n\to pe\bar{\nu }$ , $m_X~200\text{GeV}$

Schematic photonic $\Lambda /\Sigma /\Xi \to \gamma \mathrm{...}$ , $m_X=\mathrm{130...260}\text{GeV}$

Schematic pionic $\Lambda /\Sigma /\Xi \to \pi \mathrm{...}$ , $m_X~400\text{GeV}$

Schematic one-pion $K\to \pi$ , $m_X~160\text{GeV}$

Schematic leptonic $K/\pi \to l\nu$ , $m_X=\mathrm{130...180}\text{GeV}$

- Middle interaction energy 700 - 1700 GeV

Schematic nucleonic $\Lambda /\Sigma \to \left(p/n\right)\nu$ , $m_X=\mathrm{1300...1700}\text{GeV}$

Schematic pure leptonic $\mu /\tau \to l2\nu$ , $m_X~700\text{GeV}$

Schematic leptonic $\Sigma \to \Lambda l\nu$ , $m_X~700\text{GeV}$

The classification according to interaction energy m_X

For strong decays is as follows.

There are here 3 strong (color) decays:

Pion and eta decays, with scales $m_X\approx \left(0.3,7.5,20\right)\text{GeV}$ , mediated by a pion.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

1. 1. Chang, Y.F. (2010) Various Decays of Particles.


2. 2. Helm, J. (2019) Calculation of the Standard Model Parameters and Particles Based on a SU(4) Preon Model.


3. 3. Salam, G. (2015) SAIFR School on QCD and LHC Physics.


4. 4. Schwinn, C. (2015) Modern Methods of Quantum Chromodynamics. Universität Freiburg, Freiburg.


5. 5. Casalderrey, J. (2017) Lecture Notes on the Standard Model. University of Oxford, Oxford.


6. 6. Ho-Kim, Q. and Xuan-Yem, P. (1998) Elementary Particles and Their Interactions. Springer, Berlin. https://doi.org/10.1007/978-3-662-03712-6


7. 7. Kaku, M. (1993) Quantum Field Theory. Oxford University Press, Oxford.


8. 8. Wietfeldt, F. (2018) Atoms, 6, Article No. 70. https://doi.org/10.3390/atoms6040070


9. 9. Hayes, C.B. (2012) Neutron Beta Decay.


10. 10. Kleinert, H. (2016) Particles and Quantum Fields. World Scientific, Singapore. https://doi.org/10.1142/9915


11. 11. Serra, N. (2016) Fermi’s Golden Rule. Lecture, University of Zurich, Zürich.


12. 12. George, F. (2012) Muon & Tauon Lifetime. University of South California, Berkeley.


13. 13. Lattes, C., et al. (1947) Nature, 159, 694-698. https://doi.org/10.1038/159694a0


14. 14. Von Schlippe, W. (2002) Relativistic Kinematics of Particle Interactions. University of Utah, Salt Lake City.


15. 15. Bystritskiy, Yu.M. and Kuraev, E.A. (2005) Physical Review D, 72, Article ID: 114019. https://doi.org/10.1103/PhysRevD.72.114019


16. 16. Good, R.H., et al. (1961) Physical Review, 124, 1223-1239. https://doi.org/10.1103/PhysRev.124.1223


17. 17. Borg, F. (2005) Isospin Breaking in Kaon Decays to Pions. Thesis, Lund University, Lund.


18. 18. Jackson, J. and Tovey, D. (2000) Particle Kinematics. Particle Data Group, Berkeley.


19. 19. Quarks (2018). https://www.hyperphysics.phy-astr.gsu.edu


20. 20. Epele, L. (2002) Radiative Decays of Mesons in the NJL Model. Instituto de Fisica La Plata, La Plata.


21. 21. Yao, W.-M., et al. (Particle Data Group) (2006) Journal of Physics G: Nuclear and Particle Physics, 33, 1. https://doi.org/10.1088/0954-3899/33/1/001


22. 22. Krauss, F. (2005) Quarks and Leptons. Durham University, Durham.


23. 23. Lach, J. and Zenczykowski, P. (1995) International Journal of Modern Physics A, 10, 3817-3876. https://doi.org/10.1142/S0217751X95001807


24. 24. Aihara, H. (1986) Physical Review D, 33, 844-847. https://doi.org/10.1103/PhysRevD.33.844


25. 25. Costa, P., et al. (2004) Two Photon Decay of π0 and η.


26. 26. Butler, F., et al. (1990) Physical Review D, 42, 1368-1384.


27. 27. Greiner, W., Schramm, S. and Stein, E. (2007) Quantum Chromodynamics. Springer, Berlin.


28. 28. ‘t Hooft, G. (2008) Scholarpedia, 3, 7443. https://doi.org/10.4249/scholarpedia.7443


29. 29. Helm, J. (2021) Physics Fundamentals.


30. 30. Helm, J. (2021) Quantum Chromodynamics on Lattice: Direct Minimization of QCD-QED-Action with New Results. https://researchgate.net


31. 31. Helm, J. (2021) Standard Model of Particle Physics I. https://researchgate.net


32. 32. Helm, J. (2019) Standard Model of Particle Physics II. https://researchgate.net


33. 33. Helm, J. (2019) Code QHCDLattice.nb, QHCDLatticeResults.nb, researchgate, 2019.


34. 34. Helm, J. (2019) Code QHCDDecay.nb, QHCDDecayRes.nb, researchgate, 2019.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Chang, Y.F. (2010) Various Decays of Particles.
[2]	Helm, J. (2019) Calculation of the Standard Model Parameters and Particles Based on a SU(4) Preon Model.
[3]	Salam, G. (2015) SAIFR School on QCD and LHC Physics.
[4]	Schwinn, C. (2015) Modern Methods of Quantum Chromodynamics. Universität Freiburg, Freiburg.
[5]	Casalderrey, J. (2017) Lecture Notes on the Standard Model. University of Oxford, Oxford.
[6]	Ho-Kim, Q. and Xuan-Yem, P. (1998) Elementary Particles and Their Interactions. Springer, Berlin. https://doi.org/10.1007/978-3-662-03712-6
[7]	Kaku, M. (1993) Quantum Field Theory. Oxford University Press, Oxford.
[8]	Wietfeldt, F. (2018) Atoms, 6, Article No. 70. https://doi.org/10.3390/atoms6040070
[9]	Hayes, C.B. (2012) Neutron Beta Decay.
[10]	Kleinert, H. (2016) Particles and Quantum Fields. World Scientific, Singapore. https://doi.org/10.1142/9915
[11]	Serra, N. (2016) Fermi’s Golden Rule. Lecture, University of Zurich, Zürich.
[12]	George, F. (2012) Muon & Tauon Lifetime. University of South California, Berkeley.
[13]	Lattes, C., et al. (1947) Nature, 159, 694-698. https://doi.org/10.1038/159694a0
[14]	Von Schlippe, W. (2002) Relativistic Kinematics of Particle Interactions. University of Utah, Salt Lake City.
[15]	Bystritskiy, Yu.M. and Kuraev, E.A. (2005) Physical Review D, 72, Article ID: 114019. https://doi.org/10.1103/PhysRevD.72.114019
[16]	Good, R.H., et al. (1961) Physical Review, 124, 1223-1239. https://doi.org/10.1103/PhysRev.124.1223
[17]	Borg, F. (2005) Isospin Breaking in Kaon Decays to Pions. Thesis, Lund University, Lund.
[18]	Jackson, J. and Tovey, D. (2000) Particle Kinematics. Particle Data Group, Berkeley.
[19]	Quarks (2018). https://www.hyperphysics.phy-astr.gsu.edu
[20]	Epele, L. (2002) Radiative Decays of Mesons in the NJL Model. Instituto de Fisica La Plata, La Plata.
[21]	Yao, W.-M., et al. (Particle Data Group) (2006) Journal of Physics G: Nuclear and Particle Physics, 33, 1. https://doi.org/10.1088/0954-3899/33/1/001
[22]	Krauss, F. (2005) Quarks and Leptons. Durham University, Durham.
[23]	Lach, J. and Zenczykowski, P. (1995) International Journal of Modern Physics A, 10, 3817-3876. https://doi.org/10.1142/S0217751X95001807
[24]	Aihara, H. (1986) Physical Review D, 33, 844-847. https://doi.org/10.1103/PhysRevD.33.844
[25]	Costa, P., et al. (2004) Two Photon Decay of π0 and η.
[26]	Butler, F., et al. (1990) Physical Review D, 42, 1368-1384.
[27]	Greiner, W., Schramm, S. and Stein, E. (2007) Quantum Chromodynamics. Springer, Berlin.
[28]	‘t Hooft, G. (2008) Scholarpedia, 3, 7443. https://doi.org/10.4249/scholarpedia.7443
[29]	Helm, J. (2021) Physics Fundamentals.
[30]	Helm, J. (2021) Quantum Chromodynamics on Lattice: Direct Minimization of QCD-QED-Action with New Results. https://researchgate.net
[31]	Helm, J. (2021) Standard Model of Particle Physics I. https://researchgate.net
[32]	Helm, J. (2019) Standard Model of Particle Physics II. https://researchgate.net
[33]	Helm, J. (2019) Code QHCDLattice.nb, QHCDLatticeResults.nb, researchgate, 2019.
[34]	Helm, J. (2019) Code QHCDDecay.nb, QHCDDecayRes.nb, researchgate, 2019.