A Number Theoretic Analysis of the Enthalpy, Enthalpy Energy Density, Thermodynamic Volume, and the Equation of State of a Modified White Hole, and the Implications to the Quantum Vacuum Spacetime, Matter Creation and the Planck Frequency ()
1. Introduction
The geometric structure of quantum gravity has been established to be discontinuous and other theories of quantum gravity like loop quantum gravity consider the quantum geometry to be in the form of loops [1] while string theory considers quantum geometry to be in the form of strings [2] . We shall observe that the results of the analysis of this paper based on the work of thermodynamic constrains of a modified white hole [3] [4] encompass the form of quantum geometries as predicted by these two promising theories fundamental of physics. Precisely, it is shown that a full picture of complete quantum vacuum geometry is a combination of the two quantum geometries. A full connection of between the two quantum geometries is found through a number theoretic properties of the constraints of the thermodynamics of the modified white hole. The quantum vacuum geometry picture we found, indicates a clear depiction of the gauge bosons and the scalar bosons supergravity lattice and how they are related and arranged in relation to the graviton which through the analysis suggests that it may not be a gauge boson, but an independent quantum geometric force carrier as discussed by [5] . This then shows that in the final analysis, the quantum vacuum geometry that we derived, is fundamentally as it sheds some light of matter creations facilitated by the Higgs scalar boson from supersymmetric vacuum quantum geometry, through to symmetric breaking at the moment of big bang, and into the well know mechanism of matter formation moment after the big-bang
Our paper is structured as follows: Sections A and B, we analyse and list the number theoretic properties and the Ramanujan recurring number properties of the fundamental thermodynamic quantities of the modified white hole in the presence of a cosmological constant at extremely low entropy. Then in Section C, we apply these properties to quantum gravity and in the process we get a picture of the nature of the quantum geometry of the modified white whole in terms of octahedrons and a sphere, and we show that this quantum geometry has the properties of quantum strings and brane/Instanton. In Section D, we illustrate theoretic number connections to Planck multiple spectrum frequency and to the hypothetical Gluino mass.
SECTION A: Analysis the equations of the modified white hole enthalpy coupled to quantum Bose-Einstein condensate at extremely low entropy
The equations to be analysed in this section are from paper by [4]
2. Analysis of the Enthalpy of the Modified White Hole
The enthalpy of the modified white hole is given by
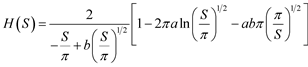 . (1)
. (1)
We analyze the number theoretic properties and the Ramanujan recurring number properties of the enthalpy Equation (1) as follows;
1) Exact result
The exact results of enthalpy Equation (1) is
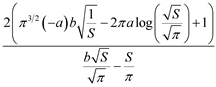 . (2)
. (2)
Which has the alternate forms;
 , (3)
, (3)
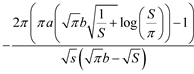 , (4)
, (4)
 . (5)
. (5)
The alternative forms Equations (3), (4), and (5) has the following expanded form
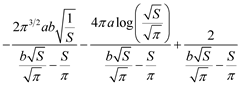 . (6)
. (6)
Assuming a, b, and S are positive, the alternative forms are
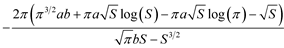 , (7)
, (7)
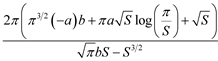 . (8)
. (8)
from which we obtain the expanded logarithmic form as
 , (9)
, (9)
and assuming that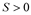 ,
, 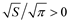 , and
, and , then we get the alternate form
, then we get the alternate form
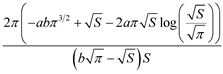 , (10)
, (10)
and the its derivative
 (11)
(11)
2) Indefinite integral
Equation (11) has the following indefinite integral
 (12)
(12)
from which we obtain the alternate forms
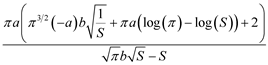 , (14)
, (14)
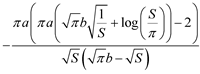 , (15)
, (15)
 (16)
(16)
Assuming a, b, and S are positive, then the alternate forms are
![]() , (17)
, (17)
![]() (18)
(18)
![]() (19)
(19)
The expanded logarithmic form of the alternate forms Equation (17), (18), and (19) are then given by
![]() (20)
(20)
and assuming that![]() ,
, ![]() , and
, and![]() , then we get the alternate form
, then we get the alternate form
![]() (21)
(21)
and then its derivative
![]() (22)
(22)
3) Indefinite integral
We obtain the indefinite integral of the Equation (22) as
![]() (23)
(23)
which has the alternative forms
![]() , (24)
, (24)
![]() , (25)
, (25)
![]() (26)
(26)
Equations (24), (25), and (26) has the expanded form
![]() (27)
(27)
and assuming a, b, and S are positive, then we obtain the alternate form
![]() (28)
(28)
which has the expanded logarithmic form
![]() . (29)
. (29)
and assuming that![]() ,
, ![]() , and
, and![]() , then we get the alternate form
, then we get the alternate form
![]() , (30)
, (30)
which has the derivative
![]() (31)
(31)
4) Indefinite integral
The indefinite integral of the Equation (31) is
![]() (32)
(32)
5) Volume analysis
Because of supersymmetry of space at extremely low entropy, then it is therefore possible to consider the vortices of the quantum vacuum schematized as cubes or octahedrons loops. We also assume that the quantum Van der Waals fluid [4] [6] are characterized by smooth spheres. In reality, the quantum vacuum will have n-dimensional hyperspheres in which the compactified dimensions “roll up” and octahedrons representing the “fluctuations”, containing vibrating quantum Van der Waals fluid particles.
Therefore, for ![]() (octahedron volume) and
(octahedron volume) and ![]() (sphere volume), where
(sphere volume), where![]() , we get the following;
, we get the following;
a) Octahedron volume
From indefinite integral Equation (32) we obtain the following exact result
![]() (33)
(33)
which has the alternative forms
![]() , (34)
, (34)
![]() , (35)
, (35)
![]() (36)
(36)
![]()
The expanded form of Equations (34), (35), and (36) is
![]() (37)
(37)
and assuming a, b, and S are positive, we obtain the alternate forms of Equation (37) as
![]() ,
,
![]() , (38)
, (38)
which has the expanded logarithmic form given by
![]() . (39)
. (39)
The alternate form of Equation (39) is
![]() (40)
(40)
and its derivative is given by
![]() (41)
(41)
The indefinite integral of Equation (41) is then given by
![]() (42)
(42)
b) Sphere volume
From indefinite integral Equation (32) we obtain the exact result
![]() (43)
(43)
which has the alternate forms
![]() , (44)
, (44)
![]() , (45)
, (45)
![]() (46)
(46)
and the expanded forms of Equations (44), (45), and (46) are given by
![]() (47)
(47)
Now assuming that a, b, and S are positive, then we obtain the alternate forms
![]() (48)
(48)
with the expanded logarithmic form
![]() . (49)
. (49)
The alternate form of Equation (49) is
![]() , (50)
, (50)
with the derivative
![]() (51)
(51)
and the indefinite integral
![]() (52)
(52)
c) Number theoretic properties of the volume
i) DN Constant
Now dividing the two indefinite integral results for the octahedron and the sphere volumes; Equation (42) and Equation (52) respectively, we get
![]() (53)
(53)
and
![]() (54)
(54)
which simplifies to the exact result
![]() (55)
(55)
of which the expanded form is
![]() (56)
(56)
with the alternative form
![]() (57)
(57)
which is a DN Constant.
ii) The property of the function
The function has an even parity
iii) Indefinite integral
![]() (58)
(58)
iv) Global maximum
![]() at
at ![]() (59)
(59)
v) Global minimum
![]() at
at ![]() (60)
(60)
vi) Limit
![]() (61)
(61)
![]() (62)
(62)
vii) Series representations
![]() (63)
(63)
for (not (![]() and
and![]() ))
))
![]() (64)
(64)
for (![]() and
and![]() )
)
![]() (65)
(65)
where ![]() is the factorial function, (a)n, is the Pochhammer symbol (rising factorial),
is the factorial function, (a)n, is the Pochhammer symbol (rising factorial), ![]() is the set of real numbers,
is the set of real numbers, ![]() is the complex argument,
is the complex argument, ![]() is the floor function, and i, is the imaginary unit.
is the floor function, and i, is the imaginary unit.
viii) Definite integral over a disk of radius R
![]() (66)
(66)
Definite integral over a square of edge length 2L
![]() (67)
(67)
3. Analysis of the Thermodynamic Volume of the Modified White Hole
The thermodynamic volume of the modified white hole is given by
![]() . (68)
. (68)
The analysis gives the following number theoretic properties and the Ramanujan recurring number properties of the thermodynamic volume:
1) Alternate forms
The thermodynamic volume Equation (68) has the following alternate forms
![]() , (69)
, (69)
![]() . (70)
. (70)
Assuming a, b, and S are positive, then the alternative forms Equations (69), and (70) becomes
![]() (71)
(71)
and the derivative is
![]() (72)
(72)
The indefinite integral is then given by
![]() (73)
(73)
Dividing the alternate form Equation (69) by
![]() (74)
(74)
we obtain the exact result
![]() . (75)
. (75)
2) Volume analysis
From the exact result Equation (75), and with ![]() (octahedron volume) and
(octahedron volume) and ![]() (sphere volume), where
(sphere volume), where![]() , we obtain respectively;
, we obtain respectively;
a) Octahedron volume:
The exact result
![]() (76)
(76)
b) Sphere volume:
The exact result
![]() (77)
(77)
3) Number theoretic properties of the volume
By dividing the two exact results Equations (76), and (77), and simplifying by making the input![]() , we get the results
, we get the results
![]() (78)
(78)
With the decimal approximation
![]()
which is a DN Constant, and also ![]() it has property that it is a transcendental number. The transcendental numbers have important properties in physics and in particular in astrophysics, particle physics, cosmology because they allow us to reformulate and resolve unresolved problems, and in our case, the geometry of quantum gravity of the very early universe [7] .
it has property that it is a transcendental number. The transcendental numbers have important properties in physics and in particular in astrophysics, particle physics, cosmology because they allow us to reformulate and resolve unresolved problems, and in our case, the geometry of quantum gravity of the very early universe [7] .
The series representation of Equation (78) is
![]() (79)
(79)
for (not (![]() and
and![]() ))
))
![]() (80)
(80)
for (![]() and
and![]() )
)
![]() (81)
(81)
4. Analysis of the Enthalpy Energy Density of the Modified White Hole
The enthalpy energy density of the modified white hole is given by
![]() (82)
(82)
and dividing the exact result Equation (2) by the alternative form Equation (69), we obtain
![]() . (83)
. (83)
Then the analysis gives the following number theoretic properties and the Ramanujan recurring number properties of the enthalpy energy density. The exact result is
![]() , (84)
, (84)
and for![]() , we obtain
, we obtain
![]() , (85)
, (85)
which has the alternate forms
![]() (86)
(86)
![]() (87)
(87)
![]() (88)
(88)
The alternate forms Equations (86), (87), and (88) have the expanded forms
![]() (89)
(89)
with the expanded logarithmic form
![]() (90)
(90)
which has the alternate form
![]() . (91)
. (91)
The root for the variable b is
![]() . (92)
. (92)
1) Indefinite integral
The indefinite integral for the alternative form Equation (91) is
![]() (93)
(93)
from which we obtain the alternate forms
![]() , (94)
, (94)
![]() , (95)
, (95)
![]() . (96)
. (96)
The expanded form of Equations (93), (94) and (95) is
![]() (97)
(97)
Assuming a, b, and S are positive, then we have the alternative form
![]() (98)
(98)
From which the expanded logarithmic form is
![]() (99)
(99)
The alternate form of the Equation (99) is
![]() , (100)
, (100)
with the roots are
![]()
![]()
![]()
![]() (101)
(101)
2) Series expansion
The Taylor series expansion about ![]() is
is
![]() (102)
(102)
and the Laurent series expansion about ![]() is
is
![]() (103)
(103)
The derivative of the alternative form, Equation (100) is
![]() (104)
(104)
With the indefinite integral given by
![]() (105)
(105)
Taking the limit of alternative form, Equation (100) as![]() , we get
, we get
![]() , (106)
, (106)
and for ![]() (octahedron volume) and
(octahedron volume) and ![]() (sphere volume), where
(sphere volume), where![]() , we obtain the following respectively;
, we obtain the following respectively;
a) Octahedron volume
For the octahedron volume we have
![]() , (107)
, (107)
and plotting this result, we obtain the following 3D and the contour plots that can be related to a D-brane/Instanton.
The key observation from Figure 1 and Figure 2 and as confirmed by [4] , is that at![]() , which is taken as the energy density of the universe at the Big bang, with
, which is taken as the energy density of the universe at the Big bang, with ![]() the zero spacetime volume, the vacuum geometry brakes/or there is symmetry breaking on the vacuum quantum geometry. We see from the plots as the vacuum spacetime break/tear apart. Continuing further, we obtained the following properties of the Equation (107), that the alternate forms are
the zero spacetime volume, the vacuum geometry brakes/or there is symmetry breaking on the vacuum quantum geometry. We see from the plots as the vacuum spacetime break/tear apart. Continuing further, we obtained the following properties of the Equation (107), that the alternate forms are
![]() , (108)
, (108)
![]() , (109)
, (109)
![]() . (110)
. (110)
The expanded forms of Equations (108), (109), and (110) are
![]() (111)
(111)
and assuming a, b, and S are positive, then we have the alternative form
![]() (112)
(112)
from which the expanded logarithmic form is
![]() (113)
(113)
with the alternate form
![]() (114)
(114)
The roots of the alternate form Equation (114) are
![]()
![]()
![]()
![]() (115)
(115)
Furthermore, the Taylor series expansion about ![]() is
is
![]() (116)
(116)
and about ![]() is
is
![]() (117)
(117)
The derivative of the alternate form Equation (113) is
![]() (118)
(118)
and the indefinite integral is
![]() (119)
(119)
b) Sphere volume
For the octahedron volume we have
![]() , (120)
, (120)
And similarly plotting this result, we obtain the following 3D and the contour plots that can be related to a D-brane/Instanton.
The observation in Figure 3, and Figure 4, is the same as in Figure 1, and Figure 2. Continuing further, we obtained the following properties of the Equation (120), that the alternate forms are
![]() , (121)
, (121)
![]() , (122)
, (122)
![]() (123)
(123)
from which the expanded forms are
![]() (124)
(124)
Assuming a, b, and S are positive, the alternative forms are
![]() (125)
(125)
and thus the expanded form is
![]() (126)
(126)
from which the alternate form is
![]() (127)
(127)
with the roots
![]()
![]()
![]()
![]() . (128)
. (128)
The Taylor series expansion about![]() , is
, is
![]() (129)
(129)
and about![]() , is
, is
![]() (130)
(130)
The derivative of the alternate form Equation (127)
![]() (131)
(131)
and the indefinite integral is
![]() (132)
(132)
c) The ratio of the Octahedron volume to the sphere volume and its number theoretic properties
Taking the limit
![]() , (133)
, (133)
and thus, dividing Octahedron volume Equation (107) by the Sphere volume Equation (120), and simplifying by the factor
![]() (134)
(134)
we obtained
![]() (135)
(135)
with decimal approximation
![]()
(which is DN Constant, and it is also a transcendental number as well). It has the following series representations
![]() (136)
(136)
for (not (![]() and
and![]() ))
))
![]() (137)
(137)
for (![]() and
and![]() )
)
![]() (138)
(138)
5. Analysis of the Equation of State of the Modified White Hole
The equation of state of the modified white hole is given by
![]() (139)
(139)
The analysis gives the following number theoretic properties and the Ramanujan recurring number properties of the equations of state:
The exact result is
![]() (140)
(140)
and considering![]() , we obtain V to be
, we obtain V to be
![]() , (141)
, (141)
which then simplifies to
![]() , (142)
, (142)
which when we plot it, get the 3D and the contour plots below that can be related to a D-brane/Instanton,
From Figure 5, and Figure 6, we note that the gravitational potential is almost zero as the self vacuum perturbations have not started to take effects resulting in the flat quantum vacuum geometry. The alternate forms of Equation (142) are
![]() (143)
(143)
![]() (144)
(144)
![]() (145)
(145)
which have the expanded logarithmic form
![]() (146)
(146)
1) number theoretic properties of the equation of state
a) Roots
From which the alternate form
![]() (147)
(147)
and the roots are
![]()
![]() (148)
(148)
![]() (149)
(149)
The polynomial discriminant is
![]() , (150)
, (150)
and the integer root are
![]() (151)
(151)
Thus the derivative of the alternative form Equation (147) is
![]() (152)
(152)
b) Indefinite integral
The indefinite integral is
![]() (153)
(153)
which when we plot it, get the 3D plot that can be related to a D-brane/Instanton, and we also plot its contour plot
From Figure 7, and Figure 8, we also observe that the vacuum quantum geometry starts to be uneven, meaning the seeds for the gravitational potential are starting to take effects due to the self-perturbations starting to take effect.
The alternate forms of indefinite integral Equation (153) is
![]() (154)
(154)
![]() (155)
(155)
![]() (156)
(156)
and assuming a, b, and S are positive, then we have the alternative form
![]() , (157)
, (157)
from which the expanded logarithmic form is
![]() . (158)
. (158)
From the expanded logarithmic form, Equation (158), the alternative form is
![]() (159)
(159)
With the root
![]()
![]()
![]() (160)
(160)
The polynomial discriminant is
![]() (161)
(161)
and the derivative is
![]() (162)
(162)
with the indefinite integral
![]() (163)
(163)
From the above indefinite integral, we have the following 3D and the contour plots that can be related to a D-brane/Instanton,
From Figure 9, and Figure 10, we also observe that the vacuum quantum geometry starts to be more uneven that that in Figure 7 and Figure 8. That is, the gravitational potential of the quantum vacuum geometry is growing, as a result of the growth of the vacuum self-perturbations.
The alternate forms of the indefinite integral Equation (163) are
![]() (164)
(164)
![]() (165)
(165)
![]() (166)
(166)
and assuming a, b, and S are positive, then we have the alternative form
![]() . (167)
. (167)
The expanded logarithmic form of Equation (167) is
![]() (168)
(168)
and the alternate form is
![]() , (169)
, (169)
with the root
![]()
![]()
![]() . (170)
. (170)
The polynomial discriminant is![]() , and the derivative of the alternate form Equation (169) is
, and the derivative of the alternate form Equation (169) is
![]() (171)
(171)
and the indefinite integral is
![]() (172)
(172)
The local minimum is
![]()
at
![]() (173)
(173)
In conclusion, the indefinite integral result Equation (172), and for ![]() (octahedron volume) and
(octahedron volume) and ![]() (sphere volume), where
(sphere volume), where![]() , we obtain:
, we obtain:
1) Octahedron volume
For the octahedron we have
![]() (174)
(174)
which when we plot it, get the 3D and the contour plots that can be related to a D-brane/Instanton
From Figure 11, and Figure 12, we now observe that the vacuum gravitational potential has grown exponentially and infinitely high as a results of the exponentially grown and infinitely high growth vacuum self-perturbations near a = 1, i.e. the energy density of the universe at the big bang.
The alternate forms were found to be
![]() (175)
(175)
![]() (176)
(176)
![]() (177)
(177)
and the expanded form is
![]() (178)
(178)
with the expanded logarithmic form
![]() (179)
(179)
The alternate form of Equation (179) is
![]() (180)
(180)
With the root
![]()
![]()
![]() . (181)
. (181)
The polynomial discriminant is![]() , and the derivative is
, and the derivative is
![]() (182)
(182)
and the indefinite integral
![]() (183)
(183)
The local minimum is
![]()
at
![]() (184)
(184)
2) sphere volume
For the sphere we have
![]() (185)
(185)
Which when we plot it, get the 3D plot that can be related to a D-brane/Instanton, and we also plot its contour plot
As in Figure 13, and Figure 14 in case of the octahedron, here, we also observe that the vacuum gravitational potential has grown exponetially and infinittely high as a results of the exponentially grown and infinitely high growth vacuum self-perturbations near a = 1, i.e. the energy density of the universe at the big bang.
The alternate forms of Equation (185) are
![]() (186)
(186)
![]() (187)
(187)
![]() (188)
(188)
and assuming a, b, and S are positive, then we have the alternative form
![]() , (189)
, (189)
from which the expanded logarithmic form is
![]() . (190)
. (190)
The alternative form of the expanded logarithmic form E. (193)
![]() (191)
(191)
with the root
![]()
![]()
![]() . (192)
. (192)
The polynomial discriminant is![]() , and the derivative is
, and the derivative is
![]() (193)
(193)
From the indefinite integral is
![]()
at
![]() , (194)
, (194)
By dividing the integral Equation (183) with the integral Equation (194), we obtain the result
![]() (195)
(195)
With the decimal approximation
![]()
(which is a DN Constant and also a transcendental number). It is also the reduced logarithmic form. The alternative representations are
![]() (196)
(196)
![]() (197)
(197)
![]() (198)
(198)
where ![]() is the base b logarithm,
is the base b logarithm, ![]() is the polylogarithm function
is the polylogarithm function
1) Series representations
![]() (199)
(199)
for (not (![]() and
and![]() ))
))
![]() (200)
(200)
for (not (![]() and
and![]() ))
))
![]() (201)
(201)
for (![]() and
and![]() )
)
![]() (202)
(202)
SECTION C: On the application of the formulas of the volumes of an octahedron and a sphere to quantum gravity
In this section we apply the number theoretic properties and the Ramanujan recurring number properties to the quantum geometry of the white hole. With regard to a sphere inscribed in an octahedron, we have the following formulas.
![]() ,
, ![]() where
where ![]() (203)
(203)
We take the ratio between the two above formulas for the octahedron and sphere in Equation (203) as shown in Figure 15
![]() , (for
, (for![]() ) (204)
) (204)
with the decimal approximation,
![]() (205)
(205)
(which is a DN Constant, and a transcendental number)
The series representations Equation (204)
![]() (206)
(206)
for (not (![]() and
and![]() ))
))
![]() (207)
(207)
for (![]() and
and![]() )
)
![]()
Figure 15. Sphere inscribed in an octahedron.
![]() (208)
(208)
from which we obtain
![]() , (209)
, (209)
with the decimal approximation
![]() (210)
(210)
(which is the trace of the instanton shape and Ramanujan Recurring Number, and it is also a transcendental number).
The series representations of Equation (209) are
![]() , (211)
, (211)
![]() (212)
(212)
![]() , (213)
, (213)
with the integral representations
![]() (214)
(214)
![]() (215)
(215)
![]() (216)
(216)
We note that, from the sum of the first nine numbers excluding 0, i.e., ![]() (these are the fundamental numbers, from which, through infinite combinations, all the other numbers are obtained), we obtain the following interesting formula:
(these are the fundamental numbers, from which, through infinite combinations, all the other numbers are obtained), we obtain the following interesting formula:
![]() (217)
(217)
where ![]() is the golden ratio,
is the golden ratio, ![]() is the MRB constant. The exact result of Equation (217) is then given by
is the MRB constant. The exact result of Equation (217) is then given by
![]() , (218)
, (218)
With the decimal approximation
![]() (219)
(219)
(which is a trace of the instanton shape and Ramanujan Recurring Number)
The alternate forms for Equation (218) is
![]() , (220)
, (220)
![]() , (221)
, (221)
![]() , (222)
, (222)
From which the expanded forms are
![]() , (223)
, (223)
![]() , (224)
, (224)
and making input
![]() , (225)
, (225)
then we get exact results
![]() (226)
(226)
with the decimal approximation
![]() (227)
(227)
(which is a Ramanujan Recurring Number)
The alternate form of Equation (226) is
![]() , (228)
, (228)
![]() , (229)
, (229)
from which the expanded forms are
![]() , (230)
, (230)
![]() . (231)
. (231)
All 2nd roots of ![]() are
are
![]() (232)
(232)
(real, principal root)
![]() (233)
(233)
(real root).
Furthermore, form the input:
![]() , (234)
, (234)
where value 8 is linked to the “Ramanujan function” (an elliptic modular function that satisfies the need for “conformal symmetry”) that has 8 “modes” corresponding to the physical vibrations of a superstring.
The series representations Equation (234) are
![]() (235)
(235)
for (not (![]() and
and![]() )),
)),
![]() (236)
(236)
for (![]() and
and![]() )
)
![]() (237)
(237)
And by the input
![]() (238)
(238)
The value 24 is linked to the “Ramanujan function” (an elliptic modular function that satisfies the need for “conformal symmetry”) that has 24 “modes” corresponding to the physical vibrations of a bosonic string representing a bosons. From the analysis, we observe that there is no number theoretic connection with physical vibrations of fermionic strings at extremely low entropy. This fact is confirmed by the fact that the Higgs bosons at the moment of the big bang and infinitesimally shortly thereafter, facilitated the creation of fermions (matter and antimatter particles) [8] . Thus we note that the ingredients for the formation of electromagnetic radiation from photons (a Boson), and the formation of matter from the Higgs boson after the big bang, are intrinsic properties of the vacuum energy in pre big bang.
The series representations are
![]() (239)
(239)
for (not (![]() and
and![]() )),
)),
![]() (240)
(240)
for (![]() and
and![]() ),
),
![]() (241)
(241)
By the input
![]() . (242)
. (242)
The number 4096 = 642, is the Ramanujan Recurring Number, that when multiplied by 2 give 8192. The total amplitude vanishes for gauge group SO (8192) for bosonic string SO (8192), while the vacuum energy is negative and independent of the gauge group. The vacuum energy and dilaton tadpole to lowest non-trivial order for the open bosonic string. While the vacuum energy is non-zero and independent of the gauge group, the dilaton tadpole is zero for a unique choice of gauge group, SO (213) i.e. SO (8192), [9] . This could be the implications for a pre-big bang scenario where only self-perturbative bosonic strings lived when the enthalpy was extremely low as discussed above. This regime contains all the intrinsic properties of superstrings inherent in the bosonic strings that as observed by [10] , (2006), would at the big bang give effect to the properties of matter (fermions) as Higgs Boson. This number theoretic connection to the gauge group SO (8192), gives a much more compelling relevance of the bosonic string theory SO (8192), to quantum gravity and places this string theory where it should appropriately be in the evolution of the universe from a quantum gravity perspective rather than it be neglected because it doesn’t include fermionic strings to confirm to post big-bang reality. The vanishing of the bosonic string’s amplitude could be explained by the effect of extreme low entropy on the quantum vacuum geometry as discussed in [4] . Thus, as the entropy increases infinitesimally as a result of the vacuum self-perturbation then also is the amplitude of the vibrating bosonic strings from zero. [9] was right to indicate that the “vanishing of the amplitude of the bosonic string could be the results of string theory itself”, but here, we give a much more elaborate explanation of what could be happening.
We further proceed and make the input
![]() (243)
(243)
This result is very near to the mass of candidate glueball ![]() scalar meson. Furthermore, 1728 occurs in the algebraic formula for the j-invariant of an elliptic curve
scalar meson. Furthermore, 1728 occurs in the algebraic formula for the j-invariant of an elliptic curve![]() . The number 1728 is one less than the Hardy-Ramanujan number 1729 (taxicab number, as it can be expressed as the sum of two cubes in two different ways
. The number 1728 is one less than the Hardy-Ramanujan number 1729 (taxicab number, as it can be expressed as the sum of two cubes in two different ways ![]() and Ramanujan’s recurring number). Since bosons are made of gauge bosons and scalar bosons (meson), then this number theoretic analysis perhaps confirm that the number 1729, confirm the fact that both the gauge and scalar bosons are actually different states of a single bosonic string, and that these states are isomorphic or that the states vibrations are synchronised with the state of the bosonic string. This also implies that each state lives inside a cubic or octahedron as a spherical cloud, and that the total sum of these two states is the state of the bosonic string. Taking the cross section of the bosonic string, we realise that it must be a rectangular, or a two shaped octahedron. As the string vibrates in difference frequencies, so is the two spherical cloud states inside the string. That is, the string vibrations simply excites the gauge bosons i.e. Photon, gluon, W and Z inside one cube/octahedron, and the scalar boson i.e. Higgs inside the other cube/octahedron.
and Ramanujan’s recurring number). Since bosons are made of gauge bosons and scalar bosons (meson), then this number theoretic analysis perhaps confirm that the number 1729, confirm the fact that both the gauge and scalar bosons are actually different states of a single bosonic string, and that these states are isomorphic or that the states vibrations are synchronised with the state of the bosonic string. This also implies that each state lives inside a cubic or octahedron as a spherical cloud, and that the total sum of these two states is the state of the bosonic string. Taking the cross section of the bosonic string, we realise that it must be a rectangular, or a two shaped octahedron. As the string vibrates in difference frequencies, so is the two spherical cloud states inside the string. That is, the string vibrations simply excites the gauge bosons i.e. Photon, gluon, W and Z inside one cube/octahedron, and the scalar boson i.e. Higgs inside the other cube/octahedron.
Furthermore, if we bring the picture of loop quantum gravity (LQG) with the property of a discontinuous quantum geometry, we can therefore, think of the graviton living on the vertices of the rectangles or the octahedrons. This graviton then acts a glue binding the bosonic strings lattice together forming a complete cross section of alternating states of between the gauge bosons and scalar bosons. This arrangement of states then gives a precise supersymmetric quantum picture of the vacuum geometry at low entropy.
But the geometry further reveal very important fact, that since the vacuum geometry is discontinues, then we observe that there is no relation whatsoever between the quantum vibrational frequencies of the strings, and that of the vertices of the vacuum geometry where the graviton lives. Ashtekar et al., (2021) asserted that gravity is simply a manifestation of spacetime geometry. Thus, the graviton cannot be a string boson, however, there is a duality between gravity and strings [11] . Also, gauge bosons have spin-1, while the graviton has spin-2. Then lastly, because of the thermodynamic constraints we were able to arrive at the results we have, now this bring us to this fundamental question; that string theory and LQG theory are two intrinsic aspects of a complete quantum gravity theory we are after? That is, without the other no complete and compelling quantum geometry can be attained, as it is done here? This needs to be investigated further.
The series representations of Equation (243) are
![]() , (244)
, (244)
![]() , (245)
, (245)
![]() . (246)
. (246)
We input
![]() , (247)
, (247)
With a decimal approximation
1.61805555555555555555555555555555555555555555555555555555555555, (248)
Which is the result that is a very good approximation to the value of the golden ratio 1.618033988749… (which is a Ramanujan Recurring Number). The 1.61805 is the repeating decimal.
The series representations
![]() (249)
(249)
for (not (![]() and
and![]() )),
)),
![]() (250)
(250)
for (![]() and
and![]() )
)
![]() (251)
(251)
From inputting the transcendental number Equation (233), we obtain:
![]() , (252)
, (252)
with the decimal approximation
![]() (253)
(253)
(which is a transcendental number).
All 2nd roots of ![]() are
are ![]() (real, principal root),
(real, principal root), ![]() (real root). Thus the series representations of Equation (252) are
(real root). Thus the series representations of Equation (252) are
![]() , (254)
, (254)
![]() , (255)
, (255)
![]() . (256)
. (256)
The integral representations are
![]() , (257)
, (257)
![]() (258)
(258)
![]() (259)
(259)
It is plausible to hypothesize that π and φ, in addition to being important mathematical constants, are constants that also have a fundamental relevance in the various sectors of Theoretical Physics and Cosmology
From![]() , we obtain:
, we obtain:
![]() (260)
(260)
With the decimal approximation
![]()
(which is the DN Constant, and a transcendental number).
All 2nd roots of ![]() are
are ![]() (real, principal root), and
(real, principal root), and ![]() (real root). The series representations of Equation (260) are
(real root). The series representations of Equation (260) are
![]() (261)
(261)
![]() (262)
(262)
for (not (![]() and
and![]() )),
)),
![]() (263)
(263)
for (![]() and
and![]() )
)
Section B: Number connections to the Planck multipole spectrum frequency and to the hypothetical Gluino mass
We note that, from the number 8, we obtain as follows:
![]() ,
, ![]() ,
, ![]() , (True)
, (True)
![]() ,
, ![]() ,
, ![]() , (True)
, (True)
![]() ,
, ![]()
From Figure 16, we notice how from the numbers 8 and 2 we get 64, 1024, 4096 and 8192, and that 8 is the fundamental number. In fact 82 = 64, 83 = 512, 84 = 4096. We define it “fundamental number”, since 8 is a Fibonacci number, which by rule, divided by the previous one, which is 5, gives 1.6, a value that tends to the golden ratio, as for all numbers in the Fibonacci sequence
Finally we note how 82 = 64, multiplied by 27, to which we add 1, is equal to 1729, the so-called “Hardy-Ramanujan number”. Then taking the 15th root of 1729, we obtain a value close to ζ(2) that 1.6438…, which, in turn, is included in the range of what we call “golden numbers”
Furthermore for all the results very near to 1728 or 1729, adding 64 = 82, one obtains values about equal to 1792 or 1793. These are values almost equal to the Planck multiple spectrum frequency (Black Body Radiation) 1792.35 and to the hypothetical Gluino mass.
Acknowledgements
We would like to thank Professor Augusto Sagnotti theoretical physicist at Scuola Normale Superiore (Pisa-Italy) for his very useful explanations and his availability