Internal Merge: Why Does It Work This Way? A Matrix Syntactic Approach to Argument Chain

Koji Arikawa

Department of English and International Cultural Studies, Momoyama Gakuin (St. Andrew’s) University, Osaka, Japan.

DOI: 10.4236/ojml.2022.123025                

Abstract

The computational processes of natural human language (C_HL) form a physical object. The first axiom of matrix syntax (MS), which investigates linguistic structures on the complex plane using quantum mechanics-based mathematical tools, converts the [±N] and [±V] values of the Chomsky matrix to [±1] and [±i]. This study analyzes the potential developments of this axiom, which has been used previously for raising examples and to describe the grammaticality algebraically. Matrix calculations were performed on elaborate geometries of grammatical and ungrammatical raising examples. Standard analysis based on the minimal computation (MC) principle of the minimalist program (MP) is on the correct track, but it can be combined with mathematical analysis to answer a fundamental question: Why does the internal merge create argument chains (A-chains) in this way, and not in other logically possible ways? With the context-sensitivity hypothesis in MP, MS provides a new perspective on A-chains. Results indicate that a chain-forming geometry contains three areas with distinct growth factors: 1) occurrences (i.e., syntactic contexts of chain members) with a constant rate; 2) backbone-structure building with an exponential rate (i.e., larger φ ~ 1.618), and 3) superposed chain-member copies with a diminishing rate (i.e., little φ ~ -0.618 or σ₁ = 0.7071). The MP-MS collaboration is a viable approach to the structure-building dynamics of C_HL and approaches linguistic physics.

Keywords

Context Sensitivity, Fibonacci Numbers, Internal Merge, Matrix Syntax, Minimalist Program, Quantum Mechanics, Superposition

1. Introduction: How Matrix Syntax Can Collaborate with Minimalist Program

The principle of minimal computation (MC; perform efficient computations) (Chomsky, 2005) is a fundamental guideline of the minimalist program (MP) (Chomsky, 1995). The MC includes, for example, the shortest move constraint (SMC) (Chomsky & Lasnik, 1993), no procrastination (Chomsky, 1995: chap. 3), Greed containing last resort (LR) principle (Chomsky, 1986a; Chomsky, 1995): Move raises α only if morphological properties of αitself would not otherwise be satisfied in the derivation (Chomsky, 1995: 261); italics added by the author; move α whenever it is possible to eliminate (check off) uninterpretable features (uF; φ (person, number, gender) and case) in α, no look-ahead (Chomsky, 2000), goal-accessibility restriction (i.e., phase impenetrability condition (PIC) (Chomsky, 2000: 108; Chomsky, 2001: 13-14).¹ Let us consider (1).

(1) a. Alice seems to like Bob.

b. * Alice seems that it is certain to like Bob.

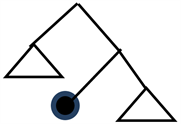
Example (1a) is a grammatical A-internal merge (A-IM), whereas (1b) is an ungrammatical A-IM, namely, a “super-raising”.² Let us assume that (1a) and (1b) have structures as shown in Figure 1 and Figure 2, respectively, where indexes are added for clarity, and waved lines indicating parts that are externalized by the sensorimotor (SM) system, i.e., pronounced.

Let us assume, with certain modifications, the essence of a probe-goal mechanism (Chomsky, 2000, 2001). In more detail, unlike the standard assumption, I assume that DP φs are uFs because they are arbitrary and lack natural (e.g., biological) bases.³ Therefore, I do not adopt a valuation, where DP φs value probe-uFs and remain. Let capital letters indicate probe-features, and small letters goal-features.

In (1a), Alice₀ is externally merged at vP edge and assigned a θ role [experiencer]. The probe uF [NULL] (null case) in the embedded-clause tense head T1 (infinitival to) attracts the closest goal Alice₀ containing a matching uF [null] (Chomsky & Lasnik, 1993; Martin, 2001), which obeys PIC. [NULL] and [null] match and delete. Note that [3, sg] in Alice₀ is still present. The matrix-clause tense head T2 (a suffix s) bears a probe uF [III, SG], which attracts the closest goal Alice₁ bearing matching uF [3, sg] to the TP2 edge, obeying PIC. The T2-probe uF [III, SG] and uF [3, sg] in all Alice copies are eliminated because

Figure 1. Phrase structure of (1a).

Figure 2. Phrase structure of (1b).

they match. Every [3, sg] in every Alice copy is deleted since the same thing happens in every copy, i.e., the same entity. The nominative case [nom] in Alice₀ disappears as a side-effect of φ elimination.⁴ Importantly, by the end of the derivation, each of the three Alice copies has the same θ role, containing no uF. Each probe attracts the closest goal, obeying PIC, in (1a).

One might ask a fundamental question. If IM is motivated by the need to check and value features, then how is it possible that a chain contains identical members? Will the lowest link in the chain always have more uninterpretable features than the highest link? Does enforcing identity defeat the whole purpose of movement in the MP? I do not adopt the valuation, which causes a significant complication. All copies are identical at the final derivation step if all uFs in probes and goals eliminate via matching without valuation.

Let us consider (1b). The same algorithm applies until the matrix tense T3 externally merges with VP3, except that an expletive it externally merges with T2'. The T3-probe [III, SG] attempts to attract the closest goal that has matching φ [3, sg]. The T3-probe cannot attract the expletive it because it is frozen at the TP2 edge. If T3-probe attracted it forcefully, the output is ungrammatical: * It seems that is certain to like Bob. Given PIC-I, T3-probe can see C1 (that) and CP1 edge (none) only. That is, there is nothing T3-probe can attract. If an “expletive-support” (like do-support) is invoked as an LR, i.e., fetch an expletive from the lexicon and externally merge it at TP3 edge, the output is grammatical: It (there) seems that it is certain for Alice to like Bob, where a preposition for is inserted as an LR to eliminate uF in Alice₁. However, the relevant derivation chose to attract a distant Alice₁, which is already transferred to CI and SM and invisible to T3-probe, thereby violating PIC-I. Alternatively, Alice₁ skipped a potential landing site, i.e., TP2 edge. If no expletive existed and Alice₁ managed to reach TP2 edge, the output is grammatical: Alice seems to be certain to like Bob.

A point to be elaborated regarding (1a; Figure 1) is as follows. The occurrences (i.e., syntactic contexts) of Alice copies are v’, T1’, and T2’. They are distinct. Why do the same copies appear in different contexts? Suppose that the T2-probe [III, SG] attracted externally-merged Alice₀ in Figure 1, which obeys PIC because no strong phase intervenes between TP2 and vP. Why can Alice₀ not move to the TP2 edge? Furthermore, we cannot distinguish whether Alice₁ or Alice₀ has undergone IM, i.e., either externalization ends up “Alice seems to like Bob.” Therefore, we cannot tell which copy has undergone an IM by just by looking at (1a), given PIC.

A part to be sophisticated regarding (1b; Figure 2) is the following. The occurrences of internally-merged Alice copies are T1’ and T3’. The occurrence of externally-merged expletive it is T2’. The syntactic contexts of internally-merged Alice copies and expletive it are the same: T’. Why can Alice and it not appear in the same context? The probe uFs [III, SG] in T2 (finite tense to which a copula be is adjoined) are eliminated when they match with the goal uFs [3, sg] in the expletive it and its case [nom] is deleted as a side-effect of φ-elimination. Assume PIC-II. When T3-probe starts searching a matching goal, the strong phase CP2 is not formed yet. Furthermore, no strong phase intervenes between CP1 and TP1. Therefore, T3-probe should be able to see Alice₁ and attract it. Why is it impossible? In contrast, the stricter PIC-I correctly bars T3-probe from attracting Alice₁. Given the Greed-LR principle, why can Alice₁ not move to the TP3 edge to eliminate its uF? Why is a Greed-LR unavailable given that it is another MP guideline? Why does PIC-I override the Greed-LR principle?

Furthermore, Martin et al. (2019: 29) asked fundamental questions regarding (1a). Why are all copies not pronounced/interpreted? Why is it the case that no more than one copy is available for interpretation at CI and for externalization at SM? Why do the objects behave that way, and not in other equally rational ways (all copies are interpreted, some copies are interpreted, …)?⁵ The MC account has explanatory power, but it can be collaborated with matrix syntax (MS), which uses mathematical tools employed in quantum mechanics (QM), to find a key to solve a hard problem (2), which is the fundamental question of the MS.

(2) Fundamental question of MS (Orús et al., 2017: 22).

What does it mean for such occurrences (i.e., syntactic contexts such as v', T1', T2' in Figure 1) to be a way to distribute an item like Alice over a phrase marker?

This paper offers a fresh look at the grammaticality of (1a) and (1b), using tools of the MS.⁶ When we investigate a chain, it is important to consider the occurrences of chain members because the occurrences are the syntactic contexts in which those member copies are allowed (1a) or disallowed (1b).⁷ Significantly, the MP has started to recast crucial concepts such as EPP, IM (movement), and phase in terms of context-sensitivity: “the status of X … changes depending on the syntactic contexts in which X occurs (Bošković, 2013, 2014). This study investigates a mathematical property of dynamics of chain-member copies (subsection 4.1) and the occurrences (syntactic contexts) of grammatical and ungrammatical raising examples (subsection 4.2). It attempts to find a clue to solve a difficult problem as (2).

This topic was chosen to enhance MP and science cooperation. The MP is a linguistic foundation of the MS, which employs QM tools. Orús et al. (2017: 3) explains why MS can be a crucial perspective: “We are not claiming to have discovered quantum reality in language. The claim, instead, is that our model of language, which we argue works more accurately and less stipulatively than alternatives, especially in providing a reasonable explanation of the behavior of chains, turns out to present mathematical conditions of the sort found in quantum mechanics. In our view, this is quite striking and merits public discussion.” The MS cooperates with MP to investigate a question (2) posed in Martin et al. (2019: 29). The MS uses the same mathematical tools as QM, the most successful physics framework to date. I believe that QM provides “more general tools to handle information” (Sato & Matsushita, 2007: 151) than just algorithms that investigate the behavior of electrons and photons. The MS should be able to provide a new perspective on the algorithms created by nature since the language system is a natural (physical) object that evolved in the human brain. More importantly, as Uriagereka (2019) stated, an MS approach enables us to perform a rigorous argument that can efficiently prove correct or incorrect based on simple mathematics.

This work is organized as follows. In Section 2, we introduce theoretical assumptions and experimental apparatus. In Section 3, we summarize our results. In Section 4, we discuss the fundamental question of MS, and propose mathematical images of a chain. The conclusion is presented in Section 5. Appendix A introduces a formal toolkit that is assumed in MS. Appendices B and C present matrix calculation of structure building of (1), which is the base of the argument in Sections 3 and 4.

2. Methods

2.1. MS

2.1.1. Axiom 1: The Fundamental Assumption of MS

Chomsky (1974) made a breakthrough when he used the distinctive features proposed by Jakobson and Halle (1971) to classify four parts of speech (adjective (A), verb (V), noun (N), and adposition (P). Table 1 shows the Chomsky matrix, where [N] represents nominal properties and [V] verbal properties; both N and V are “conceptually orthogonal” (Orús et al., 2017: 17). As Orús et al. (2017: 9) reminds the reader, “[i]t is important not to confuse the lexical attribute V with the lexical category V (which has the lexical attribute V in the positive and the lexical attribute N in the negative).”

Another breakthrough represented by MS (Uriagereka, 2016; Orús et al., 2017: 22; Martin et al., 2019), which attempts to connect C_HL with QM; MS expresses Chomsky’s matrix using the complex number z = a + bi, by translating [N] into the real number 1 and [V] into the imaginary number i.⁸ In more detail, the numerical translations are A = 1 + i,N = 1 − i,V = −1 + i, and elsewhere category = −1 – i. I adopt Orús et al. (2017: 7), where P in Chomsky matrix is replaced by elsewhere category, although I use P as a mnemonic aid for elsewhere category. The fundamental assumption of MS is (3) (Orús et al., 2017: 7), Martin et al., 2019: 31).⁹

(3) Axiom 1 (fundamental assumption)

Lexical features take the values N = 1 and V = i.

Table 1. Chomsky matrix.

We can restate the Chomsky matrices (Chomsky, 1974) as shown in (4).

(4) Axiom 2 (Chomsky matrices)

The four lexical categories are equivalent to diagonal matrices

$\text{N}=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]$ , $\text{V}=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]$ , $\text{A}=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]$ , elsewhere = $\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]$

Any structure building in any system must start somewhere. The standard assumption in MP is that a structure building proceeds bottom up in C_HL. MS postulates that the starting point is a noun and that only nouns self-merge (Axiom 6 (Guimarães))¹⁰, a compound of which is a cognitive anchor in C_HL.

Thus, $\text{N}\times \text{N}=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\cdot \left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]=\text{NP}=\text{Z}$ , i.e., one of the Pauli

matrices, which is the most elegant matrix.¹¹ MS introduces the Jarret graph (Figure 3), indicating how phrases (nodes, e.g., NP and VP) are connected through operators (edges, e.g., $\text{<mover accent="true"> <mi> N </mi> <mo> ^ </mo> </mover>}$ and $\text{<mover accent="true"> <mi> v </mi> <mo> ^ </mo> </mover>}$ ) by matrix multiplication (first merge).¹² The determiner (det) of each twin (plus and minus) node is also

shown as well, e.g., the twins $\pm \text{NP}=\pm \left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$ have the determiner det = −1.

MS claims that a phrase det is the phrase label.

For instance, an operator (function) $\text{<mover accent="true"> <mi> v </mi> <mo> ^ </mo> </mover>}$ acts on (undergoes external merge (EM) with) an NP (input) and outputs VP. More elaborately, an operator $\text{<mover accent="true"> <mi> v </mi> <mo> ^ </mo> </mover>}=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]$ acts on NP, i.e.,

$\text{<mover accent="true"> <mi> v </mi> <mo> ^ </mo> </mover>}\times \text{NP}=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\cdot \left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]=-\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\text{VP}$ , the twin of which is $\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\text{VP}$ . Thus, the det of VP is i.

One might argue against the current analysis that employs the Chomsky matrix, too simple. One might criticize that for an approach that aims at explanation,

Figure 3. Jarret graph.

the basis of the system remains deeply stipulative. One might point out that MS faces criticisms of the Chomsky matrix for its excessive rigidity and empirical inadequacies, which is a step back in linguistic research.

Regarding P, I strictly adopt Orús et al. (2017: 7) here, which names [−N, −V] output as elsewhere category. I admit that the Chomsky matrix is simple, i.e., a sentential structure containing functional elements such as light verb v, tense T, and complementizer C cannot be captured by only four categories. In fact, Orús et al. (2017: 27-32) mentioned possible matrices for functional elements.¹³ However, I want to limit this analysis to the smallest possible set, which Orús et al. (2017: 17-18) calls G₈ (the “magnificent eight” group) as shown in (5) (ibid., 18).

(5) ${\text{G}}_8=\left\{\pm I,\pm \text{Z},\pm {\text{C}}_1,\pm {\text{C}}_2\right\}$ , where

$I=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$ , $\text{Z}=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$ , ${\text{C}}_1=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]$ , ${\text{C}}_2=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]$ .

The subsets $\left\{\pm I,\pm \text{Z}\right\}$ are from the Pauli group (Hermitian), and $\left\{\pm {\text{C}}_1,\pm {\text{C}}_2\right\}$ are Chomsky matrices (non-Hermitian), which have complex entries on the diagonal. G₈ is “abelian (commutative) because all matrices are diagonal and therefore mutually commute [ $x\circ y=y\circ x$ ] (ibid.)”.¹⁴ I limit the building-block matrices to G₈ because (a) it is consistent with the strong minimalist thesis (SMT), i.e., C_HL must provide the simplest possible solutions to legibility problems, (b) G₈ “allows us to explain the basic features of the MS model” (ibid.), and (c) it is cost effective to integrate T (suffix) and C into elsewhere. Although this is a preliminary analysis that can only accommodate the most basic tools, I admit that in the future, I will need to investigate and elaborate on the tools and system.

The linear-algebraic Chomsky matrices are diagonal and eigenvalue matrices Λ that have eigenvalues λ₁ and λ₂ on their diagonal.¹⁵ In all cases, λ₁ fixes its eigenvector s₁ = (1, 0), and λ₂ determines its eigenvector s₂ = (0, 1). The four lexical categories have an eigenvalue either λ =i or λ = −i, indicating that they share a rotational property: the unit 90˚-rotation matrix Q. A and N have an eigenvalue λ = 1, which suggests that A, N, and the projection matrix share a property of perfect symmetry, i.e., everything is left unchanged. V and elsewhere category have an eigenvalue λ = −1, which shows that a reversion property characterizes them.

2.1.2. Chain Vector as Superposition

“An image is a large matrix of grayscale values, one for each pixel and color. When nearby pixels are correlated (not random) the image can be compressed (Strang, 2016: 364).” A linguistic structure is similar to a large matrix that can be compressed by correlating nearby nodes. We calculated matrices on chain (CH) structures that are created by IMs using the matrix method proposed by Orús et al. (2017) and Martin et al. (2019). They proposed that a CH is mathematically isomorphic to superposition in QM. See Appendix A for a formal toolkit that assumed in MS. The CH for Alice in (1a) is expressed in Equation (1), where v', T1', and T2' are the occurrences (i.e., syntactic contexts) in which Alice appears. SM externalizes Alice₂.

$CH=\left(\left(Alic{e}_0,v^{\prime }\right),\left(Alic{e}_1,T{1}^{\prime }\right),\left(Alic{e}_2,T{2}^{\prime }\right)\right)$ (1)

As the three copies of Alice are superposed, the three occurrences are as well. By factoring Alice out, we obtain Equation (2).

$CH=\left(Alice\left(v^{\prime },T{1}^{\prime },T{2}^{\prime }\right)\right)$ (2)

More generally, let αdenote an NP undergoing IM, and let Kand Λ denote occurrences (contexts or sisters that the NP is merged with) of a higher and the original NP copy, respectively. The normalized vector $|\text{CH}\rangle$ of the NP chain state is Equation (3) (Orús et al., 2017: 23).

$|\widehat{CH}\rangle =\frac{1}{\sqrt{2}}\left(|\text{<mover accent="true"> <mi> α </mi> <mo> ^ </mo> </mover>}\rangle \otimes |\hat{K}\rangle +|\hat{\alpha }\rangle \otimes |\hat{\Lambda }\rangle \right)=\frac{1}{\sqrt{2}}|\text{<mover accent="true"> <mi> α </mi> <mo> ^ </mo> </mover>}\rangle \otimes \left(|\hat{K}\rangle +|\hat{\Lambda }\rangle \right)$ (3)

Orús et al. (2017: 23) proposed that a linguistic chain is a superposition of at least two different states, postulating the axiom 8 shown in (6).

(6) Axiom 8 (Hilbert space)

Linguistic chains are normalized sums of vectors from a Hilbert space.

Martin et al. (2019: 30) claimed that syntactic computation “collapses” into interface observables (i.e., a classical linguistic reality) when “syntax acts on some Hilbert space, by way of linear operations.”

Let us focus on the first IM step of the entire CH of Alice $|Alice\rangle$ : CH = (Alice₀, Alice₁, Alice₂). The first subset of a normalized vector of chain CH (Alice) is in the superposed of two occurrence states (i.e., v' and T1'). $|\widehat{\text{CH}\left(Alice\right)}\rangle$ is indicated in Equation 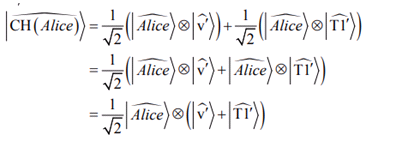(4).

(4)

The scalar $\frac{1}{\sqrt{2}}$ indicates that the resulting vector is set according to the

normalization condition, which dictates that every state’s square sum of probability amplitude must be equal to one. The probability that a copy of Alice is observed at vP edge and that the same copy is observed at the TP1 edge are identical, i.e., 50%, respectively.¹⁶

3. Results

Let us consider how we can differentiate between grammatical (1a) from ungrammatical (1b) linear algebraically. See Appendix B for the matrix calculation for structure building of the grammatical example (1a), the geometry of which is shown in Figure 1, and Appendix C for that of ungrammatical (1b), the geometry of which is shown in Figure 2.

3.1. SVD of Occurrence Matrices

3.1.1. SVD of Occurrence Matrices of Chain Head Alice in (1a)

I focus on the occurrence (i.e., sister) matrices of (potential) chain heads in question: substantive DP (Alice) for (1a) and substantive DP (Alice) and expletive (it) for (1b). For (1a), the relevant occurrences are v', T1', and T2'; (1b), they are v', T1', T2', and T3'. MATLAB returns the singular value decomposition (SVD) result for each occurrence matrix.¹⁷ The SVD results of occurrence matrices of Alice in (1a) are shown in (7).

(7) SVD of occurrence matrix of chain head Alice in grammatical (1a)

a). $\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]$ , and its $\left[\text{U},\text{S},\text{V}\right]=\text{svd}\left(\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}\right)=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$ .

b). $\text{<mi> T </mi> <msup> <mi> 1 </mi> <mo> ′ </mo> </msup>}=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]$ , and its $\left[\text{U},\text{S},\text{V}\right]=\text{svd}\left(\text{<mi> T </mi> <msup> <mi> 1 </mi> <mo> ′ </mo> </msup>}\right)=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]$ .

c). $\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]$ , and its $\left[\text{U},\text{S},\text{V}\right]=\text{svd}\left(\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}\right)=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]$ .

The diagonal matrix S indicates the fundamental characteristics of the matrix. All occurrence matrices show that S is the identity matrix I, as shown in (7), implying that the relevant occurrence does not change. For explanatory purposes, the boldface matrices highlight a point in question.

3.1.2. SVD of Occurrence Matrices of Alice and Expletive It in (1b)

The SVD results of occurrence matrices of potential chain heads Alice and an expletive it in the ungrammatical example (1b) are shown in (8) below.

(8) SVD of occurrence matrix of chain heads Alice and it in ungrammatical (1b)

a). $\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]$ , and its $\left[\text{U},\text{S},\text{V}\right]=\text{svd}\left(\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}\right)=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$ .

b). $\text{<mi> T </mi>}{1}^{\prime }=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]$ , and its $\left[\text{U},\text{S},\text{V}\right]=\text{svd}\left(\text{<mi> T </mi> <msup> <mi> 1 </mi> <mo> ′ </mo> </msup>}\right)=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]$ .

c). $\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]$ , and its $\left[\text{U},\text{S},\text{V}\right]=\text{svd}\left(\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}\right)=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]$ .

d). $\text{<mi> T </mi> <msup> <mi> 3 </mi> <mo> ′ </mo> </msup>}=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]$ , and its $\left[\text{U},\text{S},\text{V}\right]=\text{svd}\left(\text{<mi> T </mi> <msup> <mi> 3 </mi> <mo> ′ </mo> </msup>}\right)=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]$ .

All occurrence matrices show that S is the identity matrix I, implying that the relevant occurrence does not change. Unlike other U’s, the first orthogonal matrix U in the SVD result of T2' occurrence matrix (8c) is a real matrix (indicated by a boldface matrix). Later I will propose that the heterogeneous property of U of occurrence T2’ of the expletive it in (8c) is responsible for a quantum collapse failure.

3.2. Normalized Vectors and Wave Function of Alice Chain in (1a)

Let us consider the normalized vectors of an Alice chain in the grammatical raising example in (1a). Let us recapitulate on the general formula for a normalized vector of a set of chain members. Let $|\text{<mover accent="true"> <mi> K </mi> <mo> ^ </mo> </mover>}\rangle$ and $|\hat{\Lambda }\rangle$ be normalized vectors of two the Alice occurrences. A normalized vector of Alice chain is shown in Equation (5) below.

$|\widehat{\text{CH}\left(Alice\right)}\rangle =\frac{1}{\sqrt{2}}|\widehat{Alice}\rangle \otimes \left(|\text{<mover accent="true"> <mi> K </mi> <mo> ^ </mo> </mover>}\rangle +|\hat{\Lambda }\rangle \right)$ (5)

In Equation (5), $|\widehat{Alice}\rangle$ is factored out of $\left(|\text{<mover accent="true"> <mi> K </mi> <mo> ^ </mo> </mover>}\rangle +|\hat{\Lambda }\rangle \right)$ , which means that the occurrences $|\text{<mover accent="true"> <mi> K </mi> <mo> ^ </mo> </mover>}\rangle$ and $|\hat{\Lambda }\rangle$ share the same chain-member, i.e., $|\widehat{Alice}\rangle$ . Each step of chain formation in the grammatical raising (1a) is expressed as a vector formula in Equation (5). Incidentally, Orús et al. (2017: 25) introduced an ungrammatical vector called a “weird” vector as shown in Equation (6).

$|Weird\rangle =\frac{1}{\sqrt{2}}\left(\text{a}|\hat{\alpha }\rangle \otimes |\hat{K}\rangle +\text{b}|\hat{\beta }\rangle \otimes |\hat{\Lambda }\rangle \right)$ (6)

When $\text{a},\text{b}\ne 0$ , $|\text{<mover accent="true"> <mi> α </mi> <mo> ^ </mo> </mover>}\rangle$ and $|\text{<mover accent="true"> <mi> β </mi> <mo> ^ </mo> </mover>}\rangle$ cannot be factored out, which is called an entangled state. Equation (6) expresses a chain formation step in the ungrammatical (1b), where $|\text{<mover accent="true"> <mi> α </mi> <mo> ^ </mo> </mover>}\rangle =|\widehat{Alice}\rangle$ , and $|\text{<mover accent="true"> <mi> β </mi> <mo> ^ </mo> </mover>}\rangle =|\widehat{it}\rangle$ .¹⁸ I leave the entanglement for future research.

Now, let us consider Figure 1 of (1a) a grammatical geometry. Let us calculate a normalized vector of the first sub-step of the entire Alice chain, which is shown in (9).

(9) Normalized vector of the first sub-step of Alice chain in (1a)

$\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]$ . Since $\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]\cdot \left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$ , the trace of which is 2, normalized vector is $|\widehat{\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}}\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]$ .Similarly, $\text{<mi> T </mi>1'}=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]$ . Since

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\cdot \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$ , the trace of which is 2, the normalized vector is $|\widehat{\text{<mi> T </mi> <msup> <mi> 1 </mi> <mo> ′ </mo> </msup>}}\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]$ . Therefore, $|\widehat{\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}}\rangle +|\widehat{\text{<mi> T </mi> <msup> <mi> 1 </mi> <mo> ′ </mo> </msup>}}\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1+\left(-1\right)& 0\\ 0& i+\left(-i\right)\end{array}\right]=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]$ . Therefore, $|\widehat{\text{CH}\left(Alice\right)}\rangle =\frac{1}{\sqrt{2}}|\widehat{Alice}\rangle \otimes 0=0$ .

In the grammatical geometry (Figure 1), the normalized vector of the first sub-step occurrence of the Alice chain is zero. Next, let us calculate a normalized vector of the second sub-step occurrence of the entire Alice chain in Figure 1, which is shown in (10).

(10) Normalized vector of the second sub-step occurrence of Alice chain in (1a)

$\text{<mi> T </mi>1'}=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]$ . Since $\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\cdot \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$ , the trace of which is 2, the normalized vector is $|\widehat{\text{<mi> T </mi> <msup> <mi> 1 </mi> <mo> ′ </mo> </msup>}}\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]$ .Similarly, $\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]$ . Since $\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\cdot \left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$ , the trace of which is 2, normalized vector is $|\widehat{\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}}\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]$ . Therefore, $|\widehat{\text{<mi> T </mi> <msup> <mi> 1 </mi> <mo> ′ </mo> </msup>}}\rangle +|\widehat{\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}}\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{cc}-2& 0\\ 0& 0\end{array}\right]=\left[\begin{array}{cc}-\sqrt{2}& 0\\ 0& 0\end{array}\right]$ . Now, let us calculate a normalized vector of Alice chain. Since $Alice=\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]$ , and $\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\cdot \left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]$ , the trace of which is 2, a normalized vector is $|\widehat{Alice}\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]$ . Therefore,

$\begin{array}{c}|\widehat{\text{CH}\left(Alice\right)}\rangle =\frac{1}{\sqrt{2}}|\widehat{Alice}\rangle \otimes \left(|\widehat{\text{<mi> T </mi> <msup> <mi> 1 </mi> <mo> ′ </mo> </msup>}}\rangle +|\widehat{\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}}\rangle \right)=\frac{1}{2}\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\otimes \left[\begin{array}{cc}-\sqrt{2}& 0\\ 0& 0\end{array}\right]\\ =\frac{1}{2}\left[\begin{array}{cc}1\cdot \left[\begin{array}{cc}-\sqrt{2}& 0\\ 0& 0\end{array}\right]& 0\cdot \left[\begin{array}{cc}-\sqrt{2}& 0\\ 0& 0\end{array}\right]\\ 0\cdot \left[\begin{array}{cc}-\sqrt{2}& 0\\ 0& 0\end{array}\right]& -i\cdot \left[\begin{array}{cc}-\sqrt{2}& 0\\ 0& 0\end{array}\right]\end{array}\right]\\ =\frac{1}{2}\left[\begin{array}{cccc}-\sqrt{2}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \sqrt{2}i& 0\\ 0& 0& 0& 0\end{array}\right]=\left[\begin{array}{cccc}-\frac{\sqrt{2}}{2}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \frac{\sqrt{2}}{2}i& 0\\ 0& 0& 0& 0\end{array}\right]\end{array}$

Using MATLAB to apply SVD, we obtain

$\begin{array}{l}\left[\text{U},\text{S},\text{V}\right]=\text{svd}\left(\widehat{\text{CH}\left(Alice\right)}\right)\\ =\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& -i& 0& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{cccc}0.7071& 0& 0& 0\\ 0& 0.7071& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{cccc}-1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& -1& 0& 0\\ 0& 0& 0& 1\end{array}\right]\end{array}$

Significantly, the scaling matrix S (indicated by a boldface matrix) in the SVD matrix is not I, and its (1, 1) (i.e., row 1, column 1) and (2, 2) positions have values that are smaller than one, but not zero. This means that the normalized vector of the second sub-step of the Alice chain tends to diminish. The grammatical (1a) shows a wave function ψof Alice chain vector consisting of a 4 by 4 complex matrix in Equation (7).

$\psi =\left[\begin{array}{cccc}-\frac{\sqrt{2}}{2}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \frac{\sqrt{2}}{2}i& 0\\ 0& 0& 0& 0\end{array}\right]$ (7)

Calculating its squared length ${\Vert \psi \Vert }^2$ , we obtain a probability as shown in Equation (8) regarding where the plural copies of Alice are observed in Figure 1.

${\psi }^2={\psi }^{†}\psi =\left[\begin{array}{cccc}-\frac{\sqrt{2}}{2}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& -\frac{\sqrt{2}}{2}i& 0\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{cccc}-\frac{\sqrt{2}}{2}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \frac{\sqrt{2}}{2}i& 0\\ 0& 0& 0& 0\end{array}\right]=\left[\begin{array}{cccc}\frac{1}{2}& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& \frac{1}{2}& 0\\ 0& 0& 0& 0\end{array}\right]$ (8)

The probability matrix in Equation (8) contains $\frac{1}{2}$ at (1, 1) and (3, 3) positions. There is a 50% probability of Alice being in the TP1 or TP2 edge; in other words, the same NP simultaneously exists in two different positions. The superposed states collapse into one in SM and CI. In Figure 1, the superposed state collapses into Alice at TP2 edge. If a collapse happens at the TP1 edge, SM externalizes (11).

(11) It seems for Alice to like Bob.

In (11), when Alice has reached at TP1 edge, a distinct derivation is realized, where a preposition for is inserted as a last resort to eliminate Alice’s case, i.e., a probe uF [ACC] (accusative feature) in for eliminates a goal uF [acc] of Alice.¹⁹

4. Discussion

4.1. A Mathematical Structure of Grammatical Chain Formation

A normalized vector of a grammatical chain of Alice in (1a) has three significant properties, as shown in (12).

(12) a). The SVD-diagonal matrix (i.e., the middle matrix Sin [U, S, V]) of occurrence matrices of Alice, as shown in each SVD matrix in (7), is the identity matrix I.

b). The value of the first chain sub-step is zero, as shown in the last line of (9).

c). The S value of the second sub-step is 0.7071, as shown in the last line of (10).

The basic property of occurrence matrices, according to property (12a), indicates that they provide a stable mode. Regarding property (12b), I argue that the zero value of the first sub-step of CH corresponds to the fact that the SM does not externalize the intermediate chain-member copies, i.e., Alice₀ and Alice₁. This is notable because it is a linear-algebraic proof that intermediate copies are not externalized. Property (12c) indicates that chain-member copies in the final IM step are in a decaying mode given that the infinite power of 0.7071 approaches zero but never reaches zero.

Let’s use geometry to express these properties and tendencies. Regarding (12a), let us assume that the geometrical form of I is a unit circle, i.e., a basic form. The geometrical occurrence forms (syntactic contexts) remain in the same unit circle. As to (12c), the value 0.7071 shows that the geometrical form of Alice chain copies approaches zero-dimensional point infinitesimally toward the chain head.²⁰ Figure 4 (to be modified) shows the geometrical image schematically. The chain geometry teaches us that the chain copies undergo a dimensional drop from 2 to 0, whereas the occurrences (syntactic contexts) are stable, i.e., they remain 2 dimensions. A direction of dimension drop equals a direction of chain realization toward the highest chain member, a point at which SM externalizes an Alice copy, just as a direction of potential drop equals a direction in which a current flows (Strang, 2016: 458).

Medeiros (2012: 244-245) calculated the growth factor of the spine, i.e., the head-complement structure, as shown in (13), where PSR stands for phrase structure rule, a characteristic polynomial is used to find eigenvalues, which describes the fundamental property of the relevant matrix, the black circle corresponds to a head, and the blank triangle indicates a phrase.

Figure 4. Geometrical image of the second sub-step of chain formation (to be modified).

(13) The Spine (adapted from Medeiros (2012: 244))

PSR: 1 → 0 1

Matrix: $\left[\begin{array}{cc}1& 0\end{array}\right]$

Characteristic polynomial: x– 1

Growth factor: 1

Tree:

Given that Medeiros’ spines correspond to chain occurrences, i.e., v’, T1’, and T2’ in Figure 1, I believe it is significant that the spine’s growth factor is 1 (i.e., nothing changes; equals the identity matrix I), which corresponds to our finding that the basic property of occurrence matrices of the grammatical chain formation in (1a) and Figure 1 is that they are stable, as shown in (13), which is geometrically described as the check unit circles in Figure 4.

Regarding the growth factor of the sentential geometry using IMs, I adopt Medeiros’ result that the sentential-structure-building growth factor is φ ~ 1.618, as shown in (14).²¹

(14) X-bar (adapted from Medeiros (2012: 245))

PSR: 2 → 2 1, 1 → 0 2

Matrix: $\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]$

Characteristic polynomial: x² – x – 1

Growth factor: φ ~ 1.618

Tree:

The growth factor φ ~ 1.618 is a positive larger root of the x² − x − 1 = 0 characteristic polynomial. The matrix in (14) is the Fibonacci (F) matrix, which describes F sequence. Medeiros (2012) and Medeiros and Piattelli-Palmarini (2018) persuasively argued that the golden rule determines the growth factor of geometry-creation in C_HL. As indicated in Carnie and Medeiros (2005: 52), Medeiros (2008: 161), and Medeiros (2012: 220), it is significant that C_HL creates a geometry whose basic property is governed by the golden rule. The diagram in Figure 5 is adapted from Medeiros (2012: 220), which indicates an idealized linguistic tree, where its edge and complement are maximized, and how F numbers emerge in the tree.

(15) F emerging in Figure 5

a). XP = {1, 1, 2, 3, 5, 8, …} = Fib(n)

b). X’ = {0, 1, 1, 2, 3, 5, …} = Fib(n − 1)

c). X = {0, 0, 1, 1, 2, 3, …} = Fib(n − 2)

The complement XP and the edge XP are maximized in Figure 5. Count the number of XP, X’, and X⁰ for each derivational line, F sequence defined by the linear recurrence equation F_n = F_n–1 + F_n–2, where F₁ = F₂ = 1 and F₀ = 0, appears²², i.e., F = {0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …}, as indicated in (15).

A new finding of this paper is that the chain copy members, Alice copies here, tend to diminish, approaching zero, but never reach zero, as shown by S in the last line of (10), which is geometrically described as diminishing circles toward TP2 edge. Here it is tempting to propose a hypothesis that the emergence of diminishing value 0.7071 corresponds to the little φ ~ −0.618, which is the other solution (eigenvalue) of x² − x − 1 = 0, i.e., infinite power of both numbers approaches zero, but never reaches zero. If this logic is true, the hypothesis that chain-member copies diminish is probable. Following Medeiros (2012) and Medeiros and Piattelli-Palmarini (2018), assume that the basic property of C_HL-geometry building is the golden rule, which determines the growth factor of F sequence. Strictly speaking, the growth factor of F numbers consists of both the greater φ ~ 1.618 and little φ ~ −0.618, where the infinite power makes the former grow exponentially, and the latter becomes infinitesimally small; approaching zero, but never reaching zero. This is the reason why the little φ is

Figure 5. A maximized X’-tree.

often ignored. Therefore, it is reasonable that the chain-formation geometry contains both exponential boost and infinitesimal shrinkage. Thus, we modify Figures 4 to Figure 6, which is more accurate. In Figure 6, the identity matrix I is expressed by the constant unit circles, the greater φ ~ 1.618 by the enlarging circles, and the little φ ~ −0.618 by the diminishing circles.

The fundamental MP assumptions and network theory support Figure 6. A DP (NP) with a set of uF externally merges at a position where it is assigned a $\text{θ}$ role. The driving force of IM is uF elimination, which means that the uF number decreases as the DP undergoes successive IM bottom-up. The currents (i.e., edge information) flow in the direction of a potential (i.e., node information) drop, according to network theory (Strang, 2016: 458). A set of chain-head DPs reduces uF numbers, corresponding to diminishing circles in Figure 6. The MP dictates that a sentential-structure building proceeds bottom-up, accumulating information, which theoretically corresponds to the exponential growth factor of a positive golden ratio. However, C_HL uses IM edges to create loops and the loops lead to equilibrium, avoiding a computational explosion (Arikawa, 2019). A spine ( $\bar{X}$ ) is formed by externally merging a head X and its complement YP, which is transferred to the interfaces as soon as possible. A higher probe targets X and its edges but not the spine $\bar{X}$ . A spine $\bar{X}$ is invisible to C_HL and does not affect the computational result, which is due to the spine’s extreme symmetry, as expressed by the identity matrix (i.e., unit circle).

4.2. A Mathematical Structure of Ungrammatical Chain Formation

Now consider a CH (Alice) in an ungrammatical (super-raising; (1b)) geometry, as shown in Figure 2. The basic property of ungrammatical (1b) occurrence matrices is the same as that of grammatical (1a), as indicated by the diagonal matrices S in (8) and those in (7), respectively. Consequently, the matrix calculation yields the same value of normalized vector for ungrammatical super-raising and grammatical raising geometries. Therefore, this analysis faces a problem (16).

Figure 6. Geometrical image of the second sub-step of chain formation (modified).

(16) A problem

We cannot distinguish the grammatical chain from the ungrammatical one in terms of values of normalized vectors. Is there a way to algebraically differentiate between the two types of CH?

Two possible algebraic ways to differentiate grammaticality are shown in (17).

(17) Two possible solutions

a). Use the basic property (i.e., I) of occurrence matrices.

b). Use the left orthogonal matrix U.

Consider the diagonal S (i.e., Σ) of SVD of these occurrences for the initial solution (17a). As shown in (8), the occurrence matrices of the ungrammatical chain is I. SVD shows that σ₁ (upper-left corner) of diagonal matrix S is equal to one. Thus, the maximum growth factor equals one (Strang, 2016: 382), indicating that the occurrence is stable.²³ The identity property of occurrence matrices causes all chain-member copies of CH to be identical. Let us adopt the fundamental concept of context-sensitivity (Bošković, 2013, 2014) and propose the context-sensitivity hypothesis as shown in (18).

(18) The context-sensitivity hypothesis (original version, ibid.)

If the syntactic contexts of X vary, so does its status.

Suppose that the inverse of the conditional proposition in (18) is true, as shown in (19).

(19) The inverse of context-sensitivity hypothesis

If the syntactic contexts of X are identical, X’s status is identical.

As indicated by all S’s (i.e., the growth factor matrices) in (8), the syntactic contexts are the same, implying that their sisters are identical. However, the DP Alice and the expletive it are not identical, which contradicts (19). Alternatively, in (1b), the geometry of which is shown in Figure 2, the absolute CH uniformity requires Alice = it, which is a syntactic, semantic, and phonetic contradiction. Thus, the potential CH in Figure 2 contains a linear-algebraic contradiction, leading to ungrammaticality.²⁴ However, in Figure 1, a geometry of (1a), the three CH-heads are identical, i.e., Alice₀ = Alice₁ = Alice₂; and the sentence is grammatical, conforming to (19). The members of the relevant chain are completely uniform.

According to MP, as stated in section 1, (1b) is ungrammatical because Alice skipped over a potential-intermediate landing site, the TP2 edge, on its way to the final landing site, the TP3 edge, violating MC. However, given the Greed-LR principle in MP, the solution must be elaborated. Why is the Greed-LR principle not invoked in such a way that Alice is forced to skip the potential landing site if the expletive it is frozen at the TP2 edge and does not move out of the way? Why does MC take precedence over the Greed-LR principle? Another way to account for (1b) ungrammaticality using MS is to use a broader concept of chain that includes a potential landing site, i.e., potential CH = {TP3-edge, TP2-edge, TP1-edge, vP-edge}. The significant finding is that the occurrence (syntactic context) matrix calculation (i.e., the growth factor matrix S in SVD in (8)) reveals that the identity matrix I (see also (13)) describes the basic property of these occurrences (Alice-occurrence nodes = v', T1', T3' and it-occurrence node = T2' in Figure 2). If these occurrences (syntactic contexts) are identical, then their sisters must also be identical as well (19). It forces us to conclude that Alice = it, despite breaking every rule of syntax, semantics, and phonetics. Example (1b) is ungrammatical because the sentential geometry matrix calculation forces Alice to be equated to it, resulting in crashes at CI and SM.

Consider how the left orthogonal matrices U can be used in the second solution (17b). As shown in (8c), one distinguishing feature of the occurrence matrix T2' of expletive it is that its U is a real matrix, unlike other U’s, which are complex. Consider the following fact, on which SVD is entirely dependent (Strang, 2016: 365).

(20) Grayscale fact

Grayscales of nearby pixels are generally similar.

An image is a large matrix (ibid.). Similarly, a sentential structure is a large matrix. The entry a_ij describes the grayscale of each pixel in the image. It is difficult to compress different grayscales. A grammatical set of chain-member contexts constitute grayscales that can be compressed. However, a super-raising structure has a different context, i.e., SVD results with a real-matrix U. The different context causes the compression impossible, resulting in the ungrammatical status of (1b). An SVD factorizes a matrix A as $\text{A}=\text{U}\Sigma {\text{V}}^{\text{<mi> T </mi>}}$ , which has the geometrical meaning of which is (rotation) times (stretching) times (rotation). A real matrix represents stretching, whereas a complex matrix represents a rotation and stretching. A super-raising structure, as shown in (8c), contains complex-U syntactic contexts for DP Alice, and real-U context for the expletive it. An informal formula for a super-raising quantum state is shown in Equation (9), where a tensor-product symbol $\otimes$ represents IM and dot product $\cdot$ represents EM.

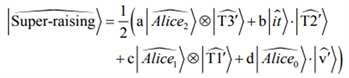(9)

In Equation (9), unlike other occurrences (i.e., syntactic contexts) with complex-U’s, the occurrence $|\widehat{\text{<mi> T </mi> <msup> <mi> 2 </mi> <mo> ′ </mo> </msup>}}\rangle$ of expletive $|\widehat{it}\rangle$ contains a real-U. As mentioned in Subsection 3.1.2, the heterogeneous property of U of occurrence T2’ of the expletive it in (8c) may result in quantum collapse failure at CI and SM, i.e., Alice cannot be interpreted or externalized at a single position when a speaker makes an observation, i.e., she is aware of grammaticality.

5. Conclusion

An insight about MS is that its conditions are consistent with QM, which provides more general tools to handle and investigate information in general. The MP C_HL study can be integrated with complex dynamics using MS and linear algebra. The Merge has a property of simple iterations, resulting in a complex butterfly effect with discrete infinity. I list the findings of this research.

(21) Chain properties are calculable linear algebraically, and it can be used as a key to solving hard problems of MP and MS: Why does internal merge create A-chains in this way, and not in other logically possible ways? What does it mean for such occurrences (i.e., syntactic contexts such as v', T1', T2' in Figure 1) to be a way to distribute an item like Alice over a phrase marker? The MP and MS can collaborate to tackle the hard problem.

(22) LetCH = (X₃, X₂, X₁) a grammatical chain, where X₁ is an EM-copy of X, and X₂ and X₃ are IM-copies of X.

(a) The normalized vector value of the first sub-step of a chain is equal to zero in the scaling matrix S (the last line of (9)), showing that the SM does not externalize X₂, i.e., the kinetic energy is zero.

(b) The normalized-vector S value of the second sub-step is 0.7071 (the last line in (10)), indicating that the chain-member copies (X₃, X₂, X₁) tend to diminish in the direction from X₁ to X₃. 2D area approaches zero-dimensional point infinitesimally, which corresponds to a potential drop in graph theory, causing information to flow toward the drop. SM externalizes the highest chain-member copy X₃, a zero-dimensional point where a computation converges.

(c) The S of the occurrences (sister node of chain copies; the syntactic context of chain members) is the identity matrix I, indicating that the occurrences are in steady mode.

(23) The calculation leads to the dynamics of chain-forming geometry in C_HL (Figure 6). A chain-forming geometry contains three areas with distinct growth factors: (a) occurrences (spine) in a steady mode, (b) the entire structure building in a developing mode at an exponential rate (i.e., greater φ ~ 1.618), and (c) the chain-member copies in a decaying mode (i.e., little φ ~ −0.618 or σ₁ = 0.7071).

(24) Two possible ways to distinguish linear-algebraically grammatical from ungrammatical raising are:

(a) MATLAB returns the SVD result of occurrence (i.e., syntactic context) of potential-chain members, where every scaling matrix (S = Σ) is I. The inverse of context-sensitivity hypothesis demands that the members of a potential chain must be identical. In an ungrammatical raising (super-raising) geometry, one of the potential-chain members is an expletive, forcing “Alice = it,” which is a contradiction.

(b) Unlike the occurrence matrices of the chain member Alice, where the rotational matrices U’s are all complex, the SVD result is peculiar for the occurrence matrix of the expletive it, where the rotational matrix U is real. The heterogeneous property of U of occurrence T2' is responsible for failures of compression and quantum collapse, i.e., Alice copy cannot be externalized at one position in ungrammatical super-raising when a speaker makes grammaticality observation.

A practical implication based on the current research results is that this paper may enhance collaboration among the MP linguists, mathematicians, and physicists, which was initiated by Orús et al. (2017) and Martin et al. (2019), as well as a scientific investigation into C_HL.

Regarding the following studies, my perusal is necessary for Orús et al. (2017) and Martin et al. (2019) to continue the MS project in detail. My MS learning must parallel with the MP investigation, which is the linguistic foundation of MS. Simultaneously, I need to continue studying linear algebra by reading a textbook, such as Strang (2016), because linear algebra is a fundamental mathematical tool used in MS.

Acknowledgements

I want to thank an anonymous reviewer for taking the time and effort necessary to review the manuscript. I sincerely appreciate all the valuable comments and suggestions that have helped me improve the manuscript’s quality. This work was supported by JSPS KAKENHI Grant Number JP21K00491 and the Momoyama Gakuin (St. Andrew’s) University Fund for Research Support. The author wants to thank Enago (http://www.enago.jp) for the English language review.

Appendices

A). MS toolkit

Orús et al. (2017) and Martin et al. (2019) adopted the standard Dirac (bra-ket) notation as shown in (1) below to define a scalar product.

$\langle \text{A}|\text{B}\rangle =\text{<mi> T </mi>r}\left({\text{A}}^{\text{†}}\text{B}\right)$ (1)

In (1), the ket $|\text{B}\rangle$ is a system state, the bra $\langle \text{A}|$ is a scalar, tr is the matrix trace, i.e., the sum of its diagonal entries, which equals to the sum of eigenvalues, and ${\text{A}}^{†}$ (read as “A dagger”) is the conjugate transpose of a complex matrix A.²⁵

Pierce (2021) provides a concise statement regarding the reason why we use bra-ket notation. Namely, “[t]he bra-ket notation ⟨bra|ket⟩ is a way of writing special vectors used in QM. A ket is a quantum state, the values of which are complex numbers, and it can have any number of dimensions, including infinite dimensions. The bra is similar, but the values are in a row, and each element is the complex conjugate of the ket’s elements. We can ‘map’ some real-world case (usually one with probabilities) onto a well-defined mathematical basis. This then gives us the power to use all the math tools to study it (ibid).” The norm N (also called size, length, modulus, magnitude, or absolute value) of a vector $|\text{z}\rangle$ is shown in (2).

$\text{N}=\left|\sqrt{\langle \text{z}|\text{z}\rangle }\right|=\left|\sqrt{\text{<mi> T </mi>r}\left({\text{z}}^{\text{†}}\text{z}\right)}\right|$ (2)

When obtaining inner products of complex vectors, we must use Hermitian matrices to avoid contradictions.²⁶ A vector zwith norm N = 1 is called a normalized vector, which corresponds to $\text{<mover accent="true"> <mi> z </mi> <mo> ^ </mo> </mover>}$ (read “z-hat”), as indicated in (3).

$\text{N}\left(|\text{<mover accent="true"> <mi> z </mi> <mo> ^ </mo> </mover>}\rangle \right)=\frac{\text{1}}{\sqrt{\langle \text{z}|\text{z}\rangle }}|\text{z}\rangle =\frac{\left|\text{z}\right|}{\left|\text{z}\right|}=1$ (3)

For example, $\widehat{\text{NP}}$ of $\text{NP}=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$ is shown in (4), where $\langle \text{NP}|\text{NP}\rangle =2$ .

$|\widehat{\text{NP}}\rangle =\frac{1}{\sqrt{\langle \text{NP}|\text{NP}\rangle }}|\text{NP}\rangle =\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]$ (4)

See Orús et al. (2017: 19) and Martin et al. (2019) for relevant definitions.

B). Structure building of grammatical (1a)

In Orús et al. (2017: 10), Axiom 3 (multiplication) states that 1^st MERGE (M) is matrix multiplication, and Axiom 4 (tensor product) elsewhere M [non-first MERGE] is matrix tensor product. The former corresponds to EM, and the latter to IM.²⁷ The matrix calculation of the entire structure building of grammatical (1a) is shown in (1) below.

(1) Matrix calculation for(1a) = Figure 1

1) V1 (like) EMs with NP (Bob).

$\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]=\text{VP}1$

2) v EMs with VP1.

$\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\times \left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}$

3) NP (Alice) EMs with v'.

$\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\text{vP}$

4) T1 (to) EMs with vP.

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]=\text{<mi> T </mi>}{1}^{\prime }$

5) NP (Alice) IMs with T1'.

$\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\otimes \left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]=\left[\begin{array}{cc}1\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]& 0\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\\ 0\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]& -i\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\end{array}\right]=\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1\end{array}\right]=\text{<mi> T </mi>P}1$

6) SVD compresses TP1 matrix to TP1 = UΣV^T, where diagonal matrix Σ (scaling factor; singular value) indicates how axes stretch, and orthogonal (unitary) matrices U and V^T indicate how vectors rotate (U^TU = UU^T = I, V^TV = VV^T = I). MATLAB returns the following result of SVD for TP1.

$\text{<mi> T </mi>P}1=\text{U}\Sigma {\text{V}}^{\text{<mi> T </mi>}}=\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1\end{array}\right]$

Singular value Σ is I. Therefore, 4-by-4-TP1 matrix is compressed into 2-by-2 I.

7) V2 (seem) EMs with TP1.

$\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\text{VP}2$

8) V2 (seem) IMs with T2 (s; 3, sg).

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\otimes \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}-1\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\\ 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& -i\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\end{array}\right]=\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]=\text{<mi> T </mi>}2$

9) SVD compresses T2 matrix to T2 = UΣV^T. MATLAB returns the following SVD.

$\text{<mi> T </mi>}2=U\Sigma V^{\text{<mi> T </mi>}}=\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]$

SV matrix Σ is I. Therefore, 4-by-4-T2 matrix is compressed into 2-by-2 I.

10) T2 (seem) EMs with VP2.

$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\times \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\text{<mi> T </mi>}{2}^{\prime }$

11) NP (Alice) IMs with T2'.

$\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\otimes \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}1\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\\ 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& -i\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\end{array}\right]=\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]=\text{<mi> T </mi>P2}$

12) SVD compresses TP2 matrix to UΣV^T. MATLAB returns the following SVD.

$\text{<mi> T </mi>P2}=\text{U}\Sigma {\text{V}}^{\text{<mi> T </mi>}}=\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1\end{array}\right]$

SV matrix Σ is I. Therefore, 2-by-2-TP2 matrix is compressed into 2-by-2 I.

13) C EMs with TP2.

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]=\text{CP}$

C). Structure building of ungrammatical (1b)

A matrix calculation for the entire structure building of ungrammatical (1b) = Figure 2 is shown in (1) below.

(1) Matrix calculation for (1b) = Figure 2

1) V1 (like) EMs with NP (Bob).

$\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]=\text{VP}1$

2) v EMs with VP1.

$\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\times \left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\text{<msup> <mi> v </mi> <mo> ′ </mo> </msup>}$

3) NP (Alice) EMs with v'.

$\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\text{vP}$

4) T1 (to) EMs with vP.

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]=\text{<mi> T </mi>}{1}^{\prime }$

5) NP (Alice) IMs with T1'.

$\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\otimes \left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]=\left[\begin{array}{cc}1\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]& 0\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\\ 0\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]& -i\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\end{array}\right]=\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1\end{array}\right]=\text{<mi> T </mi>P}1$

6) MATLAB returns the following result of SVD for TP1.

$\text{<mi> T </mi>P}1=\text{U}\Sigma {\text{V}}^{\text{<mi> T </mi>}}=\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill -1\end{array}\right]$

Singular value Σ is I. Therefore, 4-by-4-TP1 matrix is compressed into 2-by-2 I.

7) A (certain) EMs with TP1.

$\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\text{AP}$

8) V2 (auxiliary verb be) EMs with AP.

$\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]=\text{VP}2$

9) V2 (auxiliary verb be) IMs with T2 (3, sg).

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\otimes \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}-1\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\\ 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& -i\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\end{array}\right]=\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]=\text{<mi> T </mi>}2$

10) SVD compresses T2 matrix to UΣV^T. MATLAB returns the following SVD.

$\text{<mi> T </mi>}2={\text{UΣV}}^{\text{<mi> T </mi>}}=\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]$

SV matrix Σ is I. Therefore, the 4-by-4-T2 matrix is compressed into 2-by-2 I.

11) T2 (is) EMs with VP2.

$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\times \left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]=\text{<mi> T </mi>}{2}^{\prime }$

12) Expletive (it) EMs with T2'.

$\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\times \left[\begin{array}{cc}-1& 0\\ 0& -1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\text{<mi> T </mi>P}2$

13) C1 EMs with TP2.

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\times \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\text{CP}1$

14) V3 (seem) EMs with CP1.

$\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\text{VP}3$

15) V3 (seem) IMs with T3 (s; 3, sg).

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\otimes \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}-1\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\\ 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& -i\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\end{array}\right]=\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]=\text{<mi> T </mi>}3$

16) SVD compresses T3 matrix to UΣV^T. MATLAB returns the following SVD.

$\text{<mi> T </mi>}2=\text{U}\Sigma {\text{V}}^{\text{<mi> T </mi>}}=\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{rrrr}\hfill 1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]$

SV matrix Σ is I. Therefore, the 4-by-4-T3 matrix is compressed into 2-by-2 I.

17) T3 EMs with VP3.

$\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\times \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\text{<mi> T </mi>}{3}^{\prime }$

18) NP (Alice) IMs with T3'.

$\left[\begin{array}{cc}1& 0\\ 0& -i\end{array}\right]\otimes \left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]=\left[\begin{array}{cc}1\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\\ 0\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]& -i\left[\begin{array}{cc}-1& 0\\ 0& i\end{array}\right]\end{array}\right]=\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]=\text{<mi> T </mi>P}3$

19) SVD compresses TP3 matrix to UΣV^T. MATLAB returns the following SVD.

$\text{<mi> T </mi>P}2=\text{U}\Sigma {\text{V}}^{\text{<mi> T </mi>}}=\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill i& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill i& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]\left[\begin{array}{cc}\begin{array}{cc}1& 0\\ 0& 1\end{array}& \begin{array}{cc}0& 0\\ 0& 0\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{cc}1& 0\\ 0& 1\end{array}\end{array}\right]\left[\begin{array}{rrrr}\hfill -1& \hfill 0& \hfill 0& \hfill 0\\ \hfill 0& \hfill -1& \hfill 0& \hfill 0\\ \hfill 0& \hfill 0& \hfill -1& \hfill 0\\ \hfill 0& \hfill 0& \hfill 0& \hfill 1\end{array}\right]$

SV matrix Σ is I. Therefore, the 2-by-2-TP3 matrix is compressed into 2-by-2 I.

20) C2 EMs with TP3.

$\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]\times \left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& -i\end{array}\right]=\text{CP}2$

NOTES

¹There are two PIC definitions, where domain of H is a complement of H, and strong phases are v*P (v* = unergative v) and CP.

(i) a. PIC-I: In phase α with head H, the domain of H is not accessible to operations outside α, only H and its edge are accessible to such operations (Chomsky, 2000: 108).

b. PIC-II: The domain of H [a strong phase head] is not accessible to operations at ZP [a next higher strong phase]; only H and its edge are accessible to such operations (Chomsky, 2001: 13-14). PIC-II loosened PIC-I, i.e., PIC-II allows procrastination. In PIC-I, once an immediately lower strong phase HP is formed, any operation from outside is restricted to H and HP edge. PIC-II invokes such a restriction only after the immediately higher strong phase is formed. See Arikawa (2020) for a graph-theoretical analysis proposing that weak phases (VP, TP) are catalysts for strong phrases (vP, CP).

² Chomsky (1986b: 18) named (i) “super-raising”, where IP = TP, and t = trace.

(i) * John seems [_CP that it is certain [_IP t to win]].

Chomsky (1986b) used the empty category principle (ECP; a rule that governs where a silent element appears in a sentence) to explain the ungrammatical status of (i), i.e., the John trace is not properly governed, i.e., it is neither close to V nor licensed by a local binder. MP has discarded ECP.

³Even the pronouns she and he have uF gender as evidenced by transgender facts.

⁴An alternative is to assume a probe uF [NOM], which eliminates [nom] in DP under matching, which is simpler than the “side-effect” analysis of case elimination.

⁵The MP uses MC to answer this question: it is costless to externalize just one copy. But why one?

⁶See Smolensky (1990) for reinterpretation of the optimality theory regarding phonology and morphology using quantum mechanical tools.

⁷ Orús et al. (2017) and Martin et al. (2019) did not discuss ungrammatical (1b).

⁸ Martin et al. (2019: 30) stated that they were not the first to bring QM toolbox into the discussion of language, e.g., to make symbolic AI systems more solid and flexible, Smolensky (1990) used QM tools as tensor product and superposition and applied them to phonological phenomena in the connectionist theory.

⁹It is important to note that any orthogonal quantities do the same work; MS chooses typical orthogonal entities: one on the real axis and i on the imaginary axis that are orthogonal on the complex plane.

¹⁰ Orús et al. (2017: 13) states that Axiom 6 is based on insights of Guimarães (2000).

¹¹Z is the most elegant because it is very symmetrical. Both twins ±Z have the same characteristic polynomial x² −1, the eigenvalues are real (1 and −1), and the trace (i.e., the sum of the entries along the main diagonal (Strang, 2016: 294) is zero. Z is more symmetrical than the identity matrix I, the characteristic polynomials of which are different between I and −I.

¹²The graph was conceptualized by physicist Michael Jarret (Orús et al., 2017: 14).

¹³ Orús et al. (2017: 28) states that “the combination of Axiom 1 (Chomsky matrices), Axiom 3 (matrix multiplication as 1st M), and Axiom 12 (reflection symmetry) yields a unique set of 32 matrices with the structure of a non-abelian group.” The 32 matrices form an enlarged “periodic table” (ibid.) that is used to investigate an entire sentential structure. For example, NumP (number phrase) = $\pm \text{X}=\pm \left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$ , IP (TP) = $\pm i\text{X}=\pm \left[\begin{array}{cc}0& i\\ i& 0\end{array}\right]$ , and DegP (degree phrase) = $\pm i\text{Y}=\pm i\left[\begin{array}{cc}0& -i\\ i& 0\end{array}\right]=\pm \left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]$ (ibid., 28, 40).

¹⁴ Martin et al. (2019: 39). Uriagereka (2019: approximately at 34:00) mentions that lexical categories such as N and V are formed by diagonal G₈ and the twins (16 matrices) that are commutative, whereas functional categories such as T and C by non-diagonal 16 matrices that are non-commutative. In matrix multiplication, non-commutativity is more general than commutativity that is based on special diagonal matrices. A contrast between (i) and (ii) is interesting in this regard.

(i) a. a cat that is a mother (A that is B)

b. a mother that is a cat (B that is A)

(ii) a. the cat’s mother (A’s B)

b. the mother’s cat (B’s A)

Examples in (i) with a copula be obey the commutative law, i.e., (ia) = (ib), and those in (ii) with a genitive ’s disobey it, i.e., (iia) ≠ (iib). Expressions with lexical category V (be) obey the commutative law, whereas those with functional category (genitive; GEN) are non-commutative. The former is similar to multiplication of diagonal matrices, whereas the latter multiplication of non-diagonal matrices. As Strang (2016: 439) states, “with [Hermitian] complex vectors, u^Hv is different from v^Hu. The order of the vectors is now important. In fact ${\text{v}}^{\text{H}}\text{u}={\text{<mover accent="true"> <mi> v </mi> <mo> ¯ </mo> </mover>}}_1{\text{u}}_1+\cdots +{\text{<mover accent="true"> <mi> v </mi> <mo> ¯ </mo> </mover>}}_{\text{n}}{\text{u}}_{\text{n}}$ is the complex conjugate of u^Hv.” A matrix S is Hermitian if S = S^H, i.e., ${\text{s}}_{ij}=\overline{{\text{s}}_{\text{ji}}}$ , where s is an entry in S (ibid. 440). A Hermitian matrix is non-commutative, whereas an anti-Hermitian matrix is commutative. Translating (i) and (ii) into linear algebra, a lexical element such as V is anti-Hermitian, whereas functional element such as D is Hermitian. Orús et al. (2017: 34) presented a table indicating the first set of unit matrices, in which those with “context label” (det(U_c))²/N = +1 are Hermitian, and those with −1 are anti-Hermitian. Although a rigorous proof is beyond the current paper’s ability, a syntactic contrast between (i) and (ii) is translated into an algebraic difference.

¹⁵We need eigenvalues, because they inform us about the essential properties of matrices, such as symmetry (e.g., how a system is unchanged and changed) and commutativity (e.g., how a system is affected by permutation). For example, λ = 2 means that a special vector x (eigenvector) tends to stretch (grow) by a factor of 2 when A acts on x infinitely many times, $\lambda =\frac{1}{2}$ means that x tends to shrink by a factor $\frac{1}{2}$ , approaching zero (decaying mode), λ = −1 means that x tends to reverse the sign, λ = 1 means that x tends to remain as it is, and λ = 0 indicates that a system is singular, i.e., not solvable. Significantly, λ = isuggests that x involves rotation. See Strang (2016: 288-289) for a plain introduction of eigenvalue and eigenvector.

¹⁶The materialization (externalization; pronunciation) of Alice in the root clause is obligatory in (1a) and Figure 1. One might wonder how this system delivers the obligatoriness of materialization of the highest copy and (b) what it contributes with respect to other analyses. As for externalization, I follow Orús et al. (2017: 24), which states that “once a superposed quantum is observed in the appropriate basis, it “collapses” in one of the superposed options as a result of the measurement, which also dictates the measurement outcome,” which is their Axiom 9 (interface).

(i) Axiom 9 (interface): when a chain $|\psi \rangle$ is sent to an interface, its vector gets projected in one of the elements $|\varphi \rangle$ being specified according to the probability ${\left|\langle \varphi |\psi \rangle \right|}^2$ .

A quantum collapse is responsible for externalization. The 50%/50% probability observation does not contradict with one copy being materialized at one position. See Subsection 3.2. for relevant discussion, and Subsection 3.1.2. for a possibility of quantum failure in the ungrammatical (1b) and Figure 2.

¹⁷MATLAB (an abbreviation of “matrix laboratory”) is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks (Wikipedia). SVD is a “data reduction tool” (Brunton, 2020), used to compress dimension. For example, a tensor multiplication yields a 4 by 4 matrix, which must be compressed to a 2 by 2 matrix to continue matrix multiplications with 2 by 2 matrix. SVD factorizes a matrix A into two orthogonal matrices V and U, between which a diagonal matrix Σ = S (symmetry, stretching, scaling, or growth factor) comes. Thus, A= UΣV. A crucial property of A is contained in Σ, which is used to obtain a compressed matrix of A. Unlike MS, in which specifier dimension reduction by decreasing the number of eigenvalues is proposed to compress matrices (Martin et al., 2019: 41), I use SVD to compress grown tensor-product matrices, following Strang (2016: 364-381), which states that (a) SVD separates any matrix into simple pieces, (b) when nearby pixels [matrices] are correlated (not random) the image [matrices] can be compressed [by SVD], and (c) when [SVD] compression is well done, you can’t see the difference from the original (ibid. 364-365).

¹⁸In QM, an entangled state takes place, i.e., two particles have no interaction, but they are somehow correlated (Zwiebach, 2016). Orús et al. (2017: 24; fn. 13) states that A’-chains formed by wh- and topic-IMs for example may involve entangled states in the Hilbert space. Possibly, an entanglement is available for A’-chain, which contains A-chain, whereas it is unavailable for A-chain, where chain members occupy A-positions uniformly. If a super-raising example involves an unfactorizable state, entanglement consideration is inescapable.

¹⁹It is incorrect to mention an example such as (i).

(i) It seems that Alice likes Bob.

It is so because it has a different lexical array, i.e., it contains a suffix attached to V, finite lower T, and complementizer that. The example (i) does not lead to a collapse in MS, since it is a different sentence from the infinitival one leading to Alice seems to like Bob [(1a)]. The example (11) is relatively appropriate example to indicate a distinct collapse within the same sentential geometry, except for the preposition for, which C_HL invokes as a last resort. Other examples for possible collapse are obtained from Uriagereka (2019: approximately at 15:23) as shown in (ii).

(ii) a. (There) was killed an emperor.

b. An emperor was killed.

In (iia), if the expletive there is deletable, (iia) and (iib) share the terms, and the collapse probability would be 50%/50%.

²⁰See Serrano (2020) for a plain introduction on how to interpret SVD geometrically.

²¹Given an X-bar geometry, where XP = phrase, Medeiros and Piattelli-Palmarini (2018: 5) introduced a rewrite table (ii), which leads to the Fibonacci matrix in (14).

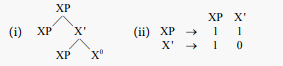
In (i), from top, XP consists of XP and X’, which consists of XP and X⁰. In a rewrite table (ii), the first row [1 1] indicates that XP is formed by adding one XP and one X’, the second row [1 0] shows that X’ is formed by using one XP and no X’. The Fibonacci matrix is also obtained by transforming a system of simultaneous equations as shown in (iii) into a formula $A_{uk}=u_{k+1}$ (Strang, 2016: 309).

(iii) $\{\begin{array}{l}{F}_{k+2}=F_{k+1}+F_k(\text{a})\\ F_{k+1}=F_{k+1}(\; b\; )\end{array}$

Strang (2011) called (iii-b) “a clever trick”. Given $u_k=\left[\begin{array}{c}{F}_{k+1}\\ F_k\end{array}\right]$ , $u_{k+1}=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]u_k$ .

²²Wolfram MathWorld; Fibonacci Number; https://mathworld.wolfram.com/FibonacciNumber.html

²³In fact, the SVD result of Chomsky matrices as well as matrices of other nodes is I. Linguistic structures are extremely stable and robust.

²⁴The identity property of occurrence matrices here forces a more restricted (i.e., absolute condition) version than chain uniformity (Chomsky & Lasnik, 1993). According to Chomsky and Lasnik (1993), a chain $\text{CH}=\left({\alpha }_1,\cdots ,{\alpha }_n\right)$ is a legitimate LF object if CH is uniform, where uniformity is a relational notion: the chain CH is uniform with respect to P (UN[P]) if each ${\alpha }_i$ has property P or each ${\alpha }_i$ has non-P (ibid.). In contrast, an absolute chain uniformity here requires ${\alpha }_i={\alpha }_{i+1}$ , i.e., complete identity.

²⁵The conjugate transpose ( ${\text{A}}^{†}$ ) can be indicated in several other ways, namely, A^H (“Hermitian matrix A”) = ${\text{<mover accent="true"> <mi> A </mi> <mo> ¯ </mo> </mover>}}^{\text{<mi> T </mi>}}$ (“transpose matrix of the conjugate of A”) = ${\text{A}}^{†}$ .

²⁶Suppose that one has a vector $\text{v}=\left[\begin{array}{c}1\\ i\end{array}\right]$ . If he uses a general multiplication to obtain a length squared $\Vert {\text{v}}^{\text{2}}\Vert$ , he ends up concluding that a nonzero vector has zero length because ${\text{v}}^2=\left[\begin{array}{cc}1& i\end{array}\right]\times \left[\begin{array}{c}1\\ i\end{array}\right]=1+i^2=1-1=0$ , which is a contradiction. To avoid such a contradiction, it is a rule to use a conjugate transpose ${\text{v}}^{†}$ in a complex vector multiplication, i.e., ${\text{v}}^{†}\text{v}=\left[\begin{array}{cc}1& -i\end{array}\right]\times \left[\begin{array}{c}1\\ i\end{array}\right]=1-i^2=1+1=2$ . Thus, $\Vert \text{v}\Vert =\sqrt{2}$ . See Strang (2016: 438) for an introduction of the reasoning.

²⁷This conforms with a commentary in Orús et al. (2017: 10) that “elsewhere M (merge) denotes the merger of two syntactic objects both of which are the results of previous merges in the derivation.”

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Arikawa, K. (2019). Graph Theory Teaches Us Something about Grammaticality. The Prague Bulletin of Mathematical Linguistics, 112, 55-82. https://doi.org/10.2478/pralin-2019-0002
[2]	Arikawa, K. (2020). Frustrated Nonphases as Catalysts for Phases—How Graph Theory Calculates Optimal Balance in Linguistic Fibonacci Trees and Graphs. Journal of Cognitive Science, 21, 253-348.
[3]	Bošković, Ž. (2013). Phases beyond Clauses. In L. Schuürcks, A. Giannakidou, & U. Etxeberria (Eds.), The Nominal Structure in Slavic and Beyond (pp. 75-128). Mouton de Gruyter. https://doi.org/10.1515/9781614512790.75
[4]	Bošković, Ž. (2014). Now I’m a Phase, Now I’m Not a Phase: On the Variability of Phases with Extraction and Ellipsis. Linguistic Inquiry, 45, 27-89. https://doi.org/10.1162/LING_a_00148
[5]	Brunton, S. (2020). Singular Value Decomposition (SVD): Overview. https://www.youtube.com/watch?v=gXbThCXjZFM
[6]	Carnie, A., & Medeiros, D. (2005). Tree Maximization and the Extended Projection Principle. Coyote Working Papers in Linguistics, 14, 51-55.
[7]	Chomsky, N. (1974). The Amherst Lectures. Unpublished Lecture Notes Distributed by Documents Linguistiques.
[8]	Chomsky, N. (1986a). Knowledge of Language: Its Nature, Origin, and Use. Praeger.
[9]	Chomsky, N. (1986b). Barriers. MIT Press.
[10]	Chomsky, N. (1995). The Minimalist Program. MIT press.
[11]	Chomsky, N. (2000). Minimalist Inquiries: The Framework. In R. Martin, D. Michaels, & J. Uriagereka (Eds.), Step by Step: Essays on Minimalist Syntax in Honor of Howard Lasnik (pp. 89-155). MIT Press. First Published in MIT Occasional Papers in Linguistics 15, 1998.
[12]	Chomsky, N. (2001). Derivation by Phase. In M. Kenstowicz (Ed.), Ken Hale: A Life in Language (pp. 1-52). MIT Press.
[13]	Chomsky, N. (2005). Three Factors in Language Design. Linguistic Inquiry, 36, 1-22. https://doi.org/10.1162/0024389052993655
[14]	Chomsky, N., & Lasnik, H. (1993). The Theory of Principles and Parameters. In J. Jacobs, A. von Stechow, W. Sternefeld, & T. Vennemann (Eds.), Syntax: An International Handbook of Contemporary Research (pp. 506-569). Mouton de Gruyter. (Reprinted in N. Chomsky (1995). The Minimalist Program (Current Studies in Linguistics 28), 13-127. Cambridge, MA: MIT Press). https://doi.org/10.1515/9783110095869.1.9.506
[15]	Guimarães, M. (2000). In Defense of Vacuous Projections in Bare Phrase Structure. In M. Guimarães, L. Meroni, C. Rodrigues, & I. S. Martin (Eds.), University of Maryland Working Papers in Linguistics (Vol. 9, pp. 90-115). Linguistics Department, University of Maryland.
[16]	Jakobson, R., & Halle, M. (1971). Fundamentals of Language. Mouton.
[17]	Martin, R. (2001). Null Case and the Distribution of PRO. Linguistic Inquiry, 32, 141-166. https://doi.org/10.1162/002438901554612
[18]	Martin, R., Orús, R., & Uriagereka, J. (2019). Towards Matrix Syntax. Catalan Journal of Linguistics: Special Issue, 27-44. https://doi.org/10.5565/rev/catjl.221
[19]	Medeiros, D. P. (2008). Optimal Growth in Phrase Structure. Biolinguistics, 2, 152-195. https://doi.org/10.5964/bioling.8639
[20]	Medeiros, D. P. (2012). Economy of Command. Ph.D. Thesis, The University of Arizona.
[21]	Medeiros, D. P., & Piattelli-Palmarini, M. (2018). The Golden Phrase: Steps to the Physics of Language. In A. J. Gallego, & R. Martin (Eds.), Language, Syntax, and the Natural Sciences (pp. 333-361). Cambridge University Press. https://doi.org/10.1017/9781316591529.018
[22]	Orús, R., Martin, R., & Uriagereka, J. (2017). Mathematical Foundations of Matrix Syntax. Cornell University.
[23]	Pierce, R. (2021). “Bra-Ket Notation” Math Is Fun. https://www.mathsisfun.com/physics/bra-ket-notation.html
[24]	Sato, F., & Matsushita, Y. (2007). Nami-No Shikumi: Koto-o Miru Butsurigaku [Mechanisms of Wave: Physics to See Phenomena]. Kodansha.
[25]	Serrano, L. (2020). Singular Value Decomposition (SVD) and Image Compression. https://www.youtube.com/watch?v=DG7YTlGnCEo
[26]	Smolensky, P. (1990). Tensor Product Variable Binding and the Representation of Symbolic Structures in Connectionist Networks. Artificial Intelligence, 46, 159-216. https://doi.org/10.1016/0004-3702(90)90007-M
[27]	Strang, G. (2011). Diagonalization and Powers of A. 18.06SC Linear Algebra, MIT OpenCourseWare. https://ocw.mit.edu/courses/18-06sc-linear-algebra-fall-2011/resources/lecture-22-diagonalization-and-powers-of-a
[28]	Strang, G. (2016). Introduction to Linear Algebra (5th ed.). Wellesley-Cambridge Press.
[29]	Uriagereka, J. (2016). On the Algorithmic Beauty of Language. A Lecture in IAI Colloquium, University of Maryland. https://www.youtube.com/watch?v=uMHvhiAhAUY
[30]	Uriagereka, J. (2019). Matrix Syntax (MS). Chair of Computational Mathematics. Logister Room at Deusto Tech, University of Deusto. https://cmc.deusto.eus/matrix-syntax-ms
[31]	Zwiebach, B. (2016). Quantum Physics I, Lecture 1: An Overview of Quantum Mechanics. MITOCW, 8.04. https://ocw.mit.edu/courses/physics/8-04-quantum-physics-i-spring-2016/index.htm