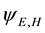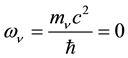Journal of Modern Physics
Vol.05 No.09(2014), Article ID:47363,13 pages
10.4236/jmp.2014.59091
Quantum-optical foundations of massive and massless particles
Burke Ritchie
Lawrence Livermore National Laboratory and Livermore Software Technology Corporation, Livermore, USA
Email: ritchie@lstc.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 April 2014; revised 2 May 2014; accepted 29 May 2014
ABSTRACT
A source of the divergences in QED is proposed, and a theory in which the Lamb shift and elec- tron’s anomalous magnetic moment are calculated free of divergences is reviewed. It is shown that Dirac’s equation for a relativistic electron can be inferred from a Lorentz invariant having the form of the Lorentz gauge equation, 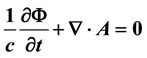 , on identifying a carrier-wave energy
, on identifying a carrier-wave energy 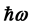 with the electron’s rest mass energy mc2, the vector potential’s polarization vector with Pauli’s vector
with the electron’s rest mass energy mc2, the vector potential’s polarization vector with Pauli’s vector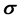 , and the envelops of the scalar and vector potentials with the four components of Dirac’s vector wave function. The same methodology is used to infer relativistic equations of motion hav- ing the Dirac form for a neutrino accompanied by ab initio neutrino-matter interaction terms. Then it is shown that the theory, which comprises Dirac’s equation plus the relativistic equations of motion for the neutrino, supports binding on a nuclear scale of energy and length. The experi- mentally observed weakness of the interaction energy of free neutrinos and matter is due to the smallness of the rate of tunnelling of free neutrinos through a potential barrier which exists in the interaction of free neutrinos and matter. Models are also proposed for the proton and neutron, and good agreement is obtained for the neutron-proton rest mass energy difference in view of the approximations made to solve the appropriate equations of motion.
, and the envelops of the scalar and vector potentials with the four components of Dirac’s vector wave function. The same methodology is used to infer relativistic equations of motion hav- ing the Dirac form for a neutrino accompanied by ab initio neutrino-matter interaction terms. Then it is shown that the theory, which comprises Dirac’s equation plus the relativistic equations of motion for the neutrino, supports binding on a nuclear scale of energy and length. The experi- mentally observed weakness of the interaction energy of free neutrinos and matter is due to the smallness of the rate of tunnelling of free neutrinos through a potential barrier which exists in the interaction of free neutrinos and matter. Models are also proposed for the proton and neutron, and good agreement is obtained for the neutron-proton rest mass energy difference in view of the approximations made to solve the appropriate equations of motion.
Keywords:
Divergence-free electrodynamics, radiant aspect, material aspect, nuclear binding

1. Introduction
In previous work [1] the charge of the electron, e, but not its mass, m, was inferred from an anti-propagating so- lution of Maxwell’s equations, suggesting that an electron is a localized, bundled form of radiant energy. This result suggests that matter and light are not necessarily separate objects requiring separate field theories for their description. In fact there is strong evidence for this view in the form of experimental observations of the atomic Lamb shift and the electron’s anomalous magnetic moment. Although the quantized electromagnetic field is used to describe these phenomena, theory and experiment agree only after theory is renormalized to account for the permanent nature of radiation in the structure of matter―renormalization of the mass of a free electron to account for a continuous emission and reabsorption of a photon [2] ―suggesting that matter-free photon fields or photon-free matter fields do not exist in nature and are the origin of the divergences which plague both QED and QFT.
I pursue a mixed matter-light concept using a quantum-optical methodology firstly by inferring Dirac’s equa- tion for a relativistic electron from the Lorentz gauge equation, which is the Lorentz invariant found from the scalar product of the 4-gradient and the electromagnetic 4-potential,
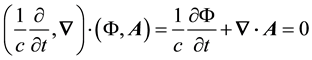 , (1)
, (1)
as I show in the next section. Dirac’s desiderata for his equation is that it should satisfy the energy-momentum relationship of special relativity and that it should be compatible with the equation of continuity, which is the Lorentz invariant found from the scalar product of the 4-gradient and the 4-current,
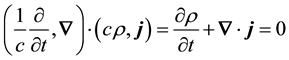 . (2)
. (2)
Notice that matter and light are not separated in classical field theories. For example Maxwell’s wave equa- tion follows by requiring that Ampere’s equation should be compatible with the equation of continuity given by Equation (2).
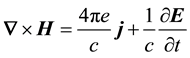 , where Equation (2) is recovered by finding the divergence of both sides of Ampere’s
, where Equation (2) is recovered by finding the divergence of both sides of Ampere’s
equation and using Coulomb’s equation,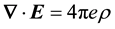 .
.
To be sure light and matter are inextricably interwoven in classical electromagnetic theory. The matter con- tributions were originally understood using classical mechanics and then were later updated using quantum me- chanics to arrive at an overall semiclassical theory (classical theory of radiation combined with a quantum theory of matter). This situation changed when Dirac quantized the free radiation field to calculate the Einstein A and B coefficients for emission and absorption of radiation as discrete photons by matter [3] . Dirac’s theory failed when it was applied to the Lamb shift over twenty years later, leading to a renormalization methodology in order to obtain agreement of theory with Lamb’s experimental data [2] .
It is possible to interpret Lamb’s experiments not as the result of the interaction of free photons and matter, which is the standard interpretation following the success of renormalization theory, but rather as an observation that radiation is a permanent part of the structure of matter, which of course is not compatible with the prior de- velopment of the quantum theory of matter as a radiation-free theory. It is possible to criticize QED, notwith- standing its success, on the basis not only that theory must be augmented by physical argument and ad hoc ma- thematical procedures to obtain agreement with experiment but that its pioneers failed to confront Lamb’s expe- riments in the first place as revolutionary for the structure of matter and decided to use the matter-free photon theory and the photon-free matter theory which were on hand [2] [3] .
The removal of divergences in QED requires renormalization schemes based the notion that a photon is al- ways present in the structure of a free electron [2] such that the electron’s mass is renormalized by addition of an electromagnetic contribution to the electron’s material mass, m. This result suggests that new relativistic equa- tions of motion should be sought which describe the electron’s radiant aspect in analogy to Dirac’s equation, which describes the electron’s material aspect. In QED a quantized form of the free classical radiation field is used which is external to an electron such that radiative shifts are calculated based on the logical and mathema- tical paradigm of a continuous emission (creation) and reabsorption (annihilation) of a photon. Although the theory works beautifully for the emission and absorption of radiation in discrete quanta, it leads to an atomic energy-level shift which diverges linearly in the photon’s frequency, 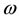 , requiring a renormalization procedure to remove the divergent contribution to the energy shift [2] . It is my thinking here that new equations of motion should be sought to account for an electron’s radiant aspect as an intrinsic property of an electron such that Maxwell’s equations either in classical or quantized form will fail (in absence of renormalization schemes) to describe the radiative contribution to atomic structure.
, requiring a renormalization procedure to remove the divergent contribution to the energy shift [2] . It is my thinking here that new equations of motion should be sought to account for an electron’s radiant aspect as an intrinsic property of an electron such that Maxwell’s equations either in classical or quantized form will fail (in absence of renormalization schemes) to describe the radiative contribution to atomic structure.
These radiant-aspect equations, which are given explicitly in the next section, are inferred from the Lorentz invariant found from the scalar product of a renormalized 4-gradient and a postulated 4-potential in analogy to Equation (1),
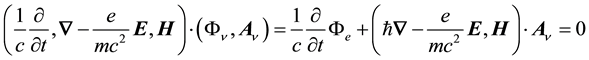 , (3)
, (3)
(where the notation 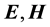 means electric or magnetic field respectively) such that the scalar product of the re-
means electric or magnetic field respectively) such that the scalar product of the re-
normalized 4-gradient, 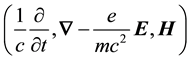 , and the electromagnetic 4-current,
, and the electromagnetic 4-current, 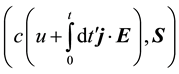 ,
,
gives the electromagnetic equation of continuity,
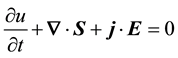 , (4)
, (4)
since the scalar product of the 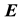 or
or 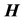 with
with 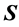 vanishes, where
vanishes, where 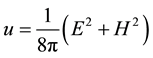
energy density and 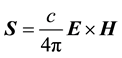
aspect equations inferred from Equation (3) are used to calculate the Lamb shift [4] and the electron’s anomal- ous magnetic moment [5] , it is found that the new results are free of divergences. Dirac required his equation for a relativistic electron to be compatible with the material equation of continuity given by Equation (2). It appears from my work that a complete description of a relativistic electron, in which its radiant aspect responsible for the Lamb shift and its anomalous magnetic moment are properly understood without needing to remove infinite contributions using renormalization schemes, should also comprise equations of motion which are compatible with the electromagnetic equation of continuity given by Equation (4).
The details of this theory are given in the next section. Then in the following sections the theory is applied in an exploratory manner to nuclear binding. Thus it appears that a theory free of divergences in electron and atomic phenomena also includes a theory of nuclear phenomena.
2. Quantum-optical methodology for massive and massless particles
2.1. Equation of motion for the material aspect of matter (Dirac’s equation)
We may use Lorentz’ equation [Equation (1)] to elucidate the structural relationship of Dirac’s equation for a relativistic electron with the spinorial form of Maxwell’s equation, a subject which has been studied conti- nuously [6] - [9] since Dirac’s equation first appeared in 1928 [10] . The scalar and vector potentials can be writ- ten in the form of carrier-wave expansions for an assumed dominant frequency component, thusly,

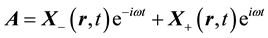
On substituting Equation (5) into Equation (1) and separately setting the coefficients of the exponential fac- tors equal to zero, one obtains,
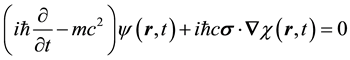
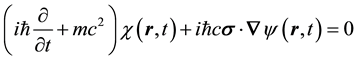
which are identically Dirac’s pair of first-order equations for a free electron on setting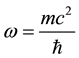
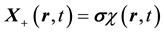
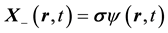
functions are the Dirac two-component spinors. Hence one has a Lorentz-invariant relativistic equation of mo- tion for a material particle (MEOM) if the carrier-wave frequency belonging to the posited 4-potential is equal to the rest-mass energy of the material particle divided by
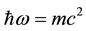
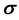
will be given below for its interaction with the familiar electromagnetic 4-potential, 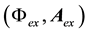
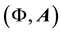
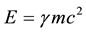
Lorentz factor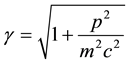
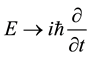
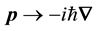
should be compatible with the material equation of continuity given by Equation (2). The latter demand is satis- fied by Dirac’s equation, giving a current,
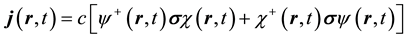
where the superscripts denote Hermitian conjugates.
2.2. Equation of motion for the radiant aspect of matter (REOM)
As with the electron the posited 4-potential given in Equation (3) can be written in the form of carrier-wave ex- pansions,
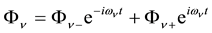
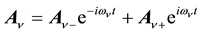
from which on substituting Equation (8) into Equation (3) and separately setting the coefficients of the exponen- tial factors equal to zero, we obtain,

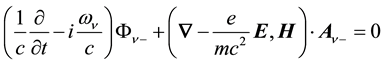
On setting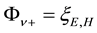
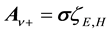
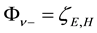
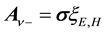
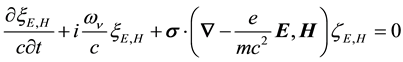
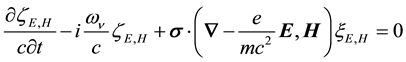
Writing 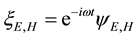
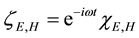
and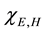
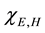
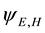
equations for the electric and magnetic radiant-particle wave functions which have the Helmholtz form,
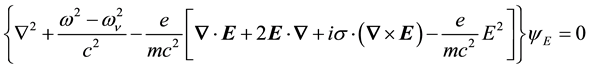
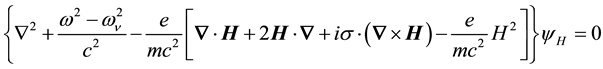
where we have used the identity,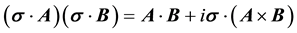
in physical applications to calculate a divergence-free Lamb shift [4] and electron’s anomalous magnetic mo- ment [5] .
Notice that in Equation (11) external electromagnetic fields and not external electromagnetic potentials occur such there is no question of a gauge dependence of matter-light interactions in the electron’s REOM. The suc- cess of the use Equation (11b) to calculate divergence-free radiative properties of matter [4] [5] suggests that the concept of radiation as a permanent part of the structure of matter is a valid one. Recall that this is identically the concept of mass renormalization used in standard QED to remove infinite contributions to the electron’s energy arising from the logic, which appears to be unphysical, that first-quantized states of matter exist which are total- ly free of radiation. As I have shown here it is possible to present a theory in which the electron does not exist in a bare or radiation-free state and whose material and radiant properties are described by a pair of relativistic, Lorentz-invariant first-quantized MEOM and REOM respectively.
As shown below in the electric-field and magnetic-field equations of motion with second-order Helmholtz
form [Equation (11)], the same-parity, 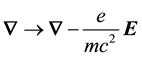
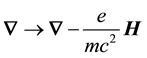
contribute, among other terms, all four of Maxwell’s equations as interaction terms, the same parity addition
vector contributing 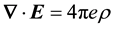
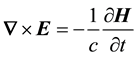
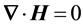
The radiation-matter interaction terms are guaranteed to be gauge invariant by depending on the electromag- netic fields rather on the the electromagnetic potentials. Our approach here has been to face Lamb’s observation that the structure of matter has a permanent radiative component by finding first-quantized equations of motion for the radiant aspect of matter, in analogy to Dirac’s first-quantized equation of motion for the material aspect of matter. It seems remarkable that an established REOM does not already exist in the literature. The omission seems to follow from the neglect of a requirement that a complete relativistic-electron theory should be compa- tible with the electromagnetic equation of continuity [Equation (4)] as well as with the material equation of con- tinuity [Equation (2)]. Dirac required only that his equation be compatible with the material equation of continuity.
In summary the renormalization of the 4-gradient using 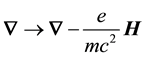
in which the radiant particle can be identified with the photon since the REOM gives a divergence-free theory of the Lamb shift [4] and of the electron’s anomalous magnetic moment [5] . On the other hand the renormalization
of the 4-gradient using 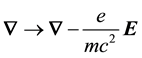
section.
2.3. Dirac’s equation (MEOM) with external electromagnetic interactions
Finally it remains to follow through with the “quantum optical” derivation of Dirac’s equation for the material particle (MEOM) in the presence of external electromagnetic potentials, which is given by
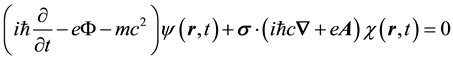
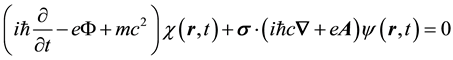
Notice that Equation (12) follow from Equation (1) on renormalizing the 4-gradient as follows,
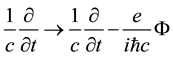
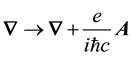
4-potential has been dropped.
3. Solution of Equation (11a) and Equation (12) as coupled equations of motion for the radiant and material aspects of matter
The equations of motion for the radiant and material properties of matter are given by Equation (11) and Equa- tion (12)] respectively. Equation (11b) and Equation (12) were used in earlier work [4] [5] to calculate a diver- gence-free Lamb shift and divergence-free electron’s anomalous magnetic moment. Equation (11a), which is the radiant equation of motion with electric-field interaction (REOMEF), is studied here. These equations are writ- ten as follows,
REOMEF:
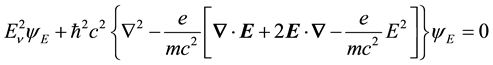
MEOM (Dirac’s equation in second-order form):
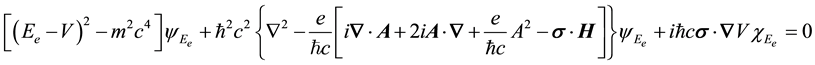
where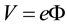
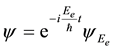
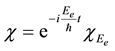
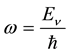
appropriate for a mass-0 particle.
Models for a proton and neutron (Figures 1-3) are constructed by summing the electric field in the REOMEF and the potential in the MEOM over the electric fields and potentials respectively arising from two positrons and one electron (proton model) and over two positrons and two electrons (neutron model). In the MEOM the short-range repulsion due to the spin-orbit interaction is overcome by short-range attraction due to the magnetic interaction,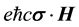
The REOMEF with MEOM interaction terms in the REOMEF are given by the summed electric fields arising from the quantum charge densities of bare electrons and bare positrons. 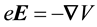
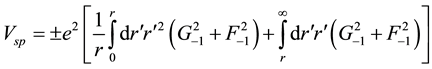
for the interaction of particles with the same (+) or opposite (?) charges and where the electronic density is that inferred from the MEOM using the large and small components of the MEOM wave function for a bare electron
(or bare positron) 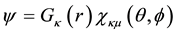
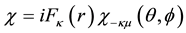
the right sides of the minima in Figure 1 reflect a larger degree of repulsive spin-orbit coupling (which for 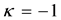
The MEOM with REOMEF interaction terms in the MEOM are given by the A2 and Pauli 
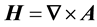
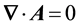
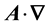
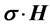
The vector potential is calculated from Maxwell’s equation,
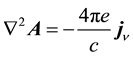
where the current arises from the radiant particle’s spin, 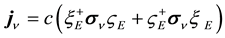
Equation (10) on using an equation of continuity for the electron’s (or positron’s) radiant aspect
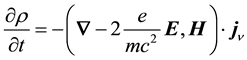
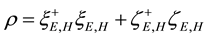
conjugate. Hence the spinor analysis for a REOMEF particle, for which 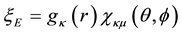
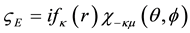
The Cartesian components of the current for 
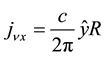
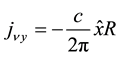
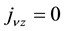
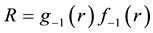
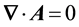
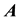
The magnetic field is found by taking the curl of both sides of Equation (15),
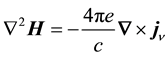
Only the diagonal or z-component of 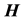
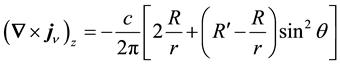
tion (16),
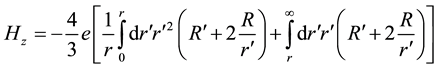
Proceeding heuristically the radial equations (for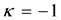
trial forms 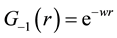
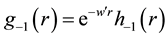
ticle respectively, where w = w' and in Equation (18a) below the contribution given by 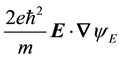
luated approximately by replacing it with 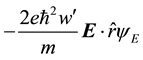
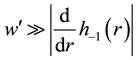
“small” components are calculated using the trial forms, 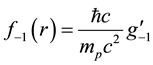
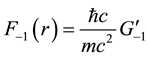
diant and bare electron respectively, where mp is the proton mass, which is the only empirical parameter in the calculation. The minimum energy, as we shall see below, occurs for w approximately equal to the reciprocal of
the proton Compton wavelength, 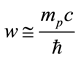
tional form for 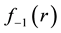
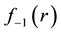
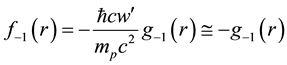
which the large denominator mpc2 is cancelled by the numerator 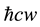
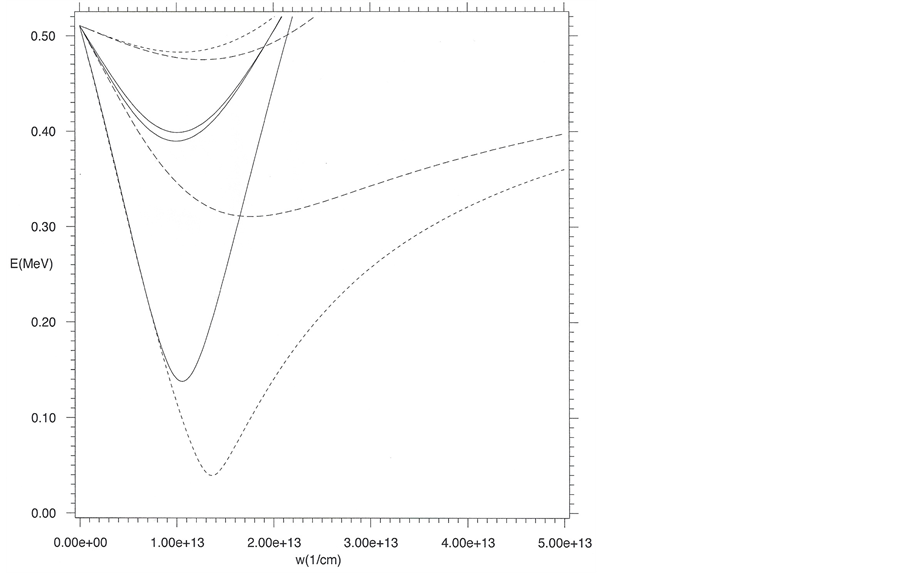
Figure 1. Dirac energies versus variational parameter w from Equation (13b). The proton model comprises the three lower curves as follow. Short dashed: radiant positron 1 energy versus variational parameter w. Long dashed: radiant positron 2 energy versus variational parameter w. Solid: radiant electron energy versus variational parameter w. The neutron model comprises the upper four curves as follows. Short dashed: radiant positron 1 energy versus variational parameter w. Long dashed: radiant positron 2 energy versus variational parameter w. Upper solid: radiant electron 1 energy versus variational parameter w. Lower solid: radiant electron 2 energy versus variational parameter w. The more steeply rising energy curves on the right sides of the minima reflect a larger degree of repulsive spin-orbit coupling, which for an attractive V is repulsive and for a repulsive V is attractive for 
force-carrier picture of QCD.
Once the derivative operation indicated in the interaction contribution, 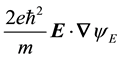
ly evaluated as outlined above Equation (11a) has the Schroedinger form,
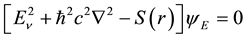
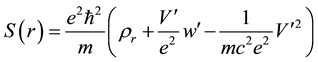
where in Equation (18b) 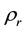
I posit that negative imaginary energy states are physically-interpretable in the sense that they are temporally bound and are therefore “confined” since transition rates vanish by destructive interference of contributions to
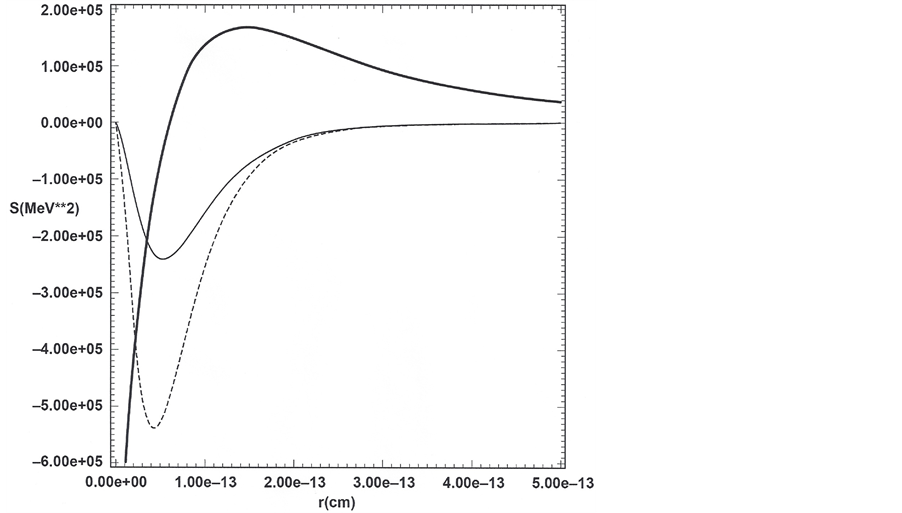
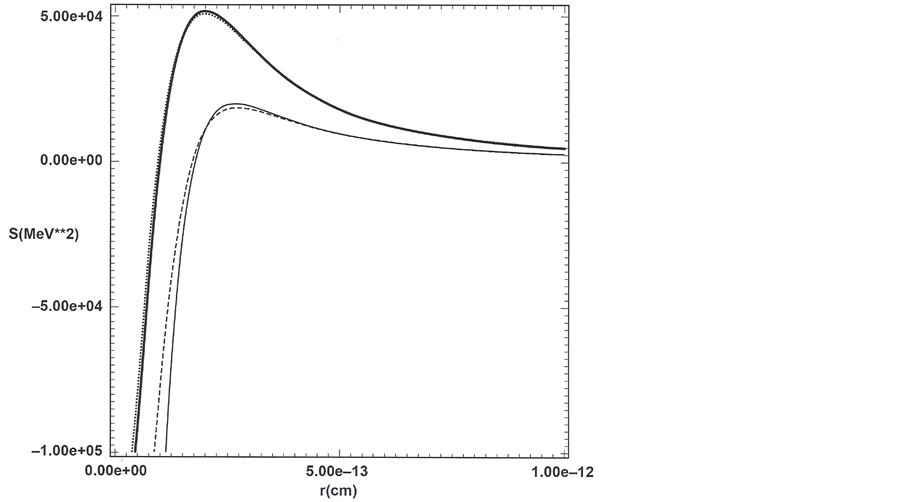
Figure 2. Proton model with reference to Equations (18) and (19) and Table 1. Light solid (curve 1): S(r) in Equation (18b) versus r corresponding to the minimum of radiant positron 1 energy in Figure 1 for radiant-particle variational parameter w' = 3.5w and for negative-imaginary energy inferred from Equation (19) for n = 0 equal to 0.315 GeV. Dashed (curve 2): S(r) in Equation (18b) versus r corresponding to the minimum of the radiant positron 2 energy in Figure 1 for radiant-particle variational parameter w' = 2.7w and for negative-imaginary energy inferred from Equation (19) for n = 0 equal to 0.520 GeV. Thick solid (curve 3): S(r) in Equation (18b) versus r corresponding to the minimum of the radiant electron energy in Figure 1 for radiant-particle variational parameter w' = 2.2w and for negative-imaginary energy inferred from Equation (19) for n = 0 equal to 0.103 GeV. S(r) is calculated from the sum of interaction terms given on the right side of Equation (18b). Curves 1 and 2 go into the origin by cancellation in the first terms on the right side of Equation (18b) comprising one repulsive and one attractive interaction for each curve. The cancellation of interaction terms finite at the origin occurs only because the same w is used for all three radiant-particle trial wave functions. Curve three has a different shape due to the sum of two at- tractive interactions.
transition-rate matrix elements between temporally bound and temporally harmonic states. (Notice that imagi-
nary-energy states of the Dirac Coulomb problem, for which 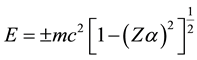
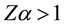
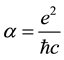
tion.
Standard WKB theory [11] [12] can be used to estimate the energy levels in the negative region of the squared energy by using
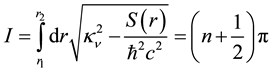
where 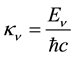
square-root sign is positive.
In the following discussion the following nomenclature will be used. The bound solutions emerging from the REOMEF, which is coupled to the MEOM, will be referred to as radiant particles (charge-0, mass-0, spin-1/2 particles). The bound solutions emerging from the MEOM, which is coupled to the REOMEF, will be referred to as radiant electrons and radiant positrons as distinguished from bare electrons and bare positrons, which are
Figure 3. Neutron model with reference to Equations (18) and (19) and Table 2. Long dashed: S(r) in Equation (18b) versus r corresponding to the minimum of the radiant positron 1 energy in Figure 1 for radiant variational parameter w' = 1.2w and for negative-imaginary energy inferred from Equation (19) for n = 0 equal to 0.315 GeV. Light solid: S(r) in Equation (18b) versus r corresponding to the minimum radiant positron 2 energy in Figure 1 for radiant-particle variational parameter w' = 1.0w and for negative-imaginary energy inferred from Equation (19) for n = 0 equal to 0.520 GeV. Thick solid: S(r) in Equation (18b) versus r corresponding to minimum radiant electron 1 energy in Figure 1 for radiant-particle variational parameter w' = 2.2w and for negative-imaginary energy inferred from Equation (19) for n = 0 equal to 0.103 GeV. Short dashed: S(r) in Equation (18b) versus r corresponding to the minimum of radiant electron 2 energy in Figure 1 for radiant- particle variational parameter w' = 2.3w and a positive squared energy of 0 such that the zero-energy state is unstable against dissociation into a bare electron and neutrino with lifetime of 1.15 × 103 s. As the squared energy well becomes narrower, negative squared energy states stable against dissociation are popped into the squared positive energy region unstable against dissociation. All curves have the shape of curve 3 in Figure 1 due to the sum of one repulsive and two attractive interactions for each radiant particle.
the solutions of the MEOM uncoupled to the REOMEF. The radiant electrons and radiant positrons have totally different binding characteristics than bare electrons and bare positrons as I discuss in detail as follows.
It is possible to find bound states for two radiant positrons and one radiant electron to give a model for the proton by finding the variational parameter w' for the REOMEF trial wave functions to give the three lower MEOM energy minima shown in Figure 1 which at the same time correspond to the three REOMEF squared- energy curves calculated from Equation (18b) and shown in Figure 2, whose negative-imaginary WKB energies sum to give a good approximation to the proton’s rest-mass energy (Table 1), neglecting the three lower Dirac energy minima of Figure 1, which are on the MeV scale. The balance between spin-orbit repulsive interactions and magnetic attractive interactions is tipped in favor of attraction using 760 radiant particles associated with the first bare positron, 450 radiant particles associated with the second bare positron, and 2130 radiant particles as- sociated with the bare electron. The reader should keep in mind that I am solving two coupled homogeneous equations such that the energies of each is independent of the wave-function norm. The interaction terms in each equation however does depend of the wave-function norm for each equation. Dirac’s equation (MEOM) is nor- malized in the usual way to one particle (electron or positron). The radiant equation of motion (REOMEF) is normalized however to N radiant particles such that the back interaction in the MEOM (interaction of bare ma- terial particles with radiant particles) is weighted by N, which is adjusted along with the variational parameters to give the minima in the MEOM energy curves shown in Figure 1.
The scaling of squared energies in each MEOM to give a balance between spin-orbit repulsion and magnetic
attraction has the form 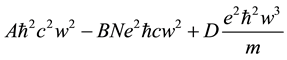
Table 1. Negative-imaginary protonic energies inferred from Equation (19) for n = 0 for the variational parameters used in the REOMEF trial wave functions. The same w is used for all three radiant electrons and radiant positrons and is varied, along with the number of REOMEF radiant particles (N as discussed in the text) associated with each radiant electron or radiant positron, to give the minima shown in Figure 1.
for N radiant particles determining the strength of the magnetic field given by Equation (17) due to the radiant- particle current and spin-orbit repulsion where A, B, and D are dimensionless constants from the calculation. Notice the w2 scaling of the magnetic attraction (in contrast to Coulombic terms which scale as 2 mc2e2w) mak- ing it competitive with the kinetic energy term scaling as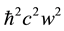
The upper four MEOM minima shown in Figure 1 are for the binding of two radiant positrons and two ra- diant electrons requiring 1300, 1700, 1000, and 1000 radiant particles associated with bare positron1, bare posi- tron 2, bare electron 1, and bare electron 2 respectively in order for magnetic attraction to overcome spin-orbit repulsion, the latter of which is stronger in the neutron model than in the proton model. At the same time the four MEOM minima correspond to the four REOMEF squared-energy curves calculated from Equation (18b) and shown in Figure 3, whose negative-imaginary WKB energies sum to give a good approximation to the pro- ton’s rest-mass energy (Table 2), neglecting the four upper Dirac energy minima of Figure 1, which are on the MeV scale. Notice again that the rest-mass energy difference between the neutron and proton is given on the MeV scale, as stated above, by the difference of the four upper Dirac energy minima and the three lower Dirac energy minima shown in Figure 1.
Standard WKB theory [11] can be used to estimate the tunneling rate through the barrier, whence
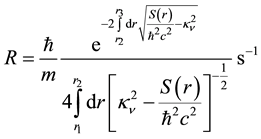
where the integration limits in the exponential term are over the barrier width.
For the value of w giving the minimum Dirac energy in Figure 1 an energy 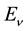
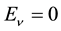
In the proton model (Figure 2) comprising two radiant positrons and one radiant electron only the radiant- electron curve has a squared-energy barrier and thus can support positive-squared-energy states which are un- stable against dissociation into a bare electron and the radiant particle, which can be identified with a neutrino from experimental observation of neutron beta decay. The experimentally observed weakness of the interaction
Table 2. Negative-imaginary neutronic energies inferred from Equation (19) for n = 0 for the variational parameters used in the REOMEF trial wave functions. The same w is used for all four radiant electrons and radiant positrons and is varied, along with the number of REOMEF radiant particles (N as discussed in the text) associated with each radiant electron or radiant positron, to give the minima shown in Figure 1. The w' parameter as multiple of w is chosen to give the same proton rest- mass energies as are given in Table 1. The lifetime inferred from Equation (20) is also given in this table for the zero energy of one of the radiant electrons. The experimentally observed weakness of the interaction energy of free neutrinos and matter is due to the smallness of the rate of tunnelling of free neutrinos through a potential barrier which exists in the interaction of free neutrinos and matter such that the weak interaction energy of neutrinos and matter can be estimated from the uncertainty principle
energy of free neutrinos and matter is due to the smallness of the rate of tunnelling of free neutrinos through a potential barrier which exists in the interaction of free neutrinos and matter such that the weak interaction energy of neutrinos and matter can be estimated from the uncertainty principle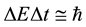
I should comment here on the scaling of the interaction terms in the two coupled equations so that readers feel comfortable with the nuclear-scale binding found in these calculations. 
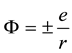
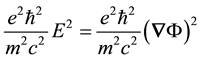
can support bound states of the REOMEF. The interaction scales according to the quantum expectation value of
the attractive interaction term, 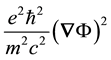
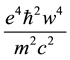
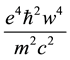
with increasing w the kinetic energy (first term in the above operator) scaling as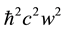
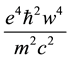
Compton wavelength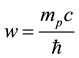
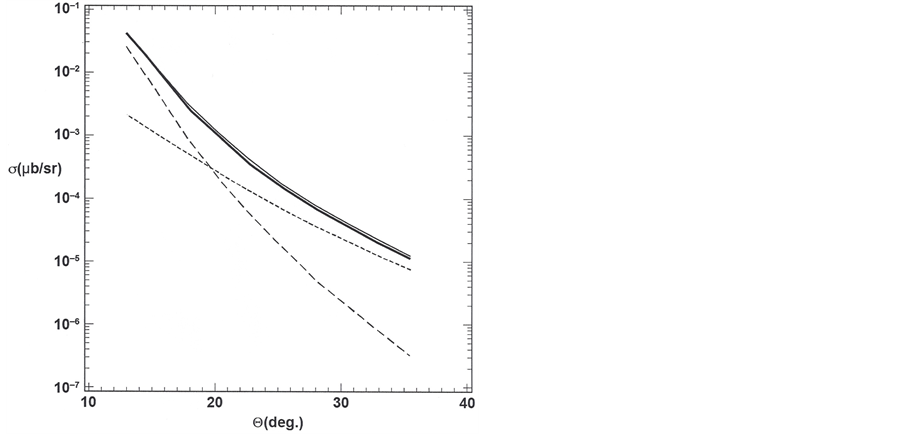
Finally Figure 4 show results for the e−, model elastic scattering cross section in the Born approximation as compared with measured results for e?, p+ elastic scattering [12] . This result depends on choosing 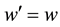
ing as 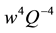
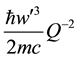
tum transfer, such that, as shown in Figure 4, the Coulombic interactions are dominant at the small angles and the magnetic interaction is dominant at the large angles. The two contributions add coherently to give the total cross section, which is compared with the measured cross section [12] . The theoretical results for the lower beam energies of [12] are not as good due to an overestimation of the Coulombic contributions at the small an- gles. The beginning of this disagreement is seen in Figure 4 due to too rapid a rise in the Coulombic contribu- tion at the smallest angles.
Figure 4. Electron-proton elastic-scattering cross section in the GeV regime. Thin solid: measured elastic e?, p+ scattering cross section for a beam energy of 5.494 GeV [12] . Thick solid: calculated elastic e?, model p+ scattering cross section us- ing Born theory. Long dashed: calculated cross section using only Coulombic interactions of the target with the scattering electron. Short dashed: calculated cross section using only the magnetic interaction of the target with the scattering electron.
4. Conclusion
Equations of motion for the radiant properties of matter (REOM) have been presented based on Lamb’s experi- ments showing that the energy levels of an atom are permanently shifted by radiation. The REOM are posited as relativistic equations of motion which are compatible with the electromagnetic equation of continuity in analogy to Dirac’s equation for the material properties of matter (MEOM), which is compatible with the material equa- tion of continuity. The REOM with electric-field interaction (REOMEF) supports the binding of radiant matter on a GeV energy scale and Fermi-unit length scale. Bound states of the REOMEF which are stable against dis- sociation occur in a region of negative squared energy, for which the energy is negative imaginary, such that binding occurs both in time (or in the 4-space scaled time ct) and space. Since transitions rates vanish between temporally bound and temporally harmonic states, bound matter may not be broken up into individual constitu- ents and may be considered to describe a form of confinement found in QCD Bound states of the REOMEF which occur in a region of positive squared energy are unstable against dissociation into a bare electron or bare positron and a mass-0, spin-1/2, neutral particle which I have posited to be a neutrino. The theory is used to con- struct a model for the proton which shows good agreement with the proton rest-mass energy and measured e?, p+ elastic-scattering cross section. A model for the neutron is also constructed and the neutron-proton rest-mass difference agrees well with the observed value in view of the approximations made to solve the appropriate equ- ations. The neutron model invites new experiments to look for stimulated beta decay as given by the reaction,
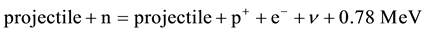
Acknowledgements
The author is grateful to T. Scott Carman for supporting this work. He is grateful to Professor John Knoblock of the University of Miami for seminal discussion. This work was performed under the auspices of the Lawrence Livermore National Security, LLC (LLNS) under Contract No. DE-AC52-07NA27344.
References
- Ritchie, B. (2008) Journal of Modern Optics, 55, 2003-2009. http://dx.doi.org/10.1080/09500340801947595
- Louisell, W. (1973) Quantum Statistical Properties of Radiation. Wiley, New York.
- Dirac, P.A.M. (1927) Proceedings of the Royal Society A (London), 114, 243-265. http://dx.doi.org/10.1098/rspa.1927.0039
- Ritchie, B. (2007) Optics Communications, 280, 126-132. http://dx.doi.org/10.1016/j.optcom.2007.08.003
- Ritchie, B. (2008) Optics Communications, 281, 3492-3494. http://dx.doi.org/10.1016/j.optcom.2008.03.002
- Ritchie, B. (2006) Optics Communications, 262, 229-233. http://dx.doi.org/10.1016/j.optcom.2005.12.063
- Darwin, C.G. (1928) Proceedings of the Royal Society A, 118, 654-680. http://dx.doi.org/10.1098/rspa.1928.0076
- Laporte, O. and Uhlenbeck, G. (1931) Physical Review, 37, 1380-1397. http://dx.doi.org/10.1103/PhysRev.37.1380
- Armour Jr., R. (2004) Foundations of Physics, 34, 815-842. http://dx.doi.org/10.1023/B:FOOP.0000022188.90097.10
- Dirac, P.A.M. (1928) Proceedings of the Royal Society A (London), 117, 610-624. http://dx.doi.org/10.1098/rspa.1928.0023
- Bethe, H.A. and Salpeter, E.E. (2008) Quantum Mechanics of One- and Two-Electron Atoms. Dover, New York, 238.
- Christy, M.E., et al. (2004) Physical Review C, 70, Article ID: 015206. http://dx.doi.org/10.1103/PhysRevC.70.015206