Applied Mathematics
Vol. 3 No. 2 (2012) , Article ID: 17394 , 3 pages DOI:10.4236/am.2012.32026
A Nonstationary Halley’s Iteration Method by Using Divided Differences Formula
Department of Mathematics, Faculty of Science, University of Aleppo, Aleppo, Syria
Email: Ide1112002@Yahoo.ca
Received July 22, 2011; revised August 13, 2011; accepted August 21, 2011
Keywords: Nonstationary; Iterative Method; Hally’s Formula; Divided Differences
ABSTRACT
This paper presents a new nonstationary iterative method for solving non linear algebraic equations that does not require the use of any derivative. The study uses only the Newton’s divided differences of first and second orders instead of the derivatives of (1).
1. Introduction
In order to solve the nonlinear algebraic equations of the form.
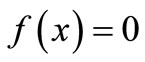 (1)
(1)
where f(x) is a known function. Let α be a simple real root of the Equation (1) and let x0 an initial approximation to α. An iterative method [1] for solving the Equation (1), in form of sequence of approximations by using the formula:
 (2)
(2)
The most popular iterative process, is the Newton’s one-point process
 (3)
(3)
We know that Newton’s method is quadratically convergent, this method requires two operations at each iteration, evaluation of f(xn) and . Tamara Kogan, Luba Sapir and Amir Sapir [1] illustrate that the secant method is classical 2-point iterative process which does not require use of any derivative, and they defined this method as follows
. Tamara Kogan, Luba Sapir and Amir Sapir [1] illustrate that the secant method is classical 2-point iterative process which does not require use of any derivative, and they defined this method as follows
 (4)
(4)
where  are two successive approximations to a and
are two successive approximations to a and  is the first-order divided difference. The construction of many iterative processes is based on Newton’s divided difference formula, where
is the first-order divided difference. The construction of many iterative processes is based on Newton’s divided difference formula, where
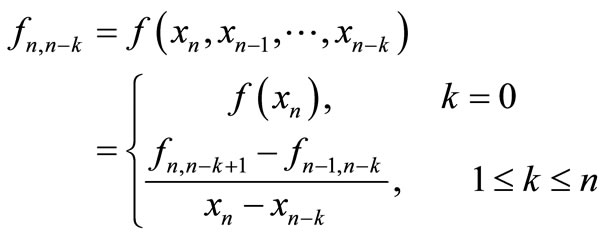 (5)
(5)
Is a divided difference of order K. Kogan [2] extended the secant method as follows:
 (6)
(6)
where ,
,  ,
,  are three successive approximations to the simple root α of (1), Many iterative processes of third-order have been studied, Tamara Kogan, Luba Sapir and Amir Sapir in [1] suggest the following iterative method for approximation of a simple root α of (1):
are three successive approximations to the simple root α of (1), Many iterative processes of third-order have been studied, Tamara Kogan, Luba Sapir and Amir Sapir in [1] suggest the following iterative method for approximation of a simple root α of (1):
 (7)
(7)
As a nonstationary iterative process, (i.e. the function F depends on the number of iteration):
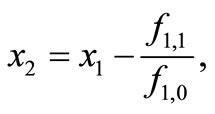
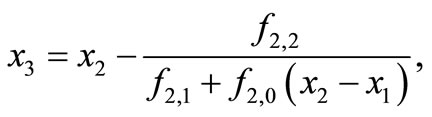

In our study, we suggest a new iterative method for approximation of a simple root α of (1) by using only the Newton’s divided differences of first and second orders instead of the derivatives of the first and second order.
2. The Principle of the Nonstationary Halley’s Iteration Method by Using Divided Differences Formula
We suggest the following iterative method for approximation of a simple root α of (1):

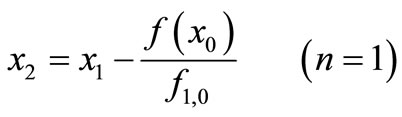 (8)
(8)
It is clear that (8) is a nonstationary iterative process,



The iterative method (8) is the Hally’s formula, see [3], but we take instead of  and
and , successively, the divided differences
, successively, the divided differences  and
and  (of first and second orders only), hence we have two types of errors:
(of first and second orders only), hence we have two types of errors:
1) Cubic error comes from the Hally’s iterative processes (of third-order).
2) Error comes from the approximation of divided differences.
The following example (given by [1] also), illustrates the suggested method
3. The Convergence of the Method
Let  be the error at the iteration, then
be the error at the iteration, then . Let the function :
. Let the function :
 (9)
(9)
Then,
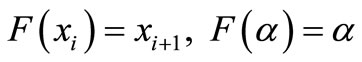 (10)
(10)
and
 (11)
(11)
Expending F(x) about  and using (9) and (10) we obtain
and using (9) and (10) we obtain
 (12)
(12)
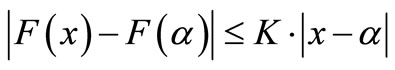 (13)
(13)
where,
 (14)
(14)
For , and using (13) we obtain,
, and using (13) we obtain,
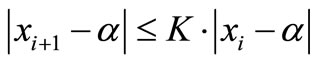 (15)
(15)
This yields that  and this proves the required.
and this proves the required.
4. Example 1
Consider the equation given in [1]:
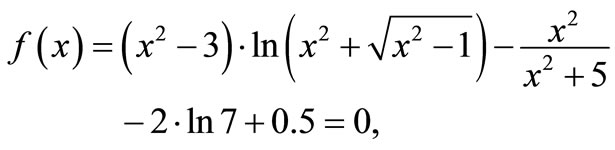
which has  as a simple root, the following Table 1 illustrates the computation by formula (8) started by x0 = 3 and x1 = 2. The correct value of the root α to 9 decimal places is 2.236067978.
as a simple root, the following Table 1 illustrates the computation by formula (8) started by x0 = 3 and x1 = 2. The correct value of the root α to 9 decimal places is 2.236067978.
Table 2 illustrates the computation by formula (6), given in [1] started by the same values x0 = 3 and x1 = 2.
5. Discussion
Example 1 shows a comparison of convergence for the
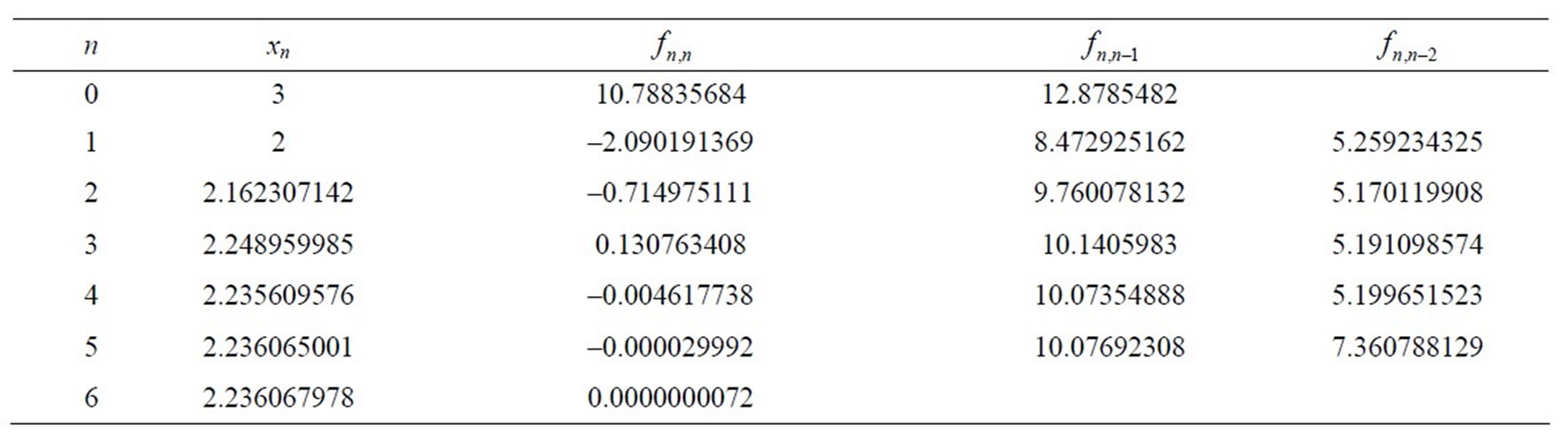
Table 1. Suggested iteration for solving .
.

Table 2. The iteration by formula (6), given in [1] for solving .
.
suggested iteration method and the iteration given by Tamara Kogan, Luba Sapir and Amir Sapir [1], the result reveals that the correct value of the root α to 9 decimal places 2.236067978 takes one step more, in addition our suggested method used only the divided differences of first and second order.
REFERENCES
- T. Kogan, L. Sapir and A. Sapir, “A Nonstationary Iterative Second-Order Method for Solving Non-Linear Equations,” Applied Mathematics and Computation, Vol. 188, No. 1, 2007, pp. 75-82. doi:10.1016/j.amc.2006.09.092
- T. I. Kogan, “Generalization of the Method of Chords for an Algebraic or Transcendental Equation,” in Russian, Tašhkent. Gos. Univ. Naun. Trudy Vyp, Vol. 276, 1966, pp. 53-55.
- D. K. R. Babajee and M. Z. Dauhoo, “An Analysis of the Properties of the Variants of Newton’s Method with Third Order Convergence,” Applied Mathematics and Computation, Vol. 183, No. 1, 2006, pp. 659-684. doi:10.1016/j.amc.2006.05.116

