Advances in Bioscience and Biotechnology
Vol.3 No.4(2012), Article ID:21871,9 pages DOI:10.4236/abb.2012.34050
Investigation of the presence of rod-shaped bacteria on food surface via elastic light scattering
![]()
1School of Mechanical Engineering, Purdue University, West Lafayette, USA
2Department of Electrical and Computer Engineering Technology, Purdue University, West Lafayette, USA
3Molecular Food Microbiology Laboratory, Department of Food Science, Purdue University, West Lafayette, USA
4School of Engineering, University of California-Merced, Merced, USA
Email: *ebae@purdue.edu
Received 5 May 2012; revised 10 June 2012; accepted 6 July 2012
Keywords: Scattering; roughness; E. coli O157; food surface; diffraction
ABSTRACT
We investigated the presence and related signal-tonoise ratio (SNR) of rod-shaped bacteria on a produce surface using elastic scattering. The theoretical noise was defined as a scattering signal from a rough produce surface while the signal was defined as a scattering signal from the increasing numbers of rod-shaped bacteria on the produce surface. In this research, we measured the surface topography of a tomato using BioAFM to provide the quantitative nature of the surface roughness which was, in turn, modeled with the discrete dipole approximation (DDA) for an accurate estimation of the background scattering signature. Then we included the DDA model of rod-shaped bacteria and calculated the combined elastic scattering signature in the upper hemispherical space with different polarizations, wavelengths, and incident angles. The total scattering cross-section (TSC) and partial scattering cross-section (PSC) were both computed on six predefined aperture locations. The results indicate that, upon proper selection of the wavelength and incident angle, it was possible to provide the minimum number of bacteria (~32) to provide a differentiable elastic scattering signal from the produce surface.
1. INTRODUCTION
Recent outbreaks from various agricultural products such as spinach, tomato, and Jalapeño remind us that the food supply system is susceptible to contaminations from pathogenic bacteria and imposes a great risk on public health. The consumption of fresh produce (fruits and vegetables) is of great concern because these are grown in open fields, where the chances of exposure to the pathogenic bacteria are many. Further, the breach in sanitary practices during processing and packaging may also increase the opportunity of bacterial contamination. In addition, the economic loss due to the recall of the foods could cost in millions of dollars to the already suffering agricultural companies from the impact of the hike of the raw material price.
Therefore, for the food and healthcare industries, the rapid identification and isolation of bacteria such as pathogenic Listeria monocytogenes and Escherichia coli in products are very important [1]. In the realm of methodologies, various techniques have been developed, including morphological, immunological, and proteomics/ genomics [2]. Genome based molecular methods have been modified to reduce time-consuming enrichment steps for bacterial detection, such as real-time PCR using molecular beacons to detect E. coli O157:H7 (>10 CFU) [3], recirculating immunomagnetic separation (RIMS) coupled with real-time PCR, and standard culture methods (0.1 CFU/g of spinach) [4]. In addition, the piezoelectric-excited millimeter-size cantilever (PEMC) sensor immobilized with an antibody has been used for detection of E. coli O157:H7 [5]. Various sensing mechanisms, including light scattering, Fourrier transformed infrared (FTIR) spectroscopy, and Raman, have been developed to detect microbes based on their morphological/structural/chemical properties directly without the need for any labeling reagents. These methodologies typically utilize lasers to generate and differentiate transmission or reflection signals from the incoming probing beams depending upon the shape, thickness, or color of the sample under testing [6-8].
Light scattering has been used for feature detection and identification in areas as diverse as the biological, astrophysical, and semiconductor industries due to its speed and accuracy. When the incoming primary wavelength and outgoing secondary wavelength are identical, this method is called elastic scattering, while if there exists a wavelength shift, it is referred to as inelastic scattering. In the elastic scattering method, angular scatter measurements have been utilized for various quantitative studies of micro-particles like bacteria in flow [9] and red blood cells [10] through the use of a scatter-model based approach. Very recently, angle-resolved back scattering has been used to identify micro colonies of such bacteria in flow, by matching their known surface textures [11], instead of their individual size, shape, or refractive indices. Bronk presented an extensive description of light-scattering experiments on rod-shaped bacteria such as E. coli [12]. However, if the morphological difference was minute or the background scattering was significant, the specificity of the overall scattering signature started to lose their uniqueness. Recently, it was shown that light scattering signatures from colonies were indeed reproducible and differentiable without applying any specific labels [13-18]. Inelastic light scattering such as Raman or SERS (surface enhanced Raman spectroscopy) is another method of interrogating microorganisms. Fluorescence is the most widely-used inelastic light scattering method in flow Cytometer and confocal microscopic measurement. The microorganism of interest inherently contained certain proteins or molecules that reacted to a specific wavelength or the researchers artificially infused the fluorophore either by tagging a molecule or via genetic engineering. Even though the incoming light was incident on the microorganism, the localized areas with the specific fluorophore would only react to the light and emit photons for detection. Historically, most of the optics-based quality control of the produce was targeted at discriminating the firmness or sugar content using single wavelength [19-22] or multi-spectral methods [23- 29] rather than directly detecting the source of the contamination. Recently, some researchers have suggested a laser induced fluorescence (LIF) measurement to detect the animal feces on an apple surface [30]; this method was still categorized as an indirect method although there was a correlation between the animal feces and the existence of pathogenic bacteria. In addition, an indirect method is known to limit the types of pathogenic bacteria that could be correlated via the LIF since they might be originating from different types of sources. In general, the signal strength of the inelastic scattering is several orders of magnitude lower than the elastic scattering; therefore, a more sophisticated and costly measurement system is actually required. In addition, their specificity of incident wavelength and certain proteins limits their applicability to broader applications. Therefore, here we have investigated the optimum selection of physical parameters to detect the presence of bacteria on the rough surface via computational electromagnetic codes. First, we selected the tomato as a representative produce example and analyzed the surface characteristics via atomic force microscopy (AFM). Based on this result we provided the micro-scale model to more accurately predict the light scattering responses of both the blank tomato and the tomato with a certain number of bacteria and also provided whether light scattering distribution was differentiable.
2. MATERIAL AND METHODS
2.1. DDSURF
To predict the light scattering characteristics from the tomato surface without any labeling, we applied the discrete dipole approximation (DDA) technique for modeling the scattering [31]. In DDA, particles were subdivided into volume elements, and the optical characteristics of each element were approximated by modeling the element as a single electric dipole. The dimensions of the volume elements represented by the dipoles must be much smaller than the wavelength of the incident light (typically < λ/10). Typically, the DDA modeled the light scattering problem in free space while a new technique was reported that modeled the scattering from particles on the surface using iterative solvers [32,33]. This code, called DDSURF, was crucial to appropriately model multiple bacteria on the tomato surface. As is shown in Figure 1, the total electrical field at any dipole was composed of the electrical field incident upon the cells and the vector sum of the electric fields incident from all other dipoles making up the neighboring cells, including the reflections off of the substrate [34,35].
When a laser source was incident upon the dipole array, the dipole moment  at dipole
at dipole  was related to the electromagnetic field shown as:
was related to the electromagnetic field shown as:
 , (1)
, (1)

Figure 1. Modeling of rod-shaped bacterial using discrete dipole approximation. Bacteria was modeled with many dipoles and placed on top of a random rough surface. The interbacteria (Edirect) and bacteria-surface (Ereflection) interactions were all included for accurate computation. The figure on the right insert shows an example of 7 bacteria on the surface (top) and their scattering pattern on the hemispherical surface.
where  was the dipole polarizability tensor and
was the dipole polarizability tensor and  was the total electric field present at the dipole. In the presence of a surface, the electric field incident on the receiving dipole also included components from the surface-reflected incident shown as:
was the total electric field present at the dipole. In the presence of a surface, the electric field incident on the receiving dipole also included components from the surface-reflected incident shown as:
 , (2)
, (2)
where  was the direct interaction at the
was the direct interaction at the  dipole and
dipole and  was the surface reflected interaction of the
was the surface reflected interaction of the  between. When we represented all N individual dipoles with Eq.2, we obtained a global
between. When we represented all N individual dipoles with Eq.2, we obtained a global  matrix equation:
matrix equation:
 (3)
(3)
where D represented a diagonal matrix from polarizability, A was a square matrix from direct interaction, R was a square matrix from reflection interaction, P was the dipole moment matrix of  , and
, and  was the incident beam matrix of
was the incident beam matrix of . After iteratively solving the scattering problem in DDSURF, a residue was defined as:
. After iteratively solving the scattering problem in DDSURF, a residue was defined as:
 , (4)
, (4)
where  was the residue at the
was the residue at the  iteration. Once the dipole moment of the all the location was computed by Eq.3, the far-field radiation pattern was computed by a summation of the scattered field radiated from each dipole as:
iteration. Once the dipole moment of the all the location was computed by Eq.3, the far-field radiation pattern was computed by a summation of the scattered field radiated from each dipole as:
 , (5)
, (5)
where indices i and j are used for the ith observation point and jth dipole center location.  and
and  are the electric fields at dipole j due to the TM and TE incident plane waves with a wavevector k = −ksca. To explore the differentiability of the light scattering pattern against the physical input parameters, we compared the reflection scattering signature of a control sample with and without bacteria on the surface and the total number of bacteria models were also varied to investigate the theoretical detection limit beyond the background scattering signal. We defined a differential scattering cross-section (DSC) as a power dissipated per unit solid angle and the DSC was formulated as [36]:
are the electric fields at dipole j due to the TM and TE incident plane waves with a wavevector k = −ksca. To explore the differentiability of the light scattering pattern against the physical input parameters, we compared the reflection scattering signature of a control sample with and without bacteria on the surface and the total number of bacteria models were also varied to investigate the theoretical detection limit beyond the background scattering signal. We defined a differential scattering cross-section (DSC) as a power dissipated per unit solid angle and the DSC was formulated as [36]:
 (6)
(6)
where Isca was the scattered irradiance, A was the detection area, r was the distance from feature to the observation point, Iinc was the incident irradiance, and W was the detection solid angle. The total scattering cross-section (TSC) was defined as the integral of the DSC over the hemispherical distribution which integrated all the differentially scattered photons on the 2π radian and was defined as the total power scattered by the incident intensity which gives the unit of area (µm2). The far-field quantities which provide the quantitative indicator were the TSC and the partial scattering cross-section (PSC), as is shown in Figure 2. However, the TSC value provided limited information regarding the spatial distribution of scattered light. Therefore, we also defined the PSC as:
 , (7)
, (7)
where Csc was the TSC, Ω was the solid angle, Is was the scattered intensity, R was the distance from the scatterer to the detector, Ii was the incident intensity, and A was the aperture area. Therefore, the SNR was defined as:
 (8)
(8)
where PSCb and PSCt were the cross-sections with and without the bacteria on the tomato’s surface.
2.2. Sample Measurement
To understand the surface scattering from bacteria on the surface of produce, it was critical to understand the surface roughness of the produce itself which played a role as a background noise in the scatter measurement (and eventually determined the Signal-to-noise ratio (SNR)). Here we performed the atomic force microscopy (AFM) measurement of a clean tomato and computed the surface statistics. The AFM was performed using the Bioscope II

Figure 2. Definition and variation of PSC in the Cartesian coordinate. P and S define the polarization of the incident light. AP1 to AP3 was when the detector was located at (θ, ϕ) of (75˚, 90˚), (75˚, 90˚), and (75˚, 90˚). For backscattering, AP4 to AP6 was located at (75˚, 0˚), (75˚, 0˚), and (75˚, 0˚). Inset shows the f/2 collection optics of PSC with f = 50 mm.
AFM and an associated controller (Veeco Instruments, Santa Barbara, CA). Surface topography measurements were conducted in air using a tapping mode and an OTESPA (Veeco) cantilever operating at 322 KHz where the scans were collected at a rate of 1 Hz. Dehydration issues were addressed by eliminating the optical microscopy light and minimizing the length of experiments. A fresh tomato was cut at approximately 1 × 1 mm and placed on the glass slide for AFM measurements. Six different samples were selected with an approximate 100 × 100 µm2 area by use of the tapping mode, and both the root-mean-square (RMS) and average roughness (Ra) were computed. The measurement results were then converted to the DDA model which incorporated all the bacteria-tomato surface interactions in a near-field scattering. When the surface roughness was smooth such as with a silicon wafer, light scattering could provide a high signal to noise ratio since the scattering from the background was negligible. As shown in the inset of Figure 1, when rod-shaped bacteria were modeled on an optically flat surface, the background scattering was negligible so that it was sufficient to measure the TSC to detect the presence of bacteria. However, to perform a similar prediction on a real-food sample, situations changed dramatically. According to Table 1, the surface roughness of the food sample was on the same order of magnitude with the bacteria itself which made it difficult to discriminate in the light scattering signature as compared to the smooth surface scattering. In addition, the light distribution was now coupled with both bacteria and background scattering which now required a careful design of the specific position of the detector to maximize the signal level. The DDSURF code enabled us to directly model the tomato sample surface and to include in the inter-bacteria and bacteria-surface interactions which provided a theoretical prediction of which combination of physical parameters would have an optimum signalto-noise ratio (SNR) with a rough surface.
Figure 3(a) displays the surface characteristics of a tomato which demonstrated diamond shaped craters. The quantitative measurement results from the AFM were then converted to a DDSURF input file, as is shown in Figure 3(b), where a cluster of four bacteria was positioned at the center of the valley. The dotted circled area of approximately 40 μm in diameter was selected and programmed to provide a 3-D input dipole model as:
 (9)
(9)

Table 1. Surface statistics of the tomator sample.

Figure 3. Surface characteristics of a tomato sample of 100 μm × 100 μm area. (a) is the 2D map of the tomato surface. The dotted-circle shows the 40 μm area while (b) shows the dipole model of the tomato surface with 4 bacterial cells on the center of the region of interest.
where Zd(xi,yi) was the height converted to the number of dipoles, n was the refractive index, D was the number of divisions per wavelength, f(xi,yi) was the height profile from the AFM, and λ was the incident wavelength.
3. RESULTS
3.1. Surface Roughness Measurement
An average six different samples provided a basic understanding on the surface roughness of a tomato surface, and their average Ra and RMS values were 0.3104 and 0.3854 µm, respectively.
3.2. Scattering Simulation
3.2.1. Variation of Physical Parameters versus the TSC
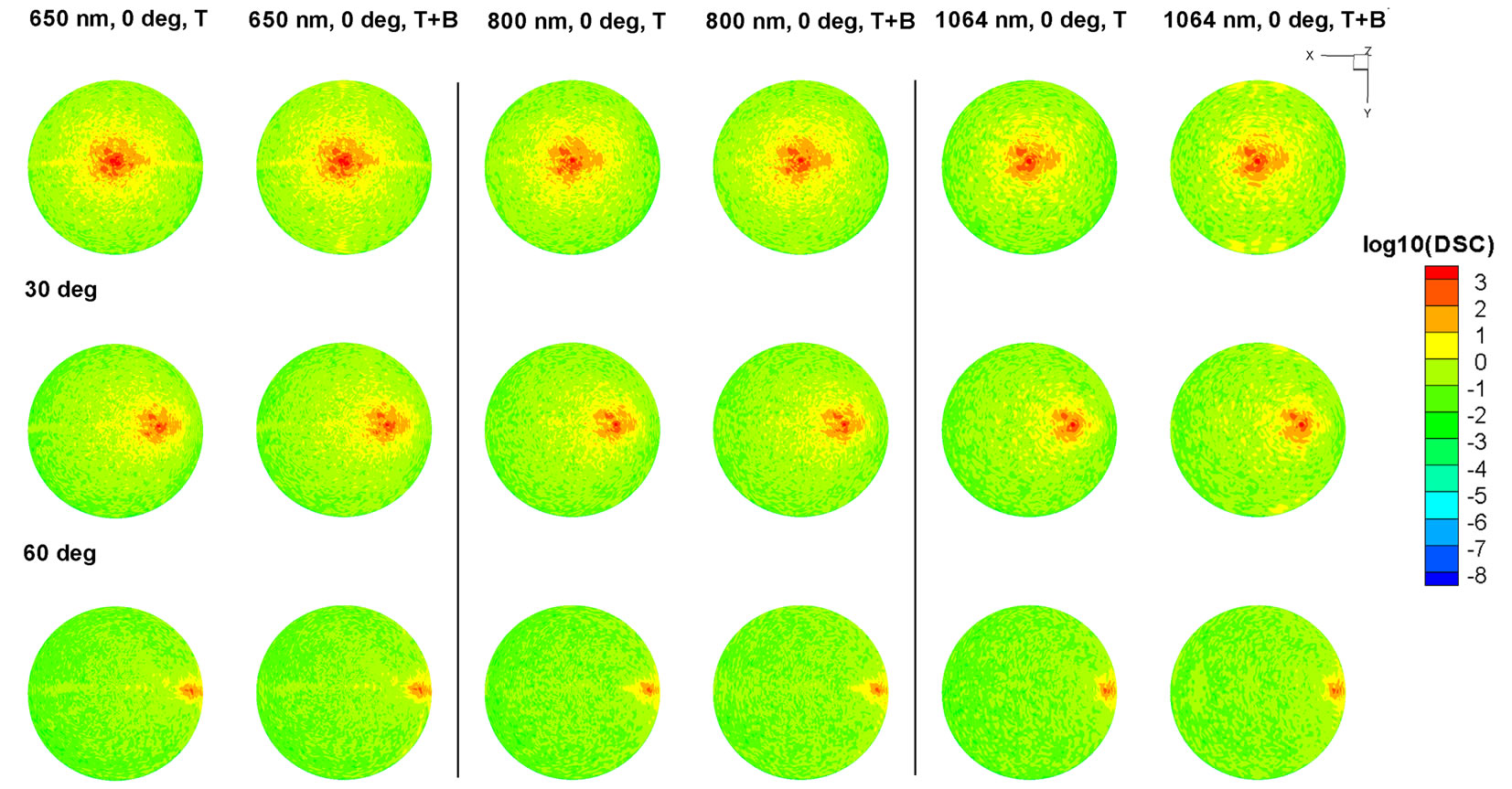
To explore the differentiability of the TSC against the physical input parameters, we compared the reflection scattering signature of a control sample with and without bacteria on the surface. We assumed that there were 8 individual bacteria sitting on the center of the valley of the tomato surface and varied the incident polarization (P & S polarization), incident angle (0˚, 30˚, 60˚), and wavelength (650 nm, 800 nm, 1064 nm). Using the DDSURF we computed the internal dipole polarizability and then computed the measurable far-field scattering quantity via the TSC and DSC as shown in Table 2.
Label T represents when only tomato model of Figure 4 was computed while the T+B represents when there were 8 bacteria on the surface. The Gaussian incident beam was assumed with a 1/e2 diameter of 40 μm beam spot size. In terms of wavelength, 650 nm generated a larger TSC at the normal incidence for both polarizations while the infrared wavelength of 1064 nm generated a larger TSC then 800 nm. When bacteria were present, most of the cases increased the TSC from 0.2% (1064 nm, P pol, 30˚) - 10.7% (1064 nm, P pol, 60˚) even though the dipole volume of the 8 bacteria contributed to only 2.3% of total number of dipoles. In designing a
 (a)
(a) (b)
(b)
Figure 4. Hemispherical light scattering patterns computed for different wavelengths (650, 800, and 1064 nm) and incident angles (0˚, 30˚, and 60˚) for (a) P and (b) S polarization incident beams.

Table 2. Spectroscopic TSC for 8 bacteria on the tomato surface.
measurement system, the hemispherical distribution of the light scattering provided valuable information regarding the strategic position of the detector to achieve an optimized SNR.
3.2.2. Number of Bacteria versus TSC & PSC
Another important aspect was the relationship of bacterial growth and the scattered power. This was important since the surface of the produce was a rough surface and the size of the bacteria was on the same order of magnitude. Here we have investigated the influence of bacterial growth to the scattering pattern. The rod-shaped bacterial dipole model was constructed starting from 1 to 32 bacteria, and the incident wavelength was set to 1064 nm which established the maximum contrast from the previous simulation. The TSC of each case for P and S polarizations was analyzed as is shown in Figure 5. The results indicated that for this wavelength, the P polarization with 60˚ of the incident angle generated the largest
 (a)
(a) (b)
(b)
Figure 5. Variation of TSC from the blank tomato surface when the number of bacteria is doubled every 30 min for (a) P and (b) S polarization.
variation of total scattered light. For the S polarization, the TSC variation was less sensitive to the increasing number of bacteria up to 32. This information has provided us with the theoretical minimum number of bacteria needed to measure a detectable difference of the TSC value which could also be correlated to the minimum required growth time for the detectability.
While the TSC provided a general idea of total light scattering compared to the background scattering, it was beneficial to analyze the PSC for a certain location of the hemispherical distribution since the real measurement system consisted of either a point detector or a finite area detector which integrated a certain solid angle of scattered light. The PSC value provided an actual signal level that we could measure with a certain design of an optical measurement system. To support this idea, we defined a coordinate system of hemispherical distribution and a six finite aperture location based on the observation of the hemispherical scattering pattern from Figure 4 where we assumed the instrument with an aperture of f/2 collection optics. As is shown in Figure 2, the cartesian coordinate system was defined with a plane of incidence on the XZ plane. Apertures 1 to 3 (AP1-AP3) denote the oblique angle forward scattering, where we have only measured for the +Y axis due to the symmetry of the scattering pattern with the φ angles of 90˚, 120˚, and 150˚. Apertures 4 to 6 (AP4-AP6) denoted the backscattering apertures. Figure 6 shows the SNR for (a) 0˚ and (b) 60˚ of the incident angle of P polarization with 1024 nm.
4. DISCUSSION
The simulation results have provided us with an interesting understanding of the scattering nature of bacteria on food surfaces. First, the P polarization was less sensitive to the background structure as the incident angle increased, a factor which played favorably in the detection of the bacteria. Since overall background noise from the tomato surface decreased as the incident angle increased, this resulted in a higher variation of relative TSC when the bacteria were present. Since P polarization was defined as a light component parallel to the plane of incidence (the XZ plane in Figure 2), it was divided by the horizontal and vertical components. As the incident angle increased, the horizontal component decreased while the vertical component increased which explained why the overall TSC decreased with the larger incident angle. Meanwhile, the S polarization was more sensitive to the background structure which generated more scattered light as the incident angle increased. Furthermore, any variation of wavelength or incident angle did not result in any significant changes in TSC when the bacteria were present. This could be explained similarly as a P polarization case. Since S polarization was defined to be perpendicular to the plane of incidence, we can observe that the horizontal component (in Y-direction) was maintained through all of the incident angles thus effectively blinding the presence of bacteria even with different incident angles and wavelengths. According to Figure 6, certain combinations of wavelength, polarizations, and incident angles resulted in a higher SNR. For example, when bacteria was shined at 1064 nm, a 0˚ scattering displays a strong side scattering at the (θ: 60˚ - 80˚, φ: 90˚ and 270˚) and 30˚ scattering shows similar peaks (θ: 60˚ - 80˚, φ: 120˚ and 240˚) which did not exist on blank tomato surface scattering. In addition, for a 60˚ incident angle, there was a backscattering signal (θ: 60˚ - 80˚, φ: 20˚ - −20˚) which was not shown at the blank tomato surface scattering and other reports of rough surface scattering [37-39]. We could observe similar phenomenon for 650 nm cases with 0˚ and 60˚ incident angles.
 (a)
(a) (b)
(b)
Figure 6. Estimation of the SNR for p polarization and (a) 0˚ incidence angle and (b) 60˚ incidence angle for an incident wavelength of 1024 nm.
The simulation results provided the theoretical SNR under the rough surface scattering which can be directly applicable to building an instrument. Figure 6(a) provided the SNR (PSCb/PSCt) for different aperture locations versus the number of bacteria for the P polarization and 0˚ incident angle. These results indicated that when we strategically positioned the detector on AP1, the SNR was maximum along all of the number of bacteria populations (SNR of 15 when N = 32) and it was approximately proportional to the number of bacteria populations. The rest of the aperture locations displayed low SNR across the bacterial population which rendered it difficult to differentiate the signal from the background noise. Figure 6(b) shows the similar results for a P polarization and 60˚ incident angle. In this case, the maximum SNR occurred at AP2 and AP6 which was the side scattering lobe and low backscattering lobe. Thus, the instrument could be designed based on this result to maximize the SNR under rough surface scattering without labeling or tagging the bacteria sample.
5. CONCLUSION
As is evidenced with this study, we have investigated the theoretical detection limits of bacteria on the food surface via elastic scattering. The tomato surface topography was accurately measured with an AFM and converted into DDSURF models which resulted in the background noise level. Then we modeled the increasing number of rod-shaped bacteria and combined the same with the tomato model to generate a comprehensive scattering signature with various physical parameters such as wavelengths, incident angles, and polarizations. For a quantitative assessment, the TSC was compared with the parameter variations and provided that the P polarization with an oblique incident angle provided the best signal variation. The PSC was defined at six detector locations, showing that 1024 nm with 60˚ incident angles can provide the SNR of 14 at a specific detector position.
6. ACKNOWLEDGEMENTS
This research was supported through a cooperative agreement with the Agricultural Research Service of the US Department of Agriculture project number 1935-42000-035 and the Center for Food Safety and Engineering at Purdue University.
REFERENCES
- Vazquez-Boland, J.A., Kuhn, M., Berche, P., Chakraborty, T., Dominguez-Bernal, G., Goebel, W., Gonzalez-Zorn, B., Wehland, J. and Kreft, J. (2001) Listeria pathogenesis and molecular virulence determinants. Clinical Microbiology Reviews, 14, 584-640. doi:10.1128/CMR.14.3.584-640.2001
- Bhunia, A.K., Nanduri, V., Bae E. and Hirleman, E.D. (2009) Biosensors, foodborne pathogen detection. In: Flickinger, M.C., Ed., Encyclopedia of Industrial Biotechnology: Bioprocess, Bioseparation, and Cell Technology, John Wiley & Sons, Hoboken.
- Sandhya, S., Chen, W. and Mulchandani, A. (2008) Molecular beacons: A real-time polymerase chain reaction assay for detecting Escherichia coli from fresh produce and water. Analytica Chimica Acta, 614, 208-212. doi:10.1016/j.aca.2008.03.026
- Himathongkham, S., Dodd, M.L., Yee, J.K., Lau, D.K., Bryant, R.G., Badoiu, A.S., Lau, H.K., Guthertz, L.S., Crawford-Miksza, L. and Soliman, M.A. (2007) Recirculating immunomagnetic separation and optimal enrichment conditions for enhanced detection and recovery of low levels of Escherichia coli O157:H7 from fresh leafy produce and surface water. Journal of Food Protection, 70, 2717-2724.
- Maraldo, D. and Mutharasan, R.A.J. (2007) Preparationfree method for detecting Escherichia coli O157:H7 in the presence of spinach, spring lettuce mix, and ground beef particulates. Journal of Food Protection, 70, 2651- 2655.
- Barton, J., Hirst, E., Kaye, P., Saunders, S. and Clark, D. (1999) Airborne particle characterization by spatial scattering and fluorescence. Air Monitoring and Detection of Chemical and Biological Agents Ii, 3855, 92-100.
- Bronk, B.V., Li, Z.Z. and Czege, J. (2001) Polarized light scattering as a rapid and sensitive assay for metal toxicity to bacteria. Journal of Applied Toxicology, 21, 107-113. doi:10.1002/jat.730
- Holler, S., Pan, Y.L., Chang, R.K., Bottiger, J.R., Hill, S.C. and Hillis, D.B. (1998) Two-dimensional angular optical scattering for the characterization of airborne microparticles. Optics Letters, 23, 1489-1491. doi:10.1364/OL.23.001489
- Shvalov, A.N., Soini, J.T., Surovtsev, I.V., Kochneva, G.V., Sivolobova, G.F., Petrov, A.K. and Maltsev, V.P. (2000) Individual Escherichia coli cells studied from light scattering with the scanning flow cytometer. Cytometry, 41, 41-45. doi:10.1002/1097-0320(20000901)41:1<41::AID-CYTO6>3.0.CO;2-N
- Shvalov, A.N., Surovtsev, I.V., Chernyshev, A.V., Soini, J.T. and Maltsev, V.P. (1999) Particle classification from light scattering with the scanning flow cytometer. Cytometry, 37, 215-220. doi:10.1002/(SICI)1097-0320(19991101)37:3<215::AID-CYTO8>3.0.CO;2-3
- Pan, Y.L., Holler, S., Chang, R.K., Hill, S.C., Pinnick, R.G., Niles, S., Bottiger, J.R. and Bronk, B.V. (1999) Real-time detection and characterization of individual flowing airborne biological particles: Fluorescence spectra and elastic scattering measurements. Air Monitoring and Detection of Chemical and Biological Agents Ii, 3855, 117-125.
- Bronk, B.V., Druger, S.D., Czege, J. and Vandemerwe, W.P. (1995) Measuring diameters of rod-shaped bacteria in-vivo with polarized-light scattering. Biophysical Journal, 69, 1170-1177. doi:10.1016/S0006-3495(95)79991-X
- Bae, E., Aroonnual, A., Bhunia, A.K. and Hirleman, E.D. (2011) On the sensitivity of forward scattering patterns from bacterial colonies to media composition. Journal of Biophotonics, 4, 236-243. doi:10.1002/jbio.201000051
- Bae, E., Banada, P.P., Huff, K., Bhunia, A.K., Robinson, J.P. and Hirleman, E.D. (2008) Analysis of time-resolved scattering from macroscale bacterial colonies. Journal of Biomedical Optics, 13, Article ID: 014010.
- Bae, E., Aroonnual, A., Bhunia, A.K., Robinson, J.P. and Hirleman, E.D. (2009) System automation for a bacterial colony detection and identification instrument via forward scattering. Measurement Science & Technology, 20, Article ID: 20015802. doi:10.1088/0957-0233/20/1/015802
- Banada, P.P., Huff, K., Bae, E., Rajwa, B., Aroonnual, A., Bayraktar, B., Adil, A., Robinson, J.P., Hirleman, E.D. and Bhunia, A.K. (2009) Label-free detection of multiple bacterial pathogens using light-scattering sensor. Biosensors & Bioelectronics, 24, 1685-1692. doi:10.1016/j.bios.2008.08.053
- Bae, E., Bai, N., Aroonnual, A., Bhunia, A.K. and Hirleman, E.D. (2010) Label-free identification of bacterial microcolonies via elastic scattering. Biotechnology and Bioengineering, 108, 637-644. doi:10.1002/bit.22980
- Bae, E., Bai, N., Aroonnual, A., Robinson, J.P., Bhunia, A.K. and Hirleman, E.D. (2010) Modeling light propagation through bacterial colonies and its correlation with forward scattering patterns. Journal of Biomedical Optics, 15, Article ID: 045001. doi:10.1117/1.3463003
- Cho, Y.J. and Han, Y.J. (1999) Nondestructive characterization of apple firmness by quantitation of laser scatter. Journal of Texture Studies, 30, 625-638. doi:10.1111/j.1745-4603.1999.tb00234.x
- De Belie, N., Tu, K., Jancsok, P. and De Baerdemaeker, J. (1999) Preliminary study on the influence of turgor pressure on body reflectance of red laser light as a ripeness indicator for apples. Postharvest Biology and Technology, 16, 279-284. doi:10.1016/S0925-5214(99)00025-3
- Sotome, I., Hryniewicz, M., Anthonis, J., Ramon, H. and De Baerdemaeker, J. (2005) Laser scattering and surface model in fruit quality research. Proceedings of the 3rd International Symposium on Applications of Modelling as an Innovative Technology in the Agri-Food-Chain, Leuven, 29 May-2 June 2005, 605-611.
- Xing, J., Ngadi, M., Wang, N. and De Baerdemaeker, J. (2006) Bruise detection on tomatoes based on the light scattering image. American Society of Agricultural and Biological Engineers Annual International Meeting, Portland, 9-12 July 2006, Article ID: 066185.
- Lu, R. (2001) Predicting firmness and sugar content of sweet cherries using near-infrared diffuse reflectance spectroscopy. Transactions of the ASAE, 44, 1265-1271.
- Hahn, F. (2002) Multi-spectral prediction of unripe tomatoes. Biosystems Engineering, 81, 147-155. doi:10.1006/bioe.2001.0035
- Lu, R. and Ariana, D. (2002) A near-infrared sensing technique for measuring internal quality of apple fruit. Applied Engineering in Agriculture, 18, 585-590.
- Polder, G., van der Heijden, G. and Young, I.T. (2002) Spectral image analysis for measuring ripeness of tomatoes. Transactions of the ASAE, 45, 1155-1161.
- Lu, R. (2003) Detection of bruises on apples using nearinfrared hyperspectral imaging. Transactions of the ASAE, 46, 523-530.
- Mehl, P.M., Chen, Y.R., Kim, M.S. and Chan, D.E. (2004) Development of hyperspectral imaging technique for the detection of apple surface defects and contaminations. Journal of Food Engineering, 61, 67-81. doi:10.1016/S0260-8774(03)00188-2
- Xing, J. and De Baerdemaeker, J. (2005) Bruise detection on “Jonagold” apples using hyperspectral imaging. Postharvest Biology and Technology, 37, 152-162. doi:10.1016/j.postharvbio.2005.02.015
- Kim, M.S., Cho, B.K., Lefcourt, A.M., Chen, Y.R. and Kang, S. (2008) Multispectral fluorescence lifetime imaging of feces-contaminated apples by time-resolved laser-induced fluorescence imaging system with tunable excitation wavelengths. Applied Optics, 47, 1608-1616. doi:10.1364/AO.47.001608
- Purcell, E.M. and Pennypac, Cr. (1973) Scattering and absorption of light by nonspherical dielectric grains. Astrophysical Journal, 186, 705-714.
- Schmehl, R., Nebeker, B.M. and Hirleman, E.D. (1997) Discrete-dipole approximation for scattering by features on surfaces by means of a two-dimensional fast Fourier transform technique. Journal of the Optical Society of America A: Optics Image Science and Vision, 14, 3026- 3036.
- Nebeker, B.M., Starr, G.W. and Hirleman, E.D. (1998) Evaluation of iteration methods used when modeling scattering from features on surfaces using the discrete-dipole approximation. Journal of Quantitative Spectroscopy & Radiative Transfer, 60, 493-500. doi:10.1016/S0022-4073(98)00023-5
- Bae, E. and Hirleman, E.D. (2007) Extending the applicability of the discrete dipole approximation for multiscale features on surface. Journal of Quantitative Spectroscopy & Radiative Transfer, 107, 470-478. doi:10.1016/j.jqsrt.2007.03.001
- Bae, E. and Hirleman, E.D. (2009) Computational analysis and diagonal preconditioning for the discrete dipole approximation on surface. Journal of Quantitative Spectroscopy & Radiative Transfer, 110, 51-61. doi:10.1016/j.jqsrt.2008.10.001
- Bohren, C.F. and Hoffman, D.R. (1998) Absorption and scattering of light by small particles. A Wiley-Interscience Publication, New York.
- Odonnell, K.A. and Knotts, M.E. (1991) Polarization dependence of scattering from one-dimensional rough surfaces. Journal of the Optical Society of America A: Optics Image Science and Vision, 8, 1126-1131.
- Ruiz-Cortes, V.A. and Dainty, J.C. (2002) Experimental light-scattering measurements from large-scale composite randomly rough surfaces. Journal of the Optical Society of America A: Optics Image Science and Vision, 19, 2043- 2052.
- Tahir, K. and Dainty, C. (2005) Experimental measurements of light scattering from samples with specified optical properties. Journal of Optics A: Pure and Applied Optics, 7, 207-214. doi:10.1088/1464-4258/7/5/001
NOTES
*Corresponding author.

