ABSTRACT

For characterization of negative exponential distribution one needs any arbitrary non-constant function only in place of approaches such as identical distributions, absolute continuity, constant regression of order statistics, continuity and linear regression of order statistics, non-degeneracy etc. available in the literature. Path breaking different approach for characterization of negative exponential distribution through expectation of non-constant function of random variable is obtained. An example is given for illustrative purpose.

1. Introduction

Knowing characterizing property may provide unexpectedly accurate information about distributions and one can recognize a class of distributions before any statistical inference is made. This feature of characterization of probability distributions is peculiar to characterizing property and attracted attention of both theoretician and applied workers but there is no general theory of it.

Various approaches were used for characterization of negative exponential distribution. Among many other people, Fisz [1], Tanis [2], Rogers [3] and Fergusion [4] used properties of identical distributions, absolute continuity, constant regression of adjacent order statistics, linear regression of adjacent order statistics of random variables and characterized negative exponential distribution. Using independent and non-degenerate random variables Fergusion ([5,6]) and Crawford [7] characterized negative exponential distribution. Linear regression of two adjacent record values used by Nagaraja ([8,9],) were different from two conditional expectations, conditioned on a non-adjacent order statistics used by Khan [10] to characterize negative exponential distribution.

 

In this research note section 2 is devoted for characterization based on identity of distribution and equality of expectation function randomly variable for a negative exponential distribution with probability density function (pdf).

(1.1)

where are known as constants, is positive absolute continuous function and is everywhere differentiable function. Since derivative of is positive, the range is truncated by from left.

2. Characterization

Theorem 2.1 Let be a random variable with distribution function. Assume thatis continuous on the interval, where. Let and 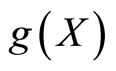be two distinct differentiable and intregrable functions of X on the interval where and moreover be non constant. Then

(2.1)

is the necessary and sufficient condition for pdf of to be defined in (1.1).

Proof Given defined in (1.1), for necessity of (2.1) if is such that where is differentiable function then

(2.2)

Differentiating with respect to on both sides of (2.2), replacing for and simplifying one gets

(2.3)

which establishes necessity of (2.1). Conversely given (2.1), let be such that

(2.4)

which can be rewritten as

(2.5)

which reduces to

(2.6)

Hence

. (2.7)

Since is increasing integrable and differentiable function on the interval with the following identity holds

. (2.8)

Differentiating with respect toand simplifying (2.8) after taking as one factor, (2.8) reduces to

, (2.9)

where is a function of only derived in (2.3) and is a function of and only derived in (2.7).

Since be increasing integrable and differentiable function on the interval where and since is positive intregrable function on the interval where with and integrating (2.7) over the interval on both sides, one gets (2.7) as

(2.10)

and

.

Substituting in derived in (2.10), reduces to defined in (1.1) which establishes sufficiency of (2.1).

Remark 2.1 Using derived in (2.3), the given in (1.1) can be determined by

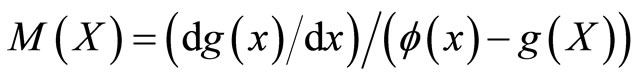(2.11)

and pdf is given by

(2.12)

where is decreasing function for with such that it satisfies

. (2.13)

Illustrative Example: Using method described in the remark characterization of negative exponential distribution through survival function is illustrated.

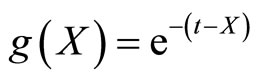
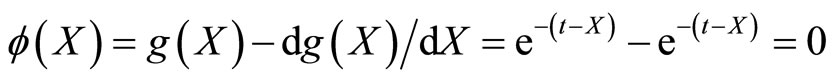
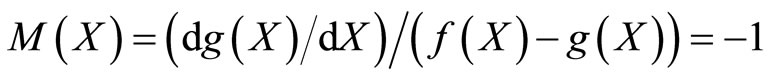
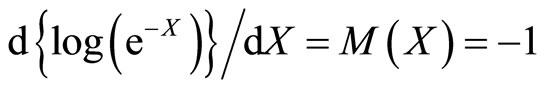
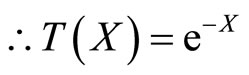
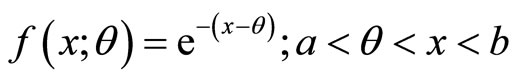
3. Conclusion

To characterize pdf defined in (1.1) one needs any arbitrary non-constant function of which should only be differentiable and integrable.

REFERENCES

NOTES

^*This work is supported by UGC Major Research Project No: F.No.42-39/2013(SR), dated 12-3-2013.