Paper Menu >>
Journal Menu >>
 J. Software Engineering & Applications, 2009, 2: 301-307 doi:10.4236/jsea.2009.24039 Published Online November 2009 (http://www.SciRP.org/journal/jsea) Copyright © 2009 SciRes JSEA 301 A Hybrid Importance Sampling Algorithm for Estimating VaR under the Jump Diffusion Model Tian-Shyr Dai1; Li-Min Liu2 1Department of Information and Financial Management, Institute of Information Management and Institute of Finance, National Chiao-Tung University, Taiwan ,China; 2Department of Applied Mathematics, Chung Yuan Christian University, Taiwan, China. Email: d88006@csie.ntu.edu.tw Received July 20th, 2009; revised August 12th, 2009; accepted August 14th, 2009. ABSTRACT Value at Risk (VaR) is an important tool for estimating the risk of a financial portfolio under significant loss. Although Monte Carlo simulation is a powerful tool for estimating VaR, it is quite inefficient since the event of significant loss is usually rare. Previous studies suggest that the performance of the Monte Carlo simulation can be improved by impor- tance sampling if the market returns follow the normality or the distributions. The first contribution of our paper is to extend the importance sampling method for dealing with jump-diffusion market returns, which can more precisely model the phenomenon of high peaks, heavy tails, and jumps of market returns mentioned in numerous empirical study papers. This paper also points out that for portfolios of which the huge loss is triggered by significantly distinct events, naively applying importance sampling method can result in poor performance. The second contribution of our paper is to develop the hybrid importance sampling method for the aforementioned problem. Our method decomposes a Monte Carlo simulation into sub simulations, and each sub simulation focuses only on one huge loss event. Thus the perform- ance for each sub simulation is improved by importance sampling method, and overall performance is optimized by determining the allotment of samples to each sub simulation by Lagrange’s multiplier. Numerical experiments are given to verify the superiority of our method. Keywords: Hybrid Importance Sampling, VaR, Straddle Options, Jump Diffusion Process 1. Introduction Value at Risk (VaR) is an important tool for quantifying and managing portfolio risk. It provides a way of meas- uring the total risk to which the financial institution is exposed. VaR denotes a loss that will not be ex- ceeded at certain confidence level 1−p over a time hori- zon from t to. To be more specific, tt () tt t PV Vp , where V denotes portfolio value at time . Typically, p is close to zero. For convenience, we define tt t VV and as the portfolio gain and the return over the time span Some academic papers focus on a relevant problem: computes the probability p of a portfo- lio loss to exceed a given level [], and our paper will focus on this problem. ( tt ) t t VV/V 1 t. VaR can not be evaluated by simple yet exact analyti- cal formulas when the assumptions on the processes of the assets’ values or the composition of financial portfo- lios are complex [2]. The asset in this paper is assumed to be stock for convenience. The Monte Carlo simulation is a flexible and powerful tool to estimate VaR since it is usually more easily to sample the stock prices from com- plex diffusion price processes than to estimate the distri- butions of the stock prices at a certain time point. We can repeatedly evaluate possible future values of a financial portfolio by sampling prices of stocks that compose the portfolio and the distribution of the portfolio gain can then be estimated. However, estimating VaR by the Monte Carlo simulation is very inefficient since the event that the portfolio loss exceeds is rare (note that p is close to zero) and a large number of samples is thus re- quired to obtain an accurate probability estimate of this rare event. By assuming the market returns follow nor- mal distributions, Glasserman et al. develop an efficient variance reduction method based on importance sam- pling that can drastically reduce the number of samples required to achieve accurate probabilities estimates of rare events [3]. In their method, the stock prices are sam- pled from a new probability measure where the event of significant loss is more likely to happen than in the original one. This new probability measure is selected to 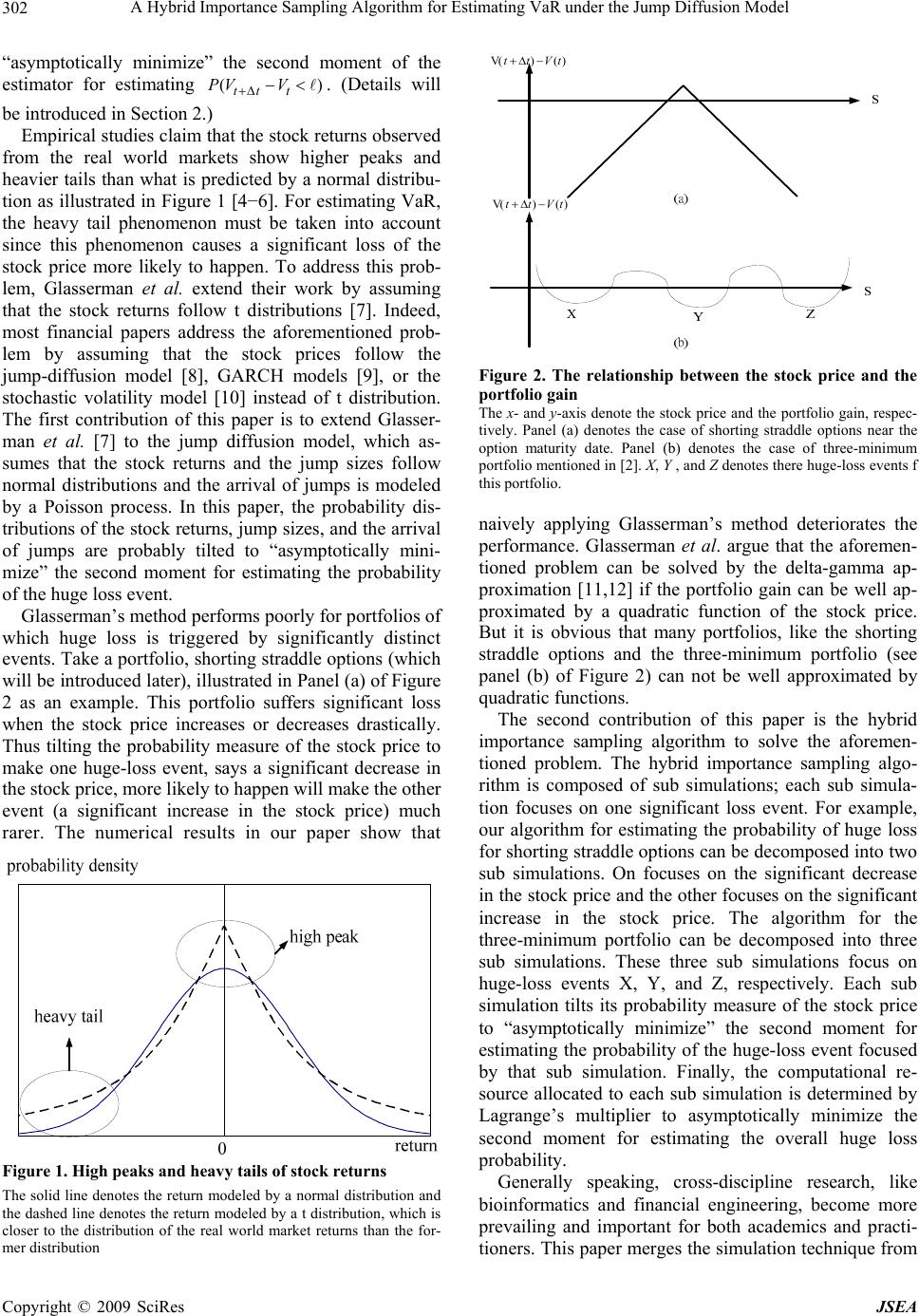 A Hybrid Importance Sampling Algorithm for Estimating VaR under the Jump Diffusion Model 302 “asymptotically minimize” the second moment of the estimator for estimating . (Details will be introduced in Section 2.) ( tt t PV V ) Empirical studies claim that the stock returns observed from the real world markets show higher peaks and heavier tails than what is predicted by a normal distribu- tion as illustrated in Figure 1 [4−6]. For estimating VaR, the heavy tail phenomenon must be taken into account since this phenomenon causes a significant loss of the stock price more likely to happen. To address this prob- lem, Glasserman et al. extend their work by assuming that the stock returns follow t distributions [7]. Indeed, most financial papers address the aforementioned prob- lem by assuming that the stock prices follow the jump-diffusion model [8], GARCH models [9], or the stochastic volatility model [10] instead of t distribution. The first contribution of this paper is to extend Glasser- man et al. [7] to the jump diffusion model, which as- sumes that the stock returns and the jump sizes follow normal distributions and the arrival of jumps is modeled by a Poisson process. In this paper, the probability dis- tributions of the stock returns, jump sizes, and the arrival of jumps are probably tilted to “asymptotically mini- mize” the second moment for estimating the probability of the huge loss event. Glasserman’s method performs poorly for portfolios of which huge loss is triggered by significantly distinct events. Take a portfolio, shorting straddle options (which will be introduced later), illustrated in Panel (a) of Figure 2 as an example. This portfolio suffers significant loss when the stock price increases or decreases drastically. Thus tilting the probability measure of the stock price to make one huge-loss event, says a significant decrease in the stock price, more likely to happen will make the other event (a significant increase in the stock price) much rarer. The numerical results in our paper show that Figure 1. High peaks and heavy tails of stock returns The solid line denotes the return modeled by a normal distribution and the dashed line denotes the return modeled by a t distribution, which is closer to the distribution of the real world market returns than the for- mer distribution )()V( tVtt )()V( tVtt Figure 2. The relationship between the stock price and the portfolio gain The x- and y-axis denote the stock price and the portfolio gain, respec- tively. Panel (a) denotes the case of shorting straddle options near the option maturity date. Panel (b) denotes the case of three-minimum portfolio mentioned in [2]. X, Y , and Z denotes there huge-loss events f this portfolio. naively applying Glasserman’s method deteriorates the performance. Glasserman et al. argue that the aforemen- tioned problem can be solved by the delta-gamma ap- proximation [11,12] if the portfolio gain can be well ap- proximated by a quadratic function of the stock price. But it is obvious that many portfolios, like the shorting straddle options and the three-minimum portfolio (see panel (b) of Figure 2) can not be well approximated by quadratic functions. The second contribution of this paper is the hybrid importance sampling algorithm to solve the aforemen- tioned problem. The hybrid importance sampling algo- rithm is composed of sub simulations; each sub simula- tion focuses on one significant loss event. For example, our algorithm for estimating the probability of huge loss for shorting straddle options can be decomposed into two sub simulations. On focuses on the significant decrease in the stock price and the other focuses on the significant increase in the stock price. The algorithm for the three-minimum portfolio can be decomposed into three sub simulations. These three sub simulations focus on huge-loss events X, Y, and Z, respectively. Each sub simulation tilts its probability measure of the stock price to “asymptotically minimize” the second moment for estimating the probability of the huge-loss event focused by that sub simulation. Finally, the computational re- source allocated to each sub simulation is determined by Lagrange’s multiplier to asymptotically minimize the second moment for estimating the overall huge loss probability. Generally speaking, cross-discipline research, like bioinformatics and financial engineering, become more prevailing and important for both academics and practi- tioners. This paper merges the simulation technique from Copyright © 2009 SciRes JSEA  A Hybrid Importance Sampling Algorithm for Estimating VaR under the Jump Diffusion Model 303 applied mathematics and algorithm design and perform- ance comparisons knowhow from computer science dis- cipline to develop efficient numerical programs to solve finance problem. It plays a great platform to interchange the ideas, the challenges, and the techniques among the computer scientists, mathematicians, and financial ex- perts. The paper is organized as follows. The assumptions of the Merton’s jump diffusion model, the Glasserman’s importance sampling method, and the definitions of straddle options are introduced in Section 2. In Section 3, we will use shorting straddle options as an example to demonstrate how the probabilities of the jump diffusion process are tilted for each sub simulation and how the number of samples is allocated to each sub simulation to optimize the overall performance. Numerical results in Section 4 verify the superiority of our method. Section 5 concludes the paper. 2. Preliminaries 2.1 The Stock Price Process Define St as the stock price at year t. Under the Merton’s jump diffusion model, the stock price process can be expressed as (1) X t t t dS dtdW edN S t (1) where is the standard Wiener process, μ is the aver- age stock return per annum, σ is the annual volatility, X is a normal random variable that models the jump size, and t W t N denotes the Poisson process. We further assume that 2 ,)~(XN and (1) t PdN dt t . Define the stock return over the time horizonas follows: 1 , t N tt t t ti SS rttZ S i Z (2) where ~0,1ZN , t N denotes the number of jumps be- tween time t and , tt 2 ~(,) i ZN . Note that the aforementioned model degenerates into the Black- Scho- les lognormal diffusion process [13] when λ = 0 (i.e. in Equation (2)). 0 t N 2.2 Glasserman’s Importance Sampling Method This subsection sketches Glasserman’s importance sam- pling method [3] by assuming that the stock price process follows the log-normal diffusion process. Consider a portfolio which is composed of a stock. Let A denotes the event that the portfolio gain is less than: ()() 0 S()-S() =0 () () =0 (3) () =-0 ( t tp ASt tSt ttt St St rSt rr 4) =Z: f(Z)-0 (5) tp p rrttZr where we substitute Equation (2) into Equation (3) and (5), andp t rS into Equation (4). To minimize the second moment for estimating the probability of event A, Glasserman samples Z from a new probability measure instead of the original prob- ability measure (where ~0,1ZN ). The likelihood ratio for these two probabilities measures is exp()() , dfZ d (6) where Ψ(θ) ≡ logE [exp (θf(Z))]. Define E as the expected value measured under and :( )0, p AZfZttZr where ~(,1) Z Nt . Then we have *9(1 )1exp(()()) . AA dpE EfZ The second moment of the estimator is then Second moment 1exp( 2()2( ))exp(2()). A EfZ (7) To asymptotically optimize the performance of the Monte Carlo simulation, a proper θ is selected to mini- mize exp (2Ψ(θ)) by the following equation: '() 0 (8) is then determined by substituting θ (obtained from Equation (8)) into Equation (6). 2.3 Straddle Options Stock options are derivative securities that give their buyer the right, but not the obligation, to buy or sell the underlying stocks for a contractual price called the exer- cise price K at maturity. Assume that the options mature at timett then the payoffs of a call option and a put option at maturity are maxand max ,0 tt SK KS,0 tt, respectively. Shorting straddle options denotes a portfolio that shortsunits call options and 1 D Copyright © 2009 SciRes JSEA  A Hybrid Importance Sampling Algorithm for Estimating VaR under the Jump Diffusion Model Copyright © 2009 SciRes JSEA 304 2 D units put options with the same strike price. To be more specific, the portfolio gain at maturity is 12 max,0 max,0 tt tt DSKD KS . The portfo- lio gain is interpreted in terms of stock returndefined Equation (2) in Figure 3. Note that t r * 0t t K S rS (9) The portfolio gain can be expressed as follows: Portfolio Gain(10) ** 02010 * 2t (), , , tt t tt rSrrSifr rSifr * 0 , 1 t r r where 1 D and 2 D2 t r . The portfolio gain is less than if the stock returnis larger thanor lower than , where * 1 r * 2 r ** *0201 1 1 tt t rS rS rS and * 2 2 . t rS t 3. Contributions We will use shorting straddle options as an example to illustrate the major contributions of this paper. First, the huge loss events of this portfolio are identified. The Monte Carlo simulation is then decomposed into two sub simulations; each focuses on one huge loss event. Next, the probability distribution for each sub simulation is tilted to asymptotically minimize the second moment of the estimator under the jump diffusion assumption. Fi- nally, the allotment of samples for each sub simulation is determined by Lagrange’s multiplier to optimize the overall performance. 3.1 Identify the Huge Loss Events In Figure 3, the portfolio gain of shorting straddle op- tions is less than when the stock return exceeds threshold or is below r * 1 r * 2 r. For convenience, events1 A and 2 A are used to denote the events * 1t rr and * 2 r t r, respectively, as follows: ** 1102 01 :()( ) tt t Arfr rrrr * 0, , (11) * 22 2 :()0 ttt Arfrr r where and formula */t rS1() t f rand 2() t f rare derived from Equation (10). Since1 A and 2 A are mutually exclusive, the probability that the portfolio gain is less than is 1 121 2 11 AAAA pEE E . The Monte Carlo simulation for estimating p can be decomposed into two sub simulations; one focuses on event 1 A , and the other one focuses on event2 A . 3.2 Importance Sampling under the Jump Diffusion Assumption Next, we will describe how to efficiently estimate1 1 A E and 2 1A E by importance sampling. Assume that the sub simulations for estimatingand tilt their probabilities from 1 1A E 2 1A E to 1 and2 , respectively. Then 1 and 2 are derived as follows: Define 11 () log 11 ( t e ))Efrxp( )) t fr and . 22 (22 ( )) t fr ) logexp(E 11 exp( (E can be calculated as follows: ** 1110210 1 *** 102101111 exp(())exp(()) = exp(-)(exp()). tt t EfrE rrrr rrrE r * Note that 11 11 1 (exp())exp( ()) t N ti i ErE ttZZ 222 111 111 1 exp(0.5)exp()' Nt i i ttE Z 11 11 10 1 222 1111 0 222 111 1 0 exp( )exp( ) ! =exp(0.5 ! ( exp(0.5)) =! t t t t Nnn t ii in i n t n n t n e EZ EZ n enn n e n 222 1111 0.5 t =exp(), t e where tt . Thus 1 can be obtained by numerically solving the equation ' 11 () 0 (see Equation (8)) as follows: '*** 22 1102 01111 22 222 11111 11 () ()exp(0.5)0. t rrrt t Similarly, it can be derived that 222 2222 22 22222 2 0.5 * 2 exp(())exp(0.5 ). t tt Efrt t re 2 2 can also be solved numerically by the equation ' 22 ()0 as follows:  A Hybrid Importance Sampling Algorithm for Estimating VaR under the Jump Diffusion Model 305 )()V( tVtt t r 2 slope t S 1 slope t S * 0 r * 2 r * 1 r Figure 3. Shorting straddle options The x- and y-axis denote the stock return and the portfolio gain, respectively. 222 2222 '22 22 222 0.5 22 22 2 () () t tt r e * 0. Finally, the new probability distribution1 sampled by the first sub simulation can be derived by Equation (6) as follows: 1 2 1 22 222 0.5 211 222 11 111 1 11 111 1 () /2 2111 1 2 0 0.5 2 2 exp(( )()) 11 = exp ! 22 11 = ! 22 n kK t t t nZ n Zt t n n e Zt t dd fr e eefr n ee en 2 2 111 2 2 0 . n kK Z n n e That is, the first sub simulation tilts the probability from to 1 , where the distributions of random vari- ables defined in Equation (2) are changed as follows: 11 ~,1 Z Nt 222 111 1 0.5 ~ tt NPoissone and 22 11 ~ i ZN 11111 11 11exp At EEA fr . Thus 1 1A E is estimated by sampling the unbiased es- timator 111 1 xp At fr 1 1e from1 in the first , . Note that sub simulation. Similarly, the probability distribution 2 used by the second sub simulation can be derived as 2 222 2 0.5 222 2 222 22 122 2222 22 2 222 2 0.5 2 2 2 0 exp 11 =. ! 22 n tKK t eZ n Zt t n dd fr ee ee n Copyright © 2009 SciRes JSEA  A Hybrid Importance Sampling Algorithm for Estimating VaR under the Jump Diffusion Model 306 Note also that 22 2222 2 11exp AA t EE fr . The second sub simulation estimatesby sam- pling the unbiased estimator 2 1A E 22 2 1exp At 22 fr from 2 . 3.3 Allocation of Computational Resources to Each Sub Simulation Finally, we try to minimize the upper bound of the sec- ond moment for estimating p given a constraint on com- putational resources. The number of stock return samples serves as a proxy of computational resources. Assume that we can only sample N stock returns, and the num- bers of stock returns sampled in the first and the second simulations are n1 and n2, respectively. By Equation (7), the upper bounds of the second moment of the estima- tor 1111 1 1exp At fr and 2222 2 1exp At fr 1 under the probability measure 2 and are 11 p 2ex and 22 exp 2, respectively. The second moment for estimating p is then 112 2 22 exp22 exp nn (14) To minimize Equation (14) under the constraint , n1 and n2 can be solved by Lagrange multi- plier as follows: 12 Nnn 11 1 112 2 exp 2 N exp 2exp2 n (15) 22 2 11 exp 2 2 2 N exp 2exp2 n (16) 4. Numerical Results Table 1 illustrates how the probability tilting mechanism proposed in this paper greatly improves the performance of the Monte Carlo simulation. Consider a portfolio which is composed of a stock. The probability that the portfolio loses more than 5% in 0.008 year is estimated with three different approaches: Original denotes the naive Monte Carlo simulation that samples the stock re- turn from Equation (2). Lognormal denotes Glasserman et al. importance sampling method under the Black- Scholes lognormal diffusion assumption (see subsection 2.2). Jump diffusion denotes the importance sampling method derived in Equation (13). We do 100 estimations Table 1. Estimating the huge loss probability under differ- ent probability measures Probability Measure Original Lognormal Jump Dif- fusion p 0.0336 0.0339 0.0338 Var( p ) 6 2.49 10 6 1.21 10 7 3.69 10 The stock price is assumed to follow Merton’s jump diffusion process: The stock average annual return μ is 0.05, the annual volatility of the stock price σ is 0.3, the time span Δt is 0.008 year, the jump frequency λ is 6, the average jump size η is 0, and the standard derivation of jump size δ is 0.03. p and Varp denote the estimated probability and the variance, respectively. for each Monte Carlo simulation method and each esti- mation samples 10000 stock returns. The probability for the portfolio to lose more than 5% is about 3.38%. Ob- viously, the method proposed in this paper reduces the variance at a ratio of 7 6 3.69 101/7 2.49 10 , which is better than the Glasserman’s method 6 6 1.21 101/ 2 2.49 10 . Now we proceed to verify the superiority of the hybrid importance sampling algorithm in Table 2 and 3, where the stock price processes are assumed to follow the log- normal diffusion process and the Merton’s jump diffu- sion process, respectively. The first column in these two tables denotes the probability measure of the stock return sampled by each Monte Carlo simulation method, where denotes the original probability measure defined in Equation (2), 1 denotes the probability measure de- fined in Equation (12), and 2 denotes the probability measure defined in Equation (13). Hybrid denotes the hybrid importance sampling algorithm that is composed of two sub simulations, which sample stock returns from 1 and 2 , respectively. The numbers of samples allocated to these two sub simulations are determined in Equation (15) and (16), respectively. The second column p denotes the estimated probability for each Monte Carlo simulation, and the third column Var p denotes the variance of the estimated probability for each Monte Carlo simulation. We first focus on Table 2. The event that the portfolio loss exceeds is about 0.0349. This event can be de- composed into two mutually exclusive events A1 and A2 (see Equation (11)). The event A 1 (with probability 10.0049PA ) is less likely to happen than the event A2 (with probability 20.0299PA ). Although tilting the probability measure of the stock return from to 1 makes the Monte Carlo simulation estimate 1 PA more efficiently and accurately, it also damages the accuracy Copyright © 2009 SciRes JSEA  A Hybrid Importance Sampling Algorithm for Estimating VaR under the Jump Diffusion Model Copyright © 2009 SciRes JSEA 307 for estimating. It can be observed that this tilting produce inaccurate probability estimation (0.0139) with large variance. Similar problem applies to the Monte Carlo simulation that tilts the probability measure to 2 PA 2 ; this Monte Carlo simulation is inadequate to esti- mate . But tilting the probability measure to 1 PA 2 is better than tilting the probability to1 since the event A2 constitutes the bulk of the event that the portfolio loss exceeds . Note that both important sampling methods mentioned above are less efficient than the primitive Monte Carlo simulation (that samples the stock return form ). On the other hand, the hybrid importance sampling algorithm performs better than the primitive Monte Carlo simulation. It produces accurate probability estimation and reduces the variance at a ratio of 7 6 2.28 10 3.55 10 1/1 5 stock return to 1 P (or 2 P ) also performs poorly in this case. Note that the hybrid importance sampling algorithm still outperforms the primitive Monte Carlo simulation by reducing the variance at a ratio of 7 6 5.44 10 1/7.5 4.05 10 . 5 Conclusions The paper improves the performance for estimating VaR. We first extend Glasserman’s importance sampling method to Merton’s jump diffusion process. Then we suggest a novel Monte Carlo simulation, the hybrid im- portance sampling algorithm, which can efficiently esti- mate the VaR of complex financial portfolios. Numerical results given in this paper verify that our method greatly improve the performance. 6. Acknowledgement . In other words, the sample size of the primitive Monte Carlo simulation should be 15 times the sample size of the hybrid importance sampling algorithm to make the former method achieve the same accuracy level as the latter method. We thank Shi-Gra Lin, and Ren-Her Wang for useful suggestions. REFERENCES [1] S. K. Lin, C. D. Fuh, and T. J. Ko, “A bootstrap method with importance resampling to evaluate value-at-risk,” J. Financial Studies, Vol. 12, pp. 81–116, 2004. In Table 3, the probability that the portfolio loss ex- ceeds is larger (about 0.0403) since the jumps in stock price make the huge loss events A1 and A2 more likely to happen. Naively tilting the probability measure of the [2] H. G. Fong and K. C. Lin, “A new analytical approach to value at risk,” J. Portfolio Management, Vol. 25, pp. 88–97, 1999. Table 2. Compare monte carlo simulations under the log- normal stock price model [3] P. Glasserman, P. Heidelberger, and P. Shahabuddin, Vaniance Reduction Technique for Estimating Value-at- Risk, Management Sci., Vol. 46, pp. 1349–1364, 2000. Prob- ability Meas- ure 1 Hybrid 2 p [4] E. Eberlein, U. Keller, and K. Prause, “New insights into smile, mispricing, and value-at-risk: The hyperbolic model, J. Business, Vol. 71, pp. 371–406, 1998. 0.0349 0.0139 0.0395 0.0349 [5] J. R. M. Hosking, G. Bonti, and D. Siegel, “Beyond the Lognormal,” Risk, Vol. 13, pp. 59–62, 2000. p 36 55 10 . 3 4.14 10 3 2.5 7 2 10 2.28 10 Var( ) [6] K. Koedijk, R. Huisman, and R. Pownall, “VaR-x: Fat tails in financial risk management,” J. Risk 1, pp. 47–62, 1998. Consider a short straddle option that contains a short position in 1 unit call option and 1 unit put option . The probability for the portfolio to lose more than 5% of the stock price in 0.008 year is estimated in column 2 (i.e.,and ). The stock av- erage annual return μ is 0.05, the annual volatility of the stock price σ is 0.3, anddefined in Equation (9) is 0.01. Note that the jump fre- quency λ is 0 in this case. 11 21 0.05S t *0.05r [7] P. Glasserman, P. Heidelberger, and P. Shahabuddin, “Portfolio value-at-risk with heavy-tailed risk factors,” Math. Finance, Vol. 12, pp. 239–269, 2002. [8] R. C. Merton, “Option pricing when underlying stock returns are discontinuous,” J. Financial Econ., Vol. 3, pp. 125–144, 1976. * 0 r [9] J.-C. Duan, “The GARCH option pricing model,” Math. Finance, Vol. 5, pp. 13–32, 1995. Table 3. Compare monte carlo simulations under the mer- ton’s jump diffusion stock price model [10] S. Heston, “A closed-form folution for options with stochas- tic volatility with applications to bond and currency op- tions,” Rev. Financial Studies, Vol. 6, pp. 327–343, 1993. Prob- ability Meas- ure 1 2 Hybrid p 0.0405 0.0363 0.0426 0.0403 Var( [11] P. Jorion, Value at risk, McGraw-Hill, New York, 1997. [12] C. Rouvnez, Going Greek with VaR, Risk 10 (1997) 57–65. p ) 6 4.05 10 2 1.97 10 s 4 6.2 7 1 10 5.44 10 [13] F. Black and M. Scholes, “The pricing of options and corporate liabilities,” J. Political Econ., Vol. 81, pp. 637–659, 1973. The numerical settings follow the settings listed in Table 2 except that the jump frequency λ is 6, the mean of jump size η is 0, and the stan- dard derivation of jump size δ is 0.03. |

