Theoretical Economics Letters, 2011, 1, 57-62
doi:10.4236/tel.[phone] Published Online November 2011 (http://www.SciRP.org/journal/tel)
Licensing Contracts in Hotelling Structure
Tarun Kabiraj1, Ching Chyi Lee2
1Indian Statistical Institute, Kolkata, India
2The Chinese University of Hong Kong, Hong Kong, China
Received June 1, 2011; revised August 11, 2011; accepted August 22, 2011
Abstract
This paper discusses the question of optimal licensing contracts in Hotelling structure and focuses on the
unique features of this structure in this context. We show that a royalty equilibrium exists if and only if
transport cost lies in a specified interval, but the royalty rate can be higher than the amount of cost saving.
While fee licensing only is never profitable, the optimal licensing contract consists of both fee and royalty. In
equilibrium the market is fully covered with monopolistic goods.
Keywords: Technology Transfer, Royalty Licensing, Fee Licensing, Hotelling Structure
1. Introduction
Technology transfer from a low cost firm to a high cost
firm is a common phenomenon. By transferring its supe-
rior technology the patent holder can achieve a larger
profit. There is already a vast literature on technology
licensing. One aspect of this literature is to discuss the
question of optimal licensing contracts1. Generally tech-
nology transfer occurs under a fee contract or royalty
contract, and sometimes the contract takes a hybrid form
consisting of both fee and royalty2. However, which par-
ticular form of contract is optimal from the viewpoint of
the transferor depends on a number of factors such as:
the structure of the product market, the nature of market
competition, the degree of product differentiation, the
extent of cost saving, whether the patentee is an insider
or outsider, whether there is asymmetric information, etc.
Given the existing literature, it seems that the question
of technology licensing in the Hotelling [5] structure is
not yet fully explored. One motivation of the present
paper is to draw attention to the special features of the
Hotelling model in this context as distinct from the other
models of product differentiation. The important ques-
tions we like to discuss in this paper are the following.
Can there be a technology transfer under a fee contract?
Does a royalty contract always exist? Is the market fully
covered under the optimal licensing contract? Can the
optimal royalty rate exceed the extent of cost saving?
Can the transferor extract all surplus of the transferee by
means of a royalty alone? Is such transfer beneficial to
the consumers? We restrict our analysis to the scenario
where the patentee is an insider and firms’ locations are
exogenous. Initially the firms have asymmetric tech-
nologies. The low cost firm then designs a contract to
transfer its technology to the other firm.
To our knowledge, only two papers, Poddar and Sinha
[6] and Matsumura and Matsushima [7], have provided
some analysis on the issue of technology licensing in
Hotelling structure. While Poddar and Sinha discuss the
question of optimal licensing contracts between the two
firms, their solution for a royalty contract is incorrectly
formulated. And Matsumura and Matsushima examine
how licensing activities affect the location of the firms
and their incentives for R & D investment. Both the pa-
pers assume a priori that a royalty cannot exceed the
amount of cost saving, but neither explains why such an
assumption is needed. In our paper we investigate this
issue when the royalty rate is endogenously determined.
Further, in our analysis there is an outside good; hence
we examine whether in equilibrium the market is fully
covered with the monopolistic good. In all the models,
however, fee licensing is never profitable.
The main results derived in the paper are the following,
and it may be pointed out that some of these results are
driven by the unique qualities of the Hotelling model of
duopoly. For instance, we show that the optimal output
and profit levels are independent of the marginal cost of
production when the firms are equally efficient; so with
1See, for instance, Kabiraj [1], Sen and Tauman [2]), and Mukherjee
[3].
2In a survey of firms, Rostoker [4] finds that 39% of cases have royalty
alone, 13% have fee alone and the remaining cases have fee plus roy-
alty.

T. KABIRAJ ET AL.
58
technology transfer marginal cost has no effect on the
equilibrium levels of market share or firm profits. In ad-
dition, under transfer the transferee’s profit is unaffected
by the royalty rate and the transferor’s profit is linear in
royalty rate. In no other differentiated product models we
have these features. In our paper the transport cost plays
an important role in determining and characterizing the
licensing equilibrium. A royalty licensing equilibrium
exists if and only if the transport cost belongs to a speci-
fied interval. In equilibrium the market is fully covered;
thus segmented market equilibrium will never occur. The
optimal royalty rate when licensing equilibrium exists
can be higher than the amount of cost reduction. Since
the transferor cannot extract all surplus of the transferee
by means of a royalty only, a royalty-fee contract is op-
timal in the Hotelling structure.
To briefly outline the literature in his context, we note
that in a homogeneous good duopoly, with the patentee
being insider, in equilibrium royalty licensing dominates
fee licensing and the optimal royalty is equal to the
amount of cost saving (Wang [8]). Then if the model is
extended to the case of usual Dixit [9] type product dif-
ferentiation, qualitative results remain almost unchanged
(Wang [10]). One distinctive result, however, is that a
drastic innovation may be transferred when the goods are
imperfect substitute. Li and Song [11] have studied
technology licensing in a vertically differentiated du-
opoly. It is shown that the high-quality firm always
transfers its superior technology to the low-quality firm,
irrespective of the forms of the licensing contracts. Fi-
nally, Kabiraj and Lee [12] have shown that when the
products are both vertically and spatially differentiated a
fee licensing can be a profitable option.
The layout of the paper is the following. In section 2
we present the model and results. Finally, section 3 is a
conclusion.
2. Model and Results
Consider two firms producing homogeneous goods but
located at two end points of a Hotelling linear city of
length 1. Assume that firm 1 is located at 0 and firm 2 at
1. Consumers are uniformly distributed over the length
of the city; each consumer buys at most one unit of the
monopolistic good. We say that the market is fully cov-
ered if all consumers buy the good. Assume further that
there is an outside competitive good, and the consumer’s
net utility from it is normalized to zero. Therefore a
consumer will buy the monopolistic good if and only if
her net utility from it is non-negative.
The utility function of a consumer located at
is given by
[0,1]x
1
2
if tobuyfromfirm1
(1) iftobuyfromfirm2
vtxp
uvtx p




where denotes the basic utility, same for all con-
sumers; i is the unit price charged by firm , and
is the Hotelling transport cost of travel per unit
distance. We restrict to the scenario where each firm has
a positive market share; therefore,
0v
pi
0t
i; jj
ptpptij

 
.
Let
x
be the consumer indifferent between buying
from firm 1 and firm 2,

21
1
2
x
tp p
t

Then the market is fully covered if and only if
12. This gives demand for firm 1 and firm
2’s product as
2vp pt
11 2
(, )Dpp x and 212 (, )1Dpp x

,
respectively. On the other hand, the market is segmented
if 12 2vp pt

. This is the situation when some
consumers (in particular, the one located at
x
) fail to
buy the monopolistic product. In this case firm i
(i1, 2

) faces the demand, i
ii
() vp Dp t

.
Let i be the unit cost of production of firm . Fur-
ther assume that firm 2 possesses the superior technology;
therefore, 21
ci
cc

. We consider the possibility of tech-
nology transfer from firm 2 to firm 1. First we consider
the benchmark case of no technology transfer. Then we
examine fee licensing and royalty licensing separately.
Finally we discuss the optimal licensing contract.
2.1. Benchmark Case: No-Transfer of
Technology
Given the demand and cost functions, firm i’s profit
function is:
i12i i i12
(, )()(, )ppp cDpp

 i1,2

We assume that both the firms have positive market
shares. The firms simultaneously choose their prices,
hence they play a Bertrand-Nash game. The equilibrium
prices, market shares and profits of the firms are

112
132
3
N
ptcc,

21
132
3
N
ptc
2
c

12
13
6
NN
Dx tcc
t1

,

21
1
13
6
NN
Dx tc
t
 2 c

2
121
1
π3
18
Ntc c
t
,

2
21
1
π3
18
Ntc c
t

2

59 T. KABIRAJ ET AL.
Then, the assumption that each firm has a positive mar-
ket share means that
12
3
cc
t

t
(1)
2.2. Technology Transfer under a Fee Contract
Here the game is the following. Firm 2 offers a fee con-
tract to firm 1. If it is accepted, the superior technology is
transferred and the market structure becomes symmetric
duopoly, with each firm having low unit cost of produc-
tion. And if the contract is rejected (this is equivalent to
giving a no-technology transfer offer), the market struc-
ture becomes asymmetric duopoly as given in the ben-
chmark model.
Now the market-operated profits of the firms under the
fee licensing contract are:
12
ππ
2
F
F
t

Then technology transfer under the fixed fee contract
F
will be mutually profitable if and only if
22
ππ
F
N
F and 1 π1 π
F
N
F . Then if and
only if
0F
121
ππ ππ
2
F
FN

N

But this condition is never satisfied. Hence in the Ho-
telling structure fee licensing will never occur in equilib-
rium3.
2.3. Technology Transfer under a Royalty
Contract
Now consider the possibility of technology transfer from
firm 2 to firm 1 under a royalty contract. The game is the
following. First, firm 2 proposes a royalty, , per unit of
firm 1’s output. In the second stage firm 1 either accepts
or rejects the contract; it accepts if it is not worse off in
the post-transfer situation. Then in the third stage they
choose prices simultaneously. Therefore, rejecting the
contract means it is no-transfer equilibrium outcome.
r
First consider royalty equilibrium with full market
coverage. Given any , the third stage problems of firm
1 and firm 2 are respectively,
r
1
12 112
max ()(,)
ppcrDpp
and
2
22 212112
max ()(,)(,)
ppcDpp rDpp
The third stage outcomes are:
12 2
() ()
RR
prprtc r
12
1
()() 2
RR
Dr Dr


1
π() 2
Rt
r

and 2 π() 2
Rt
rr
Recall that the assumption of full market coverage re-
quires that , i.e.,
12
2()()
RR
vpr prt
2
3
R
2
rvc tr (2)

 
We further need to restrict that , i.e., 0
R
r
2
2()
3
tvct

 (3)
Note the unique features of the Hotelling structure in
licensing equilibrium. Here 1
R
D, 2
R
D and 1 π
R
are in-
dependent of , but 1
r
R
p, 2
R
p and 2 π
R
are linear and
increasing in . Hence firm 2 has an incentive to in-
crease as much as possible; in response firm 1 will
just raise its price linearly without losing its market share
and profits as long as the indifferent consumer
r
r
x
con-
tinues to buy. Therefore, the optimal royalty
R
r is de-
termined corresponding to () 0ux. This gives
2
3
2
R
rvc t (4)
Given that tt (which ensures that both the firms’
market shares are positive and profits are strictly posi-
tive), we have 11 π() π
R
N
r. Therefore, in the second stage
any royalty
R
rr

is acceptable to firm 1. Given (4), there
are parameter values under which 12 is
possible; therefore the royalty rate can exceed the
amount of cost saving.
()
R
rcc 0
Now firm 2 will offer the royalty
R
r iff 22
ˆ
π() π
R
N
r,
that is
2
12
1(3 )
218
Rt
rtc
t
 c

2
12 12
2
()( 3
() 23 18
()
cc cc
LHS tvctt
RHS t

 

)
(5)
Check that is linear anddecreasing in , and
is convex and decreasing, with
()LHS tt
()RHS t
12
()cc
() 3 RHS t as , and t () ()LHS tRHS t.
Therefore,
ˆˆ
, , |LHS()RHS() (,)tt ttttttt ˆ (6)
This is shown in Figure 1. Thus royalty equilibrium is
the subgame perfect Nash equilibrium outcome of this
game if the transport cost lies in the specified interval.
This gives the first result of our paper.
3This result is already derived in Poddar and Sinha [6]. However, fee
licensing can be profitable if the products are both vertically and hori-
zontally differentiated (Kabiraj and Lee [12]).
Proposition 1: Technology transfer under the royalty
contract with full market coverage is mutually profitab le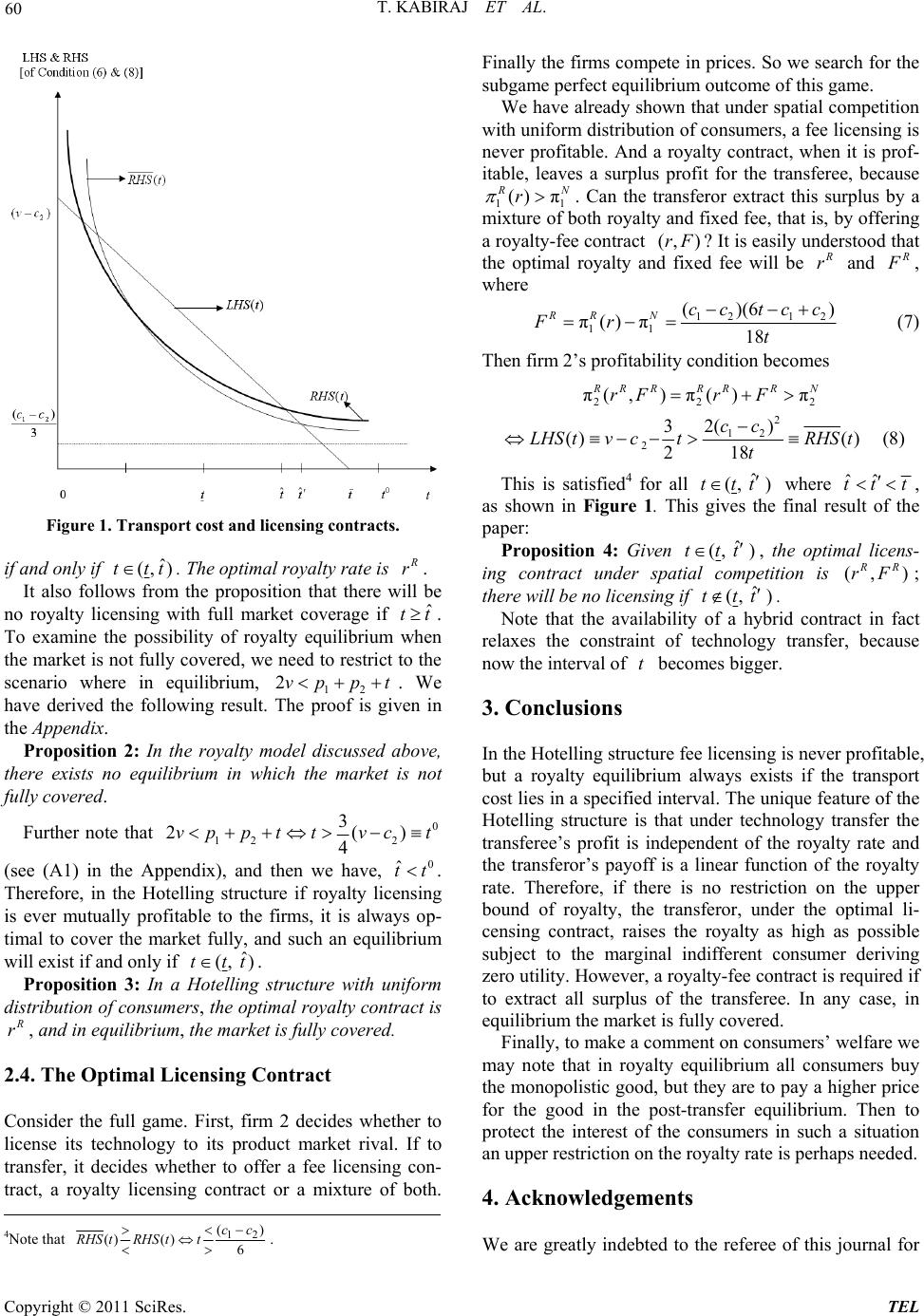

T. KABIRAJ ET AL.
60
Figure 1. Transport cost and licensing contracts.
if and only if ˆ (, )ttt. The optimal royalty rate is
R
r.
It also follows from the proposition that there will be
no royalty licensing with full market coverage if .
To examine the possibility of royalty equilibrium when
the market is not fully covered, we need to restrict to the
scenario where in equilibrium, 12 . We
have derived the following result. The proof is given in
the Appendix.
ˆ
tt
t2vpp
Proposition 2: In the royalty model discussed above,
there exists no equilibrium in which the market is not
fully covered.
Further note that 0
12 2
3
2(
4
vp pttvct)
(see (A1) in the Appendix), and then we have, 0
ˆ
tt

.
Therefore, in the Hotelling structure if royalty licensing
is ever mutually profitable to the firms, it is always op-
timal to cover the market fully, and such an equilibrium
will exist if and only if ˆ
(, )ttt.
Proposition 3: In a Hotelling structure with uniform
distribution of consumers, the op timal royalty contract is
R
r, and in equilibrium, the market is fully covered.
2.4. The Optimal Licensing Contract
Consider the full game. First, firm 2 decides whether to
license its technology to its product market rival. If to
transfer, it decides whether to offer a fee licensing con-
tract, a royalty licensing contract or a mixture of both.
Finally the firms compete in prices. So we search for the
subgame perfect equilibrium outcome of this game.
We have already shown that under spatial competition
with uniform distribution of consumers, a fee licensing is
never profitable. And a royalty contract, when it is prof-
itable, leaves a surplus profit for the transferee, because
11
() π
R
N
r  . Can the transferor extract this surplus by a
mixture of both royalty and fixed fee, that is, by offering
a royalty-fee contract ? It is easily understood that
the optimal royalty and fixed fee will be
(, )rF
R
r and
R
F
,
where
12 12
11
()(6
π() π
18
RR N
cc tcc
Fr t

 )
2
(7)
Then firm 2’s profitability condition becomes
22
π(, )π() π
R
RRRRRN
rFr F
2
12
2
2( ) 3
() ()
218
cc
LHStvctRHSt
t

  (8)
This is satisfied4 for all ˆ
(, )ttt

 where ˆˆ
tt t


,
as shown in Figure 1. This gives the final result of the
paper:
Proposition 4: Given ˆ (, )ttt

, the optimal licens-
ing contract under spatial competition is (, )
R
R
rF ;
there will be no licensing if ˆ
(, )ttt

.
Note that the availability of a hybrid contract in fact
relaxes the constraint of technology transfer, because
now the interval of becomes bigger.
t
3. Conclusions
In the Hotelling structure fee licensing is never profitable,
but a royalty equilibrium always exists if the transport
cost lies in a specified interval. The unique feature of the
Hotelling structure is that under technology transfer the
transferee’s profit is independent of the royalty rate and
the transferor’s payoff is a linear function of the royalty
rate. Therefore, if there is no restriction on the upper
bound of royalty, the transferor, under the optimal li-
censing contract, raises the royalty as high as possible
subject to the marginal indifferent consumer deriving
zero utility. However, a royalty-fee contract is required if
to extract all surplus of the transferee. In any case, in
equilibrium the market is fully covered.
Finally, to make a comment on consumers’ welfare we
may note that in royalty equilibrium all consumers buy
the monopolistic good, but they are to pay a higher price
for the good in the post-transfer equilibrium. Then to
protect the interest of the consumers in such a situation
an upper restriction on the royalty rate is perhaps needed.
4. Acknowledgements
4Note that 12
()
() ()6
cc
RHS tRHS tt



. We are greatly indebted to the referee of this journal for

T. KABIRAJ ET AL.
61
his valuable suggestions and comments on the earlier
draft. We shall, however, be held responsible for any re-
maining errors.
5. References
[1] T. Kabiraj, “Technology Transfer in a Stackelberg Struc-
ture: Licensing Contracts and Welfare,” The Manchester
School, Vol. 73, No. 1, 2005, pp. 1-28.
doi:10.1111/j.1467-9957.2005.00421.x
[2] D. Sen and Y. Tauman, “General Licensing Schemes for
a Cost-Reducing Innovation,” Games and Economic Be-
havior, Vol. 59, No. 1, 2007, pp. 163-186.
doi:10.1016/j.geb.2006.07.005
[3] A. Mukherjee, “Competition and Welfare: The Implica-
tions of Licensing,” The Manchester School, Vol. 78, No.
1, 2010, pp. 20-40.
doi:10.1111/j.1467-9957.2009.02126.x
[4] M. Rostoker, “A Survey of Corporate Licensing”, IDEA:
The Journal of Law and Technology, Vol. 24, No. 2, 1984,
pp. 59-92.
[5] H. Hotelling, “Stability in Competition,” Economic Jour-
nal, Vol. 39, No. 153, 1929, pp. 41-57.
doi:10.2307/2224214
[6] S. Poddar and U. Sinha, “On Patent Licensing in Spatial
Competition,” The Economic Record, Vol. 80, No. 249,
2004, pp. 208-218.
doi:10.1111/j.1475-4932.2004.00173.x
[7] T. Matsumura and N. Matsushima, “On Patent Licensing in
Spatial Competition with Endogenous Location Choice,”
2008. http://www.iss.u-tokyo.ac.jp/~matsumur/LI.pdf
[8] X. H. Wang, “Fee versus Royalty Licensing in a Cournot
Duopoly Model,” Economics Letters, Vol. 60, No. 1, 1998,
pp. 55-62. doi:10.1016/S0165-1765(98)00092-5
[9] A. Dixit, “A Model of Duopoly Suggesting a Theory of
Entry Barriers,” Bell Journal of Economics, Vol. 10, No.
1, 1979, pp. 20-32. doi:10.2307/3003317
[10] X. H. Wang, “Fee versus Royalty Licensing in a Differ-
entiated Cournot Duopoly,” Journal of Economics and
Business, Vol. 54, No. 2, 2002, pp. 253-266.
doi:10.1016/S0148-6195(01)00065-0
[11] C. Li and J. Song, “Technology Licensing in a Vertically
Differentiated Duopoly,” Japan and the World Economy,
Vol. 21, No. 2, 2010, pp. 183-190.
doi:10.1016/j.japwor.2008.04.002
[12] T. Kabiraj and C. C. Lee, “Technology Transfer in a Du-
opoly with Horizontal and Vertical Product Differentia-
tion,” Trade and Development Review, Vol. 4, No. 1, 2011,
pp. 19-40.

T. KABIRAJ ET AL.
62
Appendix
To examine the possibility of royalty equilibrium
when the market is not fully covered let us restrict to the
scenario where in equilibrium, .
12
Consider local monopoly of firm 1 under technology
transfer. For any acceptable , firm 1’s problem is:
2vp pt
r
1
1
12
max ()
p
vp
pcrt


The corresponding product price and market share of
firm 1 are, respectively,
12
1
() ()
2
prvcr
 and 1
1
() ()
2
Drv cr
t


2
r
Since now two markets are segmented, the licensing revenue
maximizing royalty rate will be , where
1
r
argmax( )rrD 
2
vc
2
r



The corresponding equilibrium price, market share and
profit of firm 1 are:
12
1
() (3)
4
prvc
 , 12
1
() ()
4
Drv c
t


and 2
12
1
π()( )
16
rvc
t


and the royalty income of firm 2 is,
2
12
1
() ()
8
rD rvc
t



Firm 2’s profit from its segmented market is solved
from:
2
2
22
max ()
p
vp
pc t


This gives:
22
1()
2
pvc
, 12
1()
2
Dvc
t


and 2
22
1
π()
4vc t


Hence, firm 2’s total payoff under royalty licensing is:
2
22 12
3
π() ()
8
rD rvc
t
 
 
Finally, the licensing contract with local monop-
oly will be an equilibrium contract iff the following three
conditions hold simultaneously. First, the assumption that
each firm has local monopoly requires ,
i.e.,
r

12
2vp pt

0
2
3()
4
tvct
1
(A1)
Second, the contract on is acceptable to firm 1 iff
, i.e.,
r

0
1
π() πr

212
1
3
22
vcc c
tt



2
(A2)
Third, offering the licensing contract is profitable to
firm 2 iff
r

0
2
π


, i.e.,

12
2
3
23
cc
tvc

2
t

  (A3)
These three conditions (A1) through (A3) will be satis-
fied simultaneously iff
0
12
min{ ,}tt t (A4)
Therefore,
2
tt

1


12
2
3(232)
()
42
cc
vc 3



Finally, we can check that ; therefore con-
dition (A4) is never satisfied. This proves Proposition 2.
0
12
min{ ,}ttt