Applied Mathematics
Vol. 3 No. 11A (2012) , Article ID: 24759 , 8 pages DOI:10.4236/am.2012.331247
Upwind Finite-Volume Solution of Stochastic Burgers’ Equation
1Department of Engineering Mathematics & Physics, Engineering Faculty, Cairo University, Giza, Egypt
2Department of Engineering Mathematics & Physics, Faculty of Engineering, Fayoum University, Fayoum, Egypt
Email: zbeltagy@hotmail.com, mibrwafa@yahoo.com, ohgalal2010@yahoo.com
Received August 9, 2012; revised September 9, 2012; accepted September 16, 2012
Keywords: Polynomial Chaos Expansion; Stochastic Burgers’ Equation; Upwind Finite-Volume Technique
ABSTRACT
In this paper, a stochastic finite-volume solver based on polynomial chaos expansion is developed. The upwind scheme is used to avoid the numerical instabilities. The Burgers’ equation subjected to deterministic boundary conditions and random viscosity is solved. The solution uncertainty is quantified for different values of viscosity. Monte-Carlo simulations are used to validate and compare the developed solver. The mean, standard deviation and the probability distribution function (p.d.f) of the stochastic Burgers’ solution is quantified and the effect of some parameters is investigated. The large sparse linear system resulting from the stochastic solver is solved in parallel to enhance the performance. Also, Monte-Carlo simulations are done in parallel and the execution times are compared in both cases.
1. Introduction
In engineering fields, most models are represented as partial differential equations (PDEs), assuming all input data are perfectly known. Unfortunately, geometry and material characteristics for instance would rather present uncertainties. Under those conditions, the output data become also uncertain. To deal with propagation of the input data uncertainties to the output data, probabilistic models are more appropriate than deterministic ones. Several methods of solution are developed to assess the response due to the uncertainties. This response depends on two main factors: the first factor is the geometric domain discretization; the second is the discretization involved random process [1,2]. The methods of solution may be classified according to the first factor to meshless methods [3], stochastic finite difference methods [4], and stochastic finite element methods [5]. On the other hand, according to the second factor the methods of solution may be classified to Monte-Carlo simulations (MCS) [6], perturbations [7], and spectral stochastic finite element methods (SSFEM) [8,9]. Recently, the SSFEM is one of the most widely used methods [7].
On the other hand, the capability of neural network to analyze stochastic finite element is discussed by Hurtado [10]. He discussed simple beam with stochastic modulus of elasticity and deterministic load. Homogenous chaos expansion Radial basis (RBF) neural network was trained with some pairs of input and output by MCS simulations. Later, El-Beltagy et al. [11] developed this method to include the effect of random load and random modulus of elasticity using both of RBF neural network and polynomial chaos expansion (PCE).
Burgers’ equation is an important partial differential equation from fluid dynamics, and is widely used for various physical applications, such as modeling of gas dynamics and traffic flow, shock waves [12], investigating the shallow water waves [13,14], in examining the chemical reaction diffusion model of Brusselator etc. [15]. In fact, it can be used as a model for any nonlinear wave propagation problem subject to dissipation [16]. Depending on the problem being modeled, this dissipation may result from viscosity, heat conduction, mass diffusion, thermal radiation, chemical reaction, or other source. Burgers’ equation may be analyzed by using the exact shock-wave solution. In the current paper, finite-volume upwind technique is used to avoid the numerical instabilities and compute solution for small viscosity as discussed by Stephens et al. [17].
The SSFEM, and also the stochastic finite-volume, produces large sparse linear systems. Also, Burgers’ equation with zero or small viscosity will be hyperbolic PDE which produces stiff linear system and requires very small time steps to be solved adequately. To enhance the performance of the developed solver, parallelization should be considered. Additionally, MCS should be of order 104 or more for reliable comparisons. These simulations should be done in parallel as well. In the current paper, parallelization of both techniques is considered.
2. Polynomial Chaos Expansion
Polynomial chaos expansion has many advantages in evaluating both statistical moments of any order and the p.d.f of system response which represents a complete solution of the random systems. Ghanem and Spanos [8], evaluated the system response as a summation of nonlinear functional of a set of  multiplied by deterministic constants. The system response in terms of polynomial chaos is written in the form:
multiplied by deterministic constants. The system response in terms of polynomial chaos is written in the form:
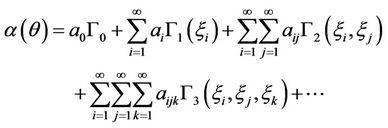 (1)
(1)
where  is the polynomial chaos of order
is the polynomial chaos of order  in a set of
in a set of  random variables
random variables 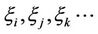 If the polynomial chaos are truncated at order
If the polynomial chaos are truncated at order  , the response of the system will be reduced to :
, the response of the system will be reduced to :
 (2)
(2)
where ci is a set of deterministic coefficients, and  is a set of polynomials of random variables, these polynomials are orthogonal.
is a set of polynomials of random variables, these polynomials are orthogonal.
3. Stochastic Finite-Volume Formulation for Burgers’ Equation
Consider the one dimensional Burgers’ equation [13,14]
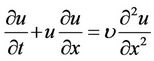 (3)
(3)
Subject to the following deterministic initial and boundary conditions:
 (4)
(4)
When the time derivative term is dropped from equation, and for large viscosity, we are left with an elliptic partial differential equation representing the steady-state balance between the convective and diffusive terms. The difficulty in computing solutions to the Burgers’ equation lies in the inability to effectively balance the nonlinear convective term, and the diffusive term. For zero (or small) viscosity, the equation tends to be hyperbolic and the solution technique should be adapted to account for the characteristics of the equation.
Considering  is a stochastic viscosity, the response will be also stochastic and they can both expanded using polynomial chaos expansion as:
is a stochastic viscosity, the response will be also stochastic and they can both expanded using polynomial chaos expansion as:
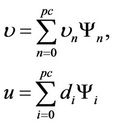 (5)
(5)
The number of polynomials ( ) is a function of the required order (p) and dimension (M). Then, the differential equation can be written as:
) is a function of the required order (p) and dimension (M). Then, the differential equation can be written as:
 (6)
(6)
Galerkin projection scheme can be applied to Equation (6) through multiplying both sides by Ψi and applying the expectation operator, yields:
 (7)
(7)
where,  ,
,  , then
, then
 (8)
(8)
Using the finite-volume node-centered approach by integrating over the control volume, yields:
 (9)
(9)
By using the upwind scheme for the face-centered values, then the differential equation is reduced to:
 (10a)
(10a)
or
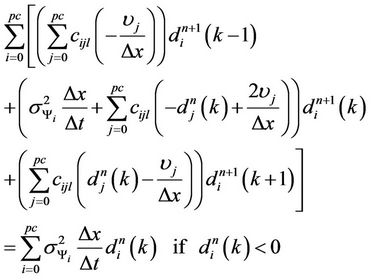 (10b)
(10b)
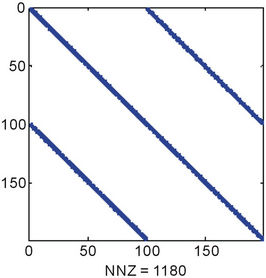
Equations (10a) and (10b) result in sparse linear system. The linear system becomes larger as the order and/or the dimension of the polynomial chaos are increased. Figure 1 shows the sparsity pattern when discretizing the domain into 100 divisions and for different values of the order and dimension. The number of nonzeros (NNZ) is shown below the figure of each case. Sparse storage should be considered to save the memory and to enhance the performance by using a suitable sparse linear solver.
4. Solution Techniques and Discussion
Consider the one dimensional viscous Burgers’ equation on the interval [0, 1] with Dirichlet boundary conditions; u = 1 at x = 0 and u = −1 at x = 1 respectively. The interval is discretized into N = 128 finite elements. Different values of order p and dimension M are used with different values of the mean viscosity 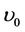 . In the current work, the stochastic variation of the viscosity is taken as:
. In the current work, the stochastic variation of the viscosity is taken as:

This means that the first stochastic component of the viscosity is only 20% of the mean value to avoid negative values of viscosity. Using the above proposed solver, we can notice that the effect of the mean viscosity on the solution. The larger the viscosity is, the smoother the solution is (parabolic behavior of Burgers’ equation). On the other hand, as the mean viscosity decreases (and may reach zero) the response will be similar to the hyperbolic wave equation and a shock wave (with zero velocity) will be constructed. Figure 2 shows the mean solution using both the stochastic solver and the MCS simulations. The mean solutions are in a good agreement for different values of the mean viscosity.
Figure 3 shows the convergence history of the stochastic finite volume solver for different mean values of viscosity. The residual logarithm is reduced up to −10. The figure shows that the number of iterations required for convergence increases as the mean value of the viscosity is decreased. Consequently the CPU time increases for small values of viscosity due to the slow rate
 (a)
(a)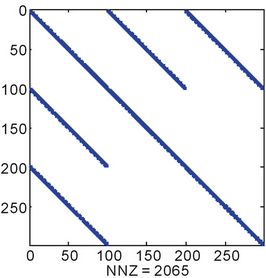 (b)
(b)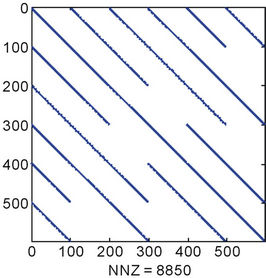 (c)
(c) (d)
(d)
Figure 1. Sparsity pattern for for different order (p) and different dimension (M). The number of nonzeros (NNZ) is shown. (a) p = 1, M = 1; (b) p = 1, M = 2; (c) p = 2, M = 2; (d) p = 2, M = 4.
 (a)
(a) (b)
(b)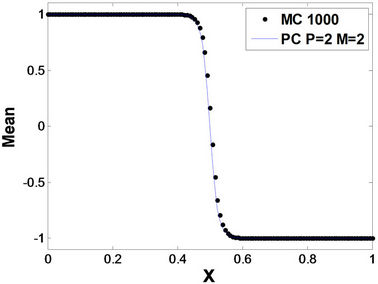 (c)
(c) (d)
(d)
Figure 2. Mean value of the stochastic solver and MCS for different values of mean viscosity. (a) Viscosity = 1.0; (b) Viscosity = 0.1; (c) Viscosity = 0.01; (d) Viscosity = 0.001.

Figure 3. Solver convergence (Log-Log scale) for different values of mean viscosity with p = 2 and M = 2.
of convergence and smaller time steps. The CPU time needed to solve the stochastic system is listed in Table (1). The used workstation was intel® xean® CPU X5690 3.47 GHz (6 cores), 8 GB RAM, 64-bit O.S. The PARDISO (Parallel Direct Solver) [18,19] is used in solving the stochastic linear system. The parameters of the PARDISO solver are set to utilize the 6 cores available on the workstation. More than 50% performance increase is obtained in solving the linear system when using PARDISO.
Additionally, the stochastic linear system can be constructed in parallel, but this was not done in the current work as it will consume more memory storage. The MCS simulations can be done by generating random normal distribution for a certain mean viscosity and use these values to run the deterministic finite-volume solver. The deterministic solver can be developed in a similar way as the above described stochastic solver. In the current work, the stochastic solver with zero order and zero dimension is used instead. This will assure that all parameters are the same when comparing the two solution techniques (Stochastic and MCS). The MCS simulations are done also in parallel. The MCS simulations are independent runs and hence the parallelization is straight forward using Open-MP support available with the current C++ compilers. Histograms of the stochastic values of viscosity with mean value of 0.1 is shown in Figure 4.
Table 1 shows the CPU time comparisons between the stochastic solver and the MCS simulations. It can be notice that using of stochastic solver decrease CPU time dramatically with acceptable accuracy.
The standard deviation of stochastic response of Burgers’ equation for different values of viscosity compared with MCS is shown in Figures 5 and 6. It can be noticed that the standard deviation shrinks vanishes around the midpoint for all values of the mean viscosity. The MCS simulations are in a good agreement with the stochastic solver for larger mean values of the viscosity. As the

Figure 4. Histogram of the random values of viscosity used in MCS with mean value = 0.1.

Table 1. Time comparison (seconds) between MCS and the stochastic solver for different mean viscosity, different order (p) and dimension (M).
mean viscosity decreases, the deviations with the MCS are increased. Figure 5(d) is the same as Figure 5(c) but with different domain to show the deviations when using both solution techniques. Similarly, Figures 6(a) and (b) are the same but with different domains.
Figure 7 shows the relative error in the mean and the standard deviation when using the two techniques. As it is shown in the figure, the relative error in the mean increases as the mean viscosity decreases. On the other hand, the relative error in the standard deviation decreases as the mean viscosity decreases.
Figure 8 shows the first stochastic solution component of the polynomial chaos expansion  for different values of the mean viscosity. As the viscosity decreases, the first stochastic component becomes localized around the midpoint and its magnitude increases. The other (higher) stochastic components are small compared to the first component. So, the first component is approximately equals to the standard deviation.
for different values of the mean viscosity. As the viscosity decreases, the first stochastic component becomes localized around the midpoint and its magnitude increases. The other (higher) stochastic components are small compared to the first component. So, the first component is approximately equals to the standard deviation.
Figure 9 shows the stochastic solution (mean plus first stochastic component) for different values of the mean viscosity. The first component is scaled up by a factor of 10 to clarify the effect on the stochastic response. There are irregularities in the solution due to the random variation of the viscosity. These irregularities may become very sharp even around the shock wave.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 5. Standard deviation of the stochastic solver and MCS for different values of mean viscosity. (a) viscosity = 1.0; (b) viscosity = 0.1; (c) viscosity = 0.01; (d) viscosity = 0.01.
 (a)
(a) (b)
(b)
Figure 6. Standard deviation of the stochastic solver and MCS for mean viscosity = 0.001. (a) and (b) are the same but different domain.
 (a)
(a) (b)
(b)
Figure 7. Relative error for the mean (a) and the standard deviation (b) using the stochastic solver and MCS for different values of viscosity.
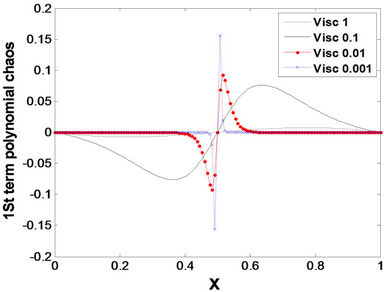
Figure 8. The first term polynomial chaos d1 of the stochastic response for different values of the mean viscosity with p = 2 and M = 2.

Figure 9. Mean solution plus the first stochastic component of the response obtained for different values of viscosity (the 1st stochastic component is scaled by a factor of 10).
Figure 10 illustrates the p.d.f of the solution at selected nodes for different values of the mean viscosity. The p.d.f is in a good agreement for larger values of the mean viscosity. As the mean viscosity decreases, the p.d.fs from both techniques deviate. The minimum and the maximum values of the response can be obtained easily, this issue is very important in the design stage and for reliability and safely analysis.
5. Conclusion
The stochastic finite-volume solution has advantages in evaluating the p.d.f of the system response with minimum cost. The developed solver based on the polynomial chaos expansion succeeds in analyzing stochastic nonlinear systems with high performance. Using the upwind scheme was proven as an appropriate choice to handle the system in the parabolic regime and also in the hyperbolic regime. The MCS simulations deviate from the stochastic solution when the system tends to be hyperbolic (mean viscosity decreases). Parallelization of the stochastic solver is important to increase the performance especially when solving the resulting linear sparse sys-
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 10. The p.d.f of stochastic solver and MCS for different values of mean viscosity: (a) at x = 0.5078, viscosity = 1.0; (b) at x = 0.3047, viscosity = 0.1; (c) at x = 0.4531, viscosity = 0.01; (d) at x = 0.4844, viscosity = 0.001.
tem. The stochastic solver developed in this work can be extended to higher dimensions in a straight forward way.
6. Acknowledgements
We should thank Prof. Magdy El-Tawil for his supervision and guidance to this work.
REFERENCES
- O. H. Galal, W. El-Tahan, M. A. El-Tawil and A. A. Mahmoud, “Spectral SFEM Analysis of Structures with Stochastic Parameters under Stochastic Excitation,” Structural Engineering and Mechanics, Vol. 28 No. 3, 2008, pp. 281-294.
- O. H. Galal, “The Solution of Stochastic Linear Partial Differential Equation Using SFEM through Neumann and Homogeneous Chaos Expansions,” Ph.D. Thesis, Cairo University, Cairo, 2005.
- S. Rahman and H. Xu, “A Meshless Method for Computational Structure Mechanics,” International Journal for Computational Methods in Engineering Science and Mechanics, Vol. 6, No. 1, 2005, pp. 41-58. doi:10.1080/15502280590888649
- M. Kaminski, “Stochastic Perturbation Approach to Engineering Structure Variability by the Finite Difference Method,” Journal of Sound and Vibration, Vol. 251 No. 4, 2002, pp. 651-670. doi:10.1006/jsvi.2001.3850
- G. Stefanou, “The Stochastic Finite Element Methods: Past, Present and Future,” Computer Methods in Applied Mechanics and Engineering, Vol. 198, No. 9-12, 2009, pp. 1031-1051. doi:10.1016/j.cma.2008.11.007
- M. Shinozuka and T. Nomoto, “Response Variability Due to Spatial Randomness of Material Properties,” Technical Report, Columbia University, New York, 1980.
- A. Henriques, J. Veiga, J. Matos and J. Delgado, “Uncertainty Analysis of Structural Systems by Perturbation Techniques,” Journal of Structural and Multidisciplinary Optimization, Vol. 35 No. 3, 2008, pp. 201-212. doi:10.1007/s00158-007-0218-z
- R. Ghanem and P. D. Spanos, “Stochastic Finite Elements: A Spectral Approach,” 2nd Edition, Dover, New-York, 2002.
- H. Panayirci, “Computational Strategies for Efficient Stochastic Finite Element Analysis of Engineering Structures,” Ph.D. Thesis, University of Innsbruck, Innsbruck, 2010.
- J. Hurtado, “Analysis of One Dimensional Stochastic Finite Element Using Neural Network,” Probabilistic Engineering Mechanics, Vol.17, No. 1, 2001, pp. 35-44.
- M. A. El-Beltagy, O. H. Galal and M. I. Wafa, “Uncertainty Quantification of a 1-D Beam Deflection Due to Stochastic Parameters,” International Conference on Numerical Analysis and Applied Mathematics, Halkidiki, 19-25 September 2011, pp. 2000-2003. doi:10.1063/1.3637007.
- J. D. Cole, “On a Quasilinear Parabolic Equations Occurring in Aerodynamics,” Quarterly of Applied Mathematics, Vol. 9, 1951, pp. 225-236.
- J. D. Logan, “An Introduction to Nonlinear Partial Differential Equations,” Wily-Interscience, New York, 1994.
- L. Debtnath, “Nonlinear Partial Differential Equations for Scientist and Engineers,” Birkhauser, Boston, 1997.
- G. Adomian, “The Diffusion-Brusselator Equation,” Computers & Mathematics with Applications, Vol. 29, No. 5, 1995, pp. 1-3. doi:10.1016/0898-1221(94)00244-F
- C. Fletcher, “Burgers’ Equation: A Model for All Reasons,” Numerical Solutions of Partial Differential Equations, North-Holland Pub. Co., Holland, 1982.
- A. B. Stephens, R. B. Kellogg and G. R. Shubin, “Uniqueness and the Cell Reynolds Number,” SIAM Journal on Numerical Analysis, Vol. 17, No. 6, 1980.
- O. Schenk and K. Gärtner, “Solving Unsymmetric Sparse Systems of Linear Equations with PARDISO,” Journal of Future Generation Computer Systems, Vol. 20, No. 3, 2004, pp. 475-487. doi:10.1016/j.future.2003.07.011
- O. Schenk and K. Gärtner, “On Fast Factorization Pivoting Methods for Symmetric Indefinite Systems,” Electronic Transactions on Numerical Analysis, Vol. 23, 2006, pp. 158-179.

