Open Journal of Applied Sciences
Vol.05 No.06(2015), Article ID:57450,8 pages
10.4236/ojapps.2015.56031
Evaluation of Thixotropic Models for Waxy Crudes
<img src=http://html.scirp.org/file/8-2310429x1.png width=426.25 height=10.1250004768372 />
*Corresponding author.
Liping Guo*, Xu Chen, Shuang Shi, Yu Wang, Xiaoyang Yu
College of Petroleum Engineering, Northeast Petroleum University, Daqing, China
Email: *glp_dqsy@sina.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 9 June 2015; accepted 23 June 2015; published 26 June 2015

ABSTRACT
Thixotropy is a great rheological behavior of waxy crudes oils and is of great importance for hydraulic characteristics and security of oil pipeline restart. In this paper, through the experiment of four waxy crudes, three kinds of thixotropic rheology characteristics in the conditions that shear stress decays under a constant shear rate, shear stress decays after shear rate steps up and hysteresis loop of shear rate cycle changes are studied . For eight thixotropic models, experimental data are fitted in the method of least-squares and average deviation is taken as a statistical indicator to evaluate the thixotropic models. It shows that the model with the idea of Cheng that completely reversible and totally irreversible structures both exist in waxy oil products and based on Houska model can describe thixotropic behaviors of waxy crudes most well.
Keywords:
Waxy Crude Oils, Thixotropy, Thixotropic Model

1. Introduction
Thixotropy is a great rheological behavior of many materials including waxy crude oils and is of great importance for hydraulic characteristics and security of oil pipeline restart. It can be described that due to the difference between failure rate and recovery rate of internal structure of the fluid system, under the effect of shear stress, the apparent viscosity continuously decreases with time and recovers gradually over time after stress relieving [1] . Thixotropic is the basic information for calculation of waxy crude oil pipeline restarting and pumpability evaluation of crude. And accurate quantitative description of the thixotropic behavior of waxy crude oil is necessary for the safety analysis of pipeline operation.
Domestic and foreign scholars had a wide range of studies for thixotropic fluid including crude and made a number of mathematical models used to describe the characteristics of thixotropic fluid [2] . Cheng put forward the properties of thixotropic fluid under the condition of constant shear rate, shear rate loaded that steps up and shear rate that changes continuously for shearing repeatedly [3] , but the existing mathematical models are mainly based on attenuation characteristic of the shear stress during the thixotropic process under the condition of constant shear rate loaded [4] -[7] . For the thixotropy of blood, the mathematical model of hysteresis thixotropic loop is proposed under the condition of shear rate that changes continuously by Huang [8] . For the thixotropy of waxy crude oils, though there are many researches, people rarely study the hysteresis thixotropic loop under the condition of shear rate that changes continuously and the attenuation characteristic of shear stress under the condition of shear rate loaded that steps up. However in the actual process of crude oil pipeline, shear rate is not constant but continually changing. For the rheology, the study of thixotropy should include the study of all rheological characteristics.
Through experiments in the paper, three thixotropic rheological characteristics above of waxy crude are studied and eight thixotropic models in the literature are evaluated.
2. Experiment
A stress-controlled rheometer (HAAKE RS150H) was used as an experimental apparatus. Table 1 shows an overview of basic properties of four waxy crudes used in this work.
The pretreated oil sample was heated to a heat-treating temperature as shown in Table 1 and taken into the measuring cylinder of rheometer. After holding for 5 min at the heat-treating temperature, the oil sample was statically cooled to a certain test temperature (near the freezing point) at a rate of 0.5˚C/min. The sample was held at the test temperature for another 40 min to ensure that the wax crystal structure could be fully developed. Then three kinds of thixotropy rheology characteristics measurement are made under the three loading condition of the constant shear rate, the shear rate that increases linearly and then reduces linearly and the shear rate that step up. The experimental data is recorded every second for model evaluation.
In this paper, experiment of four crude oils is done for each measurement temperature under the constant shear rate loaded including 1 s−1, 2 s−1, 4 s−1, 8 s−1, 16 s−1, 32 s−1 and the shear rate loaded that steps up. Each shear rate experiment adopts new sample and shear time is 10 min. Record data points per second.
During the hysteresis loop measurement, shear rate is changing linearly according to the following methods.
 (1)
(1)
R is rate of change of the shear rate (for constant in an experiment), s−1/s; t1 is the time for shear rate rising, s.
Experimental temperature is near the pour point temperature of oils, and rate of change of shear rate is 1.5625 s−1/s, 1.0 s−1/s, 0.5 s−1/s, 0.2 s−1/s, 0.05 s−1/s and 0.025 s−1/s. The time for shear rate rising is 16 s, 25 s, 50 s, 125 s, 500 s and 1000 s. Figure 1 shows hysteresis loop of Zhongyuan crude oil under different shear rate in 34˚C.
3. Thixotropic Models
The thixotropic models in the literature that put forward for studying waxy crude oils, widely applied in the waxy crude oil at present and put forward for blood and being applicable to description of blood hysteresis loop are object of study.
Model 1: This model was originally developed for slurry by Houska but currently widely used for hydraulic analysis of oil pipeline restart [13] - [15] .
Table 1. Properties of crude oils.
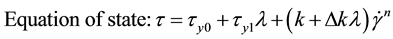 (2)
(2)
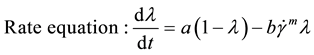 (3)
(3)
where  is the structure parameter, dimensionless;
is the structure parameter, dimensionless; 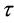 is the shear stress, Pa;
is the shear stress, Pa;  is the shear rate, s−1; t is the shear time, s. τy0 represents the permanent yield stress and τy1 is the thixotropic part of yield stress, which can decay with time. The symbol of a is structure buildup rate constant, while b is structure breakdown rate constant. k, Δk, m, n are all model parameters, unit of the first two is Pa∙sn, the last two are dimensionless.
is the shear rate, s−1; t is the shear time, s. τy0 represents the permanent yield stress and τy1 is the thixotropic part of yield stress, which can decay with time. The symbol of a is structure buildup rate constant, while b is structure breakdown rate constant. k, Δk, m, n are all model parameters, unit of the first two is Pa∙sn, the last two are dimensionless.
In general, all the parameters in the model are determined by fitting experimental data (as well as other models below). Houska model does not consider that structure in limited time is not completely reversible.
Model 2: This model was proposed by Zhao Xiaodong inspired by Cheng’s hypothesis of existence of reversible and irreversible structures in waxy oils [16] and based on Houska Model [17] . It has been proved that it can well describe thixotropic behavior of shear stress attenuation of the waxy crude oil under the condition of constant shear rate [18] [19] .
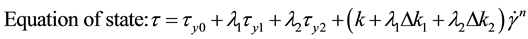 (4)
(4)
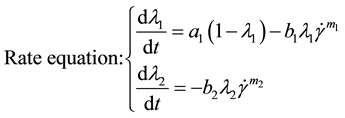 (5)
(5)
where 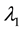 is the structure parameter of recoverable structure, dimensionless.
is the structure parameter of recoverable structure, dimensionless. 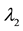 is the structural parameter of unrecoverable structure, dimensionless. τy2 is the thixotropic part of yield stress of recoverable structure, Pa. τy3 is the thixotropic part of yield stress of unrecoverable structure, Pa. a1 is the building rate constant of recoverable structure, s−1; b1 is the cracking rate constant of recoverable structure, sm−1; b2 is the cracking rate constant of unrecoverable structure, sm−1; k, Δk1, Δk2, m1, m2, n are all model parameters, unit of the first three is Pa・sn, the last three are dimensionless.
is the structural parameter of unrecoverable structure, dimensionless. τy2 is the thixotropic part of yield stress of recoverable structure, Pa. τy3 is the thixotropic part of yield stress of unrecoverable structure, Pa. a1 is the building rate constant of recoverable structure, s−1; b1 is the cracking rate constant of recoverable structure, sm−1; b2 is the cracking rate constant of unrecoverable structure, sm−1; k, Δk1, Δk2, m1, m2, n are all model parameters, unit of the first three is Pa・sn, the last three are dimensionless.
Model 3: This model was by Chen Hongjian based on Houska model and the characteristic is that it uses separate structure parameters for the yield stress and the consistency cracking down [20] .
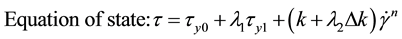 (6)
(6)
 (7)
(7)
where  is the structural parameter of yield stress;
is the structural parameter of yield stress; 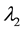 is the structural parameter of consistency; k, Δk, n, a1, a2, b1, b2, m1, m2 are all model parameters. The units are the same as the former ones.
is the structural parameter of consistency; k, Δk, n, a1, a2, b1, b2, m1, m2 are all model parameters. The units are the same as the former ones.
Model 4: This model is proposed by Huang based on statistical mechanics and irreversible thermodynamics principle of state variables entropy. It is derived by introducing a structural arrangement parameter to describe system entropy increase rate caused by structural changes due to the shearing and has been used to describe the hysteresis loop feature of human body blood [21] [22] .
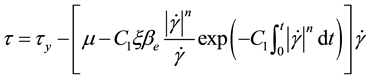 (8)
(8)
where 




Under the experimental condition of hysteresis loop, the expression of the model is shown below.
Uplink:

Downlink:

Model 5: Fang Bo developed this model to describe the hysteresis loop feature of viscoelastic-thixotropic behavior of blood [23] [24] .

where G is the elastic modulus, Pa.
Under the condition of constant shear rate and after integral, the equation is shown below.

For the loading mode of hysteresis loop and after integral, the equation is shown below.
Uplink:

Downlink:

Model 6: This model is proposed by Fang Bo based on the model 5 and has been used to describe hysteresis loop characteristics that reflect viscoelasticity, thixotropy and shear thinning feature of blood [25] .

where K0 is the dissociation rate constant of elastomer, sm−1; m is the parameter of the impact on elastomer dissociation rate of
Under the condition of constant shear rate and after integral, the equation is shown below.

For the loading mode of hysteresis loop and after integral, the equation is shown below.
Uplink:

Downlink:

Model 7: The model proposed by Hou Lei for viscoelastic mechanics analysis of waxy crude oils, has been used to describe the stress attenuation characteristics of Daqing crude oil and Zhongyuan crude oil with the pour-point depressants under the constant shear rate [26] .



where 
Model 8: The model ia proposed by Liu Gang with mechanical analogy principle, which is a viscoelastic- thixotropic mathematical model that liken the gelled crude oil to the physical model that Maxwell body and thixotropic components parallel. It is used to describe the stress attenuation characteristics of the waxy crude oils under constant shear rate [27] . The model only considers the damage that shear gives flocculation body of wax crystal structure in the thixotropic components, but does not take into account recovery of wax crystal structure.

where B is the characteristic parameter associated with the size of wax crystal flocculation body in crude oil, Pa×s; n is the parameter related to structural damage, dimensionless; D is the cracking rate constant of structure, sn−1.
Under the condition of constant shear rate and after integral, the equation is

Among them,
where t1 is the time as the shear rate increases from 0 to a set value, s; k is the linear increase rate as the shear rate increases from 0 to a set value, s−2.
For the loading mode of hysteresis loop and after integral according to the relationship between the shear rate and the time, the equation is shown below.
Uplink:

Downlink:

4. Evaluation of Thixotropic Models
For three kinds of loading modes, the mathematical models above are respectively integrate and dispersed,and experimental data are fitted with the least-squares principle through the computer program, then the model parameter values can be obtained respectively. At the same time the average deviation is used as a statistical index that evaluates the goodness fit of the fitting curve and the experimental data. Here the average deviation is defined as the average value of deviation absolute value between experimental and fitting value.
4 oil samples described in Table 1 are tested under 18 kinds of temperature. Experimental data are fitted with the thixotropic model above respectively for each loading mode, each kind of oil sample and each temperature. Part of the experimental data fitting effect is shown in Figures 1-3. The average deviation results of experimental data of 4 kinds of oil samples under three loading modes are shown in Table 2.


Figure 1. Comparison between experimental data of different shear rates and model regressions for the Zhongyuan crude at 34˚C.


Figure 2. Comparison between experimental data with stepwise increase of shear rate and model regressions for the Daqing crude at 34˚C.



Figure 3. Regressions to multi-loops under various rates of shear rate sweep for the Zhongyuan crude at 34˚C.
The result shows that fitting effect of model 2 is the best for four kinds of waxy crude oils under three kinds of loading modes, which is obviously superior to other models. Fitting effect of model 4 - 6 put forward for thixotropy of human body blood is not good when used to describe hysteresis loop of thixotropy of waxy crude oils. And under the other two loading modes, their fitting effect is also inferior to other models, so they are not suitable for waxy crude oils.
5. Conclusions
With the thixotropy test data of four kinds of waxy crude oils under three kinds of loading modes, feasibility of eight thixotropic models that describe the thixotropy of waxy crude oils in the literature has been evaluated. The
Table 2. The average absolute deviations between predicted data and experimental data.
a. For model 4, only test data of hysteresis loop were fitted.
result shows that:
1) Model 2 with the idea of Cheng that completely reversible and totally irreversible structures both exist in waxy oil products, based on the Houska model and with two structure parameters can well describe three thixotropic behaviors of waxy crudes.
2) Models 4 - 6 put forward for the human body blood thixotropy are not suitable for waxy crudes.
Funding
National Natural Science Foundation of China (No. 51404072).
References
- Li, C.X. (2007) Crude Oil Rheology. Petroleum Industry Press, Beijing, 136-140.
- Mewis, J. and Wagner, N.J. (2009) Thixotropy. Advances in Colloid and Interface Science, 147, 214-227. http://dx.doi.org/10.1016/j.cis.2008.09.005
- Cheng, D.C.-H. (1987) Thixotropy. International Journal of Cosmetic Science, 9, 151-191. http://dx.doi.org/10.1111/j.1467-2494.1987.tb00472.x
- Mewis, J. (1979) Thixotropy―General Review. Journal of Non-Newtonian Fluid Mechanics, 6, 1-20. http://dx.doi.org/10.1016/0377-0257(79)87001-9
- Barnes, H.A. (1997) Thixotropy Review. Journal of Non-Newtonian Fluid Mechanics, 70, 1-33. http://dx.doi.org/10.1016/S0377-0257(97)00004-9
- Dullaert, K. and Mewis, J. (2005) Thixotropy: Build-Up and Breakdown Curves during Flow. Journal of Rheology, 6, 1213-1230. http://dx.doi.org/10.1122/1.2039868
- Dullaert, K. and Mewis, J. (2006) A Structural Kinetics Model for Thixotropy. Journal of Non-Newtonian Fluid Mechanics, 139, 21-30. http://dx.doi.org/10.1016/j.jnnfm.2006.06.002
- Huang, C.R. (1972) A Thermodynamic Approach to Generalised Rheological Equations of State for Time-Dependent and Time-Independent Non-Newtonian Fluids. The Chemical Engineering Journal, 3, 100-104. http://dx.doi.org/10.1016/0300-9467(72)85011-1
- Li, H., Zhang, X.M. and Zhang, S.H. (2000) SY/T 7550-2000 Petroleum and Natural Gas Industries Standard of The People’s Republic of China―Determination of Wax, Resins and Asphaltenes Contents in Crude Oil. Petroleum industry Press, Beijing.
- Shi, J., Quan, Z.Y. and Cheng, P.J. (1995) SY/T 0545-1995 Petroleum and Natural Gas Industries Standard of the People’s Republic of China-Determination of Thermal Characteristics Related to Wax Precipitation of Oil―Differen- tial Scanning Calorimetry. Petroleum Industry Press, Beijing.
- Luo, Z.M., Li, C.X. and Zhao M.X. (1994) SY/T 0541-1994 Petroleum and Natural Gas Industries Standard of The People’s Republic of China-Determination of Crude Freezing Point. Petroleum Industry Press, Beijing.
- Zhu, G.Y., Hua, H.Z. and Guan, H.Z. (1984) GB1884-1983 Petroleum and Natural Gas Industries Standard of The People’s Republic of China―Oil and Liquid Petroleum Products Density Measuremen. Petroleum Industry Press, Beijing.
- Houska, M. (1981) Engineering Aspects of the Rheology of Thixotrpic Liquids. PhD Thesis, Czech Technical University of Prague, Prague.
- Wachs, A., Vinay, G. and Frigaard, I. (2009) A 1.5D Numerical Model for the Start Up of Weakly Compressible Flow of Aviscoplastic and Thixotropic Fluid in Pipelines. Journal of Non-Newtonian Fluid Mech, 2, 1-53.
- Sestak, J., Charles, M.E. and Cawkwell, M.G. (1987) Start-Up of Gelled Crude Oil Pipeline. Journal of Pipelines, 6, 15-24.
- Cheng, D.C-H. (1986) Yield Stress: A Time Dependent Property and How to Measure It. Rheologica Acta, 25, 542- 554. http://dx.doi.org/10.1007/BF01774406
- Zhao, X.D. (1999) Study on Unsteady Hydraulic and Thermodynamic Calculation Method of the Modified Crude Oil Pipeline Restarting. PhD Thesis, University of Petroleum, Beijing.
- Zhang, F., Zhang, J.J. and Yang, X.J. (2004) Comparison of Thixotropic Models of Waxy Crude Oil: Proceedings of the XIV International Congress on Rheology. PhD Thesis, Korea Society of Rheology, Seoul.
- Ma, W.P., Qi, H.S. and Peng, S.Y. (2008) Experimental Research on Thixotropic Characteristic of Daqing Crude Oil Blended with Russian Crude Oil. Oil and Gas Storage and Transportation, 27, 27-32.
- Chen, H.J. (2002) The Restarting Pressure Research of a Crude Pipeline. PhD Thesis, University of Petroleum, Beijing.
- Huang, C.R. (1972) A Thermodynamic Approach to Generalized Rheological Equations of State for Time-Dependent and Time-Independent Non-Newtonian Fluids. The Chemical Engineering Journal, 3, 100-104. http://dx.doi.org/10.1016/0300-9467(72)85011-1
- Huang, C.R. and Fabisiak, W. (1978) A Rheological Equation Characterizing Both the Time Dependent and the Steady State Viscosity of Whole Human Blood. American Institute of Chemical Engineers―Symposium Series, 74, 19-21.
- Fang, B., Jin, H. and Jiang, T.Q. (1999) Study on Constitutive Equation of Blood Hysteresis Loop (I): Hysteresis Loop Constitutive Equation of Reflecting Viscoelasticity and Thixotropy. The 6th National Conference on Rheology, Center China University of Science and Technology Press, Wuhan.
- Fang, B. and Jiang, T.Q. (1998) Mathematical Charaterization of Blood Viscoelasticity and Thixotropy Studies on the Novel 5-Paramater Time-Dependent Constitutive Equation and Its Suitability. Journal of East China University of Science and Technology, 24, 393-398.
- Fang, B., Song, D.Y. and Jiang, T.Q. (1999) Study on the Novel 7-Parameter Constitutive Equation for Viscoelastic- Thixotropic Fluids. Advances in Rheology. The 6th National Conference on Rheology, Center China University of Science and Technology Press, Wuhan.
- Hou, L. and Zhang, J.J. (2005) Study on Thixotropy of Waxy Crude Based on Viscoelasticity Analysis. Journal of the University of Petroleum, China (Natural Science), 29, 84-94.
- Liu, G., Zhang, G.Z. and Deng, Y. (2003) Viscoelasticity-Thixotropy Constitutive Equation for Gelled Crude Oil. Journal of the University of Petroleum, China (Natural Science), 27, 72-75.












