Open Journal of Discrete Mathematics
Vol.1 No.2(2011), Article ID:5808,6 pages DOI:10.4236/ojdm.2011.12012
Word-Representability of Line Graphs*
1School of Computer Science, Reykjavik University, Reykjavik, Iceland
2Department of Theoretical Cybernetics, Sobolev Institute of Mathematics, Novosibirsk, Russia
3Department of Computer and Information Sciences, University of Strathclyde, Glasgow, UK
E-mail: sergey.kitaev@gmail.com
Received April 18, 2011; revised May 17, 2011; accepted June 3, 2011
Keywords: line graph, representability by words, wheel, complete graph
Abstract
A graph  is representable if there exists a word
is representable if there exists a word  over the alphabet
over the alphabet  such that letters
such that letters  and
and  alternate in
alternate in  if and only if
if and only if  is in
is in  for each
for each  not equal to
not equal to . The motivation to study representable graphs came from algebra, but this subject is interesting from graph theoretical, computer science, and combinatorics on words points of view. In this paper, we prove that for
. The motivation to study representable graphs came from algebra, but this subject is interesting from graph theoretical, computer science, and combinatorics on words points of view. In this paper, we prove that for  greater than 3, the line graph of an
greater than 3, the line graph of an  -wheel is non-representable. This not only provides a new construction of non-representable graphs, but also answers an open question on representability of the line graph of the 5-wheel, the minimal non-representable graph. Moreover, we show that for
-wheel is non-representable. This not only provides a new construction of non-representable graphs, but also answers an open question on representability of the line graph of the 5-wheel, the minimal non-representable graph. Moreover, we show that for  greater than 4, the line graph of the complete graph is also non-representable. We then use these facts to prove that given a graph
greater than 4, the line graph of the complete graph is also non-representable. We then use these facts to prove that given a graph  which is not a cycle, a path or a claw graph, the graph obtained by taking the line graph of
which is not a cycle, a path or a claw graph, the graph obtained by taking the line graph of 
 -times is guaranteed to be non-representable for
-times is guaranteed to be non-representable for  greater than 3.
greater than 3.
1. Introduction
A graph  is representable if there exists a word
is representable if there exists a word  over the alphabet
over the alphabet  such that letters
such that letters  and
and  alternate in
alternate in  if and only if
if and only if  for each
for each . Such a
. Such a  is called a word-representant of
is called a word-representant of . Note that in this paper we use the term graph to mean a finite, simple graph, even though the definition of representable is applicable to more general graphs.
. Note that in this paper we use the term graph to mean a finite, simple graph, even though the definition of representable is applicable to more general graphs.
It was shown by Kitaev and Pyatkin, in [1], that if a graph is representable by , then one can assume that
, then one can assume that  is uniform, that is, it contains the same number of copies of each letter. If the number of copies of each letter in
is uniform, that is, it contains the same number of copies of each letter. If the number of copies of each letter in  is
is , we say that
, we say that  is
is  -uniform. For example, the graph to the left in Figure 1 can be represented by the 2-uniform word 12312434 (in this word every pair of letters alternate, except 1 and 4, and 2 and 4), while the graph to the right, the Petersen graph, can be represented by the 3-uniform word
-uniform. For example, the graph to the left in Figure 1 can be represented by the 2-uniform word 12312434 (in this word every pair of letters alternate, except 1 and 4, and 2 and 4), while the graph to the right, the Petersen graph, can be represented by the 3-uniform word  (the Petersen graph cannot be represented by a 2-uniform word as shown in [2])
(the Petersen graph cannot be represented by a 2-uniform word as shown in [2])
The notion of a representable graph comes from algebra, where it was used by Kitaev and Seif to study the growth of the free spectrum of the well known Perkins semigroup [3]. There are also connections between representable graphs and robotic scheduling as described by Graham and Zang in [4]. Moreover, representable graphs are a generalization of circle graphs, which was shown by Halldórsson, Kitaev and Pyatkin in [5], and thus they are interesting from a graph theoretical point of view. Finally, representable graphs are interesting from a combinatorics on words point of view as they deal with the study of alternations in words.
Not all graphs are representable. Examples of minimal (with respect to the number of nodes) non-representable graphs given by Kitaev and Pyatkin in [1] are presented in Figure 2.
It was remarked in [5] that very little is known about the effect of the line graph operation on the representability of a graph. We attempt to shed some light on this subject by showing that the line graph of the smallest

Figure 1. A graph representable by a 2-uniform word and the Petersen graph.

Figure 2. Minimal non-representable graphs.
known non-representable graph, the wheel on five vertices,  , is in fact non-representable. In fact we prove a stronger result, which is that
, is in fact non-representable. In fact we prove a stronger result, which is that  (where
(where  denotes the line graph of
denotes the line graph of ) is non-representable for
) is non-representable for . From the non-representability of
. From the non-representability of  we are led to a more general theorem regarding line graphs. Our main result is that
we are led to a more general theorem regarding line graphs. Our main result is that , where
, where  is not a cycle, a path or the claw graph, is guaranteed to be non-representable for
is not a cycle, a path or the claw graph, is guaranteed to be non-representable for .
.
Although almost all graphs are non-representable (as discussed in [1]) and even though a criteria in terms of semi-transitive orientations is given in [5] for a graph to be representable, essentially only two explicit constructions of non-representable graphs are known. Apart from the so-called  graph whose non-representability is proved in [2] in connection with solving an open problem in [1], the known constructions of non-representable graphs can be described as follows. Note that the property of being representable is hereditary, i.e., it is inherited by all induced subgraphs, thus adding additional nodes to a non-representable graph and connecting them in an arbitrary way to the original nodes will also result in a non-representable graph.
graph whose non-representability is proved in [2] in connection with solving an open problem in [1], the known constructions of non-representable graphs can be described as follows. Note that the property of being representable is hereditary, i.e., it is inherited by all induced subgraphs, thus adding additional nodes to a non-representable graph and connecting them in an arbitrary way to the original nodes will also result in a non-representable graph.
• Adding an all-adjacent node to a non-comparability graph results in a non-representable graph (all of the graphs in Figure 2 are obtained in this way). This construction is discussed in [1].
• Let  be a 4-chromatic graph with girth (the length of the shortest cycle) at least 10 (such graphs exist by a theorem of Erdös). For every path of length 3 in
be a 4-chromatic graph with girth (the length of the shortest cycle) at least 10 (such graphs exist by a theorem of Erdös). For every path of length 3 in  add a new edge connecting the ends of the path. The resulting graph will be non-representable as shown in [5]. This construction gives an example of trianglefree non-representable graphs whose existence was asked for in [1].
add a new edge connecting the ends of the path. The resulting graph will be non-representable as shown in [5]. This construction gives an example of trianglefree non-representable graphs whose existence was asked for in [1].
Our results showing that ,
,  , and
, and ,
,  , are non-representable give two new constructions of non-representable graphs.
, are non-representable give two new constructions of non-representable graphs.
Our main result about repeatedly taking the line graph, shown in Section 5, also gives a new method for constructing non-representable graphs when starting with an arbitrary graph (excluding cycles, paths and the claw graph of course). Since we can start with an arbitrary graph this should also allow one to construct non-representable graphs with desired properties by careful selection of the original graph.
Although we have answered some questions about the line graph operation, there are still open questions related to the representability of the line graph, and in Sect. 6 we list some of these problems.
2. Preliminaries on Words and Basic Observations
2.1. Introduction to Words
We denote the set of finite words on an alphabet  by
by  and the empty word by
and the empty word by .
.
A morphism  is a mapping
is a mapping  that satisfies the property
that satisfies the property  for all words
for all words ,
, . Clearly, the morphism is completely defined by its action on the letters of the alphabet. The erasing of a set
. Clearly, the morphism is completely defined by its action on the letters of the alphabet. The erasing of a set  of symbols is a morphism
of symbols is a morphism  such that
such that  if
if  and
and  otherwise.
otherwise.
A word  occurs in a word
occurs in a word  at the position
at the position  and is called a subword of
and is called a subword of  if
if  for some
for some ,
, . A subword that occurs at position 0 in some word is called a prefix of that word. A word is
. A subword that occurs at position 0 in some word is called a prefix of that word. A word is  -uniform if each symbol occurs in it exactly
-uniform if each symbol occurs in it exactly  times. We say that a word is uniform if it is
times. We say that a word is uniform if it is  -uniform for some
-uniform for some .
.
Symbols ,
,  alternate in a word
alternate in a word  if both of them occur in
if both of them occur in  and after erasing all other letters in
and after erasing all other letters in  we get a subword of
we get a subword of .
.
The alternating graph  of a word
of a word  is a graph on the symbols occurring in
is a graph on the symbols occurring in  such that
such that  has an edge
has an edge  if and only if
if and only if ,
,  alternate in
alternate in . A graph
. A graph  is representable if it is the alternating graph of some word
is representable if it is the alternating graph of some word . We call
. We call  a representant of
a representant of  in this case.
in this case.
A key property of representable graphs was shown by Kitaev and Pyatkin in [1]:
Theorem 1 Each representable graph has a uniform representant.
Assuming uniformity makes dealing with the representant of a graph a much nicer task and plays a crucial role in some of our proofs.
2.2. Basic Observations
A cyclic shift of a word  is the word
is the word .
.
Proposition 2 Uniform words  and
and  have the same alternating graph.
have the same alternating graph.
Proof. Alternating relations of letters not equal to  are not affected by the cyclic shift. Thus we need only to prove that
are not affected by the cyclic shift. Thus we need only to prove that  has the same alternating relations with other symbols in
has the same alternating relations with other symbols in  as it had in
as it had in .
.
Suppose ,
,  alternate in
alternate in . Due to
. Due to  being uniform, it must be that
being uniform, it must be that , where
, where  is the uniform number of
is the uniform number of . In this case,
. In this case, and hence the symbols
and hence the symbols ,
, alternate in
alternate in .
.
Suppose ,
,  do not alternate
do not alternate . Since
. Since  is uniform,
is uniform,  is a subword of
is a subword of . Also, we know that
. Also, we know that  cannot be the prefix of
cannot be the prefix of , so it must occur in
, so it must occur in too. Hence,
too. Hence,  ,
,  do not alternate in
do not alternate in .
.
Taking into account this fact, we may consider representants as cyclic or infinite words in order not to treat differently the end of the word while considering a local part of it.
Let us denote a clique on  vertices by
vertices by . One can easily prove the following proposition.
. One can easily prove the following proposition.
Proposition 3 An  -uniform word that is a representant of
-uniform word that is a representant of  is a word of the form
is a word of the form  where
where  is 1-uniform word containing
is 1-uniform word containing  letters.
letters.
Let us consider another simple case, the cycle  on
on  vertices.
vertices.
Lemma 4 The word  is not a subword of any uniform representant of
is not a subword of any uniform representant of  with vertices labeled in consecutive order, where
with vertices labeled in consecutive order, where .
.
Proof. Suppose,  is a uniform representant of
is a uniform representant of  and
and  is a subword of
is a subword of . Due to Proposition 2 we may assume that
. Due to Proposition 2 we may assume that  is a prefix of
is a prefix of . Define
. Define  to be the position of the
to be the position of the  -th instance of
-th instance of  in
in  for
for . Now for all adjacent vertices
. Now for all adjacent vertices  we have
we have  for each
for each .
.
Vertices 0, 2 are not adjacent in  and so do not alternate in
and so do not alternate in . It follows that there is a
. It follows that there is a 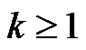 such that
such that  or
or .
.
Suppose . Since
. Since ,
, and
and ,
, are adjacent, we have
are adjacent, we have  and
and  for each
for each . Then we have a contradiction
. Then we have a contradiction .
.
Suppose . Since all pairs
. Since all pairs  and the pair
and the pair  are adjacent, we have inequalities
are adjacent, we have inequalities  for each
for each ,
,  , and
, and  for each
for each . Thus we get a contradiction
. Thus we get a contradiction  .
.
Here we introduce some notation. Let  be a representant of some graph
be a representant of some graph  that contains a set of vertices
that contains a set of vertices  such that
such that  and
and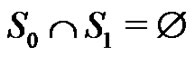 . We use the notation
. We use the notation  for the statement “Between every two consecutive occurrences of
for the statement “Between every two consecutive occurrences of  in
in , for every
, for every , each symbol of
, each symbol of  occurs once and each symbol of
occurs once and each symbol of  occurs before any symbol of
occurs before any symbol of ” and the notation
” and the notation  for the statement “There are two consecutive occurrences of
for the statement “There are two consecutive occurrences of  in
in , for at least one
, for at least one , such that each symbol of
, such that each symbol of  occurs between them and each symbol of
occurs between them and each symbol of  occurs before any symbol of
occurs before any symbol of ” Note that
” Note that  implies
implies  and is contrary for
and is contrary for . The quantifiers in these statements operate on pairs of consecutive occurrences of
. The quantifiers in these statements operate on pairs of consecutive occurrences of  in all cyclic shifts of the given representant. This notation may be generalized to an arbitrary number of sets
in all cyclic shifts of the given representant. This notation may be generalized to an arbitrary number of sets  with the same interpretation.
with the same interpretation.
The following proposition illustrates the use of this notation.
Proposition 5 Let a word  be a representant of some graph
be a representant of some graph  containing vertices
containing vertices , where
, where  and
and  are adjacent. Then we have
are adjacent. Then we have
1)  being not adjacent implies that both of the statements
being not adjacent implies that both of the statements ,
,  are true for
are true for
2)  being adjacent implies that exactly one of the statements
being adjacent implies that exactly one of the statements ,
,  is true for
is true for .
.
Proof. (Case 1) Since  and
and  alternate, at least one of
alternate, at least one of ,
,  is true. If only one of them is true for
is true. If only one of them is true for , then
, then  alternate in it, which is a contradiction with
alternate in it, which is a contradiction with  being not adjacent.
being not adjacent.
(Case 2) the statement follows immediately from Proposition 3.
3. Line Graphs of Wheels
The wheel graph, denoted by , is a graph we obtain from a cycle
, is a graph we obtain from a cycle  by adding one external vertex adjacent to every other vertex.
by adding one external vertex adjacent to every other vertex.
A line graph  of a graph
of a graph  is a graph on the set of edges of
is a graph on the set of edges of  such that in
such that in  there is an edge
there is an edge  if and only if edges
if and only if edges  are adjacent in
are adjacent in .
.
Theorem 6 The line graph  is not representable for each
is not representable for each .
.
Proof. Let us describe  first. Denote edges of the big (external) cycle of the wheel
first. Denote edges of the big (external) cycle of the wheel  by
by  in consecutive order and internal edges that connect the inside vertex to the big cycle by
in consecutive order and internal edges that connect the inside vertex to the big cycle by  so that an edge
so that an edge  is adjacent to
is adjacent to  and
and  for
for  and
and  is adjacent to
is adjacent to ,
, .
.
In the line graph  the vertices
the vertices  form a cycle where they occur consecutively and the vertices
form a cycle where they occur consecutively and the vertices  form a clique. In addition, vertices
form a clique. In addition, vertices  are adjacent to
are adjacent to ,
,  and
and  is adjacent to
is adjacent to ,
, .
.
Suppose that  is the alternating graph of some word that, due to Theorem 1, can be chosen to be uniform. Now we deduce a contradiction with Lemma 4.
is the alternating graph of some word that, due to Theorem 1, can be chosen to be uniform. Now we deduce a contradiction with Lemma 4.
Let  be the alphabet
be the alphabet ,
,  be the alphabet
be the alphabet  and a word
and a word 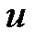 on the alphabet
on the alphabet  be the uniform representant of
be the uniform representant of . Due to Proposition 2, we may assume
. Due to Proposition 2, we may assume .
.
As we know from Proposition 3, the word  is of the form
is of the form , where
, where  is 1-uniform and
is 1-uniform and . Let us prove that
. Let us prove that  is exactly
is exactly  or
or .
.
Suppose there are some  such that
such that . Note, that
. Note, that  due to
due to  being 1-uniform. The supposition implies that the statement
being 1-uniform. The supposition implies that the statement  is true for
is true for . The vertex
. The vertex  is neither adjacent to
is neither adjacent to  nor to
nor to . By Proposition 5 this implies
. By Proposition 5 this implies  and
and  are true for
are true for . Taking into account the previous “for all” statement, we conclude that both of
. Taking into account the previous “for all” statement, we conclude that both of  and
and  are true for
are true for , which contradicts Proposition 5 applied to
, which contradicts Proposition 5 applied to . So, there are only two possible cases, i.e.,
. So, there are only two possible cases, i.e.,  and
and .
.
Using the same reasoning on a triple ,
,  ,
,  , by induction on
, by induction on , we get
, we get  for the first case and
for the first case and  for the second.
for the second.
It is sufficient to prove the theorem only for the first case, since reversing a word preserves the alternating relation.
By Proposition 5 exactly one of the statements ,
,  is true for
is true for . Let us prove that it is the statement
. Let us prove that it is the statement .
.
Applying Proposition 5 to the clique  we have that exactly one of
we have that exactly one of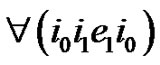 ,
,  is true. Applying Proposition 5 to
is true. Applying Proposition 5 to  we have that both of
we have that both of  and
and  are true. The statement
are true. The statement  contradicts
contradicts  since we have
since we have  . Hence
. Hence  is true.
is true.
Now applying Proposition 5 to ,
,  and
and  we have
we have . Taking into account
. Taking into account  and Proposition 5 applied to the clique
and Proposition 5 applied to the clique  we conclude that
we conclude that  is true. In other words, between two consecutive
is true. In other words, between two consecutive  in
in  there is
there is  that occurs before
that occurs before .
.
Using the same reasoning, one can prove that the statement  and the statements
and the statements  for each
for each  are true for
are true for . Let us denote this set of statements by (*).
. Let us denote this set of statements by (*).

Figure 3.The wheel graph W5 and its line graph.
The vertex  is not adjacent to the vertex
is not adjacent to the vertex  but both of them are adjacent to
but both of them are adjacent to , hence, by Proposition 5somewhere in
, hence, by Proposition 5somewhere in  the word
the word  occurs.
occurs.
Taking into account what we have already proved for , this means that we found the structure
, this means that we found the structure  in
in , where symbols of
, where symbols of  do not occur in gaps denoted by “
do not occur in gaps denoted by “ ”.
”.
Now inductively applying the statements (*), we conclude that in  there is a structure
there is a structure  where no symbol
where no symbol 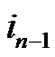 occurs in the gaps. Suppose the symbol
occurs in the gaps. Suppose the symbol  occurs somewhere in the gaps between
occurs somewhere in the gaps between  and
and . Since
. Since  and
and 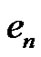 are adjacent, that would mean that between two
are adjacent, that would mean that between two  another
another  also occurs and this contradicts the fact that
also occurs and this contradicts the fact that  and
and  are adjacent. One may prove that no symbol of
are adjacent. One may prove that no symbol of  occurs in the gaps between
occurs in the gaps between  and
and  in the structure we found, by using induction and arriving at a contradiction similar to the one above. In other words,
in the structure we found, by using induction and arriving at a contradiction similar to the one above. In other words,  occurs in the word
occurs in the word  representing the cycle. This results in a contradiction with Lemma 4 which concludes the proof.
representing the cycle. This results in a contradiction with Lemma 4 which concludes the proof.
4. Line Graphs of Cliques
Theorem 7 The line graph  is not representable for each
is not representable for each .
.
Proof. It is sufficient to prove the theorem for the case  since, as one can prove, any
since, as one can prove, any  contains an induced
contains an induced .
.
Let  be a representant of
be a representant of  with its vertices labeled as shown in Figure 4. Vertices
with its vertices labeled as shown in Figure 4. Vertices  make a clique in
make a clique in . By applying Propositions 3 and 5 to this clique we see that exactly one of the following statements is true:
. By applying Propositions 3 and 5 to this clique we see that exactly one of the following statements is true: ,
,  ,
,  , where
, where  and
and  is the negation of
is the negation of .
.
(Case 1) Suppose  is true. The vertex 3 is adjacent to
is true. The vertex 3 is adjacent to ,
,  , but not to 0, 1. Keeping in mind that
, but not to 0, 1. Keeping in mind that  is also adjacent to 0 and 1, then applying Proposition 5 we have that
is also adjacent to 0 and 1, then applying Proposition 5 we have that  and
and  are true. But between
are true. But between ,
,  there is
there is , so we have a contradiction
, so we have a contradiction ,
,  with Proposition 5.
with Proposition 5.
(Case 2a) Suppose  is true. The vertex
is true. The vertex  is adjacent with
is adjacent with , 0, but not with
, 0, but not with , 1. Applying Proposition 5 we have
, 1. Applying Proposition 5 we have  and
and . Taking into account the case condition, this implies
. Taking into account the case condition, this implies  and
and  which is a contradiction.
which is a contradiction.
(Case 2b) Suppose  is true. The vertex 2 is adjacent with
is true. The vertex 2 is adjacent with , 1, but not with
, 1, but not with , 0. Applying Proposition 5 we have
, 0. Applying Proposition 5 we have  and
and . Again, taking into account the case condition this implies
. Again, taking into account the case condition this implies  and
and , which gives a contradiction.
, which gives a contradiction.
(Case 3a) If  is true, a contradiction follows analogously to Case 2b.
is true, a contradiction follows analogously to Case 2b.
(Case 3b) If  is true, a contradiction follows analogously to Case 2a.
is true, a contradiction follows analogously to Case 2a.
5. Iterating the Line Graph Construction
It was shown by van Rooji and Wilf [6] that iterating the line graph operator on most graphs results in a sequence of graphs which grow without bound. The exceptions are cycles, which stay as cycles of the same length, the claw graph , which becomes a triangle after one iteration and then stays that way, and paths, which shrink to the empty graph. This unbounded growth results in graphs that are non-representable after a small number of iterations of the line graph operator since they contain the line graph of a large enough clique. A slight modification of this idea is used to prove our main result.
, which becomes a triangle after one iteration and then stays that way, and paths, which shrink to the empty graph. This unbounded growth results in graphs that are non-representable after a small number of iterations of the line graph operator since they contain the line graph of a large enough clique. A slight modification of this idea is used to prove our main result.
Theorem 8 If a connected graph  is not a path, a cycle, or the claw graph
is not a path, a cycle, or the claw graph , then
, then  is not representable for
is not representable for .
.
Proof. Note that if  appears as a subgraph of
appears as a subgraph of  (not necessarily induced), then
(not necessarily induced), then 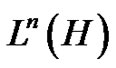 is isomorphic to
is isomorphic to

Figure 4. The clique K5 and its line graph, where edges mentioned in the proof of Theorem 4 are drawn thicker.

Figure 5. Iterating the line graph construction.
an induced subgraph of  for all
for all .
.
We first consider the sequence of graphs in Figure 5. All but the leftmost graph are obtained by applying the line graph operator to the previous graph. The last graph in the sequence is , and by Theorem 6,
, and by Theorem 6,  is non-representable.
is non-representable.
Now, let  be a graph that is not a star and that satisfies the conditions of the theorem.
be a graph that is not a star and that satisfies the conditions of the theorem.  contains as a subgraph an isomorphic copy of either the leftmost graph of Figure 5 or the second graph from the left. Thus
contains as a subgraph an isomorphic copy of either the leftmost graph of Figure 5 or the second graph from the left. Thus , or respectively
, or respectively , is not representable, since it contains an induced line graph of the wheel
, is not representable, since it contains an induced line graph of the wheel .
.
If  is a star
is a star  then
then  is the clique
is the clique  and there is an isomorphic copy of the second from the left graph of Figure 5 in
and there is an isomorphic copy of the second from the left graph of Figure 5 in , and
, and  is not representable again.
is not representable again.
Note that there is an isomorphic copy of the second graph of Figure 5 inside the third one. Therefore the same reasoning can be used for  for each
for each , which concludes the proof.
, which concludes the proof.
6. Some Open Problems
We have the following open questions.
• Is the line graph of a non-representable graph always non-representable?
Our Theorem 8 shows that for any graph , that is not a path, a cycle, or the claw
, that is not a path, a cycle, or the claw , the graph
, the graph  is non-representable for all
is non-representable for all . It might be possible to find a graph
. It might be possible to find a graph  such that
such that  is non-representable while
is non-representable while  is.
is.
• How many graphs on  vertices stay non-representable after at most
vertices stay non-representable after at most  iterations,
iterations, ?
?
For a graph  define
define  as the smallest integer such that
as the smallest integer such that  is non-representable for all
is non-representable for all . Theorem 8 shows that
. Theorem 8 shows that  is at most 4, for a graph that is not a path, a cycle, nor the claw
is at most 4, for a graph that is not a path, a cycle, nor the claw , while paths, cycles and the claw have
, while paths, cycles and the claw have .
.
• Is there a finite classification of prohibited subgraphs in a graph  determining whether
determining whether  is representable?
is representable?
There is a classification of prohibited induced subgraphs which determine whether a graph  is the line graph of some other graph
is the line graph of some other graph . It would be nice to have such a classification, if one exists, to determine if
. It would be nice to have such a classification, if one exists, to determine if  is representable.
is representable.
7. References
[1] S. Kitaev and A. Pyatkin, “On Representable Graphs,” Journal of Automata, Languages and Combinatorics, Vol. 13, No. 1, 2008, pp. 45-54.
[2] M. M. Halldórsson, S. Kitaev and A. Pyatkin, “Graphs Capturing Alternations in Words,” In Proceedings of the 14th International Conference on Developments in Language Theory, London, 17-20 August 2010, pp. 436-437.
[3] S. Kitaev and S. Seif, “Word Problem of the Perkins Semigroup via Directed Acyclic Graphs,” Order, Vol. 25, No. 3, 2008, pp. 177-194. doi:10.1007/s11083-008-9083-7
[4] R. Graham and N. Zang, “Enumerating Split-Pair Arrangements,” Journal of Combinatorial Theory, Series A, Vol. 115, No. 2, 2008, pp. 293-303. doi:10.1016/j.jcta.2007.06.003
[5] M. M. Halldorsson, S. Kitaev and A. Pyatkin, “On Representable Graphs, Semi-transitive Orientations, and the Representation Numbers,” Submitted on 1 October 2008. http://arxiv.org/abs/0810.0310v1
[6] A. C. M. van Rooji and H. S. Wilf, “The Interchange Graph of a Finite Graph,” Acta Mathematica Academiae Scientiarum Hungaricae, Vol. 16, No. 3-4, 1965, pp.263- 269. doi:10.1007/BF01904834
NOTES
*Supported by a grant from Iceland, Liechtenstein and Norway through the EEA Financial Mechanism. †Supported and coordinated by Universidad Complutense de Madrid. Supported by the Russian Foundation for Basic Research grants no. 10-01-00616, 11-01-00997 and by the Icelandic Research Fund grant no. 090038013. ‡Supported by grant no. 090038012 from the Icelandic Research Fund. §Supported by grant no. 090038011 from the Icelandic Research Fund.

