 Applied Mathematics, 2011, 2, 1196-1203 doi:10.4236/am.2011.210166 Published Online October 2011 (http://www.SciRP.org/journal/am) Copyright © 2011 SciRes. AM Self-Similar Solution of Heat and Mass Transfer of Unsteady Mixed Convection Flow on a Rotating Cone Embedded in a Porous Medium Saturated with a Rotating Fluid Saleh M. Al-Harbi Department of Mathematics, Makkah Teacher College, Makkah, Saudi Arabia E-mail: salharbi434@yahoo.com Received June 6, 2011; revised August 22, 2011; accepted August 29, 2011 Abstract A self-similar solution of unsteady mixed convection flow on a rotating cone embedded in a porous medium saturated with a rotating fluid in the presence of the first and second orders resistances has been obtained. It has been shown that a self-similar solution is possible when the free stream angular velocity and the angular velocity of the cone vary inversely as a linear function of time. The system of ordinary differential equations governing the flow has been solved numerically using an implicit finite difference scheme in combination with the quasi-linearization technique. Both prescribe wall temperature and prescribed heat flux conditions are considered. Numerical results are reported for the skin friction coefficients, Nusselt number and Sher- wood number. The effect of various parameters on the velocity, temperature and concentration profiles are also presented here. Keywords: Unsteady Mixed Convection, Heat and Mass Transfer, Rotating Cone, Rotating Fluid, Porous Media, Self-Similar Solution 1. Introduction The study and analysis of heat and mass transfer in po- rous media has been the subject of many investigations due to their frequent occurrence in industrial and tech- nological applications. Examples of some applications include geothermal reservoirs, drying of porous solids, thermal insulation, enhanced oil recovery and many oth- ers. Cone–shaped bodies are often encountered in many engineering applications and the heat transfer problem of mixed convection boundary layer flow over a rotating cone, which occurs in rotating heat exchangers, are ex- tensively used by the chemical and automobile industries. Moreover, convective heat on a rotating cone has several important applications such as design of canisters for nuclear waste disposal, nuclear reactor cooling system, geothermal reservoirs. Earlier investigations of flow and heat transfer in rotating systems are given by Hartnett and Deland [1], Hering and Grosh [2] and Tien and Tsuji [3]. Hering and Grosh [4] have obtained a number of similarity solutions for cones with prescribed wall tem- perature being a power function of the distance from the apex along the generator. Himasekhar et al. [5] found the similarity solution of the mixed convection flow over a vertical rotating cone in an ambient fluid for a wide range of Prandtl numbers. Wang [6] has also obtained a similarity solution of boundary layer flows on rotating cones, discs and axisymmetric bodies with concentrated heat sources. Further, Yih [7] has presented non-similar solutions to study the heat transfer characteristics in mixed convection about a cone in saturated porous media. The effect of thermal radiation on the non-Darcy natural convection flow over a vertical cone and wedge embed- ded in a porous medium with variable viscosity and wall mass flux was investigated numerically by EL-Harby [8]. All these studies pertain to steady flows. There is a large body of literature on unsteady, bound- ary-layer flows past bodies of different geometries em- bedded in porous media. Takhar et al. [9] have presented a study on unsteady mixed convection flow over a verti- cal cone rotating in an ambient fluid with a time-de- pendent angular velocity in the presence of a magnetic  S. M. AL-HARBI 1197 field. Therefore, as a step towards the eventual develop- ment of studies on unsteady mixed convection flows, it is interesting as well as useful to investigate the combined effects of thermal and mass diffusion on a rotating cone in a rotating viscous fluid where the angular velocity of the cone and the free stream angular velocity vary arbi- trarily with time. The problem of unsteady mixed con- vection flow on a rotating cone in a rotating fluid has been considered by Anilkumar and Roy [10]. The inter- ested reader can find an excellent collection of papers on unsteady convective flow problems over heated bodies embedded in a fluid-saturated porous medium in the book papers by Pop and Ingham [11] and in the book by Nield and Bejan [12]. Hassanien et al. [13] have studied the unsteady free convection flow in the stagnation-point region of a rotating sphere embedded in a porous me- dium. Also, the problem of unsteady free convection flow in the stagnation-point region of a three-dimensional body embedded in a porous media has been studied by Hassanien et al. [14]. Recently, the problem of unsteady MHD free convection flow past a semi infinite vertical permeable moving plate with heat source and suction has been studied by Ibrahim et al. [15]. Roy et al. [16] have obtained Non-similar solution of an unsteady mixed convection flow over a vertical cone in the presence of surface mass transfer. The effect of combined viscous dissipation and Joule heating on unsteady mixed conven- tion magnetohydrodynamics (MHD) flow on a rotating cone in an electrically conducting rotating fluid in the presence of Hall and ion-slip currents was investigated by Osalusi et al. [17]. The aim of the present paper is to develop a new self–similarity solutions for the heat and mass transfer of unsteady mixed convection flow on a rotating cone em- bedded in a porous medium saturated with a rotating fluid in the presence of the first and second orders resis- tances which to the best of our knowledge have not been investigated yet. The system of ordinary differential equations governing the flow has been solved numeri- cally using the method of an implicit finite difference scheme. 2. Mathematical Analysis We consider the unsteady laminar viscous incompressi- ble fluid flowing over an infinite rotating cone in a rotat- ing fluid–saturated porous medium. Both the cone and the fluid are rotating about the axis of the cone with time-dependent angular velocities either in the same di- rection or in the opposite direction. This introduces un- steadiness in the flow field. We have taken the rectangu- lar co-ordinate system (x, y, z) where x is measured along a meridian section, the y-axis along a circular section and z-axis normal to the cone surface as shown in Figure 1. Let u, v and w be the velocity components along x (tan- gential), y (circumferential) and z (normal) directions, respectively. The buoyancy forces arise due to the temperature and concentration variations in the fluid and the flow is taken to be axi-symmetric. The wall and the free stream are maintained at a constant temperature and concentration. Under the above assumptions and using the Boussinesq approximation, the governing boundary layer momentum, energy and diffusion equation can be expressed as: 0, xu xw xz (1) 2 22 2 2 2 1/2 cos cos , e v uu uvu uw txzxxz uug TT kK gCC (2) 2 2, e v vv vuv uw txzxt z v (3) 2 2, TT TT uw txz z (4) 2 2. CC CC uwD txz z (5) The initial conditions are 0,,( ,), 0, ,,, 0, ,,, 0, ,,, 0, ,,, i i i i i uxzuxz vxzvxz wxzuxz TxzTxz CxzCxz (6) 1 ,yv , u , w or ww Tq 2 T 0 Figure 1. Physical model and coordinate system. Copyright © 2011 SciRes. AM  1198 S. M. AL-HARBI and the boundary conditions are given by 1 1 1 2 ,,0,,0 0, ,,0sin 1, ,,0and ,,0, ,, 0, ,,sin 1, ,,and ,,, ww utx wtx vtx xst Ttx TCtx C utx vtx xst TtxT CtxC (7) here is the semi-vertical angle of the cone; is the kinematics viscosity; is the density; t and t are the dimensional and dimensionless times, respectively; 1 and 2 are the angular ve- locities of the cone and the fluid far away from the sur- face, respectively; 12 is the composite an- gular velocity; K and are the respective permeability and the inertia coefficient of the porous medium; tx sin is the porosity; g is the acceleration due to gravity; T is the temperature; C is the species concentration; is the volumetric co-efficient of thermal expansion; is the volumetric co-efficient of expansion for concentration; and D are thermal and mass diffusivity, respectively; Subscripts t, x and z denote partial derivatives with re- spect to the corresponding variables and the subscripts e, i, w and denote the conditions at the edge of the boundary layer, initial conditions, conditions at the wall and free stream conditions, respectively; , , 0 T0 C T and are constants. C Equations (1)-(5) are a system of partial differential equations with three independent variables x, z and t. It has been found that these partial differential equations can be reduced to a system of ordinary differential equa- tions, if we take the velocity at the edge of the boundary layer e and the angular velocity of the cone to vary inversely as a linear function of time. Consequently, ap- plying the following transformations: v 1 2 1/2 1/2 1 1 1/ 21/ 2 sin 1, sin 1, sin , ,,12 sin1, ,,sin 1, ,,sin1, e vx st st z tt utxzst f vtxzxst g wtxzst f (8) to Equations (1)-(5), we find that the continuity Equation (1) is identically satisfied, and Equations (2)-(5) reduce to, 2 22 1 1 2 121 2 1 22 0, fff fg Nsff ff (9) 1 2 1 12 0, fg gfsgg gg (10) 111 Pr2 0, 22 ffs (11) 111 20 22 Scff s , (12) where Re L Da is the first resistance parame- ter, is the second resistance parameter, 21 2 x Da /2 x 2 Re sinL L is the Reynolds number, 2 L DaKL is the Darcy number, 2 11 Re , Gr 2 22 Re Gr are the buoyancy parameters 32 10 cos ,GrTTLg 32 20 cosGrTTLg are the Grashof numbers, 11 is the angular ve- locity of the cone to the composite angular velocity, 21 N is the ratio of Grashof numbers, Pr is the Prandtl number and Sc D is the Schmidt number. s is the parameter characterizing the unsteady- ness in the free stream velocity 1 21sin e vxst 0 1st. The flow is accelerating if provided s and the flow decelerating if 0.s Further, 10 implies that the cone is stationary and the fluid is rotating, 11 represents the case where the cone is rotating in an ambient fluid, and for 10.5 , the cone and the fluid are rotating with equal angular velocity in the same direction. The ratio of Grashof numbers denoted by the parameter N measures the relative importance of thermal diffusion in inducing the buoyancy forces which drive the flow. N = 0 for no species diffusion, infinite for the thermal diffusion, positive for the case when the buoy- ancy forces due to temperature difference act in the same direction and negative when they act in the opposite di- rection. The boundary conditions Equation (7) can be expressed as 1 1 000,0 ,001 0,1 ,0. ffg fg , (13) Here is the similarity variable; f is the dimen- sionless stream function; and g are, the respectively dimensionless velocity along x- and y- directions; and Copyright © 2011 SciRes. AM  S. M. AL-HARBI 1199 are the dimensionless temperature and concentra- tion. The set of partial differential Equations (1)-(5) gov- erning the flow has to be solved subjected to initial con- ditions (6) and boundary conditions (7). The ordinary differential Equations (9)-(12) under the boundary condi- tions (13) are solved using the self-similar solution which implies that the solution at different times may be reduced to a single solutions i.e., the solution at the one value of time t is similar to the solution at any other value of time t. This similarity property permits a de- crease in the number of independent variables from three to one (in the present case) and yields treatment using ordinary differential equations instead of partial differen- tial equations. The quantities of physical interest are as follows: The surface skin friction co-efficient in x- and y- di- rections are, respectively, given by 2 1 0 1/2 2sin1 Re0 , fx z x Cuzxst f 2 1 0 1/2 2sin1 Re0 . fy z x Cvzx st g Thus 1/2 1/2 Re0 , Re0 , fx x fy x Cf Cg (14) where 1 2 Resin 1. xxst The Nusselt number and Sherwood number can be ex- pressed as: 1/ 2 1/2 Re 0 Re0 , x x Nu Sh (15) where 0w z NukT zTT and 0w z ShDCzCC 3. Results and Discussion The similarity Equations (9)-(12) are coupled nonlinear and exhibit no closed-form solution. Therefore, they must be solved numerically subject to the boundary con- ditions. The implicit finite-difference method with itera- tion similar to that discussed by Inouye and Tate [18] have proven to be successful for the solution of such equations and for this reason, it will be employed herein. The computations have been carried out with 0.01 (0 5), for various values of , Pr(7Pr 10) 11 ( 0.251.0), (0.22 2.57) Sc Sc (1 1),ss ( 0.51.0),NN 0.0,0.5,1.0, . The edge of the boundary layer 0.0,0.5,1.0 is taken between 4 and 6 depending on the values of parameters. In order to verify the correctness of our method, we have compared our results with those of Himasekher et al. [5] and Anilku- mar and Roy [10]. The results are found to be in excel- lent agreement and some of the comparisons are shown in Tables 1 and 2. Also the effects of and on the skin friction coefficients, Nusselt number and Sherwood number (1/ 2 Re xx C, 1/ 2 Re yx 1/2 Rex Nu C, , 1/2 Re Sh ) are presented in Tabl e 3. Figures 2-5 show the effect of the first resistance pa- rameter γ, the second resistance parameter Δ and the buoyancy parameter on the velocity profiles in the tangential direction f , on the temperature profiles and on the concentration profiles for accel- erating flows s0.5 , 1.0N , and P0.Sc 94 r 0.7 . The presence of a porous medium in the flow presents resistance to flow, thus, slowing the flow and increasing the pressure drop across it. Therefore, as the first and second resistances increases, Table 1. Comparison of the results (–f''(0), –g'(0), –θ'(0)) with those of Himasekher et al. [5] and Anilkumar and Roy [10]. Present results Pr (0)f (0)g (0) 1.0189 0.6155 0.4347 0.0 1.0256* 0.6158* 0.4299* 2.07736 0.84997 0.61173 1.0 2.2021* 0.8496* 0.6120* 8.52447 1.40365 1.01729 0.7 10 8.5041* 1.3990* 1.0097* 0.0 1.0189 0.6155 0.51858 1 1.0 2.00333 0.82459 0.7003 Anilkumar and Roy [10] 0.0 1.0199 0.6160 0.4305 1.0 2.1757 0.8499 0.6127 0.7 10 8.5029 1.4061 1.0175 0.0 1.0199 0.6160 0.51808 1 1.0 2.0627 0.8250 0.7005 *Values taken from Himasekher et al. [5]. Copyright © 2011 SciRes. AM  1200 S. M. AL-HARBI Table 2. Comparison of the results skin friction coefficients, Nusselt number and Sherwood number (1/2 Re xx C, , ) when N = 1.0, Pr = 0.7, Sc = 0.94 and s = 0.5 with those of (*) anilkumar and roy [10]. 1/2 Re fy x C 1/2 Rex Nu 1/ 2 Re fx x C 1/ 2 Re fy x C 1/2 Rex Nu 1/ 2 Rex Sh –1.27349 –1.33646 0.55691 0.66286 –0.5 –1.27215* –1.33537* 0.55580* 0.66305* 0.63047 –64157 0.82157 0.9514 0.0 0.63241* 0.63949* 0.81922* 0.95065* 1.3139 –0.2300 0.89215 1.02926 0.25 1.31339* –0.22765* 0.89011* 1.02812* 1.84895 0.19508 0.93841 1.08038 0.5 1.84798* 0.19806* 0.93700* 1.07977* 2.24483 0.62299 0.96586 1.11099 1 0.75 2.24659* 0.62679* 0.96563* 1.11132* 2.43469 –1.43508 0.91406 1.05979 –0.5 2.43934* –1.43105* 0.91210* 1.05951* 3.79418 –0.5989 1.0298 1.18687 0.0 3.79522* –0.59651* 1.02869* 1.18645* 4.31863 –0.13985 1.06614 1.22666 0.25 4.31854* –0.13691* 1.06539* 1.22639* 4.73919 0.33212 1.09142 1.25444 0.5 4.73958* 0.33552* 1.09111* 1.25444* 5.05751 0.80937 1.10715 1.27191 3 0.75 5.05951* 0.81201* 1.10712* 1.27223* 5.17896 –1.55388 1.06599 1.23185 –0.5 5.18154* –1.55129* 1.06503* 1.23177* 6.36087 –0.60918 1.14372 1.31644 0.0 6.36147* –0.60724* 1.14323* 1.31640* 6.82067 –0.10787 1.16935 1.34436 0.25 6.82071* –0.10547* 1.16887* 1.34416* 7.19184 0.40346 1.18759 1.36433 0.5 7.19231* 0.40602* 1.18730* 1.36415* 7.47488 0.91921 1.19912 1.3771 5 0.75 7.47647* 0.92102* 1.19926* 1.37740* Table 3. Skin friction coefficients, Nusselt number and Sherwood number (, , , 1/2 Re fx x C1/2 Re fy x C1/2 Rex Nu 1/2 Rex Sh ) for different values of the first resistance parameter γ and second resistance parameter Δ, when N = 1.0, λ = 1, Sc = 0.94 and s = 0.5, α = 0.5. Pr 1/ 2 Re fx x C1/ 2 Re fy x C 1/2 Rex Nu 1/2 Rex Sh 0.0 1.2545 –0.30646 0.93274 1.05144 0.5 1.38577 –0.40706 0.94519 1.06612 0.7 1.0 1.55139 –0.52446 0.96054 1.08416 0.0 1.04607 –0.32232 1.75335 1.02897 0.5 1.15386 –0.42986 1.7723 1.04142 3.0 1.0 1.29099 –0.55603 1.79581 1.0569 0.0 0.90501 –0.33192 2.61364 1.01487 0.5 1.00123 –0.44337 2.63338 1.02627 7.0 1.0 1.12502 –0.5743 2.65829 1.04062 Pr 1/ 2 Re fx x C1/ 2 Re fy x C 1/2 Rex Nu 1/2 Rex Sh 0.0 1.2545 –0.30646 0.93274 1.05144 0.5 1.27153 –0.28184 0.93426 1.05325 0.7 1.0 1.29145 –0.26046 0.93606 1.05538 0.0 1.04607 –0.32232 1.75335 1.02897 0.5 1.05068 –0.29681 1.75402 1.02933 3.0 1.0 1.05605 –0.27486 1.75481 1.02976 0.0 0.90501 –0.33192 2.61364 1.01487 0.5 0.90417 –0.30572 2.61336 1.01457 7.0 1.0 0.90359 –0.28324 2.61312 1.0143 the resistance due to the porous medium increases and the velocity components decrease further as shown in Figures 2 and 3. Also, the effects of , and on the temperature profiles and on the concentration profiles are shown in Figures 4 and 5. From these figures it is obvious that as the first and second resis- tances increases the temperature and concentration pro- files decrease. In Figures 6 and 7 the effects of the first resistance and the Prandtl number Pr on the temperature profiles and the effects of the first resistance and the Schmidt number Sc on the concentration profiles for 0.5s , 1.0N , 0.94Sc are presented. Also, the effects of , and Pr on the skin friction coefficients, Nusselt number and Sherwood number (1/2 Re xx C, 1/ 2 Re yx , , C 1/ Rex Nu 2 1/2 Re Sh ) are given in Table 3. Figures 6 Copyright © 2011 SciRes. AM 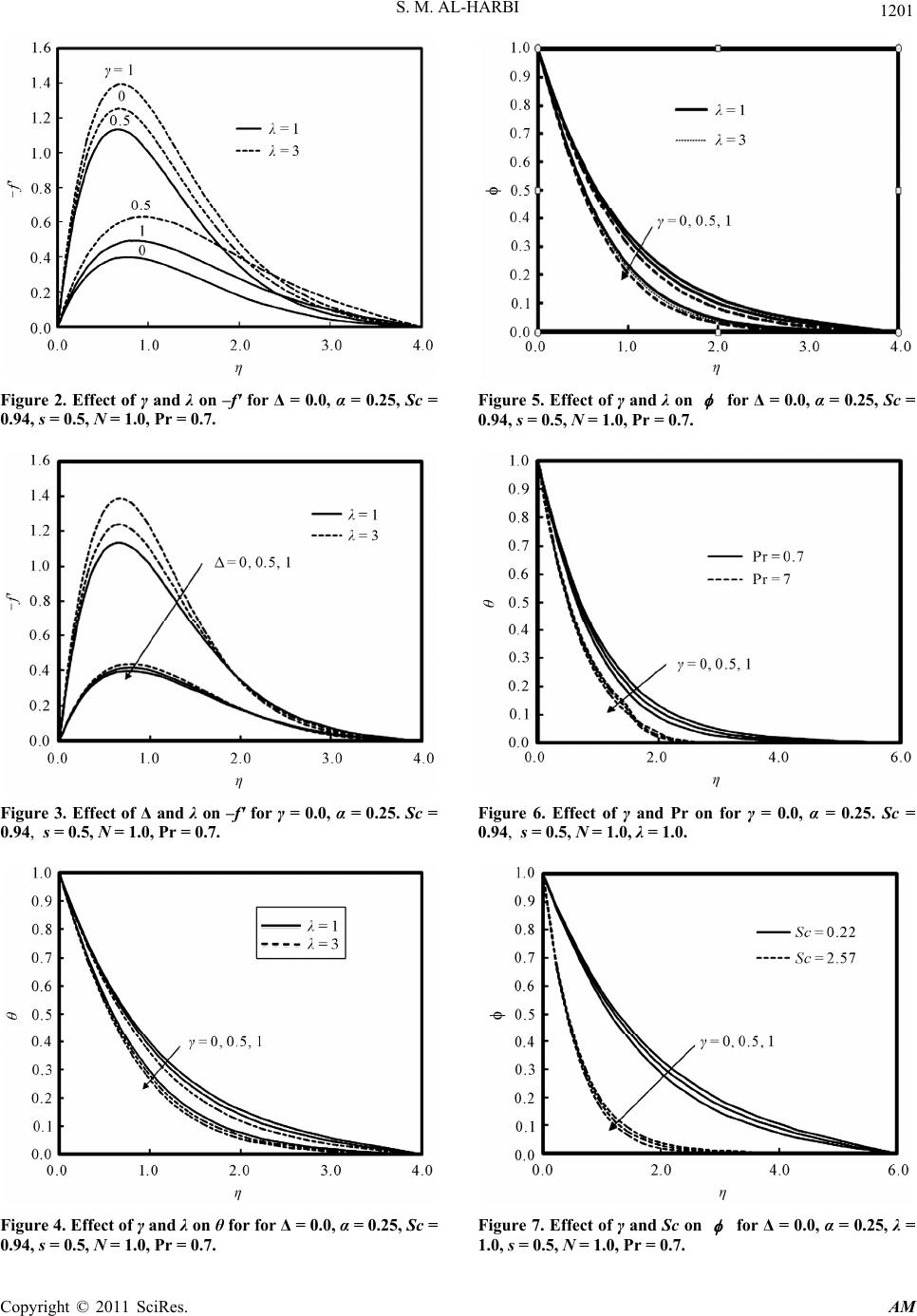 S. M. AL-HARBI 1201 Figure 2. Effect of γ and λ on –f' for Δ = 0.0, α = 0.25, Sc = 0.94, s = 0.5, N = 1.0, Pr = 0.7. Figure 3. Effect of Δ and λ on –f' for γ = 0.0, α = 0.25. Sc = 0.94, s = 0.5, N = 1.0, Pr = 0.7. Figure 4. Effect of γ and λ on θ for for Δ = 0.0, α = 0.25, Sc = 0.94, s = 0.5, N = 1.0, Pr = 0.7. Figure 5. Effect of γ and λ on for Δ = 0.0, α = 0.25, Sc = 0.94, s = 0.5, N = 1.0, Pr = 0.7. Figure 6. Effect of γ and Pr on for γ = 0.0, α = 0.25. Sc = 0.94, s = 0.5, N = 1.0, λ = 1.0. Figure 7. Effect of γ and Sc on for Δ = 0.0, α = 0.25, λ = 1.0, s = 0.5, N = 1.0, Pr = 0.7. Copyright © 2011 SciRes. AM  1202 S. M. AL-HARBI Figure 8. Effect of γ on Skin friction coefficients (1/ Re xx Cf , 1/ Re yx C ) for Δ = 0.0, λ = 1.0, α = 0.25, Sc = 0.94, N = 1.0, Pr = 0.7. Figure 9. Effect of γ on Nussellt and Sherood numbers (, ) for Δ = 0.0, λ = 1.0, α = 0.25, Sc = 0.94, N = 1.0, Pr = 0.7. 1/2 Rex Nu 1/2 Rex Sh Figure 10. Effect of Δ on Nussellt and Sherood numbers (, ) for γ = 0.0, λ = 1.0, α = 0.25, Sc = 0.94, N = 1.0, Pr = 0.7. 1/2 Rex Nu 1/2 Rex Sh Figure 11. Effect of Δ on Skin friction coefficients (1/ Re xx Cf , 1/ Re yx C ) for γ = 0.0, λ = 1.0, α = 0.25, Sc = 0.94, N = 1.0, Pr = 0.7. and 7 show that the increase in , Pr and Sc causes a reduction in thermal and concentration boundary layers, respectively. Hence in Table 3, 1/2 Re Nu increases with Pr and increases with Sc. 1/2 Rex Sh Figures 8-11 display the effects of the first order re- sistance parameter, the second order resistance parameter and the unsteady parameter S on the skin friction coef- ficients, Nusselt and Sherwood numbers (1/2 Re xx C, 1/ 2 Re yx C, , 1/2 Rex Nu 1/2 Re Sh ) for 1.0 , 0.25 , 0.94Sc and Pr0.7 . From these figures it can be seen that as the unsteady parameter S increases from –0.5 to 0.5, the skin friction coefficients (1/2 Re xx C, 1/2 Re yx C) decrease, where the Nusselt and Sherwood numbers (21/ Re Nu , 1/2 Re Sh ) increase. Further, the same behav- ior is noticed for both the first and second order resis- tances parameter. 4. References [1] J. P. Hartnett and E. C. Deland, “The Influence of Prandtl Number on the Heat Transfer from Rotating Non-Iso- thermal Disks and Cones,” ASME Journal of Heat Transfer, Vol. 83, 1961, pp. 95-96. [2] R. G. Hering and R. J. Grosh, “Laminar Free Convection from a Non-Isothermal Cone,” International Journal of Heat and Mass Transfer, Vol. 5, No. 11, 1962, pp. 1059- 1068. doi:10.1016/0017-9310(62)90059-5 [3] C. L. Tien and I. J. Tsuji, “A Theoretical Analysis of Laminar Forced Flow and Heat Transfer about a Rotating Cone,” ASME Journal of Heat Transfer, Vol. 87, 1965, pp. 184-190. [4] R. G. Hering and R. J. Grosh, “Laminar Free Convection from a Non-Isothermal Cone at Low Prandtl Number,” International Journal of Heat and Mass Transfer, Vol. 8, No. 10, 1965. pp. 1333-1337. doi:10.1016/0017-9310(65)90059-1 Copyright © 2011 SciRes. AM  S. M. AL-HARBI Copyright © 2011 SciRes. AM 1203 [5] K. Himasekhar, P. K. Sarma and K. Janardhan, “Laminar Mixed Convection from Vertical Rotating Cone,” Inter- national Communications in Heat and Mass Transfer, Vol. 16, No. 1, 1989, pp. 99-106. doi:10.1016/0735-1933(89)90045-6 [6] C. Y. Wang, “Boundary Layers on Rotating Cones, Discs and Axisymmetric Surfaces with a Concentrated Heat Source,” Acta Mechanica, Vol. 81, No. 3-4, 1990, pp. 245-251. doi:10.1007/BF01176992 [7] K. A. Yih, “Mixed Convection about a Cone in a Porous Medium: The Entire Regime,” International Communica- tions in Heat and Mass Transfer, Vol. 26, No. 7, 1999, pp. 1041-1050. doi:10.1016/S0735-1933(99)00093-7 [8] S. M. Al-Harbi, “Numerical Study of Natural Convection Heat Transfer with Variable Viscosity and Thermal Ra- diation from a Cone and Wedge in Porous Media,” Ap- plied Mathematics and Computation, Vol. 170, 2005, pp. 64-75. doi:10.1016/j.amc.2004.10.093 [9] H. S. Takhar, A. Chamkha and G. Nath, “Unsteady Mixed Convention Flow from a Rotating Vertical Cone with a Magnetic Field,” Heat and Mass Transfer, Vol. 39, No. 4, 2003, pp. 297-304. [10] D. Anilkumar and S. Roy, “Unsteady Mixed Convection Flow on a Rotating Cone in a Rotating Fluid,” Applied Mathematics and Computation, Vol. 155, No. 2, 2004, pp. 545-561. doi:10.1016/S0096-3003(03)00799-9 [11] I. Pop and D. B. Ingham, “Convective Heat Transfer: Mathematical and Computational Modeling of Viscous Fluids and Porous Media,” Pergamon, Oxford, 2001. [12] D. A. Nield and A. Bejan, “Convection in Porous Me- dia,” Springer-Verlag, New York, 2005. [13] I. A. Hassanien, F. S. Ibrahim and Gh. M. Omer, “Unsteady Free Convection Flow in the Stagnation-Point Region of a Rotating Sphere Embedded in a Porous Me- dium,” Mechanical Engineering, Vol. 7, 2004, pp. 89-98. [14] I. A. Hassanien, F. S. Ibrahim and Gh. M. Omer, “Unsteady Flow and Heat Transfer of a Viscous Fluid in the Stagnation Region of a Three-Dimensional Body Embedded in a Porous Medium,” Journal of Porous Me- dia, Vol. 9. No. 4, 2006, pp. 357-372. doi:10.1615/JPorMedia.v9.i4.60 [15] F. S. Ibrahim, A. M. Elaiw and A. A. Bakr, “Effect of Chemical Reaction and Radiation Absorption on the Un- steady MHD Free Convection Flow Past a Semi Infinite Vertical Permeable Moving Plate with Heat Source and Suction,” Communications in Nonlinear Science and Numerical Simulation, Vol. 13, No. 6, 2008, pp. 1056- 1066. doi:10.1016/j.cnsns.2006.09.007 [16] S. Roy, P. Datta and N. C. Mahanti, “Non-Similar Solu- tion of an Unsteady Mixed Convection Flow over a Ver- tical Cone with Suction or Injection,” International Jour- nal of Heat and Mass Transfer, Vol. 50, 2007, pp. 181- 187. doi:10.1016/j.ijheatmasstransfer.2006.06.024 [17] E. Osalusi, J. Side, R. Harris and P. Clark, “The Effect of Combined Viscous Dissipation and Joule Heating on Un- steady Mixed Convection MHD Flow on a Rotating Cone in a Rotating Fluid with Variable Properties in the Pres- ence of Hall and Ion-Slip Currents,” International Com- munications in Heat and Mass Transfer, Vol. 35, No. 4, 2008, pp. 413-429. doi:10.1016/j.icheatmasstransfer.2007.09.002 [18] K. Inouye and A. Tate, “Finite Difference Version Qua- silinearization Applied to Boundary Layer Equations,” AIAA Journal, Vol. 12, No. 4, 1974, pp. 558-560. doi:10.2514/3.49286
|