ABSTRACT

Let 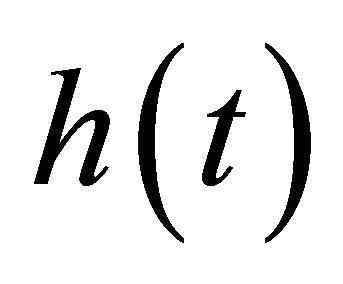be a smooth function, a standard Brownian motion and the first hitting time. In this paper, new formulations are derived to evaluate the probability density of the first hitting time. If denotes the density function of for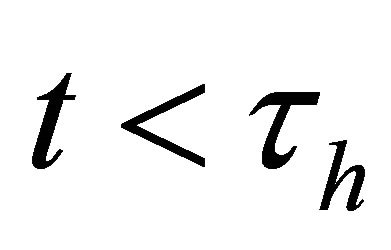, then and. Moreover, the hitting time density is. Applying some partial differential equation techniques, we derive a simple integral equation for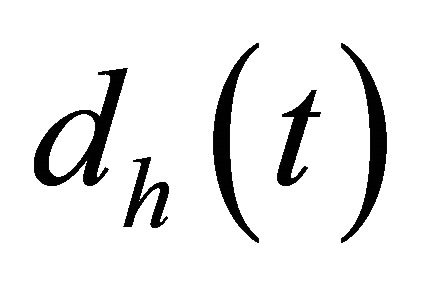. Two examples are demonstrated in this article.

1. Introduction

Since the publication of Black and Scholes’ [1], and Merton’s [2] papers in 1973, a stock price following a geometric Brownian motion becomes the standard model for the dynamics of a stock price. Therefore, the calculations for the first hitting time get important in the field of finance recently [3].

Let be a smooth function for, and a standard Brownian motion. The first hitting time is defined as. It is known that has a continuous density [4]. Sometime we call the function or the curve the barrier. For a constant barrier, the result has been wellknown for a long time. In this case, the density is

([5], Chapter 9). The distribution of the hitting time for non-constant barrier was considered by many authors; for example in [6-9]. In [6], Cuzick developed an asymptotic estimate for the first hitting density with a general barrier. In [7,8], the authors’ formulas contain an expected value of a Brownian function. The formulations in [7] are hard to see how the density for a general barrier is evaluated. Although the expected value in [8] can be evaluated by solving a partial differential equation, using a numerical method to compute the value is still not easy. In [9], the density function for parabolic barriers was expressed analytically in terms of Airy functions. In this article, we derive new exact formulations for the hitting density with a general barrier. Thus, partial differential equation (PDE) techniques may be applied to evaluate the density function of the first hitting time. Let be the probability density of;

i.e.. It will be shown that is the solution of an initialboundary value problem of a heat equation, and the hitting density is. Our derivation results a simple integral equation for the density function.

In Section 2, we show that the density function of the first hitting time can be evaluated though solving an initial-boundary value problem of the heat equation. Then, the density function will be the solution of a simple integral equation. In Section 3, a couple of examples are solved by PDE techniques to demonstrate the justification of the new method. The last section is the conclusion.

2. The Boundary Value Problem

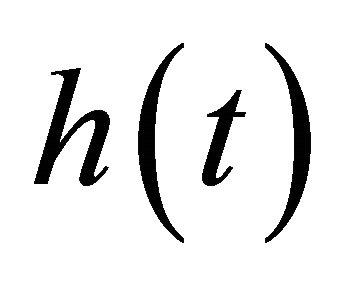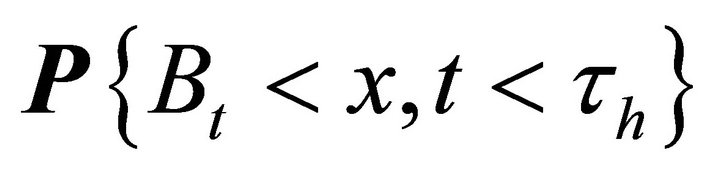Let B_t, , a standard Brownian motion, be a smooth function and the first hitting time. We consider first. Let denote the probability, and 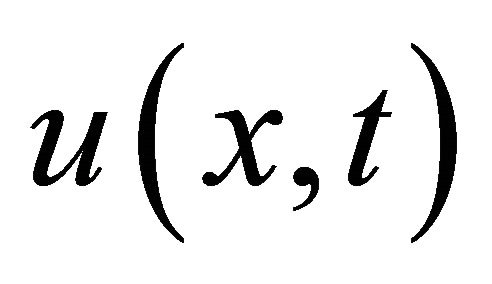denote the density function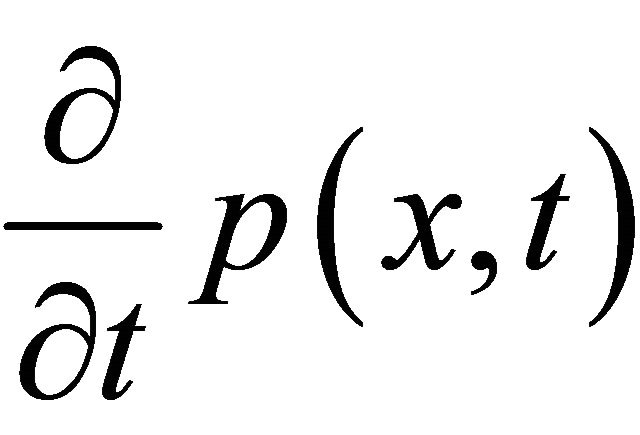. Surely, fulfills the heat equation, ([10], p. 352). Nevertheless, in this section, it will be proven with another way. To derive the formulations for, we consider the hitting problem at discrete times, where

. Let denote

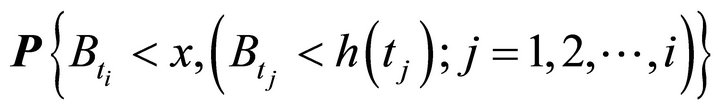and denote. Therefore,

(1)

where and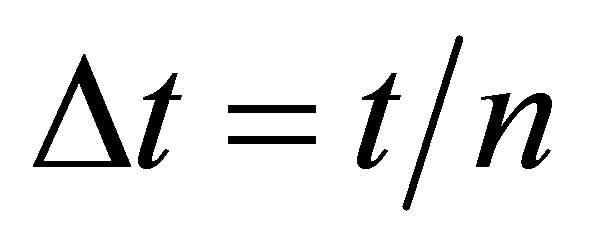. Taking the limit, we have

(2)

and

(3)

We will show that satisfies the heat equation. Integrating Equation (1), we have

(4)

for. The probability difference between two steps is

(5)

Using a substitution, , we have

where

Consequently,

(6)

Note that, if is continuous and bounded

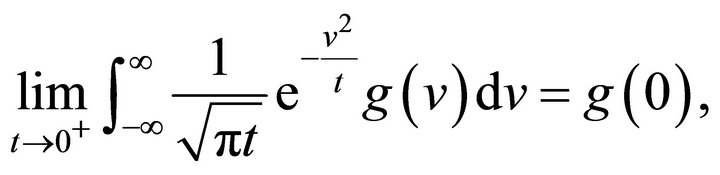
([11], p. 9) and, therefore, if

Let

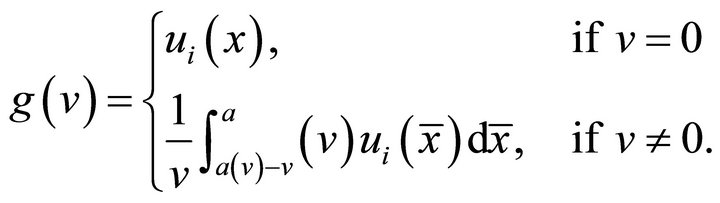
The function is continuous and bounded. Moreover, is differentiable, since

Thus, when 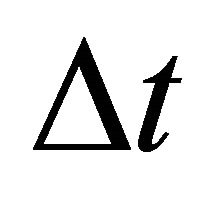approaches 0, the first term of the right-hand side of Equation (6) is. The second term is 0, because and, therefore, when is small. Letting approach 0, we have

(7)

Since, differentiating both sides of Equation (7) with respect to, we have the partial differential equation

(8)

The barrier is assumed to be differentiable, and, therefore, there exists an positive number not depending on such that. Consider the probability density near the boundary

(9)

where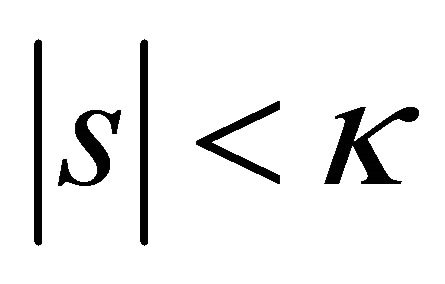. Note that

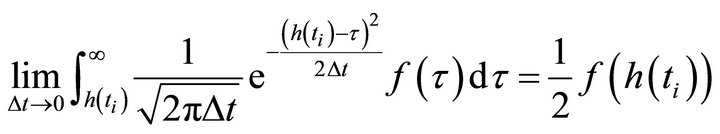
When,

Consequently,

We have the boundary condition

(10)

Therefore, we have a proposition as follows:

Proposition 1

The density function is subject to the initialboundary value problem:

(11a)

(11b)

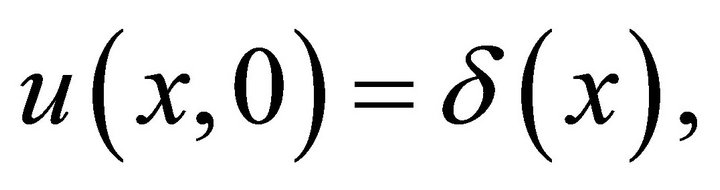(11c)

where is the Dirac delta function. The initialboundary value problem is mathematically well-post. The hitting probability,

(12)

Then, the hitting density

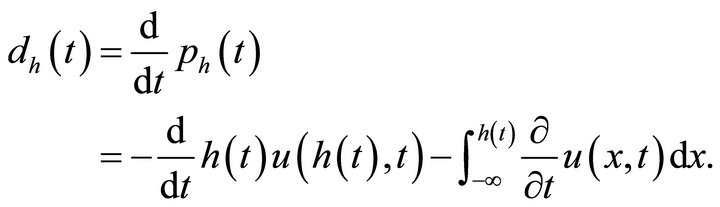(13)

Substituting Equations (8) and (10) into Equation (13), we have

Using integration by parts, we have

(14)

Similarly, if, the hitting density will be

. There is an integral equation for the boundary values of a heat equation ([12], p. 219).

(15)

where and

is the Heaviside step function. For problem (11), the integral equation becomes

or

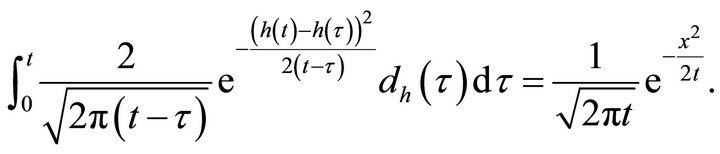(16)

Equation (16) can be solved by a numerical method easily.

3. Examples

Example 1: Linear boundaries.

Let with. The initial-boundary value problem (11) has a close-form solution. The solution, which is a Green’s function for the boundary, is

Thus, the hitting density is

consistent with that in [8].

Example 2: First-passage time probability in an interval.

Let 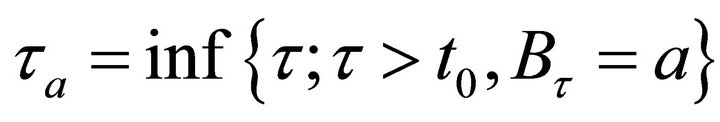and be the density function for. In this example, we evaluate the probability density of the first passage time.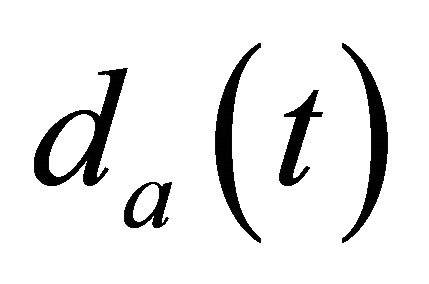

Let and

be the density of. Using and to denote the probability density

for and respectively, we have an initial-boundary value problem for both functions, and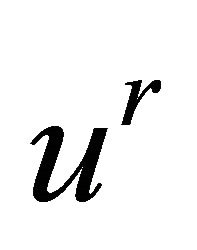. From the proposition, and fulfill the equations

and

The solutions are

and

The density function is

Thus

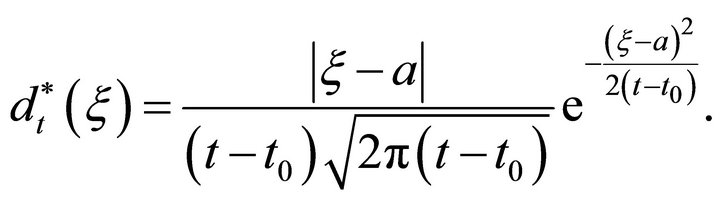
The density of has to be

(17)

where is the density function of; i.e.

The integral in Equation (17) can be calculated.

where and. Similarly,

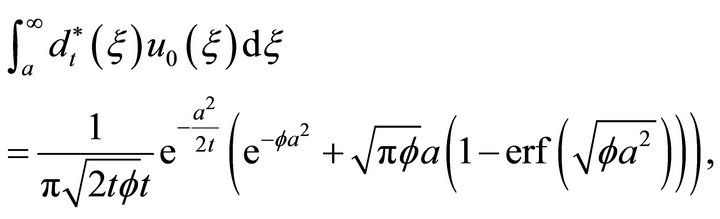
Therefore, the hitting rate

In the special case of,

The probability of that the Brownian motion process takes on the value 0 at least once in the interval is

This result is the same as in ([13], p. 191). In a simple case of,

This is the well-known result of the density of the first hitting time for a constant barrier.

4. Conclusions

The proposition proposed in Section 2 may offer a simple way to evaluate the density of the hitting time with a general barrier by solving an initial-boundary value problem of the heat equation. The density function locally satisfies the heat equation is well-known [10]. The main contribution of this paper is the derivation of the boundary condition (10). This result makes progress in the evaluation of hitting time density. Two examples with exact solutions are demonstrated in Section 3. Even though the examples may be solved by other method, the new formulations in this paper can be applied to evaluate the hitting time distribution with any smooth barrier numerically by using the integral Equation (16).

A similar result for two-dimensional problems may be expected. Let and be two standard Brownian motion, a smooth surface and

the first hitting time. If presents the probability density of for, the two-dimensional formulations may be as follows,

(18a)

(18b)

(18c)

As long as Equation (18) is established, the probability density of the first hitting time for two-dimensional Brownian motion may be evaluated by an analytical or numerical method.

REFERENCES

NOTES

^*Corresponding author.