Communications and Network
Vol. 5 No. 1 (2013) , Article ID: 28240 , 15 pages DOI:10.4236/cn.2013.51007
Fairness Assurance through TXOP Tuning in IEEE 802.11p Vehicle-to-Infrastructure Networks for Drive-Thru Internet Applications*
Department of Electronics and Communication Engineering, National Institute of Technology Calicut, Kozhikode, India
Email: harigovindan_pec10@nitc.ac.in, babu@nitc.ac.in, lilly@nitc.ac.in
Received December 21, 2012; revised January 22, 2013; accepted February 20, 2013
Keywords: Fairness; IEEE 802.11p; Residence Time; TXOP; Vehicle-to-Infrastructure Networks
ABSTRACT
This paper addresses an unfairness problem that exists among vehicles of distinct velocities in IEEE 802.11p based vehicle-to-infrastructure (V2I) networks used for drive-thru Internet applications. The standard IEEE 802.11p does not take into account, the residence time of vehicles within the coverage of each road side unit (RSU), for granting channel access. Due to this, a vehicle moving with higher velocity has less chance to communicate with the RSU, as compared to vehicles with lower velocity, due to its shorter residence time in the coverage area of RSU. Accordingly, the data transfer performance of a higher velocity vehicle gets degraded significantly, as compared to that of the vehicle with lower velocity, resulting in unfairness among them. In this paper, our aim is to resolve this unfairness problem by assigning the transmission opportunity (TXOP) limits to vehicles according to their mean velocities. Using an analytical model, we prove that tuning TXOP limit proportional to mean velocity can ensure fairness among vehicles belonging to distinct classes of mean velocities, in the sense of equal chance of communicating with RSU. Analytical results are validated using extensive simulations.
1. Introduction
Vehicular Ad-hoc Networks (VANETs) are highly mobile wireless ad hoc networks envisioned to provide support for road safety, traffic management, and comfort applications by enabling vehicle-to-vehicle (V2V) as well as vehicle-to-infrastructure (V2I) communications [1]. Each vehicle equipped with an On-Board Unit (OBU) can either transmit hop-by-hop to the destination using V2V communication or transmit to the RSU using V2I communication. The Dedicated Short Range Communications (DSRC) has been proposed as the emerging technology that supports vehicular communications. The Federal Communication Commission (FCC) in USA has approved 75 MHz of spectrum between 5850 and 5925 MHz for DSRC to enhance safety and productivity of the transportation systems. The Task Group known as IEEE 802.11p has been formed in 2004 for developing an amendment to the 802.11 standard to include vehicular environments, based on the ASTM E2213-02 specifications [2]. This amendment is currently known as IEEE 802.11p [3].The IEEE working group 1609 has been formed to specify additional layers of the protocol stack. The combination of IEEE 802.11p and the IEEE 1609 protocol suite is designated as WAVE (Wireless Access in Vehicular Environments).The overall WAVE architecture includes IEEE standards 1609.1 to 1609.4 (for resource management, security architecture, networking services, and multichannel operation, respectively), and IEEE 802.11p (for MAC and PHY) [1].
Besides the delivery of infotainment services, the role of typical V2I systems will include the provisioning of safety related, real-time, local, and situation-based services, such as speed limit information, safe distance warning, lane keeping support, intersection safety, traffic jam warning, and accident warning. All these services aim to prevent accidents by providing timely information directly to the car and/or to the driver. The goal of drivethru Internet [4,5] is to provide hot spots along the road—within a city, or on a highway. The main technical challenges for communication in V2I and V2V networks are the very high mobility of the nodes, highly dynamic topology, high variability in node density, and very short duration of communication.
The IEEE 802.11p uses an enhanced distributed channel access (EDCA) medium access control (MAC) sub-layer protocol based on distributed coordination function (DCF) [3]. DCF ensures equal channel access probabilities for the contending nodes; but cannot provide service differentiation if the nodes carry frames with different priority levels [6]. The EDCA mechanism [7] assigns four different priority classes for incoming packets at each node which are called Access Categories (AC). Each AC has its own channel access function when compared with the legacy DCF in which all packets exploit the same access function to acquire the channel. The EDCA mechanism defines the channel access parameters such as the Arbitration Inter frame Space (AIFS), the minimum Contention Window , the maximum CW
, the maximum CW 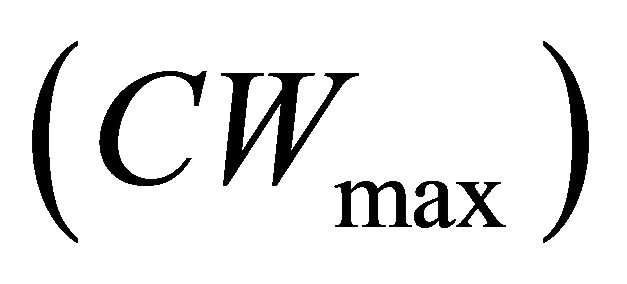 and the Transmission Opportunity (TXOP) per each AC in order to provide service differentiation [7]. During an EDCA TXOP, a node is allowed to transmit multiple Protocol Data Units (PDUs) from the same AC with a SIFS time gap between an ACK and the subsequent frame. Prior works [8-10] have proved that TXOP is an efficient techniques for providing service differentiation in 802.11 WLANs.
and the Transmission Opportunity (TXOP) per each AC in order to provide service differentiation [7]. During an EDCA TXOP, a node is allowed to transmit multiple Protocol Data Units (PDUs) from the same AC with a SIFS time gap between an ACK and the subsequent frame. Prior works [8-10] have proved that TXOP is an efficient techniques for providing service differentiation in 802.11 WLANs.
The problem of unfairness due to vehicles having different velocities has been analyzed in [11,12] for the V2I communication scenario shown in Figure 1, in which vehicles try to get connected to intermittent and serial RSUs along the highway. Vehicles having different velocities have different resident times in the coverage area of an RSU. However, DCF protocol does not take into consideration, the resident time of vehicles for granting channel access. Assuming a saturated network, if all the vehicles in the network use the same MAC parameters, DCF protocol provides equal transmission opportunity for all of them [6]. When vehicles have different velocities, they do not have similar chances of communication with RSU due to the different resident times and, therefore, a fairness problem exists. A fast moving vehicle has less chance to communicate with its RSU and consequently reduced data throughput performance as compared to a slow moving vehicle. This problem occurs for each area covered by an RSU. Therefore, the amount of data transferred at each area (useful for next areas) is not equal. In this paper, our aim is to resolve this unfairness problem by adjusting the TXOP of each vehicle according to its speed. In this way, the amount of successfully transmitted data of all vehicles is made equal regardless of their velocities, while residing in the coverage area of an RSU. Using Jain’s fairness index, we show how fairness in the sense of equal chance of communicating with RSU can be achieved by appropriate tuning of TXOP among vehicles of distinct mean velocity classes in the network. The impact of these choices on data throughput performance is also presented.
The rest of this paper is organized as follows. Section 2 presents a brief account of related work. In Section 3, we present the system model for V2I network and provide the expression for computing the data transferred. In Section 4, we discuss how bit-based fairness can be ensured by tuning TXOP limit according to mean velocity of vehicle. The analytical and simulation results are presented in Section 5. The paper is concluded in Section 6.
2. Related Work
Several attempts have been made to analyze and evaluate the performance of IEEE 802.11p standard for vehicular networks in terms of throughput and other related measures [11-23]. In [13,14], authors propose analytical models to evaluate the performance and the reliability of IEEE 802.11a-based V2V safety-related broadcast services in DSRC system on highway. Authors of [15] propose a simple but accurate analytical model to evaluate the throughput performance of DCF in the high speed V2I communications. They show that with node velocity increasing, throughput of DCF decreases monotonically due to mismatch between CW and mobility. In [16], the same authors used a 3D markov chain to evaluate the throughput of DCF in the drive-thru Internet scenario. In [17], authors propose an analytic model to evaluate the DSRC-based inter-vehicle communication. The impacts of the channel access parameters such as AIFS and CW are investigated. Analytical model for DSRC network that uses the IEEE 802.11 DCF MAC protocol is developed in [18]. In [19,20], authors derive analytical models to characterize the average and the distribution of the number of bytes downloaded by a vehicle by the end of its sojourn through an AP’s coverage range, in the presence of contention by other vehicles. Authors of [21] propose a new vehicular channel access scheme to compromise the trade-off between system throughput and throughput fairness in V2I networks. In [23], authors conduct a study on association control over the drive-thru Internet scenario for a V2I network. The overall aim is to improve the throughput and fairness for all the users.
The problem of unfairness due to vehicles having different velocities has been explained for a V2I scenario in [11,12] and for a V2V scenario in [22]. Authors of [11] present an analysis, in which the network that spans the coverage area of RSU is modeled as an M/G/1 queue. Using this model, they obtain an expression for the saturation throughput. They also approximate the number of packets transmitted by a node during its residence time by a Poisson random variable. Using these approximations and results from Bianchi’s analysis [6], they derive an approximation for the optimal 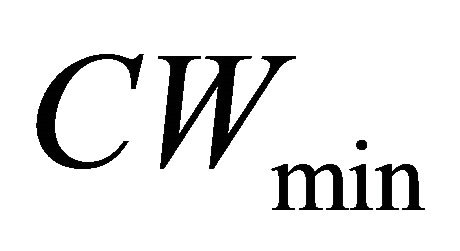 for fair access. In [12], optimal
for fair access. In [12], optimal  required for ensuring fairness, in the sense of equal chance of communicating with RSU, among competing vehicles of different mean velocities in the network, are evaluated. In [23], authors propose two dynamic CW based mechanisms to alleviate the performance degradation caused by vehicle mobility in V2V networks. But the paper does not describe the exact procedure for the selection of optimal CW value to achieve the objectives.
required for ensuring fairness, in the sense of equal chance of communicating with RSU, among competing vehicles of different mean velocities in the network, are evaluated. In [23], authors propose two dynamic CW based mechanisms to alleviate the performance degradation caused by vehicle mobility in V2V networks. But the paper does not describe the exact procedure for the selection of optimal CW value to achieve the objectives.
The effectiveness of TXOP based service differentiation has been extensively analyzed and evaluated in WLAN (e.g., [8-10]). In [8], the authors propose an analytical model to evaluate the impact of TXOP limits on the throughput of different access categories in WLANs. In [9], the authors incorporate the TXOP scheme into the infrastructure-based WLANs for throughput improvement. In [10], also authors propose TXOP adaptation to improve the performance of WLANs. In this paper, we study the impact of tuning TXOP on the data throughput performance of a V2I network in which vehicles are classified according to their mean velocities. The main objective is to resolve the unfairness among vehicles due to their distinct velocities.
3. Analytical Model for Data Transferred
The system model employed for the analysis includes models for highway and vehicle mobility, and is similar to that of [12]. Consider the V2I scenario, as shown in Figure 1, with vehicles connecting to intermittent and serial RSUs along the highway. Assume that each vehicle has always a frame ready for transmission (i.e.,saturation assumption). Also, we assume perfect channel conditions (i.e., no transmission errors), and neglect the effect of hidden and exposed terminals. Such assumptions are generally used for computing MAC layer throughput of wireless networks [6,12,15,16].
In application specific networks, like V2I, service providers will not pursue full coverage because of the high deployment and the maintenance costs, which in turn, results in non-coverage areas in the network. Even if they provide full coverage with contiguous areas covered by different RSUs and hand offs between them, some emergency information (e.g., status of traffic load, probable crashes occurred in the next road, etc.) must be communicated at each area. Since we are interested in the amount of information at each area (useful for next area) communicated to different vehicles, we focus on one coverage area (zone 1) and outside region (zone 0) only. Unlike [15] in which the system model has multiple zones within the coverage area of an RSU with distinct transmission rates determined by the distances of the nodes from the RSU, our system model has only one zone within the coverage area of an RSU.
We consider the highway to be multi lane, with N lanes, where lane  is used by vehicles with mean speed
is used by vehicles with mean speed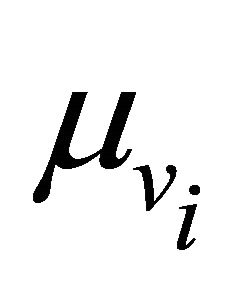 . Classifying the vehicles according to their mean speed, we have N classes of vehicles, a class
. Classifying the vehicles according to their mean speed, we have N classes of vehicles, a class  vehicle has a mean speed
vehicle has a mean speed . Let
. Let  be the no of vehicles belonging to class
be the no of vehicles belonging to class . The probability density function of
. The probability density function of , the random variable representing class
, the random variable representing class  vehicle velocity, is assumed to be uniform [14], [24] in the interval
vehicle velocity, is assumed to be uniform [14], [24] in the interval , with
, with 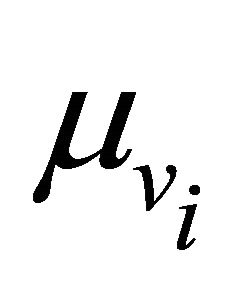 representing the mean and
representing the mean and  representing the standard deviation. Accordingly,
representing the standard deviation. Accordingly, ![]() is the maximum speed and
is the maximum speed and ![]() is the minimum speed. The pdf of
is the minimum speed. The pdf of 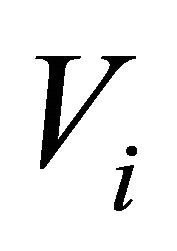 is given by
is given by
 (1)
(1)
The residence time of class  vehicle in the coverage area of RSU is a random variable defined as
vehicle in the coverage area of RSU is a random variable defined as 
 where
where  is the length of zone 1. The mean sojourn time of class
is the length of zone 1. The mean sojourn time of class  vehicle in the coverage area is calculated as follows [12]:
vehicle in the coverage area is calculated as follows [12]:
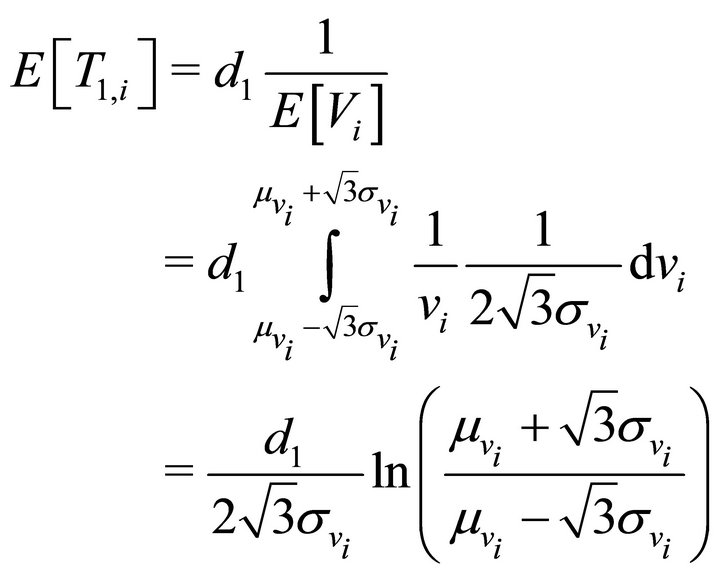 (2)
(2)
A class  vehicle entering zone 1 resides in the coverage area of the RSU for a mean time duration
vehicle entering zone 1 resides in the coverage area of the RSU for a mean time duration  before moving out. The mobility of vehicles can then be represented by the zone transitions using a Markov chain model as shown in Figure 2. To facilitate the use of discrete Markov chain model for the throughput analysis, the time that a class
before moving out. The mobility of vehicles can then be represented by the zone transitions using a Markov chain model as shown in Figure 2. To facilitate the use of discrete Markov chain model for the throughput analysis, the time that a class  node stays in each zone (zone 1 or zone 0), is assumed to be a geometrically distributed random variable with mean
node stays in each zone (zone 1 or zone 0), is assumed to be a geometrically distributed random variable with mean ,
, . Within a small duration,
. Within a small duration, ![]() , class
, class  vehicles in zone 1 either move to zone 0 with probability
vehicles in zone 1 either move to zone 0 with probability
 , or remain in zone 1 with probability
, or remain in zone 1 with probability . The limiting probability that a node is in zone 1 at any time is given by
. The limiting probability that a node is in zone 1 at any time is given by  , where
, where  is the length of zone 0. When a vehicle is within the communication range of RSU, packet transmissions are coordinated by the DCF protocol. The packet length is assumed to be fixed and same for all nodes. Let
is the length of zone 0. When a vehicle is within the communication range of RSU, packet transmissions are coordinated by the DCF protocol. The packet length is assumed to be fixed and same for all nodes. Let ![]() be the maximum value of back off stage (assumed to be equal for all the nodes),
be the maximum value of back off stage (assumed to be equal for all the nodes),  represent the CW in the
represent the CW in the  retry/retransmission for class
retry/retransmission for class  and
and ![]() denotes the maximum retry limit in DCF protocol. Further, it is assumed that, vehicles belonging to different mean velocity classes use the same AIFS which is equal to DIFS; but they can be configured to use different values for
denotes the maximum retry limit in DCF protocol. Further, it is assumed that, vehicles belonging to different mean velocity classes use the same AIFS which is equal to DIFS; but they can be configured to use different values for  and TXOP limit. With these assumptions the conditional frame transmission probability,
and TXOP limit. With these assumptions the conditional frame transmission probability, ![]() that the class
that the class  vehicle transmits a frame in a time slot, given that the vehicle is in zone 1, given by [12] (see the Equation (3) below).
vehicle transmits a frame in a time slot, given that the vehicle is in zone 1, given by [12] (see the Equation (3) below).
where
 .
.
Here  is the minimum CW of class
is the minimum CW of class  vehicle,
vehicle, 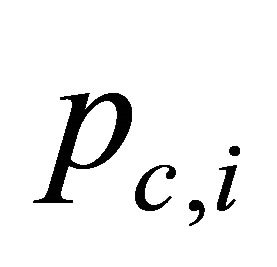 is the conditional collision probability for the class
is the conditional collision probability for the class  vehicle;
vehicle;  represents the mean collision duration; and
represents the mean collision duration; and  is the mean residence time for class
is the mean residence time for class  vehicle.
vehicle.
The conditional collision probability for the class  vehicle
vehicle  can be expressed in terms of the frame transmission probability
can be expressed in terms of the frame transmission probability ![]() as follows [6]:
as follows [6]:
 (4)
(4)
Let  be the probability that at least one vehicle transmits in a given slot time; clearly,
be the probability that at least one vehicle transmits in a given slot time; clearly,
 (5)
(5)
The conditional probability  that the transmission from a class
that the transmission from a class  vehicle is successful; is given by,
vehicle is successful; is given by,
 (6)
(6)
The average successful payload information transmitted for class  vehicles that are within the coverage area of RSU is computed as follows [10,12]:
vehicles that are within the coverage area of RSU is computed as follows [10,12]:

 (7)
(7)
where  is the average payload length (assumed to be equal for all nodes);
is the average payload length (assumed to be equal for all nodes);  is the probability that at least one vehicle transmits in a given slot time;
is the probability that at least one vehicle transmits in a given slot time; 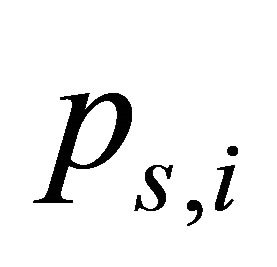 is the probability that a class
is the probability that a class  vehicle transmits and it is successful;
vehicle transmits and it is successful;  is the number of frames in one TXOP burst of class
is the number of frames in one TXOP burst of class  vehicle;
vehicle;  is the probability that a transmission that occur in a time slot is successful;
is the probability that a transmission that occur in a time slot is successful; ![]() is the duration of a empty time slot;
is the duration of a empty time slot;  is the mean sojourn time for class
is the mean sojourn time for class  within the coverage of RSU;
within the coverage of RSU;  and
and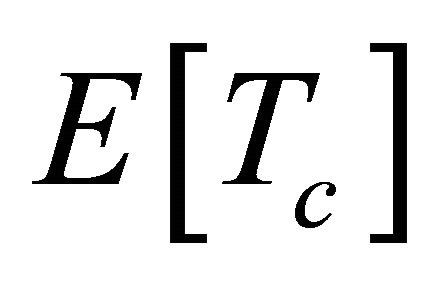 , respectively, represent the mean duration of successful and collision slots. Now assuming RTS/CTS scheme,
, respectively, represent the mean duration of successful and collision slots. Now assuming RTS/CTS scheme,  and
and  are computed as follows [10]:
are computed as follows [10]:
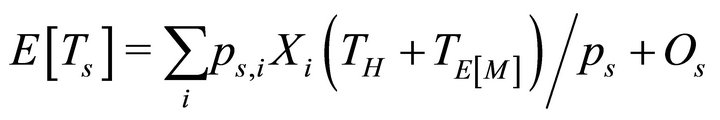
 (8)
(8)
Here where
where  and
and  represents the time required to transmit RTS and CTS packets respectively;
represents the time required to transmit RTS and CTS packets respectively;  and
and  denote the time to transmit the header (including MAC and Physical header) and an ACK, respectively. Further, SIFS and DIFS represents the short inter frame space and the distributed inter frame space respectively and are defined according to IEEE 802.11p standard. To compute the data transferred according to (7), first of all,
denote the time to transmit the header (including MAC and Physical header) and an ACK, respectively. Further, SIFS and DIFS represents the short inter frame space and the distributed inter frame space respectively and are defined according to IEEE 802.11p standard. To compute the data transferred according to (7), first of all, ![]() and
and  are determined using (3) and (4). Note that (3) and (4) form a system of non linear equations which can be solved using numerical techniques, to get
are determined using (3) and (4). Note that (3) and (4) form a system of non linear equations which can be solved using numerical techniques, to get ![]() and
and  [6,12]. With the knowledge of
[6,12]. With the knowledge of ![]() and
and ,
, 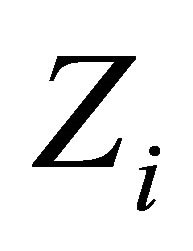 can be determined using (7) with the help of (4) to (6), (8) and (12). In V2I networks, the number of vehicles on the highway depends on parameters such as vehicle arrival rate, vehicle density, and vehicle speed. The total arrival rate
can be determined using (7) with the help of (4) to (6), (8) and (12). In V2I networks, the number of vehicles on the highway depends on parameters such as vehicle arrival rate, vehicle density, and vehicle speed. The total arrival rate  of class
of class  vehicles to the RSU can be determined as
vehicles to the RSU can be determined as
 (9)
(9)
where ![]() is the vehicle density on lane
is the vehicle density on lane  along the highway segment and
along the highway segment and  is the mean vehicle speed (m/sec). According to Greenshield’s model [25], the node density
is the mean vehicle speed (m/sec). According to Greenshield’s model [25], the node density ![]() linearly changes with the mean velocity
linearly changes with the mean velocity  as
as
 (10)
(10)
where  is the vehicle jam density at which traffic flow comes to a halt,
is the vehicle jam density at which traffic flow comes to a halt,  is the free moving velocity,
is the free moving velocity,
 (3)
(3)
i.e., the maximum speed with which vehicle can move, when the vehicle is driving alone on the road (usually taken as the speed limit of the road). The mean number of class  nodes,
nodes, 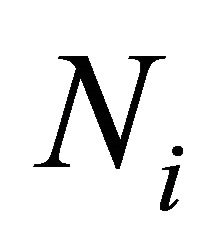 in the highway segment, is then determined using Little’s theorem as follows [12,15]:
in the highway segment, is then determined using Little’s theorem as follows [12,15]:
 (11)
(11)
The number of class  vehicles within the coverage area of RSU is given by
vehicles within the coverage area of RSU is given by
 (12)
(12)
4. Ensuring Fairness by TXOP Differentiation
Our objective is to ensure that all competing vehicles in the network achieve same amount of data transferred regardless of their velocities. Let  be the bits transferred per vehicle for class
be the bits transferred per vehicle for class  and let
and let 
be the total number of vehicles in the network. To ensure fairness, our aim is to achieve the following
 (13)
(13)
It may be noted that if all the vehicles in the network use the same data rate, (13) results in bit-based fairness.
4.1. Two Classes of Mean Velocities
In the discussion that follows, the subscripts ![]() and
and  correspond to classes of slow and fast vehicles, respectively. Let
correspond to classes of slow and fast vehicles, respectively. Let  denote the number of slow moving vehicles and
denote the number of slow moving vehicles and 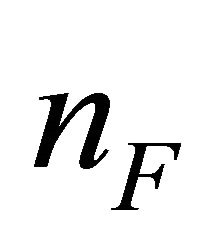 denote the number of fast moving vehicles. Also, let
denote the number of fast moving vehicles. Also, let  and
and , respectively, denote the mean velocities of the slow and fast moving vehicles and let
, respectively, denote the mean velocities of the slow and fast moving vehicles and let  and
and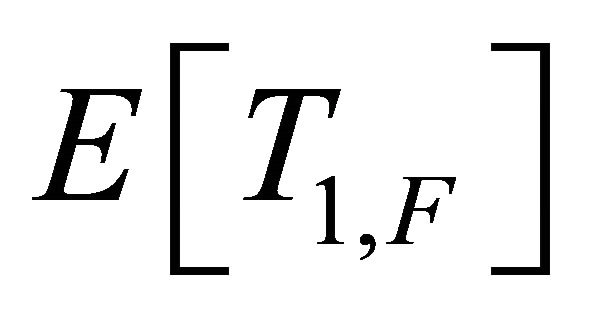 , respectively, be mean values of their residence times. Further, let
, respectively, be mean values of their residence times. Further, let 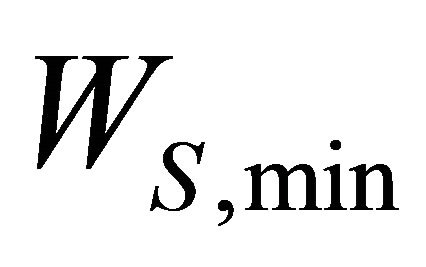 and
and  be the minimum CW corresponding to the two classes of velocities. Let the conditional frame transmission probabilities of slow and fast nodes be
be the minimum CW corresponding to the two classes of velocities. Let the conditional frame transmission probabilities of slow and fast nodes be  and
and , respectively; and the corresponding collision probabilities be
, respectively; and the corresponding collision probabilities be  and
and![]() . Using (3),
. Using (3),  and
and  can be respectively expressed as [6]:
can be respectively expressed as [6]:
 (14)
(14)
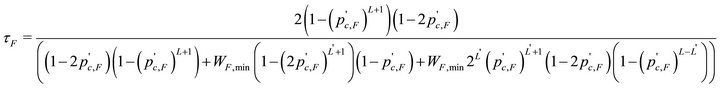 (15)
(15)
where

and
 .
.
Further, the collision probabilities  and
and ![]() are expressed as:
are expressed as:
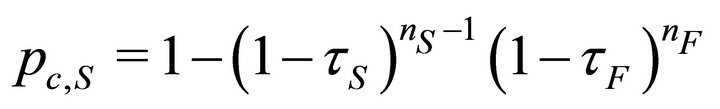
 (16)
(16)
Recall that  is the probability that there is at least one transmission in the given time slot, and let
is the probability that there is at least one transmission in the given time slot, and let ![]() and
and  be the corresponding probabilities for slow and fast nodes, respectively. These probabilites are calculated as follows:
be the corresponding probabilities for slow and fast nodes, respectively. These probabilites are calculated as follows:
 (17)
(17)
The successful transmission probabilities, as defined in (6), for the two classes are:

 (18)
(18)
The amount of bits transferred, for slow and fast moving vehicles are given by,

 (19)
(19)
Here  and
and 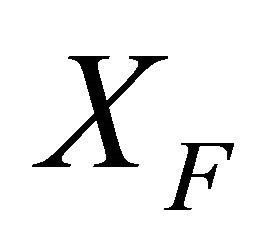 respectevely represents the number of frames in the TXOP burst of slow and fast vehicles respectively. We use the following Jain’s Fairness Index [26], in evaluating the fairness of channel access:
respectevely represents the number of frames in the TXOP burst of slow and fast vehicles respectively. We use the following Jain’s Fairness Index [26], in evaluating the fairness of channel access:
 (20)
(20)
where  is the total number of vehicles in the network, and
is the total number of vehicles in the network, and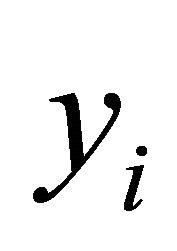 ’s are the individual vehicle share. It may be noted that
’s are the individual vehicle share. It may be noted that  and equality holds iff
and equality holds iff 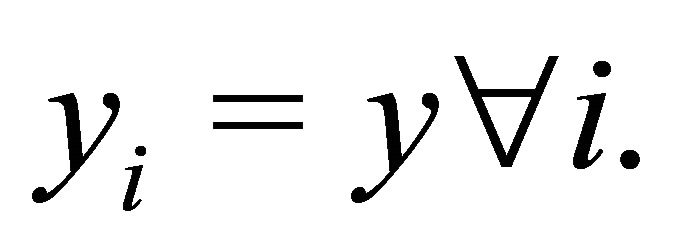 An approximate ratio of bits transferred per vehicle for slow and fast vehicles can be obtained using (16)-(19) as follows. Assume that
An approximate ratio of bits transferred per vehicle for slow and fast vehicles can be obtained using (16)-(19) as follows. Assume that  of all classes of vehicles are the same and differentiation is in terms of TXOP alone. From (18), we have
of all classes of vehicles are the same and differentiation is in terms of TXOP alone. From (18), we have
 .
.
Assume  and
and  so that
so that . Utilizing (19), we have the following approximation for the ratio of bits transferred for slow and fast vehicles. Then the ratio of data transferred per node for slow and fast vehicles is given by
. Utilizing (19), we have the following approximation for the ratio of bits transferred for slow and fast vehicles. Then the ratio of data transferred per node for slow and fast vehicles is given by
 (21)
(21)
Since  when
when , the optimal TXOP limit for the fast vehicle to achieve desired fairness objective can be obtained as follows:
, the optimal TXOP limit for the fast vehicle to achieve desired fairness objective can be obtained as follows:
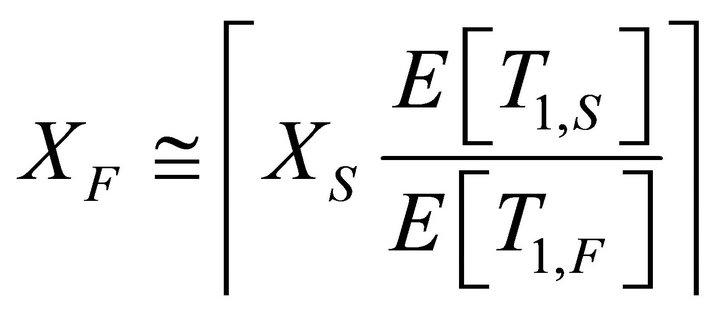 (22)
(22)
When optimal TXOP is chosen according to (21), the ratio of bits transferred per node for slow and fast vehicles become equal to unity, thus resulting in bit based fairness. Under default TXOP setting in which TXOP values are selected as equal, for all vehicles irrespective of their velocities, the above ratio is equal to the ratio of residence times of slow and fast vehicles.
4.2. Three Classes of Mean Velocities
In this section, we extend our analysis to a V2I network in which there are three classes of mean velocities: slow (S), medium (M) and fast (F). Let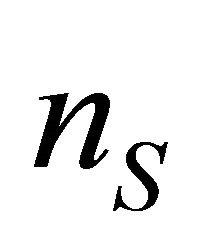 ,
,  ,
, 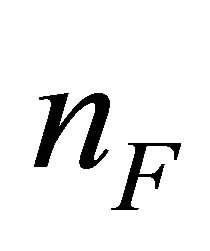 , respectively, denote the number of vehicles corresponding to the three categories.
, respectively, denote the number of vehicles corresponding to the three categories. ,
, ![]() and
and , respectively, be their mean velocities; and
, respectively, be their mean velocities; and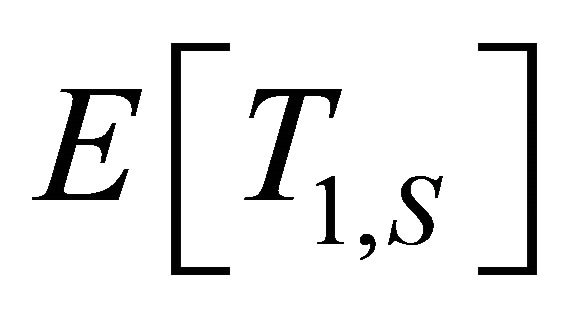 ,
, 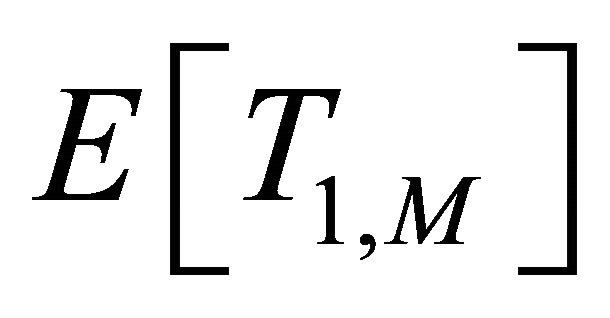
and , respectively, be their mean residence time. Clearly,
, respectively, be their mean residence time. Clearly, . Further, let
. Further, let ,
,  and
and 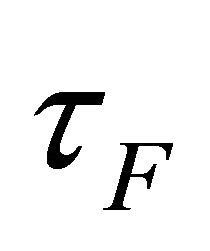 be the conditional frame transmission probabilities and let
be the conditional frame transmission probabilities and let ,
,  and
and ![]() be the frame collision probabilities of slow, medium and fast vehicles, respectively.
be the frame collision probabilities of slow, medium and fast vehicles, respectively.
To ensure fairness, the TXOP limits of medium and fast vehicles are to be increased to improve their opportunity for channel access. Keeping the TXOP of slowest vehicle constant at default value (unity), the optimal TXOP pair  required to achieve
required to achieve 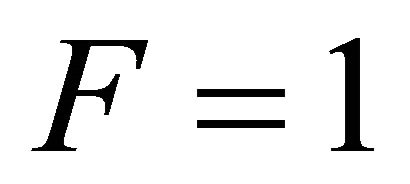 is determined. The fairness index F becomes equal to unity when
is determined. The fairness index F becomes equal to unity when , where
, where ![]()
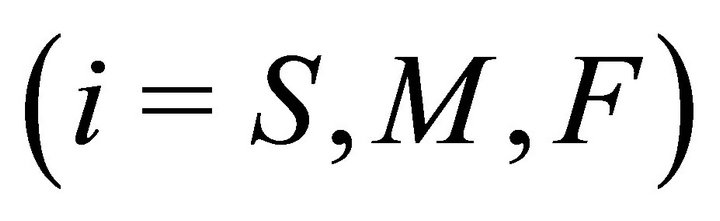 represent the bits transferred per node for slow, medium and fast nodes respectively. Assuming that
represent the bits transferred per node for slow, medium and fast nodes respectively. Assuming that  of all vehicles are same, expressions similar to (20) can be obtained as
of all vehicles are same, expressions similar to (20) can be obtained as

 (23)
(23)
Hence approximate expressions for optimal TXOP limits for medium and fast vehicles can be obtained as follows:

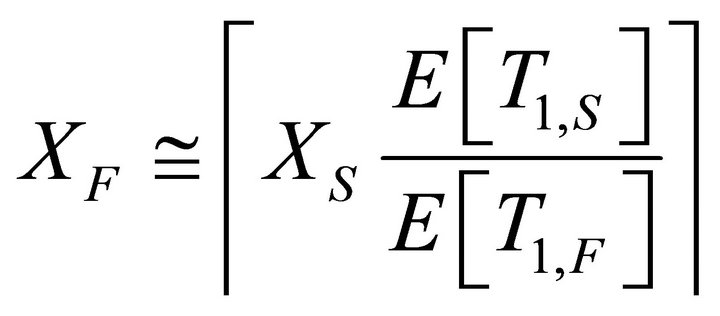 (24)
(24)
Note that  required to achieve bit based fairness in a network with three classes of mean velocities is same as that of two classes case. Also,
required to achieve bit based fairness in a network with three classes of mean velocities is same as that of two classes case. Also, 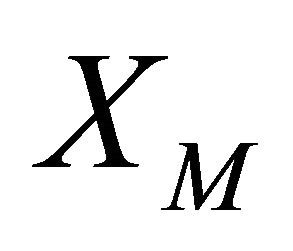 required to achieve bit based fairness in network with three classes of mean velocities is same as that required in a network two velocity classes, where the mean velocities are
required to achieve bit based fairness in network with three classes of mean velocities is same as that required in a network two velocity classes, where the mean velocities are ![]() and
and . Thus the optimal value of TXOP required to achieve bit based fairness in a network with two velocity classes, hold for network with three mean velocity classes as well. For a V2I network with N number of mean velocity classes, the results of (23) can be extended for all the higher velocity classes, provided we consider the slowest vehicle to be the reference node.
. Thus the optimal value of TXOP required to achieve bit based fairness in a network with two velocity classes, hold for network with three mean velocity classes as well. For a V2I network with N number of mean velocity classes, the results of (23) can be extended for all the higher velocity classes, provided we consider the slowest vehicle to be the reference node.
4.3. Joint Adaptation of TXOP and 
In this section, we consider joint adaptation of the  and TXOP among vehicles belonging to distinct mean velocity classes to ensure the desired fairness objective. We consider the case with two mean velocity classes. Let
and TXOP among vehicles belonging to distinct mean velocity classes to ensure the desired fairness objective. We consider the case with two mean velocity classes. Let 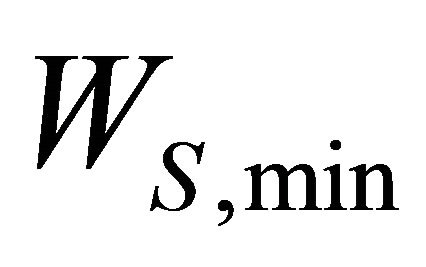 and
and  be the minimum CW of slow and fast vehicles. Assume
be the minimum CW of slow and fast vehicles. Assume ,
, 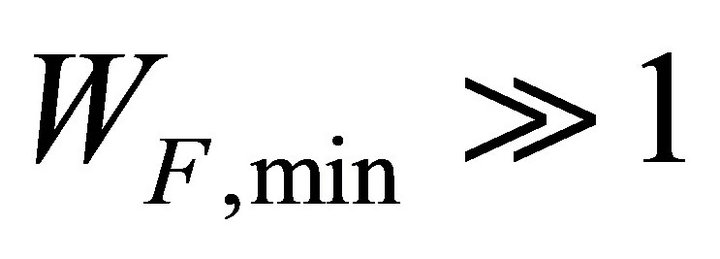 , so that
, so that . Also, let
. Also, let 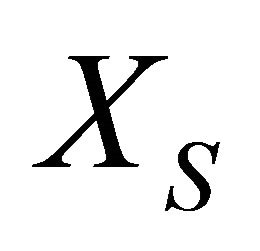 and
and  be the TXOP burst size corresponding to these two velocity classes. An approximate expression of ratio of data transferred per node for slow and fast vehicles can be obtained by using (16)-(19) as follows:
be the TXOP burst size corresponding to these two velocity classes. An approximate expression of ratio of data transferred per node for slow and fast vehicles can be obtained by using (16)-(19) as follows:
 (25)
(25)
Then using (14), (15) and assuming the retry limit to be infinite, the following approximation is valid [12]:
 .
.
Then ratio of the bits transferred,
 is given by
is given by
 (26)
(26)
The ratio of the bits transferred per node is given by
 (27)
(27)
To provide fairness in terms of data transferred, we have to ensure that 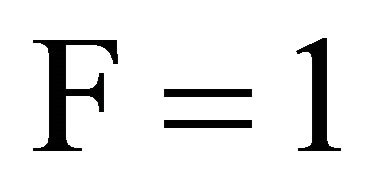 which makes
which makes . To ensure this, we consider combined tuning of
. To ensure this, we consider combined tuning of  and
and  of fast vehicles according to the following relation:
of fast vehicles according to the following relation:
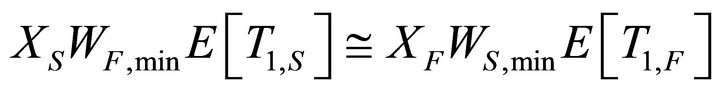
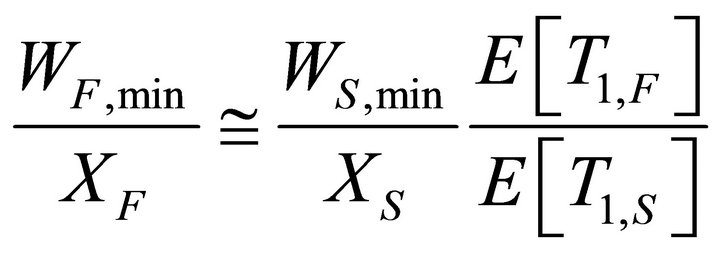 (28)
(28)
We can select default values for  and
and ; and compute
; and compute 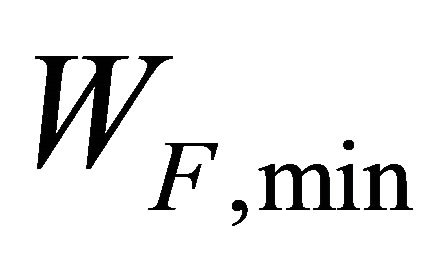 and
and , so as to satisfy (27), thus we ensure the ratio of bits transferred for slow and fast vehicles equal to unity.
, so as to satisfy (27), thus we ensure the ratio of bits transferred for slow and fast vehicles equal to unity.
5. Analytical and Simulation Results
In this section, we present the analytical and simulation results. The analytical results correspond to the mathematical model presented in the previous section and are obtained using MATLAB. To validate the analytical results, we simulate a IEEE 802.11p based V2I network using an event driven custom simulation program,written in C++ programming language. It may be noted that the MAC layer of IEEE 802.11p is based on EDCA and physical layer is based on IEEE 802.11a. A drive-thru Internet scenario as shown in the Figure 1 is simulated, in which RSU is deployed along the road and vehicles passing through compete for communication. The whole road length is divided into two segments with one zone in the coverage area of RSU and other zone representing the region outside the coverage of RSU (we set  and
and ). We simulate the road segment as composed of as many lanes as the number of classes of vehicles; e.g., for the case of three classes, a three lane road segment is simulated. Vehicle of class
). We simulate the road segment as composed of as many lanes as the number of classes of vehicles; e.g., for the case of three classes, a three lane road segment is simulated. Vehicle of class  arrive according to a Poission process with rate
arrive according to a Poission process with rate  veh/sec. Lane
veh/sec. Lane  is used by vehicles belonging to class
is used by vehicles belonging to class  of velocity
of velocity![]() . The probability distribution for
. The probability distribution for ![]() is assumed to be uniform between the interval
is assumed to be uniform between the interval  with
with  representing the mean vehicle speed and
representing the mean vehicle speed and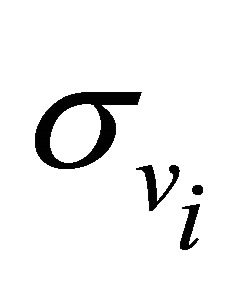 , the standard deviation. We consider traffic jam density
, the standard deviation. We consider traffic jam density  veh/km/lane and the free flow speed is selected as
veh/km/lane and the free flow speed is selected as  km/hr [25]. The system parameters used for simulation as well as for finding the numerical results from analysis are given in Table 1. All reported simulation results are averages over multiple 100 sec simulations.
km/hr [25]. The system parameters used for simulation as well as for finding the numerical results from analysis are given in Table 1. All reported simulation results are averages over multiple 100 sec simulations.
The number of vehicles corresponding to different classes of mean velocities, within the coverage area of RSU, are obtained using (12) with : 80 veh/km/lane. Table 2 lists the number of slow and fast vehicles in a network with two classes of mean velocities and Table 3 lists the number of vehicles in a network with three classes of mean velocities for different choices of mean velocities. These results are later used to investigate the data throughput performance of V2I networks. Table 4 shows the TXOP values required to ensure fairness, for a network in which the vehicles belong to two classes of mean velocities, and Table 5 shows corresponding results for a network that consist of vehicles categorized in to three classes of mean velocities.
: 80 veh/km/lane. Table 2 lists the number of slow and fast vehicles in a network with two classes of mean velocities and Table 3 lists the number of vehicles in a network with three classes of mean velocities for different choices of mean velocities. These results are later used to investigate the data throughput performance of V2I networks. Table 4 shows the TXOP values required to ensure fairness, for a network in which the vehicles belong to two classes of mean velocities, and Table 5 shows corresponding results for a network that consist of vehicles categorized in to three classes of mean velocities.
To find the data transferred, the MAC parameters for slow and fast vehicles are kept the same: ,
,  ,
,  ,
, . The default TXOP values are selected to be equal to unity. Further, we select
. The default TXOP values are selected to be equal to unity. Further, we select 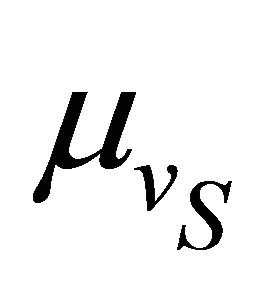 = 30/40/60 km/hr,
= 30/40/60 km/hr, 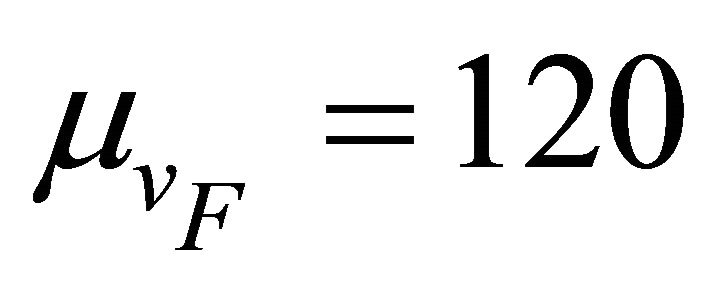 km/hr,
km/hr,  veh/km/lane,
veh/km/lane, 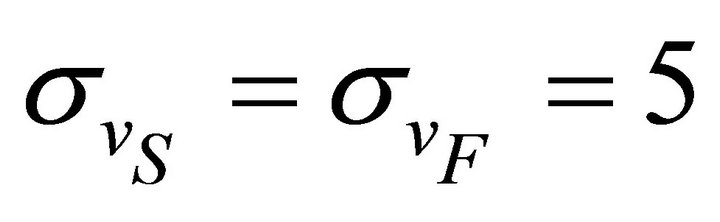 km/hr and
km/hr and  km/hr. The number of vehicles corresponding to these specifications are listed in Table 2. We evaluate the fairness index, according to (20) for default TXOP as well as optimal TXOP values, and the results are shown in Table 6. It can be observed that with optimal TXOP
km/hr. The number of vehicles corresponding to these specifications are listed in Table 2. We evaluate the fairness index, according to (20) for default TXOP as well as optimal TXOP values, and the results are shown in Table 6. It can be observed that with optimal TXOP

Table 1. System parameters.

Table 2. Network size: two classes of mean velocities.

Table 3. Network size: three classes of mean velocities.
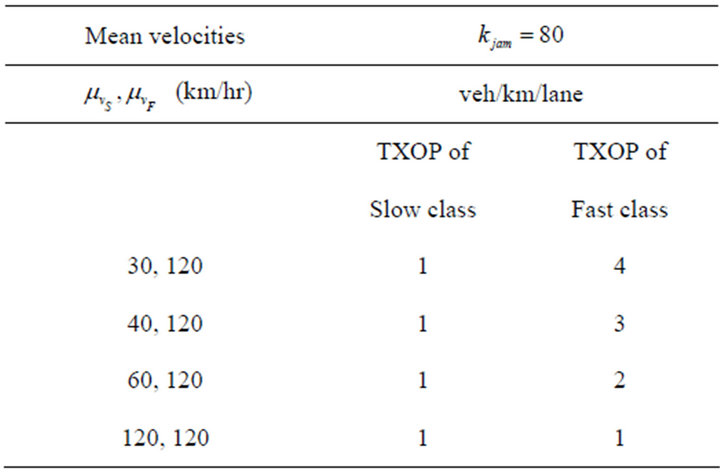
Table 4. TXOP to ensure fairness (two classes).

Table 5. TXOP to ensure fairness (three classes).
settings, the fairness index can be made equal to unity. We find the amount of data transferred for slow and fast vehicles by analysis using (19) as well as by simulation. The results are shown in Table 7. We find that the data transferred for fast vehicles is very low compared to slow vehicles with default TXOP settings. The low data transfer for fast vehicle is caused by the DCF protocol which does not consider residence time of a vehicle for granting channel access. Further, we observe that for default MAC settings, the ratio of data transferred per node for slow and fast vehicles is equal to the ratio of their mean residence times, thus validating our analytical result of (21). When TXOP values are selected according to (21), the amount of data transferred by slow as well as fast vehicles are observed to be equal. However, we observe a slight reduction in the total amount of data transferred (in Table 7) for the optimal case compared to the default case. This is in accordance with the established result on trade off between fairness and efficiency.
In Figure 3 aggregate data transferred in a network with two classes of mean velocities, plotted against the mean velocity of slow vehicle , keeping the mean velocity of fast vehicle as fixed:
, keeping the mean velocity of fast vehicle as fixed:  km/hr. It is observed that the aggregate data transferred decreases as
km/hr. It is observed that the aggregate data transferred decreases as  increases. This happens because, as
increases. This happens because, as  increases the mean residence time reduces, resulting in reduced channel access for slow vehicle as well. Figure 4 shows the ratio of data transferred per node for fast and slow vehicle
increases the mean residence time reduces, resulting in reduced channel access for slow vehicle as well. Figure 4 shows the ratio of data transferred per node for fast and slow vehicle , plotted against the mean velocity of slow vehicle (
, plotted against the mean velocity of slow vehicle ( km/hr).
km/hr). 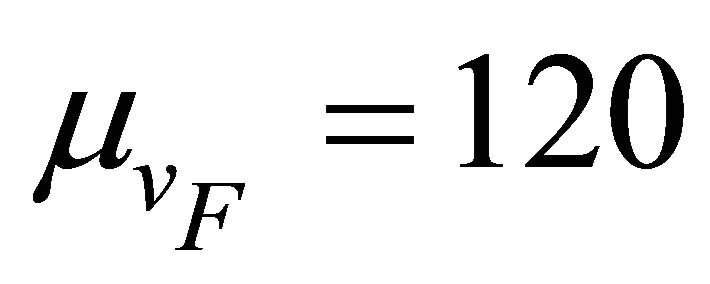 km/hr and
km/hr and 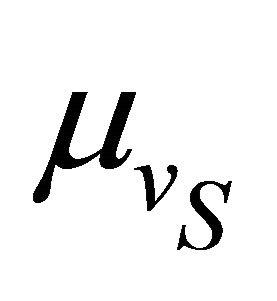 is varied from 30 km/hr to 120 km/hr. In default case, the ratio
is varied from 30 km/hr to 120 km/hr. In default case, the ratio 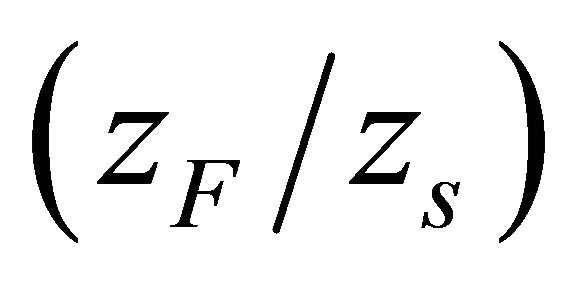 is equal to unity when
is equal to unity when  is 120 km/hr, and decreases as
is 120 km/hr, and decreases as 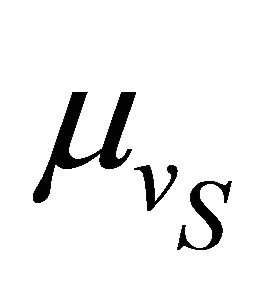 decreases. This happens because, as
decreases. This happens because, as  decreases, its residence time within RSU’s coverage increases and hence
decreases, its residence time within RSU’s coverage increases and hence 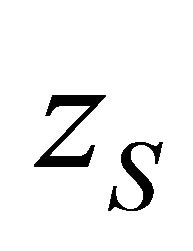 increases. When the optimal TXOP settings are used, both the slow and fast vehicles get the same chances of communication with the RSU, and hence the ratio of data transferred is almost equal to unity irrespective of
increases. When the optimal TXOP settings are used, both the slow and fast vehicles get the same chances of communication with the RSU, and hence the ratio of data transferred is almost equal to unity irrespective of .
.

Table 6. Fairness Index with default TXOP and optimal TXOP for two classes ( = 80 veh/km/lane,
= 80 veh/km/lane,  =
=  = 5 km/hr).
= 5 km/hr).
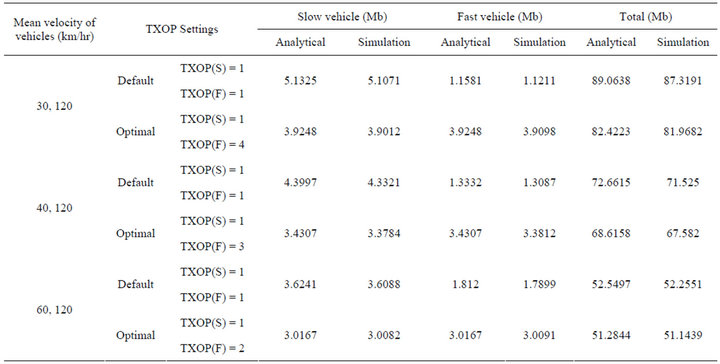
Table 7. Data transferred (individual and aggregate) with default and optimal TXOP values for two classes ( = 80 veh/km/lane,
= 80 veh/km/lane,  =
=  = 5 km/hr).
= 5 km/hr).
5.1. Three Classes of Vehicles
To find the data transferred for a network with three classes of mean velocities, we set  veh/ km/lane,
veh/ km/lane,  km/hr and
km/hr and  km/hr. The number of slow/medium/fast vehicles corresponding to these traffic parameters are listed in
km/hr. The number of slow/medium/fast vehicles corresponding to these traffic parameters are listed in
Table 3. The optimal TXOP values according to (23) are given in Table 5. The fairness index calculated with default and optimal TXOP limits are shown in Table 8. With optimal TXOP, it is observed that  can be achieved. With these optimal TXOP values, we evaluate the aggregate data transferred by slow, medium and fast
can be achieved. With these optimal TXOP values, we evaluate the aggregate data transferred by slow, medium and fast

Table 8. Fairness Index with default and optimal TXOP values for three classes ( = 80 veh/km/lane,
= 80 veh/km/lane,  =
=  =
=  = 5 km/hr).
= 5 km/hr).

Figure 1. Vehicle to infrastructure scenario.

Figure 2. Markov chain model for zone transitions.
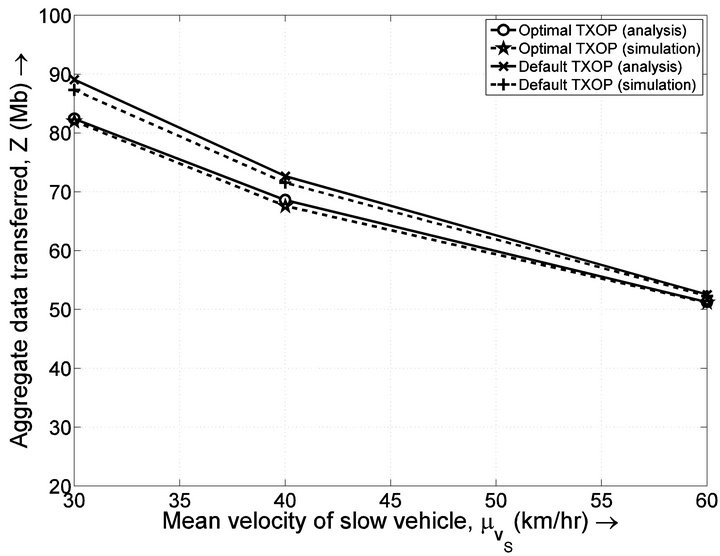
Figure 3. Aggregate data transferred vs mean velocity of slow station( = 120 km/hr and
= 120 km/hr and  = 80,
= 80,  =
=  = 5 km/hr).
= 5 km/hr).

Figure 4. Ratio of data transferred per node vs velocity of slow vehicle with default scheme and TXOP tuning ( = 120 km/hr,
= 120 km/hr,  =
=  = 5 km/hr).
= 5 km/hr).
vehicles. We repeat this calculation for the default TXOP values as well. Both the analytical and simulation results are shown in Table 9. For the default selection of TXOP limits, we find that the amount of data transferred by fast and medium velocity vehicles are very less compared to that of the slow vehicle. With optimal TXOP values, all the vehicles in the network transfer almost equal amount of data, irrespective of their mean velocities; thus ensuring fairness.
5.2. Impact of Standard Deviation of Vehicle Speed
In this section, we describe the impact of standard deviation of vehicle speed on the data throughput performance of V2I network, considering vehicles belonging to two classes of mean velocities. Figure 5 shows the impact of standard deviation of vehicle speed corresponding to slow moving vehicle , on the optimal TXOP limit
, on the optimal TXOP limit  of the fast vehicle. We keep the mean velocity of the slow and fast vehicles as follows:
of the fast vehicle. We keep the mean velocity of the slow and fast vehicles as follows:  km/hr and
km/hr and  km/hr. Further, the standard deviation of the fast vehicle is kept equal to
km/hr. Further, the standard deviation of the fast vehicle is kept equal to  km/hr. For lower values of
km/hr. For lower values of ,
,  remains invariant with respect to
remains invariant with respect to . However, when
. However, when  becomes greater than 10 km/hr,
becomes greater than 10 km/hr,  increases significantly for the case with
increases significantly for the case with  km/hr. This is due to the increase in mean residence time
km/hr. This is due to the increase in mean residence time  of slow vehicle arising out of increase in
of slow vehicle arising out of increase in 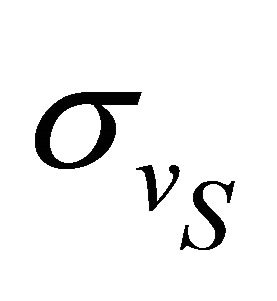 as predicted by (2).
as predicted by (2).
In Figure 6, we plot the fairness index against , for the default and optimal TXOP values. We keep the mean velocities of both class of vehicles to be fixed (i.e.,
, for the default and optimal TXOP values. We keep the mean velocities of both class of vehicles to be fixed (i.e.,  km/hr,
km/hr, 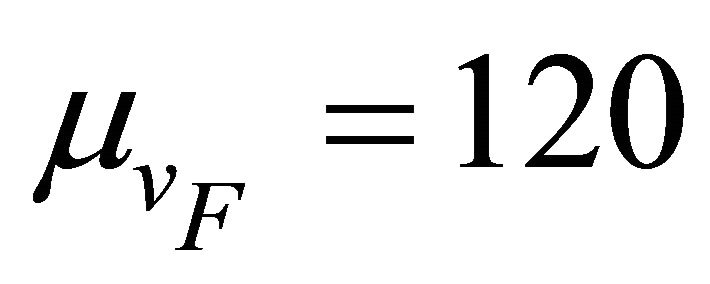 km/hr) and fix the standard deviation of fast vehicle as
km/hr) and fix the standard deviation of fast vehicle as  km/hr. We find the amount of data transferred for each class of vehicle and evaluate the fairness index. For the default setting, we select
km/hr. We find the amount of data transferred for each class of vehicle and evaluate the fairness index. For the default setting, we select . It is observed that, for the default TXOP settings, the fairness index degrades significantly as
. It is observed that, for the default TXOP settings, the fairness index degrades significantly as  increases. This happens because with increase of
increases. This happens because with increase of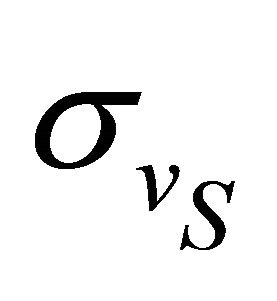 , the mean residence time of slow velocity vehicle
, the mean residence time of slow velocity vehicle  increases in accordance (2), assuming that mean velocity
increases in accordance (2), assuming that mean velocity  is constant. Accordingly, the amount of data transferred by a slow vehicle gets improved; which results in the degradation of fairness index. It is observed that with optimal TXOP values, the fairness index is insensitive to
is constant. Accordingly, the amount of data transferred by a slow vehicle gets improved; which results in the degradation of fairness index. It is observed that with optimal TXOP values, the fairness index is insensitive to  variations and is always equal to unity.
variations and is always equal to unity.
Figure 7 shows the impact of standard deviation of vehicle speed corresponding to slow moving vehicle on the ratio of data transferred per node for fast and slow vehicle . The behavior of this plots can be explained in the same way as explained for the fairness plots of Figure 6.
. The behavior of this plots can be explained in the same way as explained for the fairness plots of Figure 6.
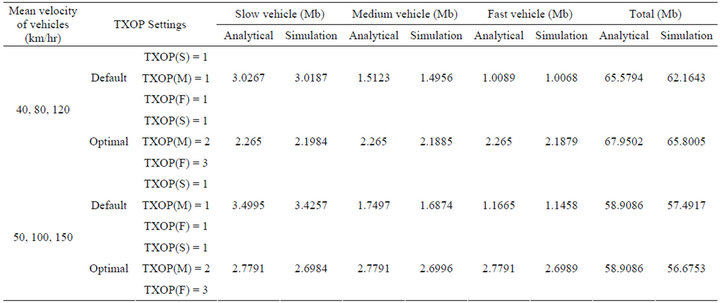
Table 9. Data transferred (individual and aggregate) with default and optimal TXOP values for three classes ( = 80 veh/km/lane,
= 80 veh/km/lane,  =
=  =
=  = 5 km/hr).
= 5 km/hr).

Figure 5. TXOP of fast vehicle vs standard deviation of slow vehicle speed ( = 5 km/hr).
= 5 km/hr).
5.3. Combined Tuning of TXOP and 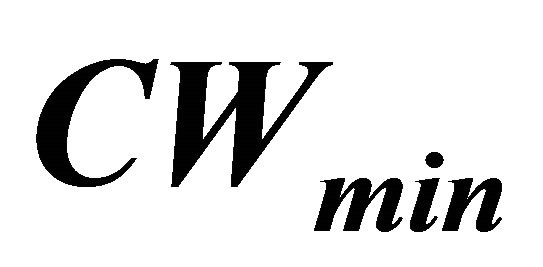
Next we consider combined tuning of TXOP and . Table 10 lists the values of TXOP and
. Table 10 lists the values of TXOP and 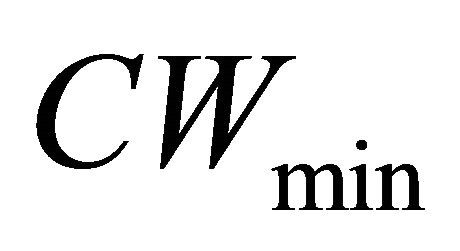 required for satisfying the desired fairness objective. With these values, we compute the amount of data transfered. Also, we find the data transferred by choosing the default parameter as well. We then calculate the fairness index and the results are tabulated in Table 11. It is observed that, if the TXOP and
required for satisfying the desired fairness objective. With these values, we compute the amount of data transfered. Also, we find the data transferred by choosing the default parameter as well. We then calculate the fairness index and the results are tabulated in Table 11. It is observed that, if the TXOP and  values are selected according to to (28), the fairness index can be made equal to unity. The analytical and simulation results for data transfered are listed in Table 12. It can be observed that, combined tuning of TXOP and CWmin according to (28) results in bit-based fairness, which means that the bits transferred
values are selected according to to (28), the fairness index can be made equal to unity. The analytical and simulation results for data transfered are listed in Table 12. It can be observed that, combined tuning of TXOP and CWmin according to (28) results in bit-based fairness, which means that the bits transferred

Table 10. Tuning of txop and .
.

Figure 6. Fairness index vs standard deviation of slow vehicle speed ( = 60 km/hr,
= 60 km/hr, 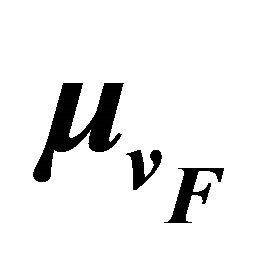 = 120 km/hr,
= 120 km/hr,  = 5 km/hr).
= 5 km/hr).

Table 11. Fairness index with default and optimal TXOP & 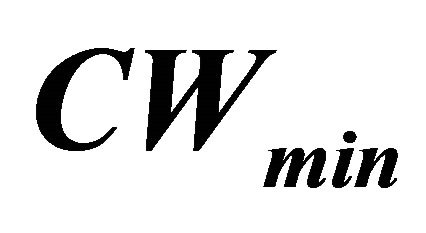 values for two classes (
values for two classes ( = 80 veh/km/lane).
= 80 veh/km/lane).

Table 12. Data transferred (individual and aggregate) with default and optimal TXOP values for two classes ( = 80 veh/km/lane).
= 80 veh/km/lane).
per vehicle are the same for all the classes of vehicles. In Figure 8 aggregate data transferred is plotted against μvS mean velocity of slow vehicle for the two cases considered in this paper: 1) tuning of TXOP alone and 2) combined tuning of TXOP and . It is observed that the aggregate data reduces as the
. It is observed that the aggregate data reduces as the  increases owing to the reduced residence time of slow vehicle in the coverage area of RSU. Further, it is observed that a joint tuning of TXOP and
increases owing to the reduced residence time of slow vehicle in the coverage area of RSU. Further, it is observed that a joint tuning of TXOP and  results in reduced aggregate data transferred, as compared to the case of tuning TXOP alone
results in reduced aggregate data transferred, as compared to the case of tuning TXOP alone
6. Conclusion
This paper proposes schemes to mitigate an unfairness problem that occurs among vehicles of distinct mean velocities in vehicle-to-infrastructure (V2I) networks used for drive-thru Internet applications. A vehicle moving with higher velocity has less chance to communicate with the Road Side Unit (RSU), as compared to the slow moving vehicle, due to its shorter residence time in the coverage area of RSU. This results in the degradation in the amount of data communicated by fast moving vehicles. The proposed schemes are are based on, assigning transmission opportunity (TXOP) limits to vehicles according to their mean velocities. Assuming a

Figure 7. Ratio of data transferred per node vs standard deviation of slow vehicle speed ( = 60 km/hr,
= 60 km/hr,  = 120 km/hr,
= 120 km/hr,  = 5 km/hr).
= 5 km/hr).

Figure 8. Aggregate data transferred vs mean velocity of slow station (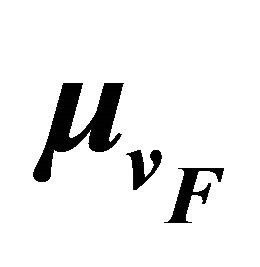 = 120 km/hr and
= 120 km/hr and  = 80,
= 80, 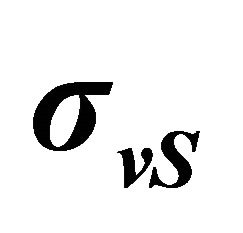 =
=  = 5 km/hr).
= 5 km/hr).
multi lane V2I network in which lane i is used by vehicles of mean velocity ,
,  , an analytical model was presented to compute the data transferred by vehicles belonging to class
, an analytical model was presented to compute the data transferred by vehicles belonging to class ,
, . Using Jain’s fairness index, TXOP limits required to ensure fairness, in the sense of equal chance of communicating with RSU, were determined. The effect of combined tuning of both TXOP and
. Using Jain’s fairness index, TXOP limits required to ensure fairness, in the sense of equal chance of communicating with RSU, were determined. The effect of combined tuning of both TXOP and  is also evaluated. The results from the analytical model were validated by extensive simulations.
is also evaluated. The results from the analytical model were validated by extensive simulations.
REFERENCES
- G. Karagiannis, O. Altintas, E. Ekici, G. Heijenk, B. Jarupan, K. Lin and T. Weil, “Vehicular Networking: A Survey and Tutorial on Requirements, Architectures, Challenges, Standards and Solutions,” IEEE Communication Surveys & Tutorials, Vol. 13, No. 4, 2011, pp. 584-616. doi:10.1109/SURV.2011.061411.00019
- “ASTM-E2213, Standard Specification for Telecommunications and Information Exchange between Roadside and Vehicle Systems 5GHz Band Dedicated Short Range Communications (DSRC) Medium Access Control (MAC) and Physical Layer (PHY) Specifications, American Society for Testing and Materials (ASTM) Std.,” 2002.
- “IEEE 802.11p, Amendment to Standard for Information Technology-Telecommunications and Information Exchange Between Systems-Local and Metropolitan Area Networks-Specific requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer(PHY) Specifications-Amendment 7: Wireless Access in Vehicular Environment, IEEE Std. IEEE 802.11p, Version 2010,” 2010.
- J. Ott and D. Kutscher, “Drive-Thru Internet: IEEE 802.11b for ‘Automobile’ User,” INFOCOM 2004. 23rd Annual Joint Conference of the IEEE Computer and Communications Societies, Hong Kong, 7-11 March 2004, pp. 362-373.
- V. Bychkovsky, B. Hull, A. K. Miu, H. Balakrishnan and S. Madden, “A Measurement Study of Vehicular Internet Access Using in situ Wi-Fi Networks,” Proceedings of ACM MobiCom’06, Los Angeles, 24-29 September 2006, pp. 50-61.
- G. Bianchi, “Performance Analysis of the IEEE 802.11 Distributed Coordination Function,” IEEE Journal on Selected Areas in Communications, Vol. 18, No. 3, 2000, pp. 535-547.
- “IEEE 802.11e/D4.0, Draft Supplement to Part 11: Wireless LAN MAC and PHY Specifications: MAC Enhancements for Quality of Service (QoS),” November 2005.
- F. Peng, H. M. Alnuweiri and V. C. M. Leung, “Analysis of Burst Transmission in IEEE 802.11e Wireless LANs,” Proceedings of the IEEE ICC’06, Vol. 2, 2006, pp. 535- 539.
- G. Y. Min, J. Hu and M. E. Woodward, “Modeling and Analysis of TXOP Differentiation in Infrastructure-Based WLANs,” Computer Networks, Vol. 55, No. 11, 2011, 2545-2557. doi:10.1016/j.comnet.2011.04.015
- J. Y. Lee, H. Y. Hwangy, J. Shin, and S. Valaee, “Distributed Optimal TXOP Control for Throughput Requirements in IEEE 802.11e Wireless LAN,” IEEE Personal Indoor Mobile Radio Communication Symposium (PIMRC), Toronto, 11-14 September 2011, pp. 935-939.
- E. Karamad and F. Ashtiani, “A Modified 802.11-Based MAC Scheme to Assure Fair Access for Vehicle-toRoadside Communications,” Computer Communications, Vol. 31, No. 12, 2008, pp. 2898-2906. doi:10.1016/j.comcom.2008.01.030
- V. P. Harigovindan, A. V. Babu and L. Jacob, “Ensuring fair Access in IEEE 802.11p-Based Vehicle-to-Infrastructure Networks,” EURASIP Journal on Wireless Communications and Networking, 2012, 168.
- X. Chen, H. H. Refai and X. Ma, “On the Enhancements to IEEE 802.11 MAC and their Suitability for SafetyCritical Applications in VANET,” Wireless Communications and Mobile Computing, Vol. 10, No. 9, 2010, pp. 1253-1269. doi:10.1002/wcm.674
- X. M. Ma, X. B. Chen and H. H. Refai, “Performance and Reliability of DSRC Vehicular Safety Communication: A Formal Analysis,” EURASIP Journal on Wireless Communications and Networking, Vol. 2009, Article ID: 969164, 13 Pages.
- T. H. Luan, X. H. Ling and X. M. (Sherman) Shen, “MAC Performance Analysis for Vehicle-to-Infrastructure Communication,” Proceedings of Wireless Communications and Networking Conference (WCNC), Sydney, 18-21 April 2010, pp. 1-6.
- T. H. Luan, X. H. Ling and X. M. (Sherman) Shen, “MAC in Motion: Impact of Mobility on the MAC of Drive-Thru Internet,” IEEE Transaction on Mobile Computing, Vol. 11, No. 2, 2011, pp. 305-319.
- J. H. He, Z. Y. Tang, T. O’Farrell and T. M. Chen, “Performance Analysis of DSRC Priority Mechanism for Road Safety Applications in Vehicular Networks,” Wireless Communications and Mobile Computing, Vol. 11, No. 7, 2011, pp. 980-990. doi:10.1002/wcm.821
- M. I. Hassan, H. L. Vu and T. Sakurai, “Performance Analysis of the IEEE 802.11 MAC Protocol for DSRC with and without Retransmissions,” IEEE International Symposium on a World of Wireless Mobile and Multimediab Networks, Montreal, 14-17 June 2010, pp. 1-8.
- W. L. Tan, W. C. Lau and O. Yue, “Modeling Resource Sharing for a Road-Side Access Point Supporting Drive- Thru Internet,” Proceedings of ACM VANET, Beijing, 25 September 2009, pp. 33-42.
- W. L. Tan, W. C. Lau, O. Yue and T. H. Hui, “Analytical Models and Performance Evaluation of Drive-Thru Internet Systems,” IEEE Journal on Selected Areas in Communications, Vol. 29, No. 1, 2011, pp. 207-222.
- S.-T. Sheu, Y.-C. Cheng and J.-S. Wu, “A Channel Access Scheme to Compromise Throughput and Fairness in IEEE 802.11p Multi-Rate/Multi-Channel Wireless Vehicular Networks,” IEEE 71st Vehicular Technology Conference, Taipei, 16-19 May 2010, pp. 1-5.
- W. Alasmary and W. Zhuang, “Mobility Impact in IEEE 802.11p Infrastructure Less Vehicular Networks,” Ad Hoc Networks, Vol. 10. No. 2, 2010, pp. 222-230. doi:10.1016/j.adhoc.2010.06.006
- L. Xie, Q. Li, W. Mao, J. Wu and D. Chen, “Achieving Efficiency and Fairness for Association Control in Vehicular Networks,” 17th IEEE International Conference on Network Protocols, 13-16 October 2009, Princeton, pp. 324-333.
- H. Wu, R. M. Fujimoto, G. F. Riley and M. Hunter, “Spatial Propagation of Information in Vehicular Networks,” IEEE Transactions on Vehicular Technology, Vol. 58, No. 1, 2009, pp. 420-431. doi:10.1109/TVT.2008.923689
- R. P. Roess, E. S. Prassas and W. R. Mcshane, “Traffic Engineering,” 3rd Edition, Pearson Prentice Hall, Upper Saddle River, 2004.
- R. Jain, W. Hawe and D. Chiu, “A Quantitative Measure of Fairness and Discrimination for Resource Allocation in Shared Computer Systems,” DEC Research Report TR- 301, September 1984.
NOTES
*Some part of this work was presented at 2012 ACM International Conference on Advances in Computing, Communications and Informatics (ICACCI-2012), Chennai, India.

