Journal of Applied Mathematics and Physics
Vol.03 No.10(2015), Article ID:60686,11 pages
10.4236/jamp.2015.310156
Existence and Multiplicity of Solutions for Quasilinear p(x)-Laplacian Equations in RN
Honghong Qi, Gao Jia
College of Science, University of Shanghai for Science and Technology, Shanghai, China
Email: qihonghong618@126.com, gaojia89@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 September 2015; accepted 25 October 2015; published 28 October 2015
ABSTRACT
We establish some results on the existence of multiple nontrivial solutions for a class of p(x)-Lap- lacian elliptic equations without assumptions that the domain is bounded. The main tools used in the proof are the variable exponent theory of generalized Lebesgue-Sobolev spaces, variational methods and a variant of the Mountain Pass Lemma.
Keywords:
p(x)-Laplacian Operator, Generalized Lebesgue-Sobolev Spaces, Variational Method, Multiple Solutions

1. Introduction
The study of differential and partial differential equations involving variable exponent conditions is a new and interesting topic. The interest in studying such problem was stimulated by their applications in elastic mechanics and fluid dynamics. These physical problems were facilitated by the development of Lebesgue and Sobolev spaces with variable exponent.
The existence and multiplicity of solutions of
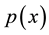 -Laplacian problems have been studied by several authors (see for example [1] [2] , and the references therein).
-Laplacian problems have been studied by several authors (see for example [1] [2] , and the references therein).
In [3] , A. R. EL Amrouss and F. Kissi proved the existence of multiple solutions of the following problem
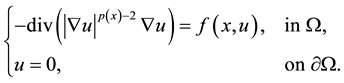 (1)
(1)
Also Xiaoyan Lin and X. H. Tang in [4] studied the following quasilinear elliptic equation
 (2)
(2)
and they proved the multiplicity of solutions for problem (2) by using the cohomological linking method for cones and a new direct sum decomposition of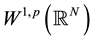 .
.
In this paper, we consider the following problem
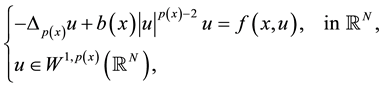 (3)
(3)
where
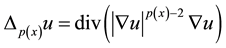 is the
is the
 -Laplacian operator;
-Laplacian operator;
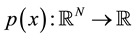 is a Lipschitz continuous function with
is a Lipschitz continuous function with
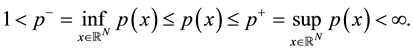
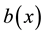 is a given continuous function which satisfies
is a given continuous function which satisfies
(B0)
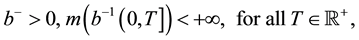
here m is the Lebesgue measure on RN.
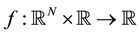 is a Carathéodory function satisfying the subcritical growth condition
is a Carathéodory function satisfying the subcritical growth condition
(F0)
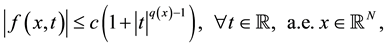
for some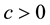 , where
, where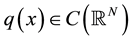 ,
,
 ,
,


Define the subspace

and the functional

where
Clearly, in order to determine the weak solutions of problem (3), we need to find the critical points of functional Φ. It is well known that under (B0) and (F0), Φ is well defined and is a C1 functional. Moreover,

for all
If



Set

This paper is to show the existence of nontrivial solutions of problem (3) under the following conditions.
(F1)

where

(F2) There exist



(F3) There exist



for a.e.
(F4)





We have the following results.
Theorem 1.1. If


Theorem 1.2. Assume




This paper is divided into three sections. In the second section, we state some basic preliminary results and give some lemmas which will be used to prove the main results. The proofs of Theorem 1.1 and Theorem 1.2 are presented in the third section.
2. Preliminaries
In this section, we recall some results on variable exponent Sobolev space


Let


For

Define the variable exponent Sobolev space:

which is endowed with the norm

It can be proved that the spaces


Proposition 2.1. [10] [11] Let

Then we have
1) For

2)

3)

4)

For




We have the following generalized Hölder type inequality.
Proposition 2.2. [9] [12] For any



We consider the case that


Then



Similar to the Proposition 2.1, we have
Proposition 2.3. [13] The functional


has the following properties:
1)
2)

3)

Lemma 2.4. [13] If

1) we have a compact embedding
2) for any measurable function





Now, we consider the eigenvalues of the p(x)-Laplacian problem

For any


For all

then



where

Define

We denote by



Define




Lemma 2.5. For all



Proof. Let


On the other hand, since the functional







Lemma 2.6.

Proof. From Lemma 2.5, we have

Since

so we have


Thus we get


Similarly, if





On the other hand, it is easy to see that

Now, we consider the truncated problem

where

We denote by


Lemma 2.7.
1) If



2) The mappings

Lemma 2.8. All solutions of


Proof. Define


where


Let u be a solution of


we have

By virtue of Proposition 2.3, we have




Similarly, the nontrivial critical points of the functional


3. Proof of Main Results
3.1. Proof of Theorem 1.1
To derive the Theorem 1.1, we need the following results.
Proposition 3.1. Φ is coercive on E.
Proof. Put

From (F1) we have, for any


By contradiction, let



Putting





Consequently,



Set

then,

From (6), (F1) and Lemma 2.6, we deduce that

This is a contradiction. Therefore, Φ is coercive on E. ,
Proposition 3.2. Assume




Proof. From (F2), there is a constant


From (F0) and


By (7) and (8), we get

For


Since


Thus the proposition follows. ,
Proof of Theorem 1.1. From Proposition 3.1, we know Φ is coercive on E. Since Φ has a global minimizer




3.2. Proof of Theorem 1.2
To find the properties of the p(x)-Laplacian operators, we need the following inequalities (see [10] ).
Lemma 3.3. For



Proposition 3.4. Assume (F0), and let









Proof. Let



Let us denote by


From Lemma 3.3, we have


Recalling that


and so,

On the other hand, by (11) and


Thus,

Combining Hölder’s inequality and Sobolev embedding, we deduce that

Let us consider the sets

From Lemma 3.3, we get


Applying again Hölder’s inequality,

where

and

Then,

From (12) and (13), we have

By (15)-(17), we obtain

(12) and (14) imply that

From (18) and (19),



Combined with Lebesgue’s dominated convergence theorem, we get

By (20) and


Proposition 3.5. Assume (F0), and let




Proof. From (F0), we have


Assume that



Since



Proposition 3.6. Assume




Proof. From Proposition 3.4, we have

By Lemma 2.4, we get

On the other hand, Lebesgue’s dominated convergence theorem and the weak convergence of


Moreover, since



Therefore, by virtue of the definition of weak convergence, we obtain

By (23)-(25), we have

By (22) and (26), we get

Then combining Lemma 3.3, we obtain

which imply that

Proposition 3.7. There exist





Proof. The conditions (F0) and (F4) imply that

For


By the condition (F0), it follows

from Lemma 2.4, which implies the existence of


Using (28) and Proposition 2.1, we deduce

Combining (27), it results in that

here




Since




,
Proposition 3.8. If




Proof. From the condition (F3), we get

For



Since

,
Proof of Theorem 1.2. According to the Mountain Pass Lemma, the functional







Similarly, for functional
Acknowledgements
This work has been supported by the Natural Science Foundation of China (No. 11171220) and Shanghai Leading Academic Discipline Project (XTKX2012) and Hujiang Foundation of China (B14005).
Cite this paper
HonghongQi,GaoJia, (2015) Existence and Multiplicity of Solutions for Quasilinear p(x)-Laplacian Equations in RN. Journal of Applied Mathematics and Physics,03,1270-1281. doi: 10.4236/jamp.2015.310156
References
- 1. EI Hamidi, A. (2004) Existence Results to Elliptic Systems with Nonstandard Growth Conditions. Journal of Mathematical Analysis and Applications, 300, 30-42.
http://dx.doi.org/10.1016/j.jmaa.2004.05.041 - 2. Mihailescu, M. (2007) Existence and Multi-plicity of Solutions for a Neumann Problem Involving the p(x)-Laplace Operator. Nonlinear Analysis, 67, 1419-1425.
http://dx.doi.org/10.1016/j.na.2006.07.027 - 3. EI Amrouss, A.R. and Kissi, F. (2013) Multiplicity of Solutions for a General p(x)-Laplacian Dirichlet Problem. Arab Journal of Mathematics and Mathematical Sciences, 19, 205-216.
http://dx.doi.org/10.1016/j.ajmsc.2012.09.006 - 4. Lin, X.Y. and Tang, X.H. (2013) Existence of Infinitely Many Solutions for p-Laplacian Equations in RN. Nonlinear Analysis, 92, 72-81.
http://dx.doi.org/10.1016/j.na.2013.06.011 - 5. Diening, L. (2004) Riesz Potential and Sobolev Embeddings on Generalized Lebesgue and Sobolev Spaces and . Mathematische Nachrichten, 268, 31-43.
http://dx.doi.org/10.1002/mana.200310157 - 6. Edmunds, D.E. and Rákosnik, J. (2002) Sobolev Embeddings with Variable Exponent II. Mathematische Nachrichten, 246-247, 53-67.
http://dx.doi.org/10.1002/1522-2616(200212)246:1<53::AID-MANA53>3.0.CO;2-T - 7. Fu, Y.Q. (2007) Existence of Solu-tions for p(x)-Laplacian Problem on an Unbounded Domain. Topological Methods in Nonlinear Analysis, 30, 235-249.
- 8. Canino, A. (1995) Multiplicity of Solutions for Quasilinear Elliptic Equations. Topological Methods in Nonlinear Analysis, 6, 357-370.
- 9. Fan, X.L. and Zhao, D. (2001) On the Spaces and . Journal of Mathematical Analysis and Applications, 263, 424-446.
http://dx.doi.org/10.1006/jmaa.2000.7617 - 10. Fan, X.L. and Han, X.Y. (2004) Existence and Multiplicity of Solutions for p(x)-Laplacian Equations in RN. Nonlinear Analysis, 59, 173-188.
http://dx.doi.org/10.1016/j.na.2004.07.009 - 11. Musielak, J. (1983) Orlicz Spaces and Modular Spaces. Lecture Notes in Mathematics, Springer-Verlag, Berlin.
- 12. Kovácik, O., Rákosnik, J. (1991) On Spaces and . Czechoslovak Mathematical Journal, 41, 592-618.
- 13. Alves, C.O. and Liu, S.B. (2010) On Superlinear p(x)-Laplacian Equations in RN. Nonlinear Analysis, 73, 2566-2579.
http://dx.doi.org/10.1016/j.na.2010.06.033

