Received 12 October 2014; revised 7 November 2014; accepted 2 December 2014

ABSTRACT

A kind of novel three-party quantum secure direct communication protocol is proposed with the correlation of two-particle entangled state. In this scheme the qubit transmission forms a closed loop and every one of the three participants is both a receiver and a sender of particle sequences in the bidirectional quantum channels. Each party implements the corresponding unitary operations according to its secret bit value over the quantum channels and then extracts the other two parties’ unitary operations by performing Bell measurements on the encoded particles. Thus they can obtain the secret information simultaneously. Finally, the security analysis shows that the present three-party scheme is a secure protocol.

Keywords:

Quantum Information, Quantum Cryptographic Protocol, Quantum Secure Direct Communication, Bell States

1. Introduction

Quantum key distribution (QKD) is based on quantum mechanics and has the unconditional security, in which all legitimate users can distribute a shared key beforehand to make secure communications. Different from QKD, quantum secure direct communication (QSDC), another important application of quantum cryptography, can allow the messages to be read out after qubit transmission and then exchange the secret information between all parties directly without distributing a shared secret key.

In 2002, Long et al. [1] presented the first QSDC protocol by using EPR entangled states. Then Beige et al. [2] proposed a QSDC scheme with the exchange of single photons. In the same year, Boström and Felbinger [3] proposed a deterministic secure direct communication scheme named “ping-pong” protocol based on two-pho- ton entangled states, which was improved by Li et al. [4] . Deng et al. [5] proposed two-step quantum direct communication protocol using the EPR pair block. However, the transmission of secret messages is unidirectional in QSDC. Then Nguyen [6] proposed a kind of protocol called quantum dialogue. Later, Jin et al. [7] proposed a three-party quantum secure direct communication based on the GHZ states, which was improved by Man et al. [8] . Wang et al. [9] proposed a three-party QSDC scheme with EPR pairs, and their protocol was improved on the quantum channels and the efficiency by Chong et al. [10] . Unfortunately, in 2013, Yin et al. [11] pointed out that [9] [10] can leak out the secret messages of the legitimate users with the classical correlation or information leakage [12] . In the same year, we [13] proposed an efficient quantum secure communication with two-photon entanglement.

In this paper, we propose a novel three-party QSDC protocol by using the idea of quantum dense coding on the two-particle EPR pair. The three parties in our scheme are peer entities and they transmit the particle sequences each other synchronously in a closed loop of qubit transmission. One party can obtain the other two parties’ secret messages through performing the joint measurement on the encoded particles. The rest of our scheme is structured as follows. Section 2 describes the whole protocol in detail. Section 3 analyzes the security of this protocol. Finally, Section 4 gives a conclusion briefly.

2. Description of the Present Protocol

The four Bell states can be written as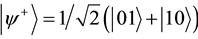, , 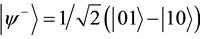,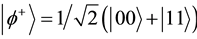. Where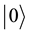, 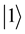are the up and down eigenstates of Pauli operator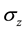. Let

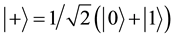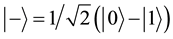,. Then 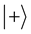and are the eigenstates of Pauli operator.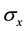

Suppose, and 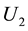are three unitary operations, That is, , and. An EPR pair can be transformed to another EPR pair if we perform the unitary operation or on the first qubit and or on the second qubit. In this paper, we take as the initial state and the transformation rule can be shown in Table 1.

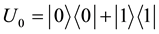Now, we suppose Alice, Bob, and Charlie as the three parties in our scheme. Let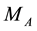, and denote their secret messages to be exchanged respectively. That is,

where, and. The three parties agree that they take the corresponding unitary operation according to their secret bit value. If the encoded particle is the first qubit of initial state, the rule is the following

(1)

If the encoded particle is the second qubit, the rule is the following

(2)

Next, we describe this protocol in detail.

Step 1. Alice/Bob/Charlie prepares states and takes two particles 1 and 2 from each entangled state to form two single particle sequences which can be denoted as. Moreover, each party chooses enough decoy photons from randomly and inserts them into their own two sequences. After that, Alice sends the mixed sequences and to Bob and Charlie respectively; Bob sends the mixed and to Charlie and Alice respectively; Charlie sends the mixed and to Alice and Bob respectively.

Step 2. After confirming (Bob, Charlie)/(Charlie, Alice)/(Alice, Bob) has received the mixed sequences, Alice/Bob/Charlie publishes the positions and the measurement basis or of the decoy particles. Then they check the quantum channels by presenting the measurement results. If the error rate exceeds the threshold, the protocol is discarded; otherwise, it will go to the next step.

Step 3. After picking out the decoy particles, Bob/Charlie/Alice performs the unitary operations on according to the rule (1). Charlie/Alice/Bob performs the unitary operations on according to the rule (2). The encoded sequences can be written as and, respectively. For the next security check of quantum channels, they insert randomly enough into their own sequences. Next, (Bob, Charlie) return which contain decoy particles to Alice respectively; (Charlie, Alice) return which contain decoy particles to Bob respectively; (Alice, Bob) return which contain decoy particles to Charlie respectively.

Step 4. After confirming that Alice/Bob/Charlie has received the mixed two sequences, the other two parties announce the positions and the corresponding measurement basis of the decoy particles. Then they check the security of quantum channels by comparing the measurement results of the decoy particles. If the error rate does not meet the requirement, the three parties abort the protocol; otherwise, they continue it.

Step 5. Alice/Bob/Charlie first picks out the decoy particles. Now, each party has two encoded sequences and performs Bell measurement orderly on the corresponding photon pairs in this two sequences, for instance, Alice performs Bell measurement on the EPR pairs in and. According to Table 1, each party can obtain the other two parties’ operation and then extract the secret messages from rules (1) and (2). Thus, three parties realize the information exchange.

From the above steps, we can see the qubit transmission forms a closed loop and every party sends or receives particles simultaneously. For conciseness, we take for example and only consider Alice obtains

and. Suppose, Alice first prepares. She sends particles 1 and 2 to Bob and Charlie

respectively. Bob performs on particle 1 from rule (1). Charlie performs on particle 2 from rule (2). Then Bob and Charlie return particles 1, 2 to Alice. Alice performs Bell measurement on the two particles and the measurement results must be. According to Table 1, Alice can know Bob’s and Charlie’s operation are and respectively. Thus she obtains.

3. Security Analysis

Now we analyze the security of our scheme. From the five steps, we can see that there must be a security check over quantum channels when one party sends a particle sequence to another party. On the other hand, the decoy particles are chosen from randomly. Thus, if Eve is an evil eavesdropper who wants to obtain the secret messages to be exchanged between the three parties, one of attack strategies that she may takes is the intercept-resend attack. For example, Eve can intercept the particles which are sent from Alice to Bob and resend them to Bob after she has some useful information by means of measurement method. When Eve captures the particles in the quantum channel, she replaces her own particles and resends them. However, since the decoy photons are randomly inserted into the sequence, Eve cannot know the positions and the corresponding measurement basis of these particles before the sender publishes the relevant information in the classical channels. Suppose is the number of decoy particles, then the probability that Eve could not been detected is. In fact, this kind of detection method is same with that in BB84 protocol. Therefore, Eve cannot steal any valuable information of shared secret key by this kind of attack strategies. Another attack strategy Eve may take is the entangle-measure attack. That is, Eve prepares an ancillary particle in the initial state. When she intercepts the qubits which are propagated from one party to another party, Eve makes the ancilla interact unitarily with these qubits. After that she sends them to the receiver and captures them again when the encoded particles are gone back. In this way Eve may obtain some information about the secret messages of the participants. Next, we will show that she cannot gain any secret information if Eve want to avoid that no errors are to occur. She adds the particle in the eavesdropping phase and performs a unitary operation on and the intercepted particle. Thus we have

Then the whole system is in the state

where

If Eve wants to avoid any error, the following conditions should be satisfied

According to the above equations, we can have

On the other hand, in the security check step, the measurement basis are chosen from and randomly. So we also have the following for the basis

From the correlations of Bell states, the state can been written as

Then the whole quantum system is in the following state

Similarly, from the above formula and the correlations of, we can know that the measurement results and must not exist under the condition that no errors are to occur. Thus the following equation can been obtained. Therefore the quantum system is in the state

That is, regardless of what the legitimate users take the measurement basis, the eavesdropper Eve cannot extract any useful information of the secret messages by observing the ancillary particle. Then our scheme is secure according to the above analysis and discussion.

4. Conclusion

In this paper, we propose a three-party quantum secret direct communication protocol with the bidirectional qubit transmission. In the whole process, we can see that all the parties form a return qubit circuit and they are peer entities. The three parties can exchange their own secret messages by using Bell measurement and unitary operations over the quantum channels. This scheme has a novel characteristic for the quantum return circuit and the member equivalence. However, the security discussion is based on the condition of ideal quantum channels. We have not considered the actual physical environment. In the quantum channel, noise and loss cannot be ignored with the particle transmission because they reduce the efficiency of quantum communication and increase the risk of information leakage. With the existing technologies, it has become more difficult to study such quantum communication protocols. We hope this problem can be solved in future research.

Acknowledgements

This work was supported by the Shandong Provincial Natural Science Foundation (No. ZR2013FQ011), the Project of Shandong Province higher Educational Science and Technology Program (No. J13LN60), Technology Development Projects of Tai’an (No.20140629-2) and Project of Taishan University Doctoral Fund (Y-01-2014020).

References