Open Access Library Journal
Vol.03 No.03(2016), Article ID:69080,7 pages
10.4236/oalib.1102399
A New method to calculate the Appropriateness measures of label Expressions in uncertainty model
Yang Liu, Xingfang Zhang*
School of Mathematical Sciences, Liaocheng University, Liaocheng, China

Copyright © 2016 by authors and OALib.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 27 February 2016; accepted 12 March 2016; published 16 March 2016

ABSTRACT
The appropriateness measure of label expression is a basal concept in uncertainty modelling based on label semantics theory for dealing with vague concepts. In the paper, the concept of disjunctive normal forms is presented. It is proved that each label expression is semantic equivalent to a disjunctive normal form. Further, a new method of calculating the appropriateness measures of label expressions is provided.
Keywords:
Epistemic Vagueness, Label Semantics, Random sets, Appropriateness measure, Disjunctive Normal form
Subject Areas: Mathematical Analysis

1. Introduction
It is well known that any concept in classical mathematics is established on a crisp set (i.e., Cantor set). Suppose a concept Q is defined by a non-empty set D, then we say the statement that a is Q, is true (or its truth value is 1) if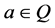 ; or else, it is false (or its truth value is 0). In other words, classical mathematics is established on classical logic or two-valued logic. However, for some propositions we cannot judge that they are true or false, such as the following propositions are not all classical propositions:
; or else, it is false (or its truth value is 0). In other words, classical mathematics is established on classical logic or two-valued logic. However, for some propositions we cannot judge that they are true or false, such as the following propositions are not all classical propositions:
1) A coin tossed will be heads;
2) John will be in New York tomorrow;
3) John with 30 hairs is a bandicoot;
4) John is a bandicoot.
There are various nonclassical propositions in real life. Lukasiewicz is first extended classical logic to three- valued logic as early as 1920. In 1933, A.N. Kolmogoroff presented the probability theory for dealing with a type of uncertainty called randomness [1] (such as the above nonclassical propositions (1) and (2)). Following that, probabilistic logic for dealing with random proposition was proposed by Nilsson [2] based on probability theory in 1986. The theory of fuzzy set was initialized by Zadeh via membership function in 1965 [3] - [5] for fuzzy concepts (such as concept of bandicoot in the above propositions (3) and (4)). Following that, many types of many-valued logic and fuzzy logic were presented, respectively, such as Lukasiewicz fuzzy logic [6] product fuzzy logic, L logic [7] [8] , possibilistic logic [9] , BL logic [10] , and MTL logic [11] .
Although multi-valued logics, fuzzy logic [12] - [19] and probabilistic logic are well developed in theory aspect, an actual interpretation of truth value of proposition is controversial. For example, Elkan and Watkins oppose fuzzy logics [20] - [22] , and claim that fuzzy logics have some disadvantages, e.g., it does not hold the law of excluded middle (i.e.,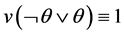 ) in classical logic, where
) in classical logic, where  denotes a proposition;
denotes a proposition; 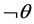 denotes its negation of proposition
denotes its negation of proposition ;
;  denotes disjunction; and
denotes disjunction; and 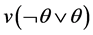 denotes the truth value of proposition
denotes the truth value of proposition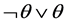 . Recently, the author of paper also discussed this problem [23] .
. Recently, the author of paper also discussed this problem [23] .
In fact, Zadeh’s approach is the extension of a concept by a fuzzy set which has a graded characteristic or membership function with values between 0 and 1. This allows for intermediate membership (values in (0, 1)) in vague concepts resulting in intermediate truth values for propositions involving vague concepts (fuzzy logic). The calculus for fuzzy set theory is truth-functional which means that the full complement of Boolean laws cannot all be satisfied [24] . Furthermore, fuzzy set theory and fuzzy logic adopt an epistemic view of vagueness. Considering the shortcoming of fuzzy logic, it was proposed to the probabilistic logic holding the law of excluded middle dealing with fuzzy (or vague) concepts from a point of view in these papers [25] - [29] . In 2004, Lawry also provided a framework for linguistic modelling for dealing with vague (i.e. fuzzy) concepts based on label semantics using probability theory and random set [30] . At present it has been well developed [31] - [35] which was called uncertainty modelling for vague concepts in the paper [34] . In the theory, the appropriateness measure of label expressions is a basal concept. Given the label expression, a pivotal step of calculating the appropriateness measures is to seek a set of subsets of label corresponding to the label expression. Note that it is complicated to the approach of calculating the appropriateness measures of label expression provided in these papers [31] - [35] . Therefore the paper will discuss this problem.
The rest of this paper is organized as follows. Some basic concepts on uncertainty modelling for vague concepts are recalled in Section 2. In Section 3, the concept of disjunctive normal forms is first presented; then it is proved that each label expression is semantic equivalent to a disjunctive normal form; finally, a new method of calculating the appropriateness measure of label expression is provided. At the end of this paper, a brief summary is given.
2. Preliminaries
Definition 1 (Label expressions). Given a finite set of labels LA the corresponding set of label expressions LE is defined recursively as follows:
・ If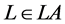 , then
, then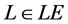 ;
;
・ If 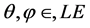 then
then 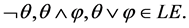
The mass function  on sets of labels then quantifies the agent’s belief that any particular subset of labels contains all and only the labels with which it is appropriate to describe x i.e.
on sets of labels then quantifies the agent’s belief that any particular subset of labels contains all and only the labels with which it is appropriate to describe x i.e. 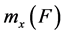 is the agent's subjective probability that
is the agent's subjective probability that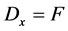 .
.
Definition 2 (Mass function on labels). 


Definition 3 (λ-mapping). 
・
・
・
・
Based on the λ mapping we then define 




Definition 4 (Appropriateness measure). The appropriateness measure defined by mass function 

Let Val be the set of valuation functions 










Definition 5.
・ 


・ 
・ θ is a tautology, if
・ θ is a contradiction, if
Theorem 6 (General properties of appropriateness measures). 
・ If 
・ 
・ If θ is a tautology, then
・ If θ is a contradiction, then
・ If 
・
・ For


We not find the proof of last property in Theorem 6 in these papers [30] - [35] . Therefore, now we provide it.
Proof. Without loss of generality, suppose
Thus we only need to prove that

We first prove that

Since for each









Thus the formula (3) is true.
Now we prove that for any









Therefore 
The theorem is proved.
3. Calculating of the appropriateness Measures
In the Section we first discuss the properties of valuation functions.
For convenience, we call each element in Label 











Note that 







Definition 7. A label expression θ is said to be a disjunctive normal form, if its form is
where 




Let

Lemma 8. For each






Proof. Let
On the one hand, 




On the other hand, let 







Lemma 9. Let label expression θ be a non-contradiction, and it contains atomic label expressions

i.e.,

where for each
satisfies that 





If

we call

as disjunctive normal form of θ, and it is denoted by
Proof. From Definition 5 we need to prove
It is evident that we only need to prove 
For 



that 
Contrarily, for 
By Lemma 8 we known that 



Thus
The theorem is proved.
By Lemma 9 and Definition 3 we easily gained the following Lemma.
Lemma 10. Let 


if
where for each
satisfies that 





Theorem 11. Let 


Proof. By Lemma 10 we have
It follows from Theorem 6 and the meaning of mapping



Exempla 12. Suppose


For 
It we write 
Thus we have
4. Conclusion
The paper manly provided a new method for calculating the appropriateness measures of label expressions. Based on the fact, each label expression is semantic equivalent to a disjunctive normal form.
Acknowledgements
This work was supported by national natural science foundation of China grant No.11471152 and No.61273044.
Cite this paper
Yang Liu,Xingfang Zhang, (2016) A New Method to Calculate the Appropriateness Measures of Label Expressions in Uncertainty Model. Open Access Library Journal,03,1-7. doi: 10.4236/oalib.1102399
References
- 1. Chen, L., Mu, Z.C. and Nan, B.F. (2015) Semantic Image Segmentation Based on Hierarchical Conditional Random Field Model. Journal of Computational Information Systems, 11, 527-534.
- 2. Nilsson, N. (1986) Probability Logic. Artificial Intelligence, 28, 71-78.
http://dx.doi.org/10.1016/0004-3702(86)90031-7 - 3. Zadeh, L.A. (1973) Outline of a New Approach to the Analysis of Complex Systems and Decision Processes. IEEE Transactions on Systems, Man and Cybernetics, 3, 28.
http://dx.doi.org/10.1109/TSMC.1973.5408575 - 4. Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353.
http://dx.doi.org/10.1016/S0019-9958(65)90241-X - 5. Zadeh, L.A. (1975) Fuzzy Logic and Approximate Reasoning. Synthese, 30, 407-428.
http://dx.doi.org/10.1007/BF00485052 - 6. Lukasiewicz, J. and Tarski, A. (1930) Untersuchungen über den Aussagenkalkül. Comptes Rendus des Séances de la Sociélé des Scierices et des Lettres des Varsovie Classe III, 23, 30-50.
- 7. Wang, G. and Zhou, H. (2009) Introduction to Mathematical Logic and Resolution Principle. 2nd Edition, Science Press Beijing, and Alpha Science International Limited, Oxford.
- 8. Wang, G. (1997) A Formal Deduction System of Fuzzy Propositional Calculation. Science in China Series E-Information Sciences, 42, 1041-1044.
- 9. Doubois, D. and Prade, H. (2001) Possibility Theory, Probability Theory and Multiple-Valued Logic. Annals of Mathematics and Artificial Intelligence, 32, 35-66.
http://dx.doi.org/10.1023/A:1016740830286 - 10. Hajek, P. (1998) Metamathematics of Fuzzy Logic. Kluwer Academic Publishers, London, 89-120.
http://dx.doi.org/10.1007/978-94-011-5300-3 - 11. Esteva, F. and Godo, L. (2001) Monoidal t-Norm Based Logic: Towards Logic for Left-Continuous t-Norms. Fuzzy Sets and Systems, 124, 271-288.
http://dx.doi.org/10.1016/S0165-0114(01)00098-7 - 12. Dubois, D. and Prade, H. (1988) An Introduction to Possibility and Fuzzy Logics. In: Smets, P., Mamdani, A., Dubois, D. and Prade, H., Eds., Non-Standard Logics for Automated Reasoning, Academic Press, London, 742-755.
- 13. Dubois, D. and Prade, H. (1990) Measuring Properties of Fuzzy Sets: A General Technique and Its Use in Fuzzy Query Evaluation. Fuzzy Sets and Systems, 38, 137-152.
http://dx.doi.org/10.1016/0165-0114(90)90146-W - 14. Dubois, D. and Prade, H. (1997) The Three Semantics of Fuzzy Sets. Fuzzy Sets and Systems, 90, 141-150.
http://dx.doi.org/10.1016/S0165-0114(97)00080-8 - 15. Dubois, D., Godo, L., Prade, H. and Esteva, F. (2005) An Information-Based Discussion of Vagueness. In: Cohen, H. and Lefebre, C., Eds., Handbook of Categorization in Cognitive Science, Elsevier Science, Amsterdam, 891-909.
http://dx.doi.org/10.1016/B978-008044612-7/50095-0 - 16. Li, L. and Zhang, J. (2010) Attribute Reduction in Fuzzy Concept Lattices Based on the T Implication Original Research Article Pages. Knowledge-Based Systems, 23, 497-503.
http://dx.doi.org/10.1016/j.knosys.2010.03.006 - 17. Miller, S. and John, R. (2010) An Interval Type-2 Fuzzy Multiple Echelon Supply Chain Model Original Research Article Pages. Knowledge-Based Systems, 23, 363-368.
http://dx.doi.org/10.1016/j.knosys.2009.11.016 - 18. Buckley, J., Siler, W. and Tucker, D. (1986) A Fuzzy Expert System. Fuzzy Sets and Systems, 20, 1-16.
http://dx.doi.org/10.1016/S0165-0114(86)80027-6 - 19. Egemen, A. and Telatar, Y.Z. (2010) Note-against-Note Two-Voice Counterpoint by Means of Fuzzy Logic Original Research Article. Knowledge-Based Systems, 23, 256-266.
http://dx.doi.org/10.1016/j.knosys.2010.01.007 - 20. Elkan, C. (1994) The Paradoxical Success of Fuzzy Logic. IEEE Expert, 9, 3-8.
http://dx.doi.org/10.1109/64.336150 - 21. Elkan, C. (1994) The Paradoxical Controversy over Fuzzy Logic. IEEE Expert, 9, 47-49.
http://dx.doi.org/10.1109/64.336150 - 22. Watkins, F.A. (1995) False Controversy: Fuzzy and Non-Fuzzy Faux Pas. IEEE Expert, 10, 4-5.
- 23. Zhang, X. (2011) Duality and Pseudo Duality of Dual Disjunctive Normal Forms. Knowledge-Based Systems, 24, 1033-1036.
http://dx.doi.org/10.1016/j.knosys.2011.04.017 - 24. Zadeh, L.A. (1975) The Concept of Linguistic Variable and Its Application to Approximate Reasoning, Part 2. Information Sciences, 8, 301-357.
http://dx.doi.org/10.1016/0020-0255(75)90046-8 - 25. Flaminio, T. and Godo, L. (2007) A Logic for Reasoning about the Probability of Fuzzy Events. Fuzzy Sets and Systems, 158, 625-638.
http://dx.doi.org/10.1016/j.fss.2006.11.008 - 26. Coletti, G. and Scozzafava, R. (2002) Probability Logic in a Coherent Setting. Kluwer Academic Publishers, London.
http://dx.doi.org/10.1007/978-94-010-0474-9 - 27. Fine, K. (1975) Vagueness, Truth and Logic. Synthese, 30, 265-300.
http://dx.doi.org/10.1007/BF00485047 - 28. Hailperin, T. (1996) Sentential Probability Logic. Associated University Presses, London.
- 29. Flaminioa, T. and Godo, L. (2007) A Logic for Reasoning about the Probability of Fuzzy Events. Fuzzy Sets and Systems, 158, 625-638.
http://dx.doi.org/10.1016/j.fss.2006.11.008 - 30. Lawry, J. (2004) A Framework for Linguistic Modeling. Artificial Intelligence, 155, 1-39.
http://dx.doi.org/10.1016/j.artint.2003.10.001 - 31. Lawry, J. (2006) Modelling and Reasoning with Vague Concepts. Springer, Berlin.
- 32. Lawry, J. (2008) Appropriateness Measures: An Uncertainty Model for Vague Concepts. Synthese, 161, 255-269.
http://dx.doi.org/10.1007/s11229-007-9158-9 - 33. Lawry, J. (2008) An Overview of Computing with Words Using Label Semantics. In: Bustince, H., Herrera, F. and Montero, J., Eds., Fuzzy Sets and Their Extensions: Representation, Aggregation and Models, Springer, Berlin, 65-87.
http://dx.doi.org/10.1007/978-3-540-73723-0_4 - 34. Lawry, J. and Tang, Y. (2009) Uncertainty Modelling for Vague Concepts: A Prototype Theory Approach. Artificial Intelligence, 173, 1539-1558.
http://dx.doi.org/10.1016/j.artint.2009.07.006 - 35. Tang, Y. and Zheng, J. (2006) Linguistic Modelling Based on Semantic Similarity Relation amongst Linguistic Labels. Fuzzy Sets and Systems, 157, 1662-1673.
http://dx.doi.org/10.1016/j.fss.2006.02.014
NOTES
*Corresponding author.














































