Paper Menu >>
Journal Menu >>
 Spin Forms and Spin Interactions among Higgs Bosons, between Higgs Boson and Graviton ShaoXu Ren Institute of Physical Science and Engineering Tongji University, 200092, Shanghai, China Corresponding email: shaoxu-ren@hotmail.com Received 16 March 2016; accepted 25 April 2016; published 29 April 2016 ———————————————————————————————————– ———————————————————————————————————– Abstract This paper offers concrete spin matrix forms of 0spinzero particle, and shows the existent of the spin interactions among 0spin zero particles.It is obviously hoping to approach, on the most comprehensive level,to understand what really Higgs Boson is and what role-play HiggsBoson is acting in particle physics. As a "particle" of gravitational force, the spin interaction between0spin zero particle (Higgs Boson) and 2spin particle (Graviton) is given,which maybe a way that people would find Graviton in future. Keywords Higgs Boson; Graviton; Vacuum Bubble Pair; Spin Topological Space, STS; Casimir operator; right-hand 0spin zeroparticle; left-hand 0spin zero particle ———————————————————————————————————– ———————————————————————————————————– 1. Introduction Higgs particle is a fundamental particle predicted by the Standard Model, and confirmed by the Large HadronCollider at CERN.[1]Higgs particle could explain why thephoton has nomass while Wand ZBosons are very heavy in electron-weak theory, and endows Fermions such as electron, muon and tau particle and quarks with their masses.The intrinsic spin angular momentum of Higgs particle is0. In conventional quantum mechanics,the representation of spin zero particle is a zero-matrix of one dimensional space,this means,in fact, Higgs particle hasno matrix representation for itsspin property in the Standard Model.What a pity ! magical Higgs particle could create masses of the particles in universe, however, failing to write out its own non-trivial spin matrices. Zero is not nothing,zero spin is not non-twirling.From the pointviewof The Third Kind of Particles,TKP,[2] the angular momentum property of spin zero particle canbe expressed by infinite dimensional non-Hermitian matrices whichrelated to Vacuum Bubble Pair,VBP , Journal of Modern Physics, 2016, 7, 737-759 Published Online April 2016 in SciRes. http://www.scirp.org/journal/jmp http://dx.doi.org/10.4236/jmp.2016.78070 How to cite this paper: Ren, S.X. (2016) Spin Forms and Spin Interactions among Higgs Bosons, between Higgs Boson and Graviton. Journal of Modern Physics, 7, 737-759. http://dx.doi.org/10.4236/jmp.2016.78070  these pairs could be excited into 0spin particle formphase transitions of Vacuum Spin Particle,VSP, whose Casimir Operator is −1 42I0,less than zero. [3]( CasimirOperatorofHiggsparticleis02I0,of Graviton is 62I0) In conventional quantum mechanics, each particle has its own spin space: one spin prticle, one spin space; two spin particles,two spin spaces; .......; nspin particles, nspin spaces.These spin spaces are independent each other, and expressed by VV1⊗V2⊗V3⊗... ⊗Vn. This paper gives advice: Since the spin angularmomentumconstituents of every elementary particle are composed of the common series of math elements that based on the raising operatorsj 1; j,k i2; j,k −and lowering operatorsk −1; j,k –i2; j,k −, ( whichcomposeVBP,TKP ),then anewtypeof spin space,the so-called Spin Topological Space,STS ,[4] is established. All sorts of spin sparticles are attributed to this spin space, STS. In traditional views, there are no any spininteractions among spinzero particles. However, by means of STS concept, on the contrary, it is shown there are the spin interactions. 0Spin zero particle not only possesses spin phenomena but also appears out right-circumrotationand left-circumrotation, such kind of propertiesmay exist in Higgs Boson world of the Standard Model. Same reason for,there should be spin particle interactions between Higgs Boson and graviton, and spin interactions among gravitons,detecting gravitational force,after the interference effect of gravitational wave is comfirmed.[5] 2. Higgs Boson’s Spin angular Momentum matrices1l,2l,3l The mathematical structure of 1l,2l,3land 3 2l,1 2l2 2lare given in matrix series(1),(2),(3) shown below. They satisfy angular momentum commutation rules iljl−jlilikl(0.1) i,j,k1, 2, 3arecirculative Casimir Operator 2l1 2l2 2l3 2l0I0001I0(0.2) Using raising operator, lowering operator l1li2l;-l1l−i2l(0.3) Then (0.1) turns to 3ll−l3ll(0.4) 3l−l−−l3l−−l(0.5) l−l−−ll23l(0.6) What follows are the explicit spinmatrix representations of three generations (l1,2,3)of 0Boson, (Higgs Boson). 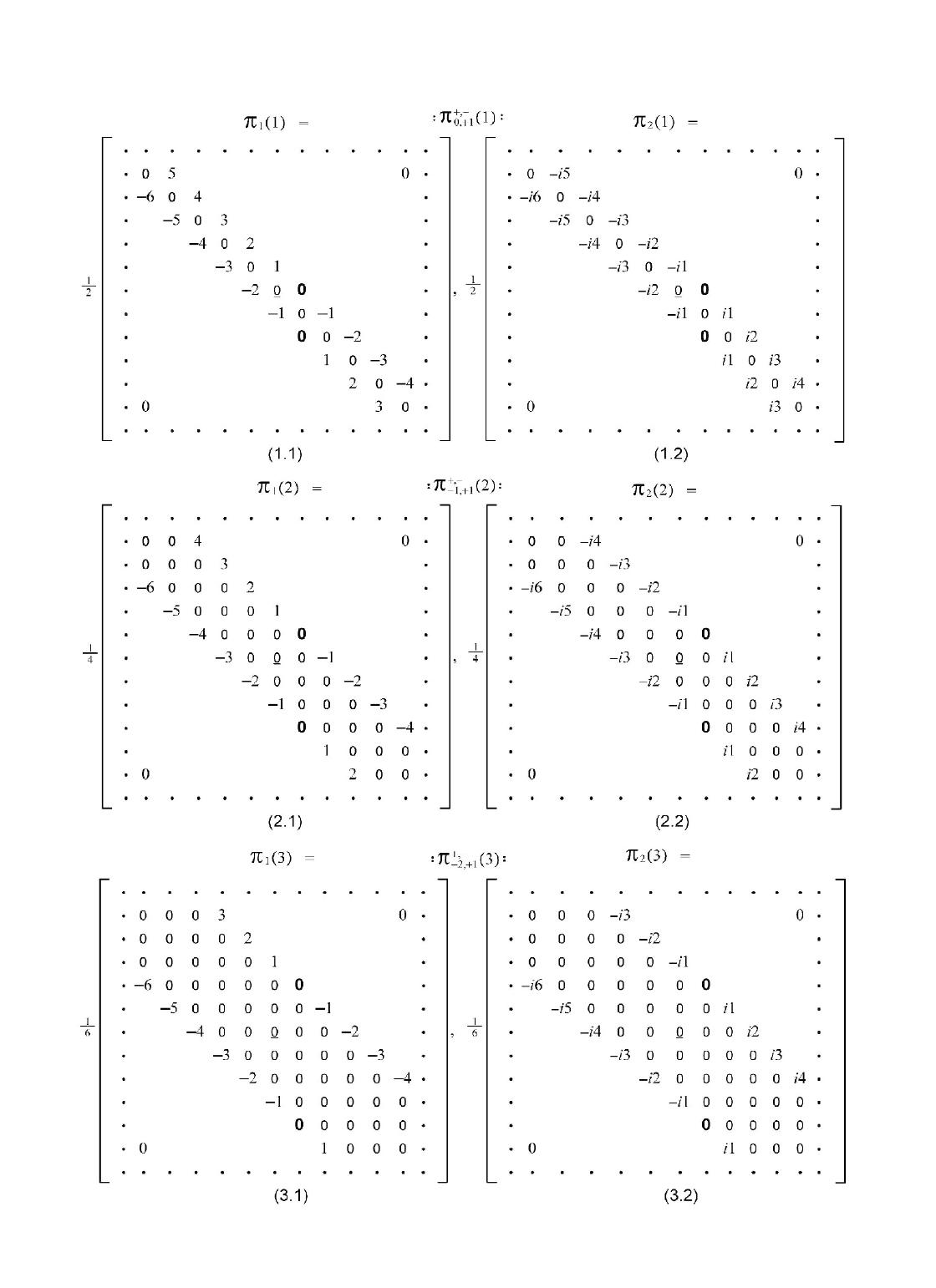 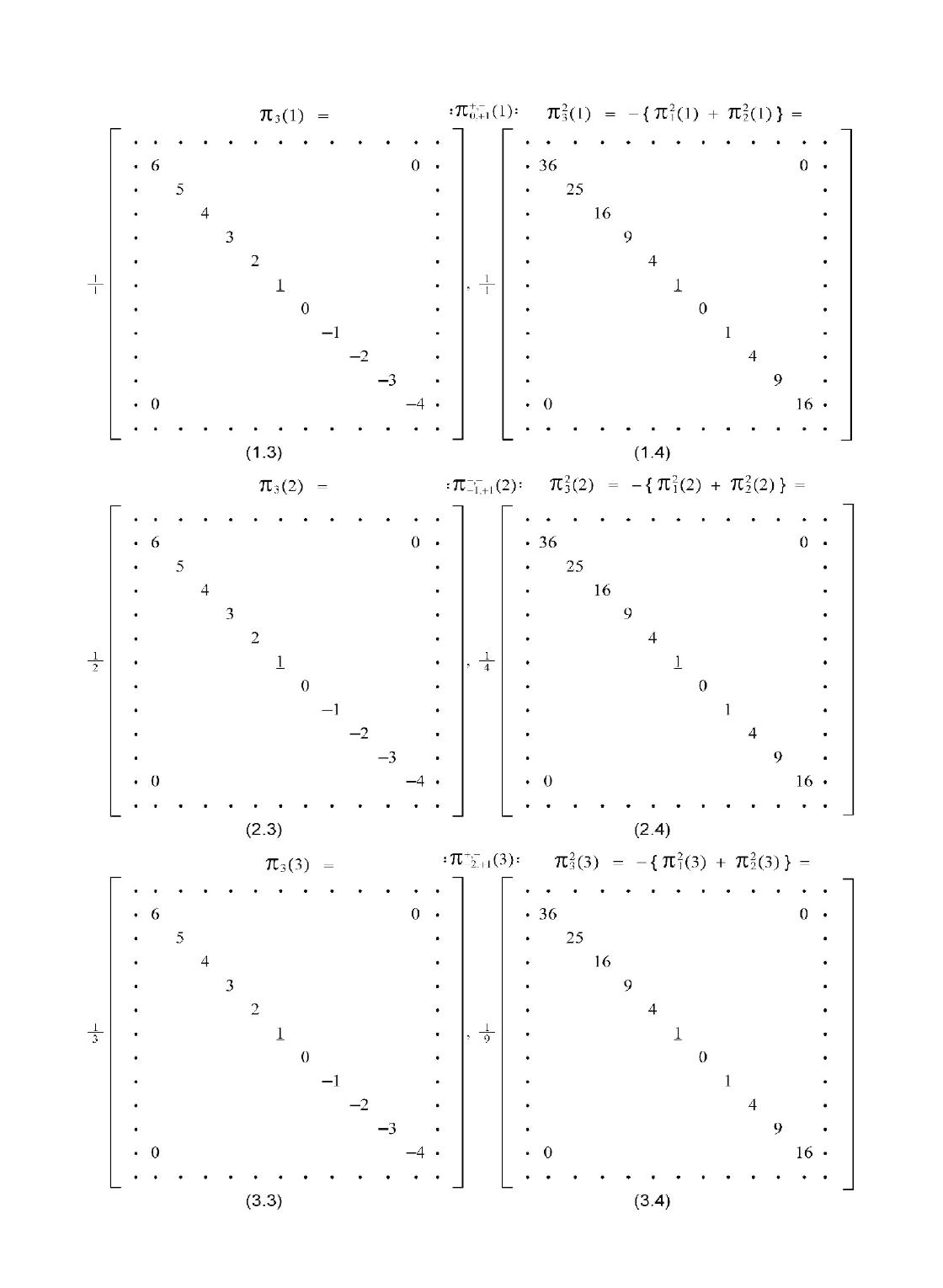  Be brief, in Spin Topological Space,STS,[4], the above spin matrices { (1.1), (1.2), (1.3);(2.1), (2.2), (2.3);(3.1), (3.2), (3.3) }ofHiggsBosoncanbe rewritten in the spin forms of (4.1),(4.2),(4.3) 0, 11{11,21,31} (4.1) −1,12{12,22,32} (4.2) −2,13{13,23,33} (4.3) For an example of 0, 11, now, (4.1) is denotedby (5.0): 0, 11{1;0, 11,2;0, 11,3;0, 11} (5.0) 1;0, 111 20 1 −11(5.1) 2;0, 111 2i 0 −1 −21(5.2) 3;0, 111 i{1;0, 112;0, 11−2;0, 111;0, 11}31 (5.3) 3. Spin Interactions between Two HiggsBosons a) First we deal with two-body systemthat compose of Higgs Boson a, aandHiggsBosonb,b.aand bare their spin angular momentum matrix operators.Then show a case of a spin coupling interaction (6.0) between aand b,the scalar products S2l, or Casimir operators of their three generations as follows S2lSlSl(6.0) Where Slalbl(7.0) Or S0, 1;−2, −110, 11−2, −11(7.1) S−1,1;−3,−12−1,12−3, −12(7.2) S−2,1;−4,−13−2,13−4, −13(7.3) After careful calculation, for S2(6.0),we have (8.0) S2lSlSl0I0(8.0) Or S0, 1;−2, −1 210I0(8.1) S−1,1;−3,−1 220I0(8.2) S−2,1;−4,−1 230I0(8.3) I0diag{...,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,...}(9.0) (8.0) and (8.1),(8.2),(8.3) show: there are no any effects of spin coupling bwtween two 0zero spin particles, aland bl.  b) How can we find no-trivial spin-coupling interactionrather than (8), by using augular momentum operators of 0zero spinparticle ? Actually there are two types of 0zerospinparticles,whichisawayto overcome the obstacle Assume 0zero spin particles 0, 11and −2, −11to be thought of as two right-hand spin particles,frmula (7.1) could be written as (10). ARS0, 1;−2, −110, 11−2, −11(10) Further the formula (8.1) is expressed as (11) ARI0ARS0, 1;−2, −1 210I0(11) On the other side,AL ⊙is markedas the adjoint counter of ARwith metric cofficient operator,then 0, 1 ⊙1and −2, −1 ⊙1are left-hand zero spin particles accordingly.we have AL ⊙S0, 1;−2, −1 ⊙10, 1 ⊙1−2, −1 ⊙1(12) We are now ready to take further our discussion of scalar product of right-hand-to-right-hand, ARI0AR(11),to psecudo-scalar product of left-hand-to-right-hand, AL ⊙AR(13), as follows ARI0ARAL ⊙AR(13) Here metric cofficient operator isselected as 010 100 001 (14) Attention: right-hand 0zero spin particles0, 11and −2, −11obey angular momentumcommutation rules of right-handed coordinate system; left-hand 0zero spin particles 0, 1 ⊙1and −2,−1 ⊙1obey angular momentumcommutation rules of left-handed coordinate system. For moreconcise, the symbols (15) are given in the futurediscussions ARj,k;r,s≡j,k1r,s1,3i,j≡3; i,j1(15)  c) Let us have a look at an example of psecudo-scalar product of left-hand-to-right-hand of spin zero particles, AL ⊙AR.Aftercareful calculation,we get two groups of 0spin interactions, Group-A and Group-B. By way of illustration, we shall refer to the feature B(1) of Group-B: Formulas (16.1) (16.2)and formulas (17.1), (17.2)are the third compoments of initial state iand final state fof psecudo-scalar spin interaction of the first generation spin particles(l1). Initial state 030, 1diag {...6, 5, 4, 3, 2,1,0,-1, -2, -3, -4,...}(16.1) 03−2, −1diag {...4, 3, 2, 1,0, -1, -2, -3, -4, -5, -6...}(16.2) Final state 030, −1diag {...5, 4, 3, 2, 1, 0,-1, -2, -3, -4, -5,...}(17.1) 13−2, 1diag {...5, 4, 3, 2, 1,0, -1, -2, -3, -4, -5,...}(17.2) And the conservation of the third compoment of spin angular momentums between initial state iand final state fis obtained as (18.0) 30, 1; −2, −130, −1; −2, 1(18.0) ininal sum of s.a.mfinal sum of s.a.m Where 30, 1; −2, −130, 13−2,−1(18.1) 30, −1; −2, 130, −13−2,1(18.2) And the conservation of psecudo-scalar spin interactionabout ininl state i and final state fis obtained as(19.0) LB,i(1) LB,f(1) LB(19.0) Where LB,i(1) BL,1 ⊙0,1; −2, −1BR,1 0,1; −2, −1(19.1) LB,f(1) BL,1 ⊙0,−1; −2, 1BR,1 0,−1; −2, 1(19.2) LB−2 diag {...102,8 2,6 2,4 2,2 2, 02,2 2,4 2,6 2,8 2,10 2, ,...}(20) What mentioned above isso-called fission of 0zero spin particles, refer to Fig4. Conservation (18.0) and conservation (19.0) imply that if initial state i and final state fexchange places, so-called fusion of other spinparticles is given, refer to Fig3. Fig1, Fig2 of Group-A are obtained by the analogy to those of Fig3, Fig4 of Group-B above.  A(3) 0−2, 1↖LA,f(3) 1 32LA↗−3,0 0A(3) A(2) 0−1, 1↖LA,f(2) 1 22LA↗−2,0 0A(2) A(1) 00,1↖LA,f(1) 1 12LA↗−1,0 0A(1) 1 0 fusions A A(3) −/6 −2,0 ↗LA,i(3) 1 32LA↖−3, 1/6 A(3) A(2) −/4 −1,0 ↗LA,i(2) 1 22LA↖−2, 1/4 A(2) A(1) −/2 0, 0↗LA,i(1) 1 12LA↖−1, 1/2 A(1) Fig1zero spin particles are formedby the fusions of other spin particles A(3) −/6 −2,0 ↖LA,f(3) 1 32LA↗−3, 1/6 A(3) A(2) −/4 −1,0 ↖LA,f(2) 1 22LA↗−2, 1/4 A(2) A(1) −/20, 0↖LA,f(1) 1 12LA↗−1, 1/2A(1) fissions A 1 0 A(3) 0−2, 1↗LA,i(3) 1 32LA↖−3,0 0A(3) A(2) 0−1, 1↗LA,i(2) 1 22LA↖−2,0 0A(2) A(1) 00,1↗LA,i(1) 1 12LA↖−1,0 0A(1) Fig2other spin particles are released by the fissions of zerospinparticles LA,f(3) ≡AL,3 ⊙−2,0 ; −3, 1AR,3 −2, −1; −3, 1(21.1) LA,i(3) ≡AL,3 ⊙−2, 1; −2, 1AR,3 0, 1; −3,0 (21.2) LA,f(2) ≡AL,2 ⊙−1,0 ; −2, 1AR,2 −1, −1; −2, 1(22.1) LA,i(2) ≡AL,2 ⊙−1, 1; −1, 1AR,2 −1, 1; −2,0 (22.2) LA,f(1) ≡AL,1 ⊙0, 0;−1, 1AR,1 0, 0;−1, 1(23.1) LA,i(1) ≡AL,1 ⊙0,1; −1,0 AR,1 0,1; −1,0 (23.2) LA−2 diag {...112,9 2,7 2,5 2,3 2, 12,1 2,3 2,5 2,7 2,9 2, ,...}(24)  B(3) 0−2, 1↖LB,f(3) 1 32LB↗−4, 10B(3) B(2) 0−1, 1↖LB,f(2) 1 22LB↗−3, −10B(2) B(1) 00,1↖LB,f(1) 1 12LB↗−2, −10B(1) 1−1 fusions B B(3) −/3 −2,−1↗LB,i(3) 1 32LB↖−4, 1/3B(3) B(2) −/2 −1,−1↗LB,i(2) 1 22LB↖−3, 1/2 B(2) B(1) 00,−1↗LB,i(1) 1 12LB↖−2, 11B(1) Fig3zero spin particles are formedby the fusions of other spin particles B(3) −/3 −2, −1↖LB,f(3) 1 32LB↗−4, 1/3 B(3) B(2) −/2 −1, −1↖LB,f(2) 1 22LB↗−3, 1/2 B(2) B(1) 00,−1↖LB,f(1) 1 12LB↗−2, 11∗B(1) fissions B 1−1 B(3) 0−2, 1↗LB,i(3) 1 32LB↖−4, −10B(3) B(2) 0−1, 1↗LB,i(2) 1 22LB↖−3, −10B(2) B(1) 00,1↗LB,i(1) 1 12LB↖−2, −10B(1) Fig4other spin particles are released by the fissions of zerospinparticles LB,f(3) ≡BL,3 ⊙−2, −1; −4, 1BR,3 −2, −1; −4, 1(25.1) LB,i(3) ≡BL,3 ⊙−2, 1; −4, −1BR,3 0, 1; −4, −1(25.2) LB,f(2) ≡BL,2 ⊙−1, −1; −3, 1BR,2 −1, −1; −3, 1(26.1) LB,i(2) ≡BL,2 ⊙−1, 1; −3, −1BR,2 −1, 1; −3, −1(26.2) LB,f(1) ≡BL,1 ⊙0,−1; −2, 1BR,1 0,−1; −2, 1(27.1) LB,i(1) ≡BL,1 ⊙0,1; −2, −1BR,1 0,1; −2, −1(27.2) LB−2 diag {...102,8 2,6 2,4 2,2 2, 02,2 2,4 2,6 2,8 2,10 2, ,...}(28)  4) Spin Interactions between Higgs Bosons and Gravitons d) To return to the case of scalar product of right-hand-to-right-hand particles, ARI AR,because we couldget no-trivial spin-coupling interactions between 0zero spin particle and 2spin particle. Here two groups of , Group-C and Group-D. are given. Analogously, illustration by example of the feature D(1) of Group-D as follows: Formulas (29.1) (29.2)and formulas (30.1), (30.2)are the third compoments of initial state iand final state fof scalar spin interaction of the first generation spin particles (l1) Initial state 030, 1diag {...6, 5, 4, 3, 2,1,0,-1, -2, -3, -4,...}(29.1) 23−3, 2diag {...5, 4, 3, 2, 1,0, -1, -2, -3, -4, -5,...}(29.2) Final state 1/2 30, 21 2diag {...13, 11, 9, 7, 5,3,1, -1, -3, -5,-7,...} (30.1) 3/2 3−3, 11 2diag {...9,7,5, 3, 1,-1, -3, -5, -7, -9, -11...} (30.2) And the conservation of the third compoment of spin angular momentums between initial state iand final state fis obtained as (31.0) 30, 1; −3, 230, 2; −3, 1(31.0) ininal sum of s.a.mfinal sum of s.a.m Where 30, 1; −3, 230, 13−3, 2(31.1) 30, 2; −3, 130, 23−3,1(31.2) And the conservation of scalar spin interaction about ininl state iand final statefis obtained as (32.0) LD,i(1) LD,f(1) LD(32.0) Where LD,i(1) DR,10,1; −3, 2I DR,1 0,1; −3, 2(32.1) LD,f(1) DR,10,2; −3, 1I DR,1 0,2; −3, 1(32.2) LD8I0(33) What mentionedabove is so-called fission of Higgs Boson and Graviton, refer to Fig8. Conservation (31.0) and conservation (32.0) imply that if initial state i and final state fexchange places, so-called fusion of other spinparticles is given, refer to Fig7. Fig5, Fig6 of Group-C are obtained by the analogy to those of Fig7, Fig8 of Group-D above.  C(3) 0−3,0 ↖LC,f(3) LC0↗−9, 62C(3) C(2) 0−2,0 ↖LC,f(2) LC↗−6, 42C(2) C(1) 0−1,0 ↖LC,f(1) LC↗−3, 22C(1) 0 0 fusions C C(3) 1−3, 6↗LC,i(3) LC↖−9,0 1C(3) C(2) 1−2, 4↗LC,i(2) LC↖−6,0 1C(2) C(1) 1−1,,2↗LC,i(1) LC↖−3,0 1C(1) Fig5HiggsBoson and Gravitonare formedby fusionsofother spin particles C(3) 1−3, 6↖LC,f(3) LC↗−9,0 1C(3) C(2) 1−2, 4↖LC,f(2) LC↗−6,0 1C(2) C(1) 1−1,,2↖LC,f(1) LC↗−3,0 1C(1) fissions C 0 0 C(3) 0−3,0 ↗LC,i(3) LC↖−9, 62C(3) C(2) 0−2,0 ↗LC,i(2) LC↖−6, 42C(2) C(1) 0−1,0 ↗LC,i(1) LC↖−3, 22C(1) Fig6other spin particlesare releasedby fissions of HiggsBoson and Graviton LC,f(3) ≡CR,3 ⊙−3, 6; −9,0 I0CR,3 −3, 6; −9,0 (34.1) LC,i(3) ≡CR,3 ⊙−3,0 ; −9, 6I0CR,3 −3,0 ; −9, 6(34.2) LC,f(2) ≡CR,2 ⊙−2, 4; −6,0 I0CR,2 −2, 4; −6,0 (35.1) LC,i(2) ≡CR,2 ⊙−2,0 ; −6, 4I0CR,2 −2,0 ; −6, 4(35.2) LC,f(1) ≡CR,1 ⊙−1, 2; −3,0 I0CR,1 −1, 2; −3,0 (36.1) LC,i(1) ≡CR,1 ⊙−1,0 ; −3, 2I0CR,1 −1,0 ; −3, 2(36.2) LC8I0(37)  D(3) 0−2, 1↖LD,f(3)LD↗−9, 62D(3) D(2) 0−1, 1↖LD,f(2) LD↗−6, 42D(2) D(1) 00,1↖LD,f(1) LD↗−3, 22D(1) 1 0 fusions D D(3) 5/6 −2, 6↗LD,i(3) LD↖−9, 17/6 D(3) D(2) 3/4 −1, 4↗LD,i(2) LD↖−6, 15/4 D(2) D(1) 1/2 0,2↗LD,i(1) LD↖−3, 13/2 D(1) Fig7Higgs Boson and Graviton are formedby fusions of other spin particles D(3) 5/6 −2, 6↖LD,f(3) LD↗−9, 17/6 D(3) D(2) 3/4 −1, 4↖LD,f(2) LD↗−6, 15/4 D(2) D(1) 1/20,2↖LD,f(1) LD↗−3, 13/2 D(1) fissions D 1 0 D(3) 0−2, 1↗LD,i(3) LD↖−9, 62D(3) D(2) 0−1, 1↗LD,i(2) LD↖−6, 42D(2) D(1) 00,1↗LD,i(1) LD↖−3, 22D(1) Fig8other spin particles are releasedby fissions of Higgs Boson and Graviton LD,f(3) ≡DR,3 ⊙−2, 6; −9, 1I0DR,3 −2, 6; −9, 1(38.1) LD,i(3) ≡DR,3 ⊙−2, 1; −9, 6I0DR,3 −2, 1; −9, 6(38.2) LD,f(2) ≡DR,2 ⊙−1, 4; −6, 1I0DR,2 −1, 4; −6, 1(39.1) LD,i(2) ≡DR,2 ⊙−1, 1; −6, 4I0DR,2 −1, 1; −6, 4(39.2) LD,f(1) ≡DR,1 ⊙0,2; −3, 1I0DR,1 0,2; −3, 1(40.1) LD,i(1) ≡DR,1 ⊙0,1; −3, 2I0DR,1 0,1; −3, 2(40.2) LD8I0(41)  5) Conclusions LA(l)andLB(l) in paragraph 3), which construct self-actions of zero spin particles, could be thought of as the Lagrangian function of Higgs Boson in quantum quantumfield.Further research could show that such kind of mechanismmaylead to the change ofsymmetry breakingin the StandardModel. LC(l)LD(l) in paragraph 4),which construct creation and annihilation between 0zero spin particlesand 2spin particle,may be able to dectect the existent of graviton from the ‘particulate’ nature of gravitation experimentally, comparative study, wavelike propertiesofgravitation havebeen exhibited [5] References [1]Higgs, Peter Broken Symmetries and the Masses of Gauge Bosons Physical Review Letters 13 (16) 508–509 Bibcode:1964 PhRvL..13..508H. doi:10.1103/PhysRevLett. 13.508 (1964) European particle physics laboratory, CERN, (2012) [2]ShaoXu Ren Advanced Non-Euclidean Quantum Mechanics ISBN 978-7-80703-585-4 (2006) The Third Kind of Particles ISBN 978-7-900500-91-5 (2011) ISBN 978-988-15598-9-0 (2012) ISBN 988-3-659-17892-4 (2012) The Third Kind of Particles Journal of Modern Physics, 5, 800-869 http:/dx.doi.org/10.4236/jmp.2014.59090 [3]ShaoXu Ren The Origins Of Spins Of Elementary Particles ISBN 978-988-13649-7-5 (2014) The Origins of Bosons and Fermions Journal of Modern Physics, 5, 1848-1879 http:/dx.doi.org/10.4236/jmp.2014.517181 [4]ShaoXu Ren Interaction of the Origins of Spin Angular Momentum ISBN 978-988-14902-0-9 (2016 2ndedition) [5]LIGO, LSC (2016) [6]ShaoXu Ren Faster Than Velocity Of Light (Infinite Dimensional Lorentz Group Of TKP )ISBN 978-988-12266-2-4 (2013)  6) Appendix: Higgs Boson Wave Differential Equation of First Order and Klein–Gordon Wave Differential Equation e) Usingmathelements j,kin STS[4], the Hamiltoniansof the first order and the second order linearwave differential equantions of 0spin zero particles, (Higgs Boson) are written as the following: Hj,jll{Hj,jll3m} (A–1) Hj,jl;k,kllHj,jllHk,kll(A–2) Hj,jllin (A–1) is kinectic energy. Thereare many combinations in (A–2),which made by various choise of jand k. For clarity, here l1 andomittingthemark " 1" in aboveexpressions. Then, taking jk−1 in casesof (A–1) and (A–2). getting below: For (A–1)H−1,0 1−1,0 P(A–3) and first order wave differential equantions of 0spin zero particle 0{i∂t−1−1,0 P−3m}−1,0 0 (A–4) For (A–2)H−1,0;−1,0 H−1,0 2m2(A–5) and second order wave differential equantions of 0spin zero particle 0{∂tt 2H−1,0 2m2}−1,0 0 (A–6) To make it clearer, we consinder the diagonal terms of (A–5) and have: diagonal {H−1,0 2} (A–7) diag{, –25/2, –16/2, –9/2, –4/2, –1/2,0,–1/2, –4/2, –9/2, –16/2,–25/2, }P1 2 diag{, –25/2, –16/2, –9/2, –4/2, –1/2,0,–1/2, –4/2, –9/2, –16/2,–25/2, }P2 2 diag{,25, 16,9, 4, 1,0, 1, 4, 9, 16,25,}P3 2 (A–8) {−1 2{P1 2P2 2}P3 2}0 20(A–9) 0 20diag{, 52,4 2,3 2,2 2,1 2, 02,1 2,2 2,3 2,4 2,5 2, } (A–10) (A–9) indicates {−1 2{P1 2P2 2}P3 2}⊂diagonal {H−1,0 2;0spin }(A–11) and{∂tt 21 2{∂xx 2∂yy 2}−∂ zz 2m2}diagonal; −1,0 0 (A–12)  f) The Hamiltonians of the first order and the second order linear differential equantions of /2 spin Fermion particles are written as following: Hj,j−2ll{Hj,j−2ll3m} (A–13) Hj,j−2l;k,k−2llHj,j−2llHk,k−2ll(A–14) Accordingly, taking jk0 in case of (A–13) and (A–14), we get: For (A–13)H0,−2210,−2P(A–15) and first order wave differential equantions of /2 spin particle /2{ i∂t−210,−2P−3m}0,−20 (A–16) For (A–14)H0,−2;0,−2H0,−2 2m2(A–17) and second order wave differential equantions of /2 spin particle /2{ ∂tt 2H0,−2 2m2}0,−20 (A–18) Taking out the diagonal terms from(A–17) and have: diagonal {H0,−2 2} (A–19) diag{,–39, –23, –11, –3,1,1, –3, –11, –23, –39, –59, }P1 2 diag{,–39, –23, –11, –3,1,1, –3, –11, –23, –39, –59, }P2 2 diag{,81, 49, 25, 9, 1,1, 9, 25, 49, 81,121,}P3 2 (A–20) Now, we see the two terms (A–21) in the center part of diagonal {H0,−2 2} (A–20),is just the square sumHDirac 2of kinectic energy of well-known Dirac equation of second order. {HDirac 2}diag{..., 1,1, ...}{P1 2P2 2P3 2}⊂diagonal {H0,−2 2} (A–21) Or{HDirac 2}{HKG}−∇2⊂diagonal {H0,−2 2;/2spin }(A–22) And contrast with (A–11), we get {HDirac 2}{HKG}−∇2diagonal {H−1,0 2;0spin }(A–23) Formula (A–22) and (A-23) mean:−∇2is a subset of H0,−2 2,not a set ofH −1,0 2.So Klein-Gordon Equation {2∂tt 2−c22∇2m2c4}KG 0 (A–24) {−2}KG 0 (A–25) ∇2−∂ tt 2/c2,mc/(A–26) is closer to /2 spin Fermion particle,rather than0spin Boson particle. It is more reasonable to use equation (A–4), equation (A–6) to describe zero spin Boson particle (Higgs Boson) than touse Klein Gordon equation.  g) For Vacuum Spin particle, VSP, –/2 negative one-second fermion particle, its Hamiltoniansof the first order and the second order linear wave differential equantions are written asthe following: Hj,jl{Hj,jl3m} (A–27) Hj,j;k,klHj,jlHk,kl(A–28) Taking jk0 in case of (A–27) and (A–28), we get: For (A–27)H0,0 210,0 P(A–29) and first order wave differential equantions of –/2 spin particle –/2{ i∂t−210,0 P−3m}0,0;VSP 0 (A–30) For (A–28)H0,0;0,0 H0,0 2m2(A–31) and second order wave differential equantions of –/2 spin particle –/2{ ∂tt 2H0,0 2m2}0,0;VSP 0 (A–32) Taking out the diagonal terms from(A–31) and have: diagonal {H0,0 2} (A–33) diag{, –61,–41, –25, –13, –5, –1, –1, –5, –13, –25, –41, }P1 2 diag{, –61,–41, –25, –13, –5, –1, –1, –5, –13, –25, –41, }P2 2 diag{,121,81, 49, 25, 9, 1,1, 9, 25, 49, 81,}P3 2 (A–34) Now turn to the two terms (A–35)in the center part of diagonal {H0,0 2} {HVSP }diag{..., 1,1, ...}{–P1 2−P2 2P3 2}⊂diagonal {H0,0 2} (A–35) and have wave equation of VSP, (–/2 spin fermion particle) {∂tt 2∂xx 2∂yy 2−∂ zz 2m2}VSP 0 (A–36) h) Next we shall discussthe solutions 0≡j,0 m0of zero mass particle differential equantions of First Order,which are based on free −/2 VSP particle (A–30),free 0zero spin particle (Higgs Boson) (A–4),free /2 Dirac spin particle (A–16).Which are given as below: −/2{ i∂t−20,0 P}0,0;VSP 00 (A–37) 0{i∂t−−1,0 P}−1,0;Higgs Boson 00 (A–38) /2{ i∂t−20,−2P}0,−2;Dirac 00 (A–39)  Notation: EE p,pp1 2p2 2p3 2(A–40) h1) For free −/2 VSP zero mass particle (A–37) 0,0;VSP 0F0,0 e−iEt (A–41) Getting Fp;0,0 e−iEtF−p;0,0 e−iE−t −p−p35/p 5 p−p34/p 4 −p−p33/p 3 p−p32/p 2 −p−p31/p 1 p−p30/p 0 pp30/p− 0 −pp31/p− 1 pp32/p− 2 −pp33/p− 3 pp34/p− 4 −pp35/p− 5 e−iEt pp35/p 5 pp34/p 4 pp33/p 3 pp32/p 2 pp31/p 1 pp30/p 0 p−p30/p− 0 p−p31/p− 1 p−p32/p− 2 p−p33/p− 3 p−p34/p− 4 p−p35/p− 5 e−iE−t (A–41.1) (A–41.2) Fp;0 −tan5/2 e−i5 tan4/2 e−i4 −tan3/2 e−i3 tan2/2 e−i2 −tan1/2 e−i ei0 F−p;0 cot5/2 e−i5 cot4/2 e−i4 cot3/2 e−i3 cot2/2 e−i2 cot1/2 e−i ei0 Fp;0 ei0 −cot1/2 ei cot2/2 ei2 −cot3/2 ei3 cot4/2 ei4 −cot5/2 ei5 F−p;0 ei0 tan1/2 ei tan2/2 ei2 tan3/2 ei3 tan4/2 ei4 tan5/2 ei5 (A–41.3) (A–41.4) VSP particleFp;0,0 Fp;0Fp;0(A–41.5) F−p;0,0 F−p;0F−p;0(A–41.6)  h2) For free 0zero spin zero mass particle (Higgs Boson) (A–38) −1,0;HB 0F−1,0 e−iEt (A–42) Getting p;−1,0;HB 0−p;−1,0;HB 0 −p−p34p/p 5 p−p33p/p 4 −p−p32p/p 3 p−p31p/p 2 −p−p30p/p 1 p∓p30p0/p 0 −pp30p/p− 1 pp31p/p− 2 −pp32p/p− 3 pp33p/p− 4 −pp34p/p− 5 e−iEt pp34p/p 5 pp33p/p 4 pp32p/p 3 pp31p/p 2 pp30p/p 1 pp30p0/p 0 p−p30p/p− 1 p−p31p/p− 2 p−p32p/p− 3 p−p33p/p− 4 p−p34p/p− 5 e−iE−t (A–42.1) (A–42.2) −tan4/2 e−i5 tan3/2 e−i4 −tan2/2 e−i3 tan1/2 e−i2 −e−i sin −ei cot 1/2 ei2 −cot 2/2 ei3 cot 3/2 ei4 −cot 4/2 ei5 e−iEt cot4/2 e−i5 cot3/2 e−i4 cot2/2 e−i3 cot1/2 e−i2 e−i sin ei tan 1/2 ei2 tan 2/2 ei3 tan 3/2 ei4 tan 4/2 ei5 e−iE−t (A–42.3) (A–42.4) There are two singularities at 0, andin the above two expressions.Obviously, some uncertainties of choise of free 0zero spin zero mass wavefunction should be addressed. Here(A–42.3) and (A–42.4) are only an investigation.  h3) For free /2 Dirac spin zero mass particle (A–39) 0,−2;Dirac 0F0,−2e−iEt (A–43) Getting p;0,−2;Dirac 0−p;0,−2;Dirac 0 ...... pp34/p 4 pp33/p 3 pp32/p 2 pp31/p 1 pp30/p 0 p−p31/p− 1 p−p32/p− 2 p−p33/p− 3 p−p34/p− 4 p−p35/p− 5 ..... e−iEt, ...... −p−p35/p 5 p−p34/p 4 −p−p33/p 3 p−p32/p 2 −p−p31/p 1 p∓p30/p 0 −pp31/p− 1 pp32/p− 2 −pp33/p− 3 pp34/p− 4 ...... e−iE−t (A–43.1) (A–43.2) ...... cot4/2cos /2e−i4 cot3/2cos /2 e−i3 cot2/2cos /2 e−i2 cot1/2cos /2 e−i cos /2 sin /2 ei tan1/2sin /2 ei2 tan2/2sin /2 ei3 tan3/2sin /2 ei4 tan4/2sin /2 ei5 ..... e−iEt, ...... −tan4/2sin /2 e−i5 tan3/2sin /2 e−i4 −tan2/2sin /2 e−i3 tan1/2sin /2 e−i2 −sin /2 e−i cos /2 −cot1/2cos /2 ei cot2/2cos /2 ei2 −cot3/2cos /2 ei3 cot4/2cos /2 ei4 ..... e−iE−t (A–43.3) (A–43.4) The two elements in the centersof the above expressions are just the spin wavefunction representation of operatornof /2Diracspinintwo dimensional spin space intraditional quantum machenics. p;Dirac 0−p;Dirac 0 cos /2 sin /2 ei,−sin /2e−i cos /2 (A–43.5) (A–43.6)  i) Finally we digress slightly, to tackle the situations of the velocity of light,because light speed is related to spin angular momentum in STS. i1) The special case of P1P10 for non-zeromass particle Second Order differential equantions –/2 (A-32), VSP particle, zerospin particle (Higgs Boson) (A-6), /2 Dirac spin particle (A–18) are givenbelow: −/2{ E20,0 2∂zz 2−m2}0,0;VSP 0 (A–44) 0,0 2diag{,121,81, 49, 25, 9, 1,1, 9, 25, 49, 81,} 0{E2−1,0 2∂zz 2−m2}−1,0;Higgs Boson0 (A–45) −1,0 2diag{, 25,16,9,4,1,0, 1, 4,9, 16, 25,} /2{ E20,−2 2∂zz 2−m2}0,−2;Dirac 0 (A–46) 0,−2 2diag{,81, 49, 25,9, 1,1, 9,25, 49, 81,121,} getting [2] ES|j−k| m2c4i,j 2c2P3 2≥m2c4c2P3 2(A–47) Photon velocity in multi-level universes world is quantized:the limiting speed of particle with zero massm0,could be greaterthan c CS|j−k|i,jc1c,2c,3c,4c,...or 1c,3c,5c,7c,...≥c, (A–48) i2) Lorentz Group Operators are constructed by six44 dimensional matrices : J1,J2,J3and K1,K2,K3 J1 0000 0000 000−i 00i0 ,J2 0000 000i 0000 0−i00 ,J3 00 0 0 00−i0 0i00 00 0 0 (A–49) K1 0i00 i000 0000 0000 ,K2 00i0 0000 i000 0000 ,K3 000i 0000 0000 i000 (A–50) K3i∂ ∂3L3|30i∂ ∂3 Ch 00Sh 0100 0010 Sh 00Ch |30(A–51) L3is the familiar expressionof Einstein special relativity.  Using infinite dimensional spin augular momentum operators−2,1 (1: −2,1 ,2: −2,1 ,3: −2,1 )of1spin boson particle, we could get six infinite dimensional matricesJ1,J2,J3and K1,K2,K3of Lorentz Group Operators. Among them,matrix K3is shown below K3K3 0000 5i 0000 4i 0000 3i 0000 2i 000i 0000 0000 i000 2i0000 3i0000 4i0000 5i0000 (A–52) Or K3K3 0000 5 00004 00003 00002 0001 0000 0000 −1000 −2 0000 −3 0000 −4 0000 −5 0000 (A–53) Take note of (A–52) and (A–53),they are two different types of Non-Hermitian operators, antisymmetrical matrices,base on them,proceed as follows L3L3(A–54)  From (A–57), some curious spectacles that similar to (A–48) are emerged [6] : For (A–52),For (A–53) L3 00Ch Sh Sh Ch ,L3 00Sech −Th Th Sech L3 01Ch 2Sh 2 Sh 2Ch 2,L3 01Sech 2−Th 2 Th 2Sech 2 L3 02Ch 3Sh 3 Sh 3Ch 3,L3 02Sech 3−Th 3 Th 3Sech 3 ..... ..................... ................ (A–55) (A–56) Then, Einstein Special Relativity is extended to the following so-called: Worm Hole Special Relativity in Multi-Level Universes World:[6] x0, j ′ x3, j ′L3 0, jx0, j x3, j(A–57) For (A–55), have:,For (A–56), have x0 ′Ch x0Sh x3,x0 ′Sechx0−Th x3 x3 ′Sh x0Ch x3,x3 ′Th x0Sech x3 ,2,3,... ,,2,3,... (A–58) (A–59) and Sh (A–58.1), Th (A–59.1) Ch (A–58.2), Sech (A–59.2) Th (A–58.3), Sh (A–59.3) Ch2−Sh21 (A–58.4),Sech2Th21 (A–59.4) j) Spin Topological Space STS is the space that could discribe and help people understand how the transitions of particle spins, between various types of spin particles,are happening.Before this,the concepts of physicsand math about these transitions were indistinct andblurred. To appreciate the beauty and subtlety of STS, theFIG.below is essential. 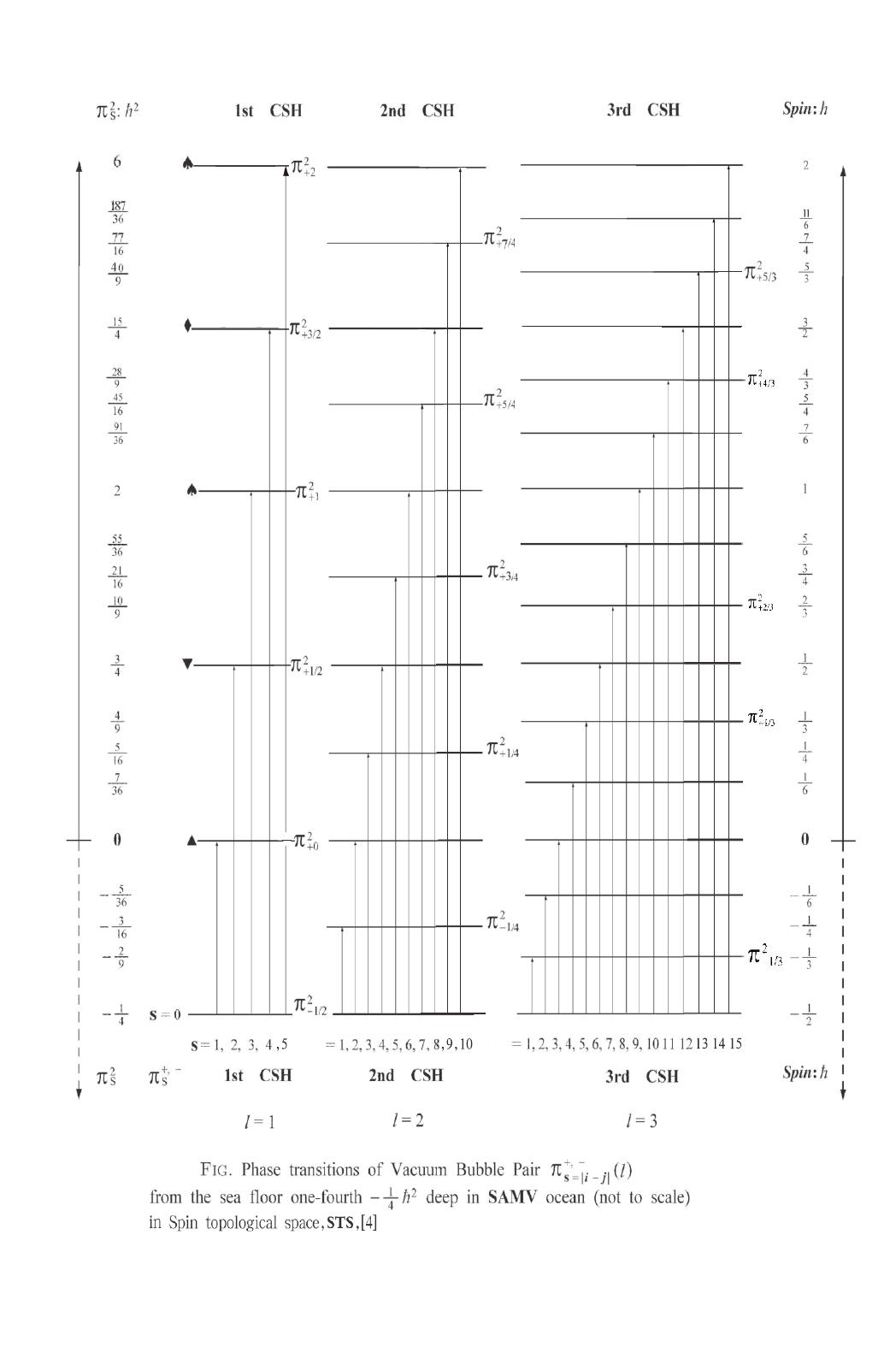 |

