 Vol.3, No.7, 622-632 (2011) Natural Science http://dx.doi.org/10.4236/ns.2011.37085 Copyright © 2011 SciRes. OPEN ACCESS Closed virial equations for hard parallel cubes and squares Leslie V. Woodcock Instituto Ciệnce Exacte, Departamento de Fisica, Universidade Federal de Juiz de Fora, Juiz de Fora, Brazil; *Corresponding Author: les.woodcock@manchester.ac.uk Received 20 May, 2011; revised 15 June, 2011; accepted 23 June, 2011. ABSTRACT A correlation between maxima in virial coeffi- cients (Bn), and “kissing” numbers for hard hy- per-spheres up to dimension D = 5, indicates a virial equation and close-packing relationship. Known virial coefficients up to B7, both for hard parallel cubes and squares, indicate that the limiting differences Bn – B(n-1) behave similar to spheres and disks, in the respective expansions relative to maximum close packing. In all cases, the difference Bn – B(n-1) is approaching a nega- tive constant with similar functional form in each dimension. This observation enables closed-virial equations-of-state for cubes and squares to be obtained. In both the 3D and 2D cases, the virial pressures begin to deviate from MD thermodynamic pressures at densities well below crystallization. These results consolidate the general conclusion, from previous papers on spheres and disks, that the Mayer cluster expansion cannot represent the thermodynamic fluid phases up to freezing as commonly as- sumed in statistical theories. Keyw ords: Virial Equations Liquid Theory 1. INTRODUCTION An equation-of-state for the hard-sphere fluid pressure (p) was obtained by analytical closure of the virial ex- pansion in powers of density relative to close-packing [1]. The virial series is simply a Maclaurin expansion of the pressure as a state function about zero density, and can be written in dimensionless form 1 10 1B n n n Z (1) where Z = pV/NkBT, T is absolute temperature, kB is Boltzmann’s constant, Bn are the dimensionless coeffi- cients is the number density NV , and 0 is the crystal close packing density. The theory of the coef- ficients Bn is well-established; exact statistical expres- sions for Bn are available as the cluster integrals that are calculated analytically up to B4 and presently available numerically up to B10. A closed form of Eq.1 based only upon known coeffi- cients, B1 to B10, has been shown to be everywhere con- vergent up to its first pole at 0 . The equation-of-state is accurate for the equilibrium hard-sphere fluid, yield- ing the same thermodynamic pressures as may now be obtained with 6-figure precision from MD simulations of up-to a million spheres [2]. A more refined scrutiny of the margins of difference, with due consideration of the uncertainties, however, shows that the virial equation begins to deviate from the thermodynamic pressure equation, albeit very slightly, at a density in the mid- fluid range close to the available volume percolation transition [3]. It has also been shown that the known virial series of the two-dimensional (D = 2) hard-disk fluid is also amenable to closure [4]; an equation-of-state is obtained with 6-figure accuracy at low density. As in the D = 3 case, but more pronounced however, there is a clearer deviation well-below the freezing transition. A subse- quent more accurate analytical closed form for the pres- sure equation-of-state for hard disks was derived [5]. The precision of this revised version of the closed virial equation was such that we were able to conclude that the deviation from the thermodynamic pressure occurs at or near the 2D-percolation density of available, or excluded volume, 2 pa 04. , determined previously by Hoover et al. [6]. Thus, for both disks (D = 2) and spheres (D = 3) the virial equations-of-state do not represent the thermodynamic state functions for densities above the respective free volume percolation transitions. It is also worth noting that the known virial coeffi- cients for D = 4 hyper-spheres [7], in powers of density relative to close packing, also increase from B1 – B6, then decrease with Bn – B(n-1) linearly with n, going negative at n = 10. This indicates that the higher virial coefficients should eventually go negative, yielding a  L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 623 closed virial equation with a negative pressure pole at maximum packing in this case also. These empirical observations regarding the destiny of the virial equations-of-state at higher densities would appear to confirm that the percolation transitions in these hard-core model fluids may indeed be higher-order thermodynamic phase transitions that signify the onset of the divergence of the virial pressure equation from the thermodynamic pressure. There are those who seem to “religiously” believe the Mayer virial series is equivalent to the thermodynamic fluid equation-of-state; this is a common misapprehension amongst physicists. The suggestion that the virial expansion may not rep- resent the physical thermodynamic state for densities above the percolation transition is not new. For both hard parallel cubes and hard parallel squares, the virial coeffi- cients are known up to B7 [8-10] In fact, it has been known for 50 years that the virial coefficients for parallel cubes go negative [10]. MD calculations 25 years ago [11], of the thermodynamic and transport properties of hard parallel cubes, indicated that the hard-parallel-cube fluid virial equation deviates above the percolation tran- sition, at a density well-below the freezing transition. Kratky [12] further elucidated upon the suggestion the percolation transitions in spheres and disks may be higher order thermodynamic phase transitions. Refer- ence [12] also gives valuable definitions and discussion of the various percolation transitions in hard-core fluids generally. On revisiting the known virial coefficients for both fluid systems of parallel cubes and squares (Table 1), it can be seen that in both cases, now in the expansion of the packing fraction (y = /0 ) even from just the known coefficients up to B7, the differences Bn – B(n-1) are approaching negative constants with functional forms analogous to the D = 3 spheres [1-3] and D = 2 disks [4,5] cases respectively. Here we obtain and test the closed virial equations-of-state for the systems of parallel cubes and squares, which by analogy with the closed equations of spheres [1-3] and disks [4,5], and then compare with available MD data from the literature. 2. “KISSING” NUMBERS AND VIRIAL COEFFICIENTS The first simple observation we make, about the Bn values in Table 1, is that for both D = 3 and D = 2, Bn first increases with n, peaks at n = 4 (3D) or 5 (2D) and then begin to decrease, and in the case of the cubes go negative. This is just the same behavior that is seen gen- erally in hyper-spheres of D > 1, i.e. D = 2, 3, 4 and 5. The highest virial coefficient in all these cases is of the same order as a maximum co-ordination or contact numbers, known as “kissing numbers” to mathemati Table 1. Known virial coefficients of the parallel hard-cube fluid (D = 3) and parallel hard square fluid (D = 2): also given in columns 3 and 5, for D = 3 and 2 respectively, are the pre- dicted values up to B12 from the closed virial equations ob- tained here. n Bn [D = 3] Eq.3 Bn [D = 2] Eq.6 1 1 1 2 4 2 3 9 3 4 11.33333 3.666666 5 3.16 3.7222 6 –18.88 –18.88 3.025 3.0407 7 –43.5 –43.50 1.65 1.6714 8 –69.00 –0.3857 9 –94.50 –3.1306 10 –120.00 –6.5633 11 –145.50 –10.6838 12 –171.00 –15.4921 cians [12], of contiguous spheres to a central sphere. This correlation provides salient evidence that the virial expansions about zero density, in powers of density rela- tive to close packing, Eq.1, reflects information about the close packed state, and is per se suggestive of the closed forms with the first poles at that maximum den- sity. The kissing number is simply defined as the maxi- mum number of hyper-spheres in a configuration of like spheres that may be contiguous with a central sphere at the same time. This number is not necessarily the lattice near-neighbor number, but for the lower dimensions up to D = 5, it can represent the first co-ordination number in the most stable crystal structure at infinite pressure, or equivalently, at zero temperature. Kissing numbers for hyper-spheres are known up to D = 28 [12] but here (Figure 1) we compare with D = 1 to D = 5. The corre- lation is convincing evidence that the virial expansion of non-space-filling hyper-spheres does not reflect the physically unreal packing (y = 1), seen in many theo- retical approximate virial equations, but rather the maximum crystal close-packed states (0 ). Looking again at Table 1, the Bn values for the cases D = 3 (cubes) and D = 2 (squares) have similar maxima at B4 (D = 3) value 11.3333 and B5 (D = 2) value 3.7222. There are three different types of “kisses” in these sys- tems, faces, edges and corners. Counting only faces and edges, we get for Bmax + D, 14.3 and 5.7, compared to 14 and 4 for the respective kissing numbers of cubes and squares respectively. In these cases, the density relative to close packing 0 = packing fraction y, and the maximum density corresponds to y = 1. 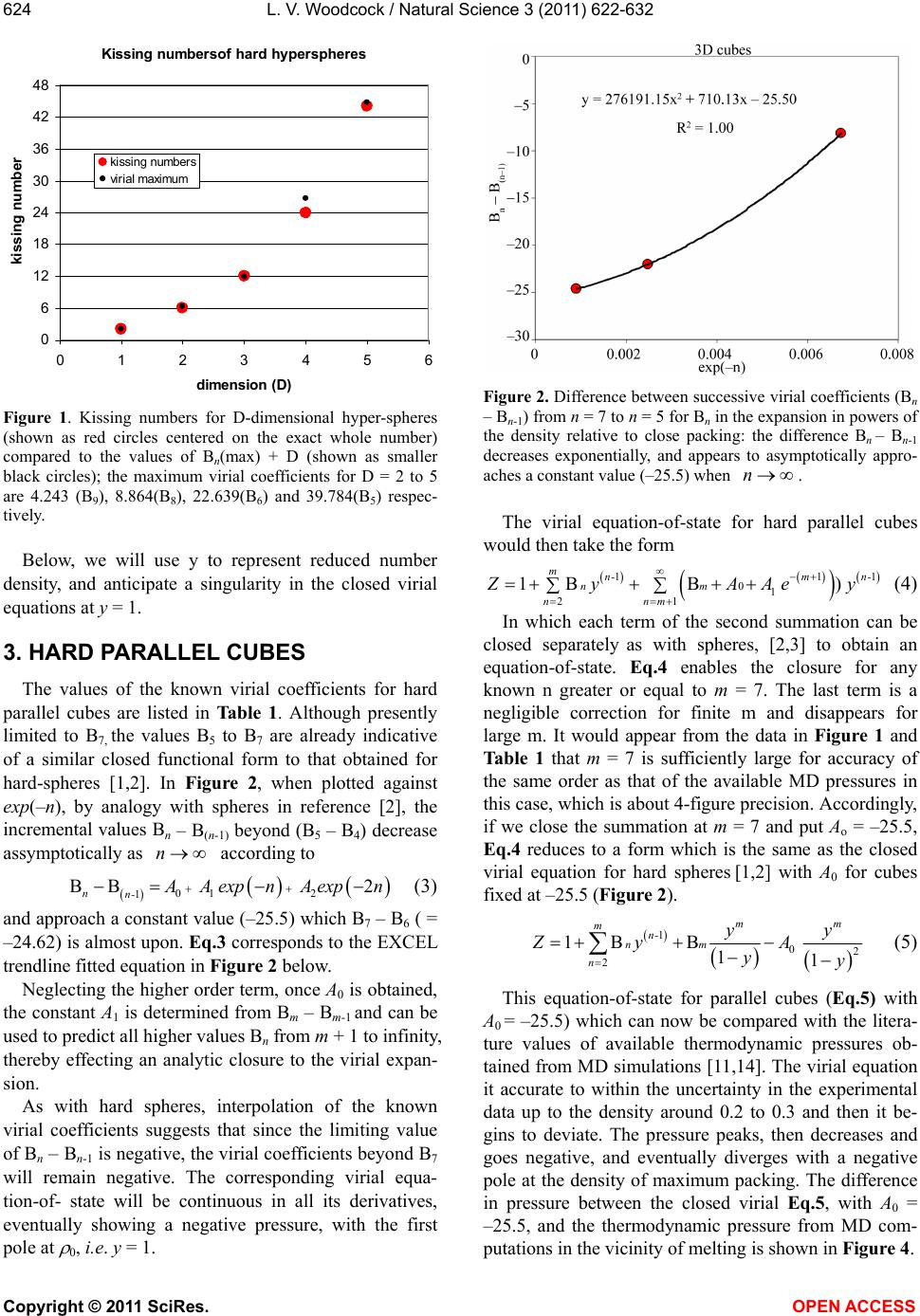 L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 624 Kissing numbersof hard hyperspheres 0 6 12 18 24 30 36 42 48 0123456 dimension (D) kissing numbe kissing numbers virial maximum Figure 1. Kissing numbers for D-dimensional hyper-spheres (shown as red circles centered on the exact whole number) compared to the values of Bn(max) + D (shown as smaller black circles); the maximum virial coefficients for D = 2 to 5 are 4.243 (B9), 8.864(B8), 22.639(B6) and 39.784(B5) respec- tively. Below, we will use y to represent reduced number density, and anticipate a singularity in the closed virial equations at y = 1. 3. HARD PARALLEL CUBES The values of the known virial coefficients for hard parallel cubes are listed in Table 1. Although presently limited to B7, the values B5 to B7 are already indicative of a similar closed functional form to that obtained for hard-spheres [1,2]. In Figure 2, when plotted against exp(–n), by analogy with spheres in reference [2], the incremental values Bn – B(n-1) beyond (B5 – B4) decrease assymptotically as n according to 01 2 1 BB 2 nn- A A expn A expn (3) and approach a constant value (–25.5) which B7 – B6 ( = –24.62) is almost upon. Eq.3 corresponds to the EXCEL trendline fitted equation in Figure 2 below. Neglecting the higher order term, once A0 is obtained, the constant A1 is determined from Bm – Bm-1 and can be used to predict all higher values Bn from m + 1 to infinity, thereby effecting an analytic closure to the virial expan- sion. As with hard spheres, interpolation of the known virial coefficients suggests that since the limiting value of Bn – Bn-1 is negative, the virial coefficients beyond B7 will remain negative. The corresponding virial equa- tion-of- state will be continuous in all its derivatives, eventually showing a negative pressure, with the first pole at 0, i.e. y = 1. Figure 2. Difference between successive virial coefficients (Bn – Bn-1) from n = 7 to n = 5 for Bn in the expansion in powers of the density relative to close packing: the difference Bn – Bn-1 decreases exponentially, and appears to asymptotically appro- aches a constant value (–25.5) when n. The virial equation-of-state for hard parallel cubes would then take the form 111 01 21 1B B) mn-m n- nm nnm yAA e y (4) In which each term of the second summation can be closed separately as with spheres, [2,3] to obtain an equation-of-state. Eq.4 enables the closure for any known n greater or equal to m = 7. The last term is a negligible correction for finite m and disappears for large m. It would appear from the data in Figure 1 and Table 1 that m = 7 is sufficiently large for accuracy of the same order as that of the available MD pressures in this case, which is about 4-figure precision. Accordingly, if we close the summation at m = 7 and put Ao = –25.5, Eq.4 reduces to a form which is the same as the closed virial equation for hard spheres [1,2] with A0 for cubes fixed at –25.5 (Figure 2). 1 02 2 1B B 11 mm mn- nm n yy yA yy (5) This equation-of-state for parallel cubes (Eq.5) with A0 = –25.5) which can now be compared with the litera- ture values of available thermodynamic pressures ob- tained from MD simulations [11,14]. The virial equation it accurate to within the uncertainty in the experimental data up to the density around 0.2 to 0.3 and then it be- gins to deviate. The pressure peaks, then decreases and goes negative, and eventually diverges with a negative pole at the density of maximum packing. The difference in pressure between the closed virial Eq.5, with A0 = –25.5, and the thermodynamic pressure from MD com- putations in the vicinity of melting is shown in Figure 4. 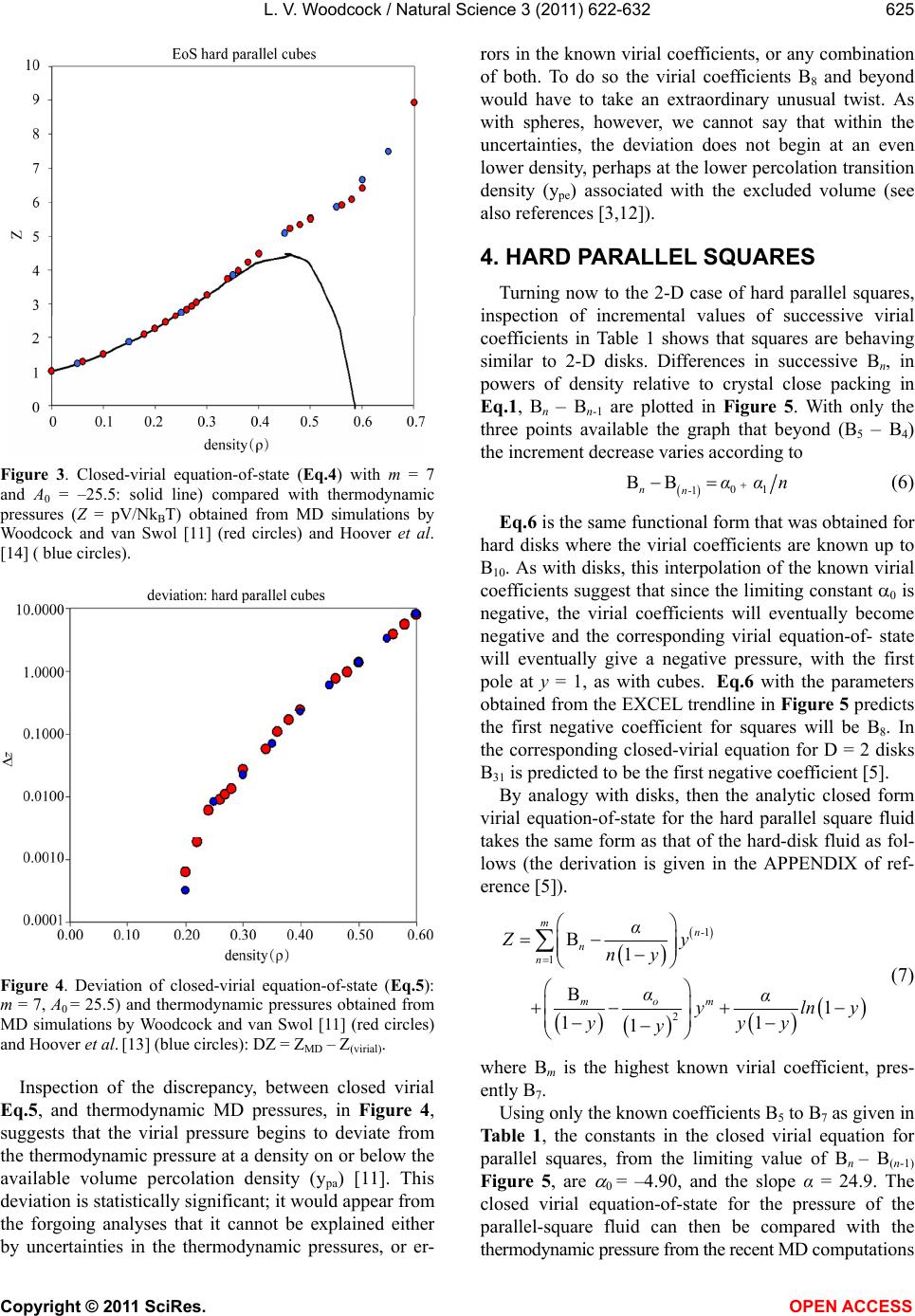 L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 625 Figure 3. Closed-virial equation-of-state (Eq.4) with m = 7 and A0 = –25.5: solid line) compared with thermodynamic pressures (Z = pV/NkBT) obtained from MD simulations by Woodcock and van Swol [11] (red circles) and Hoover et al. [14] ( blue circles). Figure 4. Deviation of closed-virial equation-of-state (Eq.5): m = 7, A0 = 25.5) and thermodynamic pressures obtained from MD simulations by Woodcock and van Swol [11] (red circles) and Hoover et al. [13] (blue circles): DZ = ZMD – Z(virial). Inspection of the discrepancy, between closed virial Eq.5, and thermodynamic MD pressures, in Figure 4, suggests that the virial pressure begins to deviate from the thermodynamic pressure at a density on or below the available volume percolation density (ypa) [11]. This deviation is statistically significant; it would appear from the forgoing analyses that it cannot be explained either by uncertainties in the thermodynamic pressures, or er- rors in the known virial coefficients, or any combination of both. To do so the virial coefficients B8 and beyond would have to take an extraordinary unusual twist. As with spheres, however, we cannot say that within the uncertainties, the deviation does not begin at an even lower density, perhaps at the lower percolation transition density (ype) associated with the excluded volume (see also references [3,12]). 4. HARD PARALLEL SQUARES Turning now to the 2-D case of hard parallel squares, inspection of incremental values of successive virial coefficients in Table 1 shows that squares are behaving similar to 2-D disks. Differences in successive Bn, in powers of density relative to crystal close packing in Eq.1, Bn – Bn-1 are plotted in Figure 5. With only the three points available the graph that beyond (B5 – B4) the increment decrease varies according to 01 1 BB nn- α αn (6) Eq.6 is the same functional form that was obtained for hard disks where the virial coefficients are known up to B10. As with disks, this interpolation of the known virial coefficients suggest that since the limiting constant 0 is negative, the virial coefficients will eventually become negative and the corresponding virial equation-of- state will eventually give a negative pressure, with the first pole at y = 1, as with cubes. Eq.6 with the parameters obtained from the EXCEL trendline in Figure 5 predicts the first negative coefficient for squares will be B8. In the corresponding closed-virial equation for D = 2 disks B31 is predicted to be the first negative coefficient [5]. By analogy with disks, then the analytic closed form virial equation-of-state for the hard parallel square fluid takes the same form as that of the hard-disk fluid as fol- lows (the derivation is given in the APPENDIX of ref- erence [5]). 1 1 2 B1 B1 11 1 mn- n n m mo α Zy ny αα ylny yyy y (7) where Bm is the highest known virial coefficient, pres- ently B7. Using only the known coefficients B5 to B7 as given in Table 1, the constants in the closed virial equation for parallel squares, from the limiting value of Bn – B(n-1) Figure 5, are 0 = –4.90, and the slope α = 24.9. The closed virial equation-of-state for the pressure of the parallel-square fluid can then be compared with the thermodynamic pressure from the recent MD computations 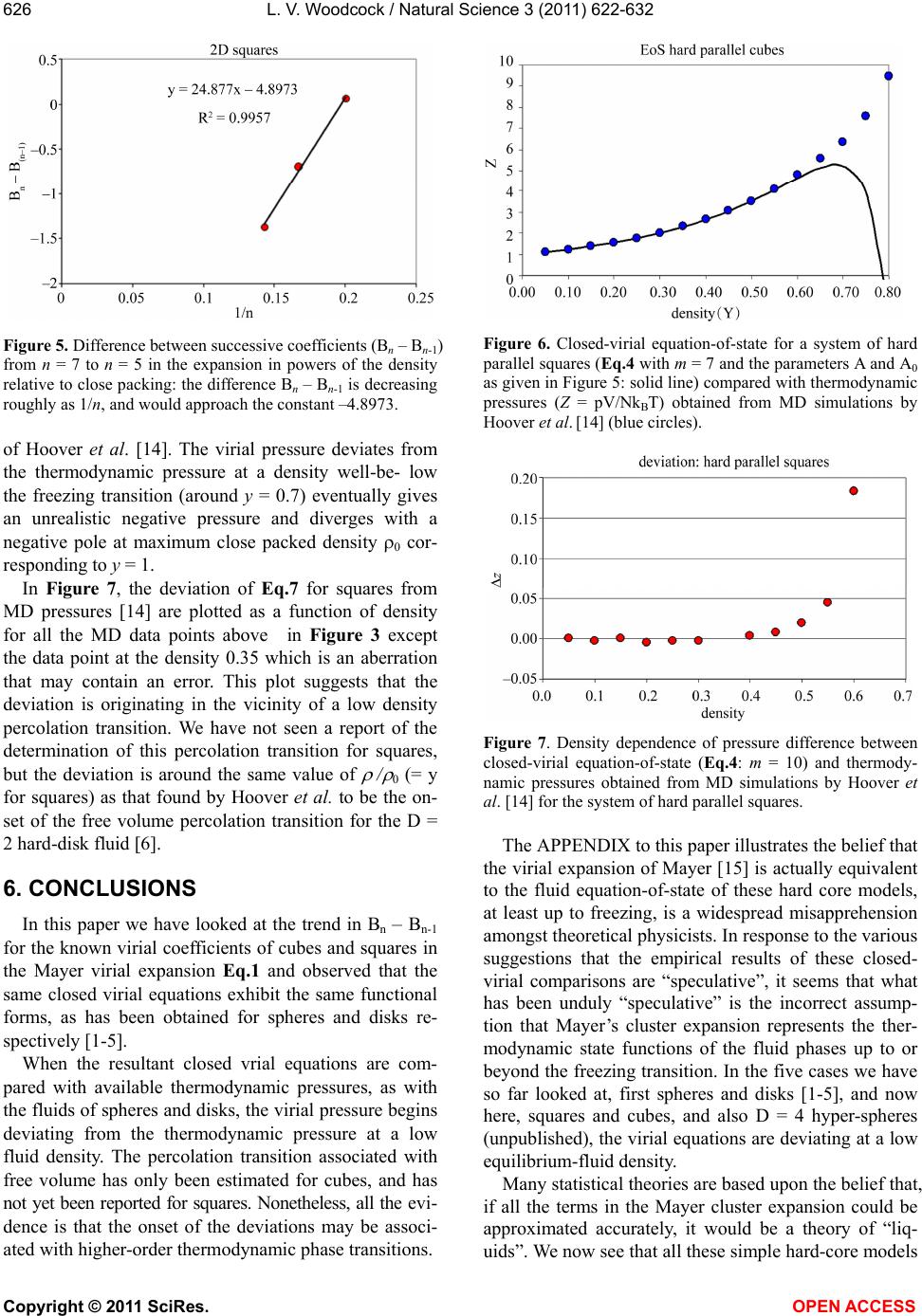 L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 626 Figure 5. Difference between successive coefficients (Bn – Bn-1) from n = 7 to n = 5 in the expansion in powers of the density relative to close packing: the difference Bn – Bn-1 is decreasing roughly as 1/n, and would approach the constant –4.8973. of Hoover et al. [14]. The virial pressure deviates from the thermodynamic pressure at a density well-be- low the freezing transition (around y = 0.7) eventually gives an unrealistic negative pressure and diverges with a negative pole at maximum close packed density 0 cor- responding to y = 1. In Figure 7, the deviation of Eq.7 for squares from MD pressures [14] are plotted as a function of density for all the MD data points above in Figure 3 except the data point at the density 0.35 which is an aberration that may contain an error. This plot suggests that the deviation is originating in the vicinity of a low density percolation transition. We have not seen a report of the determination of this percolation transition for squares, but the deviation is around the same value of / 0 (= y for squares) as that found by Hoover et al. to be the on- set of the free volume percolation transition for the D = 2 hard-disk fluid [6]. 6. CONCLUSIONS In this paper we have looked at the trend in Bn – Bn-1 for the known virial coefficients of cubes and squares in the Mayer virial expansion Eq.1 and observed that the same closed virial equations exhibit the same functional forms, as has been obtained for spheres and disks re- spectively [1-5]. When the resultant closed vrial equations are com- pared with available thermodynamic pressures, as with the fluids of spheres and disks, the virial pressure begins deviating from the thermodynamic pressure at a low fluid density. The percolation transition associated with free volume has only been estimated for cubes, and has not yet been reported for squares. Nonetheless, all the evi- dence is that the onset of the deviations may be associ- ated with higher-order thermodynamic phase transitions. Figure 6. Closed-virial equation-of-state for a system of hard parallel squares (Eq.4 with m = 7 and the parameters A and A0 as given in Figure 5: solid line) compared with thermodynamic pressures (Z = pV/NkBT) obtained from MD simulations by Hoover et al. [14] (blue circles). Figure 7. Density dependence of pressure difference between closed-virial equation-of-state (Eq.4: m = 10) and thermody- namic pressures obtained from MD simulations by Hoover et al. [14] for the system of hard parallel squares. The APPENDIX to this paper illustrates the belief that the virial expansion of Mayer [15] is actually equivalent to the fluid equation-of-state of these hard core models, at least up to freezing, is a widespread misapprehension amongst theoretical physicists. In response to the various suggestions that the empirical results of these closed- virial comparisons are “speculative”, it seems that what has been unduly “speculative” is the incorrect assump- tion that Mayer’s cluster expansion represents the ther- modynamic state functions of the fluid phases up to or beyond the freezing transition. In the five cases we have so far looked at, first spheres and disks [1-5], and now here, squares and cubes, and also D = 4 hyper-spheres (unpublished), the virial equations are deviating at a low equilibrium-fluid density. Many statistical theories are based upon the belief that, if all the terms in the Mayer cluster expansion could be approximated accurately, it would be a theory of “liq- uids”. We now see that all these simple hard-core models  L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 627 have two fluid phases, the low density gas phase where the Mayer virial expansion represents the thermody- namic state functions, and the high density fluid phase where it is invalid. Looking again at the theory of simple liquids, we may now conjecture that the high density fluid phase belongs to the same phase as the supercooled “liquid” phase, by definition. For hard-spheres this is the metastable branch that is a continuous extrapolation of the equilibrium high-density fluid at freezing, and which terminates at the random close packed (RCP) state. Perhaps we should now take another look at the RCP state as a starting point for the general theory of liquids. Standard treatises on simple liquids’ deal largely with theories of the liquid state based upon “configurational surgery” of Mayer virial cluster diagrams [15,16]. We now see that the Mayer cluster expansion whilst being an essentially exact theory of low density gases, may not be a starting point for theories of the liquid state. An analytical theory with all the virial coefficients correct would not still represent the high density equilibrium fluid. The title of Hansen and McDonald [16], when the 4th Edition comes to be published, might be retitled “The Theory of Simple Gases”! 5. ACKNOWLEDGEMENTS I wish to thank the Department of Physics at the Federal University of Juiz de Fora for a temporary visiting facility, and my host Professors, Socrates Dantas and Bernhard Lesche, for their support and kind hos- pitality. REFERENCES [1] Woodcock, L.V. (2008) Virial equation-of-state for hard spheres. ArXiv condensed matter. http://arxiv.org/abs/0801.4846 [2] Bannerman M., Lue, L. and Woodcock, L.V. (2010) Thermodynamic pressures for hard spheres and closed virial equation-of-state. Journal of Chemical Physics, 132, 084507-084513. [3] Woodcock, L.V. (2011) Percolation transitions in the hard-sphere fluid. AICHE Journal (accepted and pub- lished online). doi:10.1002/aic.12666 [4] Woodcock, L.V. (2008) Virial equation-of-state for the hard disk fluid. ArXiv condensed matter. [5] Beris, A. and Woodcock, L.V. (2010) Closed virial equa- tion-of- state for the hard-disk fluid. ArXiv condensed matter. [6] Hoover, W.G., Hoover, N.E. and Hanson, Exact, K. (1979) hard-disk free volumes. Journal of Chemical Physics, 70, 1837-1844. [7] Clisby, N. and McCoy, B.N. (2006) Ninth and tenth virial coefficients for hard hyper-spheres in D-dimensions. Physics and Astronomy, 122, 15-57. doi:10.1007/s10955-005-8080-0 [8] Zwanzig, R.W. (1956) Virial coefficients of parallel square and parallel cube gases. Journal of Chemical Physics, 24, 855-856. doi:10.1063/1.1742621 [9] Hoover, W.G. and De Rocco, A.G. (1961) Sixth virial coefficients for gases of parallel hard lines, squares, and cubes. Journal of Chemical Physics, 34, 1059-1060. doi:10.1063/1.1731634 [10] Hoover, W.G. and De Rocco, A.G. (1962) Sixth and sev- enth virial coefficients for the parallel hard cube model. Journal of Chemical Physics, 36, 3141-3162. doi:10.1063/1.1732443 [11] van Swol, F. and Woodcock, L.V. (1987) Percolation transition in the parallel hard cube model fluid, Molecu- lar Simulation, 1, 95-108. doi:10.1080/08927028708080934 [12] Kratky, K.W. (1988) Is the percolation transition of hard spheres a thermodynamic phase transition? Journal of Statistical Physics, 52, 1413-1421. doi:10.1007/BF01011656 [13] Geometry: Multidimensional Geometry: n-Dimensional Geometry http://mathworld.wolfram.com/KissingNumber.html [14] Hoover, W.G., Hoover, C. and Bannerman, M. (2009) Single speed molecular dynamics of hard parallel squares and cubes. Journal of Statistical Physics, 136, 715-732. doi:10.1007/s10955-009-9795-0 [15] Mayer, J.E. and Mayer, M.G. (1940) Statistical Mechan- ics John Wiley, New York. [16] Hansen, J.-P. and McDonald, I.R. (2006) The Theory of Simple Liquids, 3rd Edition, Academic Press, Oxford.  L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 628 APPENDIX 1. Debate on the Scientific Merit of Reference [5]: PRL anonymous Referee A said: “This manuscript appears to me to be seriously flawed and either the flaws must be corrected or it must be explained why my per- ceived objections are invalid. My concerns are as fol- lows: 1) It is rigorously established that the pressure is a monotonic non decreasing function of the density. Therefore it disturbing that the equation-of-state (4) di- verges to negative infinity as 0 rr. 2) The authors will argue that their equation (4) is called a “closed-virial equation-of-state'' to which the mono-tonicity argument does not apply. This argument itself is questionable and is in contradiction with every approximate equation of state of which I am aware. If the authors must persist in such a claim they must cite the many papers which they are contradicting and ex- plain why they are correct and the rest of the field is wrong. 3) The statement on page 5 that “the virial equation is continuous in all its derivatives'' makes no sense. In par- ticular if the system has a second or higher phase transi- tion as the authors suggest then the virial expansion will have a singularity (at which some derivative will diverge) at the phase transition density; a density which will be smaller than close packing. 4) On the purely numerical side of extrapolating virial coefficients beyond the first 10 which have been com- puted is it a completely unverified assumption that reli- able extrapolations may be carried out to order 31 which is where the authors claim that first negative coefficient occurs. 5) The authors seem to be completely unaware of the long debated and studied question of the nature of the transition in hard discs. At least they make no mention of this literature in their bibliography. The authors may find some of the references in their reference 4 relevant.” Objection 1) is based upon a misapprehension. The thermodynamic pressure of the hard-sphere fluid as de- fined and derived from a partition function, and obtained by MD simulations, is not necessarily the same as pres- sure of a purely theoretical low-density-limit virial ex- pansion. We do not know where the first phase transition is in the thermodynamic equation-of-state of the hard-disk fluid, but it must coincide with the initial de- viation of the virial equation, beyond which the virial equation must become physically unreal having no such “monotonic” constraint. Objection 2) is also invalid: there is no scientific “monatonicity argument” for a virial expansioni in the paper we point out that all the evidence is that the virial coefficients of hard-core systems in higher dimensions, including discs, go negative and can stay negative. Objection 3) is again incorrect. The virial equation, with the coefficients defined using the Mayer cluster integrals, is an expansion about zero density which is everywhere continuous in all its derivatives. The ther- modynamic state function pressure, by contrast is not, it will exhibit discontinuities at phase transitions. Objection 4) appears to be prejudiced by the referee’s misunderstanding above, and his failure to look at the correlation data we present in Table 1 and Figure A1. You only need to look at the numbers in Table 1 to see the evidence for the closure is compelling, albeit em- pirical. This behavior in two-dimensions is anticipated by extrapolation from higher dimensions. The referee, moreover, appears not to have seen Reference [1] (the analogous science published in the JCP paper of the 3D hard-sphere fluid). Objection 5) could not be further from the truth! See LAN LarXiv: 0806.1109 [pdf] 2008 Title: Two-phase coexistence in the hard-disk model Authors: Leslie V Woodcock Comments: Hard-disk controversy. In fact, I have been interested in this phase transition for 30 years: see “Melting in two dimensions: determination of phase transition boundaries” (Cape, van Swol and Woodcock) Journal of Chemical Physics, Volume 73, 913-922 (l980). Referee B said: “This paper presents some numerol- ogy using the known virial coefficients to predict the behavior of hard disks at higher densities than the con- vergence of the known virial coefficients. Let me remind the authors that non-analytical behavior is not predict- able, such as phase transitions. Their results, though in- teresting, are purely speculative, consequently. I would suggest that the manuscript be considered for publication in Physical Review E” Please read the paper beyond the abstract? Referee A again (9-point reply): 1) “The rebuttal letter of the authors emphasizes in many places that the virial expansion will not agree with the genuine thermodynamic equation-of-state beyond the point of the first order fluid solid transition. This is, in fact, exactly the reason which this present study is of very little interest because all of the interesting behavior which the authors report is indeed in the region where the virial expansion no longer represents the physics of the situation. 2) The authors rebuttal letter contains the following phrase “PRL is not a review article; it would be inappro- priate to cite the many previously proposed equations of state of the hard disc fluid.” I find this sentence to be extremely unprofessional. ALL scientific publications have an absolute requirement to fully credit existing work in the field. To say that a PRL is exempt from this mandatory requirement is to diminish the scientific  L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 629 credibility of the journal and must not be allowed. The authors MUST demonstrate that their approach is correct and the previous work is wrong. 3) The response to referee B is also very peculiar where the author say that “a full PRE paper at this stage is inappropriate.” It is my understanding the articles in PRL are NOT supposed to be preliminary reports based on partial or incomplete analysis but instead are intended to be reports of completed research of exceptional inter- est. The authors' response clearly demonstrates that the research does not meet the criteria of being fully com- pleted. 4) I do agree with the criticism made by referee B that the results are purely speculative. In my opinion purely speculative articles should not be published in PRL. 5) The authors claim in their rebuttal letter that “all evidence is that the virial coefficients of hard core sys- tems in higher dimensions go negative and can stay negative.” In the paper they say that “virial coefficients for all hard hyper-spheres of higher dimensionality than one eventually go negative.” This latter statement is not true. In all computed cases the virial coefficients of odd order are all positive. 6) In 2 dimensions there is a long standing contro- versy as to whether or not there is a first or a second order phase. This historical fact should be given refer- ence. Indeed, there is no proof that a crystalline phase exists at all (although there is also no proof that a crys- talline phase is impossible either). 7) The authors assume without giving any reason at all that the leading singularity in the virial expansion is at the closest packing density and their conclusion that the virial coefficients become and stay negative is driven by this assumption. From the analysis of the Percus Yevick equation it is quite likely that in odd dimensions higher than the leading singularity is on the NEGATIVE density axis which is consistent with the alternating signs of the virial coefficients in dimensions 5 and higher. Since a leading singularity at negative density has nothing to do with close packing this referee does not see why for dimensions 2 and 3 the leading singular- ity can be assumed to be at close packing. 8) In the opinion of this referee this entire paper is built on the assumption that the leading singularity in 2 dimensions is at close packing. Because this is a pure assumption the second referee is completely correct in pointing out that this paper is very speculative. 9) It is disingenuous of the authors not to give refer- ence to the many papers which do not make this as- sumption and predict virial coefficients which are all positive. The authors are in effect claiming that most of the literature on approximate equations of state is wrong. I believe that if this were made clear by the authors that the editors of PRL would agree that unless the authors can clearly explain why they are right and where so many others are wrong that the paper does not meet the standards of the journal.” Point 1 is a U-turn; Referee A evidently conceding his original misapprehension, now turns towards political, i.e. non scientific, reasons for rejection. Points 2 and 3 are new, and non-scientific. Point 4: the Referee A again misconstrues an empiri- cal observation as some theoretical “assumption”! There is no theoretical “assumption”, as there is, for example, in the Percus Yevick theory and similar theories of sim- ple liquids. Point 5: the statement that “virial coefficients can, and in some will, go negative and stay negative” is cor- rect and verifiable. Point 6: scientists seeking to publish discoveries should not be bound as a condition of publication to make reference to irrelevant and often unprincipled, scientific theory or scientific scams. There is now wide acceptance by most principled scientists in the field of statistical thermodynamics of condensed matter that the work that this referee A keeps insisting we refer to, was at best, a pie-in-the-sky theory, at worst a scam. Point 8: there is nothing “speculative” about 1) an empirical observation [Table 1 Figure A1] 2) an exact mathematical derivation [Equation 4, APPENDIX 1], and 3) a comparison with “experiment” (MD) [ Figure A2 and A3.] In fact, there is no speculation in this paper at all. Point 9: it is nothing to do with “standards”; it is about discovering, albeit by empirical means, the correct equation of state that reproduces the thermodynamic pressure with the 6-figure accuracy that it can now be computed up to the first thermodynamic phase transi- tion. Referee B again (reply): My review stands. The other reviewer basically has the same objections as I and his reply saying that his remarks only apply to the theoreti- cal virial expansion does not make the paper physically meaningful, though still of some interest. B still hasn’t read the paper! (new) Referee C said: “I basically agree with all the comments of referee A and do not find the author's re- sponse persuasive at all. I do not recommend publication of this paper.” Comment 2. “I am particularly concerned by points (original objections) 3 and 4 raised by Referee A. Indeed, in objection 3, referee A correctly points out that if there is a phase transition at some density, then the virial ex- pansion should have a singularity exactly at this density. This is well known in statistical physics, for instance in the study of the high temperature or high field expansion  L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 630 of the 2-dimensional Ising model. On the contrary, in this paper, the authors suggest that there might be a phase transition while at the same time the low-density expansion should stay convergent. This is impossible” Comment 3: “In my opinion, the discrepancy between MD data and the equation of state proposed by the au- thors is only due to an inaccuracy of the extrapolation” And indeed (point 4 of referee A) the extrapolation of complex virial coefficients based only on the first 10 seems very dangerous. There are plenty of examples in the mathematical literature where such an extrapolation leads to completely wrong results” Comment 2 is basically agreeing with the original misapprehension of referee A, [Note: referee C doesn’t know that referee A has since changed his mind] Not only is it not “impossible”, but that is exactly what does happen. Moreover, this paper has nothing to do with phase transitions of lattice gases that do not have the same analytic virial expansion at zero density. Comment 3 is meaningless without a relevant exam- ple. (new) Referee D said: “The paper presents an equa- tion-of-state for the hard-disk liquid based on the first 10 virial coefficients and then notes that this equation devi- ates from the simulated area-pressure curve at a density of ~ 0.4, a value similar to that associated with the per- colation of free volume. I cannot recommend publication of the paper in PRL. My reasons are as follows: 1) The authors do not provide an explanation of the deviation they report. The connection with the Ree - Hoover results are an interesting speculation. 2) The authors fail to make any case for the signifi- cance of their work. Even if one went beyond their paper and regarded the connection between their observed de- viation and the Ree-Hoover percolation as having been established, why would this be important? I do not mean to imply that it would not be important, merely that the authors seem to have taken it for granted that the sig- nificance is obvious.” Point 1 overlooks the explanation based upon a change in density fluctuation Point 2 is also incorrect; there is no “speculation”; it is an empirical result! There’s always a chance that could be an unfortunate coincidence but when you look at the science, it’s highly unlikely. Referee A again said, in response to a request to sup- ply an example of the references he repeatedly insists must be cited) “The theory of 2 dimensional melting has a large lit- erature not referred to by the authors. Some relevant papers are 1) Kosterlitz and Thouless, J. Phys. C6 (1973) 1181-1203; 2) Halperin and Nelson, Phys. Rev. Lett. 41 (1978) 121-124; 3) Nelson and Halperin, Phys. Rev. B 19 2457-2484; 4) Binder, Sangupta and Nielaba, J. Phys. Cond. Matt. 14 (2002) 2323-2333. To write on hard discs without making contact with this long standing problem is not acceptable. The authors have assumed that the virial expansion has its leading singularity at the close packed density. If this were correct then there is no Kosterlitz Thouless transition and no hexatic phase. The authors have not presented evidence to support this” There is no “longstanding problem”. In fact, the paper has nothing to do with 2-dimensional melting, let alone the fictitious “hexatic mesophase” to which referee A refers. Papers 1) to 3) above do not withstand scrutiny: the approximations in paper 1) and several of the equa- tions in papers 2) and 3) cannot be validated. Papers 3) above are effectively a scientific fraud that unfortunately caught the imagination of a lot of “band-wagoners” who, over 30 years since, have published a lot of papers that tell us nothing, see e.g. paper 4) above. “Furthermore the conclusion is based on assumed form for the large n behavior of the virial coefficients Bn which leads to the conclusion for large n the virial coef- ficients Bn will all be negative. This is a very strong conclusion which 1) is totally dependent on their as- sumed form and 2) is at variance with every other as- sumed form of the virial coefficients in the literature. In my opinion the authors do not give sufficient evidence to support this conclusion.” The form of Bn – Bn-1 as a function of n, is not “as- sumed”, as the data in columns 3 - 4 of Table 1 confirm, it is an empirical result. Arbitration Report by PRL Divisional Associate Editor: J. Machta (Nov. 2010) “The authors have proposed a closed form equation of state for 2D hard disks based on a fit to the known virial coefficients. This paper provides an accurate equation of state for hard disks that will be useful to workers in the field. It also gives evidence for two interesting conjec- tures: 1) the virial coefficients eventually become nega- tive and 2) there is a free volume percolation transition with thermodynamic consequences as proposed some time ago by Hoover. Although this paper is interesting and should be published, I do not recommend publica- tion in PRL. The manuscript has been reviewed by four independent, expert referees in the field. All of the refe- rees definitively recommend against publication in PRL. I am in agreement with the referees that the paper does not meet the standards for publication in PRL. 1) A fitted equation of state by itself is not of suffi- ciently broad interest to warrant publication in PRL. 2) I agree with the referees that the breakdown of the virial equation of state and its relation to Hoover’s pro- posal is too speculative for publication in PRL. To be 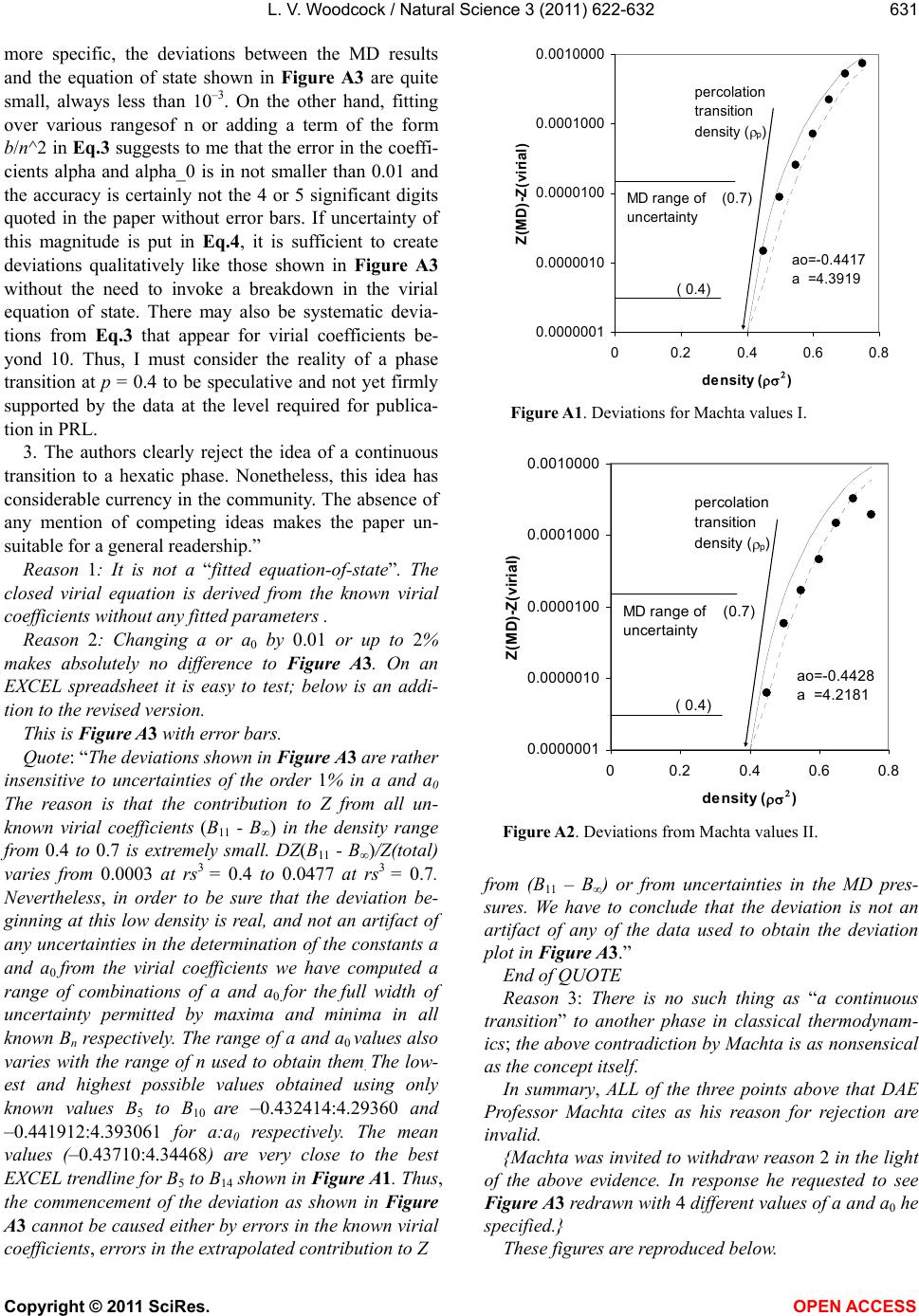 L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 631 more specific, the deviations between the MD results and the equation of state shown in Figure A3 are quite small, always less than 10–3. On the other hand, fitting over various rangesof n or adding a term of the form b/n^2 in Eq.3 suggests to me that the error in the coeffi- cients alpha and alpha_0 is in not smaller than 0.01 and the accuracy is certainly not the 4 or 5 significant digits quoted in the paper without error bars. If uncertainty of this magnitude is put in Eq.4, it is sufficient to create deviations qualitatively like those shown in Figure A3 without the need to invoke a breakdown in the virial equation of state. There may also be systematic devia- tions from Eq.3 that appear for virial coefficients be- yond 10. Thus, I must consider the reality of a phase transition at p = 0.4 to be speculative and not yet firmly supported by the data at the level required for publica- tion in PRL. 3. The authors clearly reject the idea of a continuous transition to a hexatic phase. Nonetheless, this idea has considerable currency in the community. The absence of any mention of competing ideas makes the paper un- suitable for a general readership.” Reason 1: It is not a “fitted equation-of-state”. The closed virial equation is derived from the known virial coefficients without any fitted parameters . Reason 2: Changing a or a0 by 0.01 or up to 2% makes absolutely no difference to Figure A3. On an EXCEL spreadsheet it is easy to test; below is an addi- tion to the revised version. This is Figure A3 with error bars. Quote: “The deviations shown in Figure A3 are rather insensitive to uncertainties of the order 1% in a and a0 The reason is that the contribution to Z from all un- known virial coefficients (B11 - B∞) in the density range from 0.4 to 0.7 is extremely small. DZ(B11 - B∞)/Z(total) varies from 0.0003 at rs3 = 0.4 to 0.0477 at rs3 = 0.7. Nevertheless, in order to be sure that the deviation be- ginning at this low density is real, and not an artifact of any uncertainties in the determination of the constants a and a0 from the virial coefficients we have computed a range of combinations of a and a0 for the full width of uncertainty permitted by maxima and minima in all known Bn respectively. The range of a and a0 values also varies with the range of n used to obtain them. The low- est and highest possible values obtained using only known values B5 to B10 are –0.432414 :4.29360 and –0.441912:4.393061 for a:a0 respectively. The mean values (–0.43710:4.344 68) are very close to the best EXCEL trendline for B5 to B14 shown in Figure A1. Thus, the commencement of the deviation as shown in Figure A3 cannot be caused either by errors in the known virial coefficients, errors in the extrapolated contribution to Z 0.0000001 0.0000010 0.0000100 0.0001000 0.0010000 00.2 0.4 0.60.8 density ( ) Z(M D)-Z(v irial) MD range of (0.7) uncertainty ( 0.4) percolation transition density ( p ) ao=-0.4417 a =4.3919 Figure A1. Deviations for Machta values I. 0.0000001 0.0000010 0.0000100 0.0001000 0.0010000 00.20.4 0.6 0.8 density ( ) Z(M D)-Z(virial) MD range of (0.7) uncertainty ( 0.4) percolation transition density ( p ) ao=-0.4428 a =4.2181 Figure A2. Deviations from Machta values II. from (B11 – B∞) or from uncertainties in the MD pres- sures. We have to conclude that the deviation is not an artifact of any of the data used to obtain the deviation plot in Figure A3.” End of QUOTE Reason 3: There is no such thing as “a continuous transition” to another phase in classical thermodynam- ics; the above contradiction by Machta is as nonsensical as the concept itself. In summary, ALL of the three points above that DAE Professor Machta cites as his reason for rejection are invalid. {Machta was invited to withdraw reason 2 in the light of the above evidence. In response he requested to see Figure A3 redrawn with 4 different values of a and a0 he specified.} These figures are reproduced below. 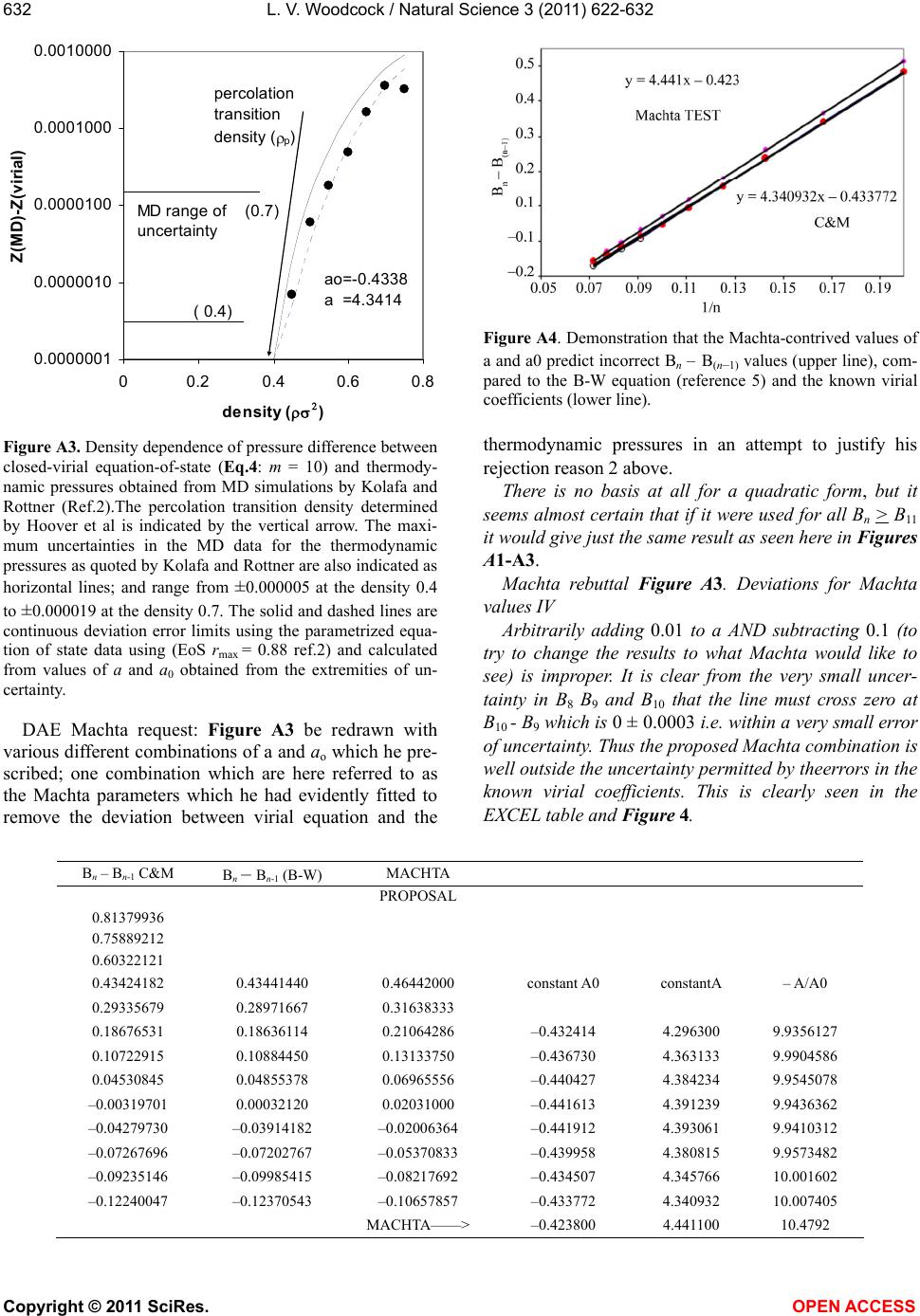 L. V. Woodcock / Natural Science 3 (2011) 622-632 Copyright © 2011 SciRes. OPEN ACCESS 632 0.0000001 0.0000010 0.0000100 0.0001000 0.0010000 00.20.4 0.6 0.8 density ( ) Z( MD)-Z ( virial) MD range of (0.7) uncertainty ( 0.4) percolation transition density ( p ) ao=-0.4338 a =4.3414 Figure A3. Density dependence of pressure difference between closed-virial equation-of-state (Eq.4: m = 10) and thermody- namic pressures obtained from MD simulations by Kolafa and Rottner (Ref.2).The percolation transition density determined by Hoover et al is indicated by the vertical arrow. The maxi- mum uncertainties in the MD data for the thermodynamic pressures as quoted by Kolafa and Rottner are also indicated as horizontal lines; and range from ±0.000005 at the density 0.4 to ±0.000019 at the density 0.7. The solid and dashed lines are continuous deviation error limits using the parametrized equa- tion of state data using (EoS rmax = 0.88 ref.2) and calculated from values of a and a0 obtained from the extremities of un- certainty. DAE Machta request: Figure A3 be redrawn with various different combinations of a and ao which he pre- scribed; one combination which are here referred to as the Machta parameters which he had evidently fitted to remove the deviation between virial equation and the Figure A4. Demonstration that the Machta-contrived values of a and a0 predict incorrect Bn – B(n–1) values (upper line), com- pared to the B-W equation (reference 5) and the known virial coefficients (lower line). thermodynamic pressures in an attempt to justify his rejection reason 2 above. There is no basis at all for a quadratic form, but it seems almost certain that if it were used for all Bn > B11 it would give just the same result as seen here in Figures A1-A3. Machta rebuttal Figure A3. Deviations for Machta values IV Arbitrarily adding 0.01 to a AND subtracting 0.1 (to try to change the results to what Machta would like to see) is improper. It is clear from the very small uncer- tainty in B8 B 9 and B10 that the line must cross zero at B10 - B9 which is 0 ± 0.0003 i.e. within a very small error of uncertainty. Thus the proposed Machta combination is well outside the uncertainty permitted by theerrors in the known virial coefficients. This is clearly seen in the EXCEL table and Figure 4. Bn – Bn-1 C&M Bn – Bn-1 (B-W) MACHTA PROPOSAL 0.81379936 0.75889212 0.60322121 0.43424182 0.43441440 0.46442000 constant A0 constantA – A/A0 0.29335679 0.28971667 0.31638333 0.18676531 0.18636114 0.21064286 –0.432414 4.296300 9.9356127 0.10722915 0.10884450 0.13133750 –0.436730 4.363133 9.9904586 0.04530845 0.04855378 0.06965556 –0.440427 4.384234 9.9545078 –0.00319701 0.00032120 0.02031000 –0.441613 4.391239 9.9436362 –0.04279730 –0.03914182 –0.02006364 –0.441912 4.393061 9.9410312 –0.07267696 –0.07202767 –0.05370833 –0.439958 4.380815 9.9573482 –0.09235146 –0.09985415 –0.08217692 –0.434507 4.345766 10.001602 –0.12240047 –0.12370543 –0.10657857 –0.433772 4.340932 10.007405 MACHTA––––> –0.423800 4.441100 10.4792
|