Modern Economy, 2011, 2, 354-370
doi:10.4236/me.2011.23039 Published Online July 2011 (http://www.SciRP.org/journal/me)
Foreign Exchange Reserves Demand Model
Based on Chinese Government Utility
Maximization and Analysis of Chinese Fore ign
Exchange Reserves*
Shihong Zeng
School of Economics & Management, Beijing University of Technology, Beijing, China
Received April 15, 2011; revised April 25, 2011; accepted June 3, 2011
Abstract
At the end of 2010 China’s foreign exchange reserve reached $2847.34 billion, the author designs the maxi-
mum government utility function when consider the China government buys a part foreign exchange if
company earns, it means that the China government will increase Ren-Min-Bi Yuan. And it will cause infla-
tion. The inflation will cause disutility to government. Finally it gets the optimal fuction. VAR Regress finds
the fitted value and actual value of foreign exchange reserves is nearly equal within 99.8%. The thesis gets
the long term equilibrium relation of the nature logarithm of variables by VEC model, which are foreign ex-
change reserves, standard error of export, marginal propensity to import, the opportunity cost for foreign ex-
change reserves, marginal output to export. Using the sample datas in China 1980-2006 and VEC, we can
find that 1) the government-holding foreign exchange reserves has positive correlation with the export stan-
dard error, 2) the government-holding foreign exchange reserves has positive correlation with the marginal
propensity to import. The data and regression method are all different, but all have the positive correlation
between the foreign exchange reserves and export standard error.
Keywords: Foreign Exchange Reserves, Demand Model, Chinese Government, Utility Maximization
1. Introduction
This template, In order to study demand model of op-
timal foreign exchange reserves based on Chinese
government utility maximization and analysis of Chi-
nese foreign exchange reserves, the thesis arranges as
the followings: the first section designed the demand
model of optimal foreign exchange reserves based on
Chinese government utility maximization, the second
section analyzed the unit root test and cointegration of
optimal foreign exchange reserves based on govern-
ment utility maximization, the third section analyze
VAR and VEC model of optimal foreign exchange
reserves based on government utility maximization, the
fourth section is the summary of this thesis.
2. Demand Model of Optimal Foreign
Exchange Reserves Based on Chinese
Government Utility Maximization
In order to study the demand model of optimal foreign
exchange reserves based on Chinese government utility
maximization, the thesis arrange as the followings: First,
the authors analyzes the significance and objectives of
the research, then review the literature simply. Based on
Kelly, Michael G. (1970), consider the China govern-
ment buy part foreign exchange as oreign exchange re-
serves if company earn oreign exchange, it means that
the China government will increase supply of Ren-Min-
Bi Yuan, and it will cause inflation. The inflation will
cause disutility to government that is a negative govern-
ment utility, combining with the outputting fluctuation,
the foreign exchange reserves make the resource to be
unused and lead to a negative social welfare, then design
the following government utility function. Finally get the
*This work was achievements of the current stage of 2010 Statistical
Science key research program of China (No. 2010LB33) and 2010
talent to deepen teaching plan in Beijing University of Technology
(01100054R6002).

S. H. ZENG355
demand model of optimal foreign exchange reserves based
on government utility maximization.
2.1. Significance and Objectives of the Research
2.1.1. Researc h Sig ni fi ca nce
December 31, 2003, the Chinese government completed
the capital injection of $45 billion foreign exchange re-
serve into Bank of China and Bank of Construction. This
capital injection played a substantial role in stabilizing
and strengthening China’s domestic banks. At the end of
2010 China’s foreign exchange reserve reached $2847.34
billion, which had played an important role in supporting
Chinese REN MIN BI YUAN (RMB) appreciation. In an
open economy, a foreign exchange reserve is an impor-
tant index to study a country’s international economic
relations; it reflects results of the macroeconomic opera-
tion and functions as an important means of macroeco-
nomic control. The foreign exchange reserve in fact af-
fects many aspects of macro economy: it helps to under-
stand a country’s macroeconomic operation; the adjust-
ment of the reserve level can achieve domestic and in-
ternational economic balances and realize the established
macroeconomic objectives. A country’s foreign exchange
reserve should fit its actual economic development. A
sufficient foreign exchange reserve can ensure a coun-
try’s international payment capability, its ability to in-
tervene in the foreign exchange market, as well as its
international credibility. At the same time, an excessive
foreign exchange reserve can lead to the waste of its re-
sources. This is because owning a sizable foreign ex-
change reserve by a country means providing foreign
countries with some of its own resources while giving up
opportunities to use foreign recourses to increase its do-
mestic investment and economic development. It is true
that a limited foreign exchange reserve will negatively
affect domestic economic development, the govern-
ment’s capabilities to intervene in the foreign exchange
market and to balance international revenue and expen-
diture. All this can weaken a country’s capability to meet
international capital shock and to avoid financial crisis,
which will not help, in our case, China’s financial enter-
prises/companies to ‘get into the world.’ Therefore, the
study of the optimal scale of a country’s foreign ex-
change reserve is crucial to the country’s credibility, sta-
bility as well as to understanding the international finan-
cial environment into which Chinese financial enter-
prises/companies are entering.
2.1.2. Research Objectives
The thesis finishes the following researches, the author
designs the maximum government utility function when
consider the China government buys part foreign ex-
change if company earns, it means that the China gov-
ernment will increase Ren-Min-Bi Yuan, and it will
cause inflation. The inflation will cause disutility to gov-
ernment. Then it gets the optimal foreign exchange re-
serves. Finally unit root test, cointegration test, vector
autoregressive model analysis, vector error correction
model analysis and the long term equilibrium relation of
the variables which the optimal foreign exchange re-
serves function include.
2.2. Literature Review
The Heinz Robert Heller (1966) constructed the demand
of reserves. Heller’s model is the beginning of cost reve-
nue. After that time, many scholars have developed
Heller’s pattern and obtained their results. He pointed out
that holding the reserves exist opportunity cost. The ex-
pression is the loss of investment benefit owing to hold-
ing reserves. When marginal cost equals to marginal pro-
ceeds，international reserve achieved the proper scope [1].
Clark (1970) has extended Heller’s method and de-
veloped a random pattern, considered the opportunity
cost for holding foreign exchange reserves, then con-
structed the government utility function. He reached: 1)
the random error item of standard error has positive cor-
related between foreign exchange reserves and optimal
foreign exchange reserves; 2) It has negative correlated
between optimal foreign exchange reserves and marginal
propensity to import; 3) The opportunity cost for holding
foreign exchange reserves more, the optimal foreign ex-
change reserves less [2].
Kelly. Michael G. (1970) thought that holding foreign
exchange reserves has an opportunity cost. According to
this, he constructed the utility function. At last, he
achieved the optimal foreign exchange reserves function
be means of the utility function. He found that there has
positive correlated between the foreign exchange re-
serves holding by government and the standard error of
export, in the same time has positive correlated with the
average propensity to import [3].
Guobo Huang (1995) has collected the economic data
about China during 1980 to 1990. He researched the in-
ternational reserve scale of China by using of ECM and
discovered that: 1) The Chinese foreign exchange reserve
has the negative correlation with import, that is when the
import increased the foreign exchange reserves will re-
duce; 2) It has negative correlation with average propen-
sity to import, that is when the average propensity to
import increased the foreign exchange reserves will re-
duce; 3) The Chinese government has an ability to adjust
the foreign exchange reserves, but the ability will reduce
without considering the net foreign exchange reserves of
China Bank [4].

S. H. ZENG 356
Yu Yongding (1997) found Chinese foreign exchange
reserves are higher than reasonable and optimal foreign
exchange reserves [5].
Wu (1998) combined the ratio analysis method and the
factor analysis method to study the determinant of rea-
sonable Chinese foreign exchange reserves. He assumed
that the Chinese demand foreign exchange reserve con-
sists of four aspects: foreign exchange demanded for
imports, foreign exchange demanded for repaying the
total foreign debt balance, exchange demanded for prof-
its return from foreign direct investment and foreign ex-
change reserves demand for the country’s intervention in
the foreign exchange currency market. He also estab-
lished a linear equation model. The purpose of his thesis
was to determine reasonable foreign exchange reserves
for China, so he did not determine the equation’s pa-
rameters with time-serial data or test the equation [6].
According to Xu (2001), the amount of currency in
circulation imposes a more notable impact on the foreign
exchange reserve in the short-term than does money and
quasi-money. In addition, he also found that a long-term
equilibrium relationship between the average propensity
to import and the demand for foreign exchange reserves
does not exist, yet the variation of a short-term average
propensity to import exerts comparatively notable nega-
tive impacts on foreign exchange reserves. The reason is
that under the current foreign exchange supervision sys-
tem, an increase in imports means that a country would
have to sell more foreign exchange, which would result
in a decrease in the volume of foreign exchange reserves
that are held [7].
Victoria miller (2006) support China to use foreign
exchange reserves to save Chinese banks and Asian bank
[8]. M. Ramachandran (2006) finds the asymmetric con-
trol over capital flows and asymmetric intervention in
favour of strengthening export competitiveness in an era
of persistent capital inflows seem to be responsible for
large stockpile of reserves in India [9].
Adnan Kasman and Duygu Ayhan (2008) find that
exchange rate Granger causes foreign exchange reserves
in the long-run nominal [10].
Victor Pontines and Ramkishen S. Rajan (2011) find
that Asian central banks react more strongly to currency
appreciations than depreciations and more to nominal ef-
fective exchange rates (NEERs) than to bilateral US dollar
rates. This rationalizes the relative exchange rate stability
and the sustained reserve accumulation in the region [11].
2.3. Design of Government Utility Function
2.3.1. Kelly, Michael G. (1970) Design of Government
Utility Function
Kelly, Michael G. (1970) designed the government util-
ity function without considering the China government
buys part foreign exchange if company earn, it means
that the China government will increase Ren-Min-Bi
Yuan, and it will cause inflation. The inflation will cause
disutility to government.
Because the change of foreign exchange reserves
equal to export increment subtract import increment, so
RtXt Mt

  (1)
where R is the foreign exchange reserves, X is the export,
M is the import.
Suppose that the reaction coefficient of import to ex-
port is dd
f
MX

. Suppose that the reaction coeffi-
cient of income to export is dd
g
YX，where Y is
income
Because the marginal propensity to import is
ddmMY

So


dddd dd
f
MX mgMYYX
From Equation (1) we have

1RX f 

(2)



 
2
21VRE RVXf  (3)
V is the variance in Equation (3); Equation (3) suggests
that: the variance of foreign exchange reserves equal to
the expectation of the squared of change amount of for-
eign exchange reserves
Use the same arguments that:




22
VYEYgV X  (4)
dd
g
YX

in Equation (4), where Y is income
The government won't hope to run out the foreign ex-
change reserves, or we can say that the government hope
keep lowest foreign exchange reserves R¹, so its target is
to keep enough foreign exchange reserves as more as
they can, to make it almost impossible that the foreign
exchange reserves they kept lower than their target
amount R¹, and satisfied the following Equation,
 
1,PRRER VRe




(5)
e in Equation (5) is a very minor number, for any arbi-
trarily given and ruled probability density function, arbi-
trarily given e, educes
 
ddER VR0
, which sug-
gests that if the variance of foreign exchange reserves is
greater, in order to keep a arbitrarily given probability e
of the ruled foreign exchange reserves R¹, the average of
foreign exchange reserves required is greater.
Suppose that probability e is positive with V(R), and is
negative with E(R)2, gives:
 
20ecVRER

 (6)
Equation (6) has characteristic that () 0eER ,
22
() 0eER

 ,() 0eVR

, and for the arbitrarily

S. H. ZENG357
given e,
 
ddER VR0, from Equation (3) and
Equation (6) we can get the average level of foreign ex-
change reserve is that,
     
1212 1ERceSRce SXf  (7)
where S(X) is the standard error of the export X
From Equation (4) we can get



g
SYS X, put
f
mg and
 
g
SYS X into Equation (7),
  
12
ERceSX mSY



 (8)
Because keeping amount of foreign exchange reserve
means the resource being left unused, so it may make
output reduced, so the output that the relationship of the
government whether keep foreign exchange reserve is,
1
YYRi (9)
where Y¹ is the output of government does not hold for-
eign exchange reserve, Y is the output of government
hold foreign exchange reserve, where R is foreign ex-
change reserve, i is the opportunity cost for holding for-
eign exchange reserves.
Kelly, Michael G. (1970) designed the following gov-
ernment utility fuction.

 
22
1
UaEYEYbYEY

 


2.3.2. Considered the Inflation Made by the Chinese
Government Buy Part Foreign Exchange If
Company Earn and Design the Government
Utility Function
Based on Kelly, Michael G. (1970), consider the Chinese
government buy part foreign exchange if company earn,
it means that the Chinese government will increase sup-
ply of Ren-Min-Bi Yuan, and it will cause inflation. The
inflation will cause disutility to government that is a
negative government utility.
Combining with the outputting fluctuation, the foreign
exchange reserves make the resource to be unused and
lead to a negative social welfare, then design the follow-
ing government utility function.

 
22
1
UaEYEYbYEY 

 




 (10)
where β > 0 is a coefficient,

is the inflation,

 is
change amount of inflation or increasing amount.
is the average fluctuation outputs when
government does not hold foreign exchange reserve and
hold foreign exchange reserve, is the
fluctuation of outputs and average outputs.



1
EY EY

2
 

YEY
2
R    , δ > 0 is a coefficeint
 
22
VYY EYSY  

(11)


  
2
2
2
22
2
2
dd
d1-
d1
MX
XE
X
Xf
RR M
X
   





(12)
0d



 in Equation (12)
 

2
VXX EX

(13)
Put Equation (4)





22
VYEYgV X  into
Equation (13)
 
2
22
VXVY gSYg (14)
Put Equations (9)-(13) into Equation (10), then gets
the expectation efficacy function



 
 
  
 
2
1
2
2
22
22
2
1
21
EUa EYEY
bY EY
ai ERbV Y
dX EXf
ai ERbV YdVXf


 



 
 
 2
(15)
Put Equation (14) in Equation (15), gives:
 
2
22 2
21EUaiERbSYdSYgf 
 


2
2.4. Demand Model of Optimal Foreign
Exchange Reserves Based on Chinese
Government Utility Maximization
Choose variable E(R) and S(Y), and combine with the
constraint condition Equation (8) and design the fol-
lowinig F fuction.
 
 

2
22 2
21
12
2
F
aiERbS YdSYgf
ERceSX mSY 

 


 



2
() 20FER aiER 

 (16)
 

 

2
22
1/2
2
1/2
() 221
221
0
F
SYbS YdSYgf
ce m
bS YdS Yfg
ce m



 



 



(17)
From Equation (16) gets:

2aiE R   (18)
Put Equation (18) in Equation (17)

S. H. ZENG 358
 

2
1/2
2
22
0
1bS YdS Yfg
aiRcemE
 


 (19)
As a matter of convenience, arranges h as the follow-
ings

1/2
hce (20)
From Equation (19) and Equation (20) gets
 

2
21SYai ERhmbfgd



 (21)
Put Equation (21) in Equation (8)


 
 

2
21
ER
hSXmai ERhmbfgd

 

(22)
From Equation (22) gets






2
122 1
ER
SXhaimhbf g d



 
 
(23)
Put dd
f
MX mg in Equation (23)


 

2
122 1
ER
SXhaimhbgm d










(24)
Because of

2
2
12
ER
DF ai0
So
  

2
22
2
22
1
22210
DFER FSYFERSY
aibdf g


 



Conditions as above satisfied binary function approach
maximum, that is the government expectation efficacy
function E(U) exist a maximum, the optimal foreign ex-
change reserves based on government utility maximiza-
tion could fixed by Equation (24).
Be convenient order, let

2
22 1
1khaimhb gmd



 



 (25)

2
1
wb gmd

  (26)
2.5. Analyze the Optimal Expectation Foreign
Exchange Reserve to the Sensitivity of
Variable and Parameter Based on
Government Utility Maximization
The foreign exchange reserve which government expec-
tation utility maximization E(U) exist a maximum is the
optimal expectation foreign exchange reserve E(R), to
the sensitivity


ER g

of reaction coefficient
dd
g
YX

that income to export, approach the partial
derivative.




22122 2
2
ER g
SXhai mdgmgkw





(27)
When 10gm


, that is dd1fMXmg




22122 2
20
ER g
SXhaim dgmgkw






(28)
When 10gm


, that is ddfMXmg1




22122 2
20
ER g
SXhaim dgmgkw






(29)
When 10gm


, that is ddfMXmg1




22122 2
20
ER g
SXhaim dgmgkw






(30)
So the sensitivity


ERg

of reaction coefficient
(ddgYX

) that optimal foreign exchange reserve to
reaction coefficient that import to export is depend on the
size of
f
mg

, that is depend on the size of the reac-
tion coefficient dd
f
MX

that import to export.
The optimal foreign exchange reserve susceptibility


ER m

 to the marginal propensity to import


ddm
M
Y, approach the partial derivative.


 

2222 2
2
ER m
SXhaimbdgmdgkw





(31)
When



12
1bdmggdf g


 




 

2222 2
20
ER m
SXhaimbdgmdgkw




 

(32)
When



12
1bdmggdf g


 




 

2222 2
20
ER m
SXhaimbdgmdgkw






(33)
When



12
1bdmggdf g


 




 

2222 2
20
ER m
SXhaimbdgmdgkw




 

(34)
The optimal expectation foreign exchange reserve sus-
ceptibility




ER SX to the export standard devia-
tion S (X), approach the partial derivative,

S. H. ZENG 359



1ER SXk (35) X1 is the export amount per year (Dimension of R, X2,
S (X), M, dM is 100 million RMB Dollars)
because

2
122 1
khaimhb gmd

, so: X2 is the export amount per year
dX2 is the export increasing amount per year



1ER SXk0 (36) E(X) is the average value of X2
S(X) is the absolute value of the deviation between the
average value of X2 and X2
The optimal expectation foreign exchange reserve sus-
ceptibility

ER i to the opportunity cost for gov-
ernment holding foreign exchange reserves i, approach
the partial derivative,
dM is the import increasing amount per year
Y2 is GDP =Y1/ER
  

2
22
21ERiSXhai ibfdg

 


0

(37)
dY2 is the GDP increasing amount per year
dd
g
YX

, g is the reaction factor from income to
export, where Y is income
2iyt yr

is the opportunity cost for holding foreign
exchange reserves, using the difference between profit
rate and the reserve earnings yield before capital tax in
China to compotator.
2.6. Brief Summaries
The thesis finishes the following researches:
1) The author designs the government utility function
when consider the China government buy part foreign
exchange if company earn, it means that the China gov-
ernment will increase Ren-Min-Bi yuan, and it will cause
inflation. The inflation will cause disutility to govern-
ment; 2) The thesis gets the optimal foreign exchange
reserves by Maximum the government utility.
2
y
t is the profit rate before capital tax in China.
yr is the reserve earnings yield, using one year treas-
ury bill rate-inflation rate in USA
y
rbrir
br is one-year Treasury bill yield rate in USA.
ir is the inflation in USA; take the yearly average in-
flation in USA as the standard.
The value of m, i ,g be changed to the positive value
when they are negative value by inserting reasonable value,
so we use datas as Appendix Table 1 to analyze unit root
( In order to convenient for readers, shown M, Y2, 2
y
t,
, , br ir
y
rbrir

, 2iyt y
3. Unit Root Test and Cointegration Analysis
for Demand Variable of Optimal Foreign
Exchange Reserves Based on Government
Utility Maximization
r

 in Appendix Table 2.
(The principle is, if the column datas m, g are –0.001,
–0.01, –1, –10, –100, then change to 0.1, 0.01, 0.001,
0.001, 0.0001. 0.0001, 0.000001; if the column data i is
–0.001, then change to 0.00001)
This thesis takes the unit root test and cointegration
analysis for demand variable optimal foreign exchange
reserves based on government utility maximization. 3.2. About the Unit Root Test for Variable
3.1. About Data and Express and Process for
Data LNR, LNSX, LNM, LNI, LNG, these variables’ defining
in several is
LNR = LOG (R); LNSX = LOG (SX)
In order to discuss conveniently, the authors use as the
following marks to express the different economic vari-
able in this thesis. Dimension of R, X2, S (X), M, dM is
100 million US Dollar
LNM = LOG (m); LNI = LOG (i); LNG = LOG (g)
That is, LNR, LNSX, LNM, LNI, LNG is the natural
logarithm value of R, SX, m, i, g, from Figures 1(a) and
(b). We can see that LNR, LNSX, LNM, LNI, LNG these
variables are very unstable.
R is the foreign exchange reserve in China
ER is equal to exchange rate
Table 1. The results of cointegration test for LNR, LNSX, LNM, LNI, LNG.
Eigenvalue Trace Statistics 5% level critical value1% level critical value The null hypothesis: the amount of cointegration equation
0.744664 87.44357 68.52 76.07 0**
0.660712 54.67939 47.21 54.46 be equal or less than 1**
0.557578 28.73762 29.68 35.65 be equal or less than 2
0.303918 9.165804 15.41 20.04 be equal or less than 3
0.019430 0.470908 3.76 6.65 be equal or less than4
The upper results express that there are exist 2 cointegration equations with a 5% significant level.

S. H. ZENG 360
Table 2. The value of AIC and SC for LNR, LNSX, LNM, LNI, LNG with K equal to 2, 3, 4.
AIC and SC LNR LNSX LNM LNI LNG
When K = 2 the results as follows,
Akaike AIC 0.615183 2.000989 4.456350 3.251926 6.414522
Schwarz SC 1.155124 2.540930 4.996291 3.791867 6.954464
When K = 3 the results as follows,
Akaike AIC -0.336246 2.073180 4.757156 3.469487 5.974624
Schwarz SC 0.453663 2.863089 5.547065 4.259396 6.764533
When K = 4 the results as follows,
Akaike AIC –12.38870 –4.499733 –0.183613 –3.185220 3.734113
Schwarz SC –11.34725 –3.458283 0.857836 –2.143770 4.775563
2
4
6
8
10
80 82 84 86 88 90 92 94 96 98 00 020406
LNR LNSX
-15
-10
-5
0
5
80 82 84 86 88 90 92 94 96 98 00 02 04 06
LNMLNILNG
Figure 1. (a) LNR, LNSX; (b). LNM, LNI, and LNG.
3.2.1. Unit Root Test for LNR
Sequence number ADF test DW
1) D (LNR) = 0.09218 + 0.01466 LNR (–1) + 0.46569 D (LNR (–1)) – 0.28970 D (LNR (–2)) 2.11
(0.341475) (0.319634) * (2.085069) (–1.406102)
2) D(LNR,2) = –0.52131D(LNR(–1))+ 0.12159 D(LNR(–1) ,2) –0 .02565D(LNR(–2),2) 1.69
(–2.052857) * (0.506699) (–0.121333)
3.2.2. Unit Root Test for LNSX
Sequence number ADF test DW
1) D (LNSX) = 0.002402 LNSX (–1) + 0.3243 35 D (LNSX (–1)) – 0.065271 D (LNSX (–2)) 2.00
(0.108364)* (1.479004) (–0.295998)
2) D(LNSX,2)= –0.7834 D(LNSX(–1 )) + 0.1059 D(LNSX(–1),2)+ 0.0627 D(LNSX(–2),2) 1.98
(–2.485189)* (0.387888) (0.277638)
3.2.3. Unit Root Test for LNM
Sequence number ADF test DW
1) D (LNM) = –0.143051LNM (–1) –0.835517D (LNM (–1)) –0.539727D (LNM (–2)) 1.74
(–0.971128)* (–4.473790) (–3.287342)
2) D(LNM,2)= –1.981791D(LNM(–1))+ 0.173656D(LNM(–1),2) –0.19828D(LNM(–2),2) 1.67
(–3.172415) * (0.389723) (–0.957421)
3.2.4. Unit root test for LNG
Sequence number ADF test DW
1) D (LNG) = –0.542661LNG (–1) –0.25572 8D (LNG (–1)) – 0.089202D (LNG (–2)) 2.17
(–2.255491)* (–1.092668) (–0.466460)
2) D(LNG,2) = –2.456410D(LNG(– 1)) + 0.72 6233D(LNG(–1),2 ) + 0.220260D(LNG(–2),2) 2.21
(–4.895653)* (1.992495) (1.146552)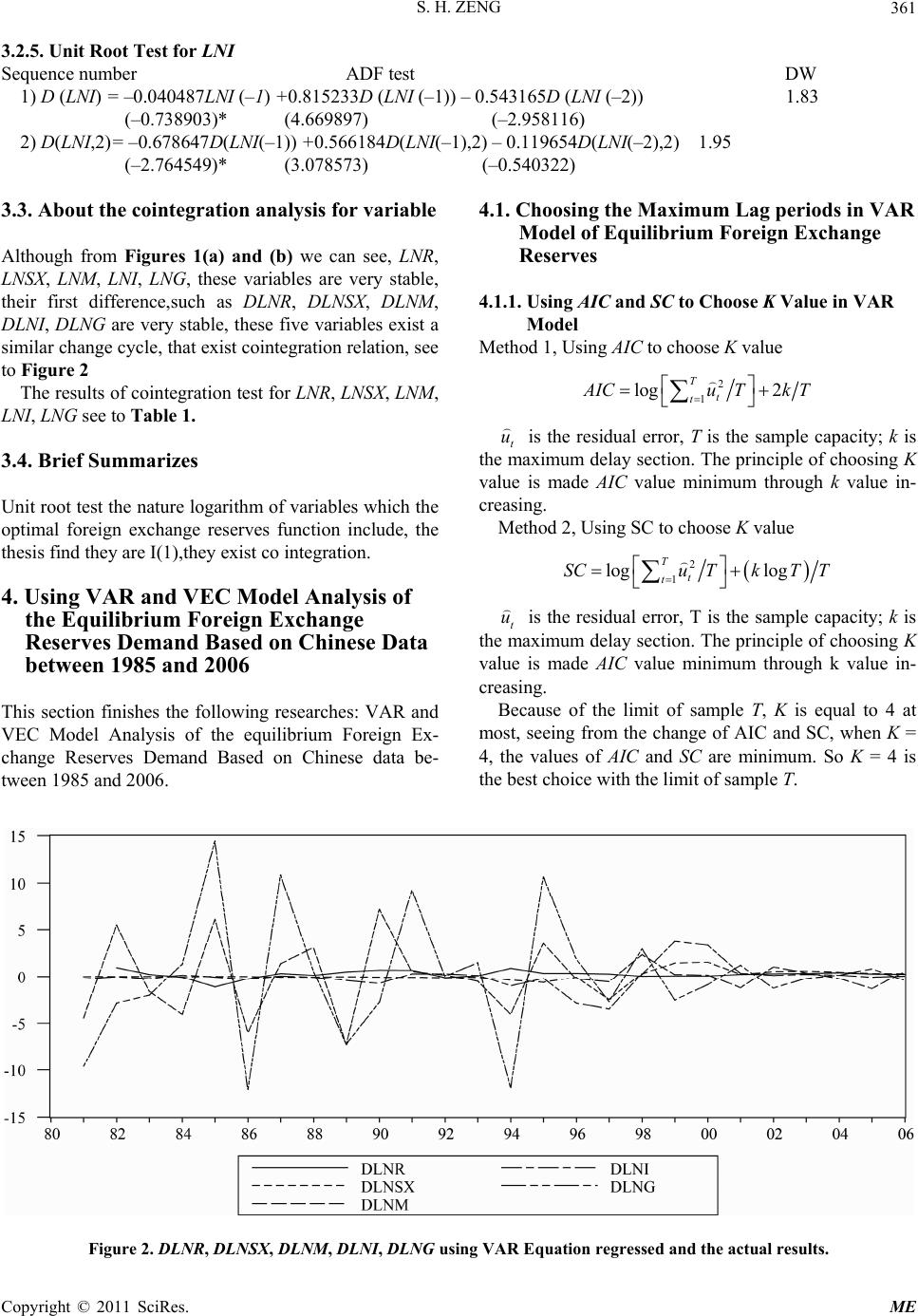

S. H. ZENG 361
3.2.5. Unit Root Test for LNI
Sequence number ADF test DW
1) D (LNI) = –0.040487 LNI (–1) +0.815233D (LNI (–1)) – 0.543165D (LNI (–2)) 1.83
(–0.738903)* (4.669897) (–2.958116)
2) D(LNI,2)= –0.678647D(LNI(–1)) +0.566184D(LNI(–1),2) – 0.119654D(LNI(–2),2) 1.95
(–2.764549)* (3.078573) (–0.540322)
3.3. About the cointegration analysis for variable 4.1. Choosing the Maximum Lag periods in VAR
Model of Equilibrium Foreign Exchange
Reserves Although from Figures 1(a) and (b) we can see, LNR,
LNSX, LNM, LNI, LNG, these variables are very stable,
their first difference,such as DLNR, DLNSX, DLNM,
DLNI, DLNG are very stable, these five variables exist a
similar change cycle, that exist cointegration relation, see
to Figure 2
4.1.1. Using AIC and SC to Choose K Value in VAR
Model
Method 1, Using AIC to choose K value
2
1
log 2
T
t
t
A
ICuTkT






The results of cointegration test for LNR, LNSX, LNM,
LNI, LNG see to Tab le 1.
t
u

is the residual error, T is the sample capacity; k is
the maximum delay section. The principle of choosing K
value is made AIC value minimum through k value in-
creasing.
3.4. Brief Summarizes
Unit root test the nature logarithm of variables which the
optimal foreign exchange reserves function include, the
thesis find they are I(1),they exist co integration.
Method 2, Using SC to choose K value

2
1
log log
T
t
t
SCu TkT T






4. Using VAR and VEC Model Analysis of
the Equilibrium Foreign Exchange
Reserves Demand Based on Chinese Data
between 1985 and 2006
t
u

is the residual error, T is the sample capacity; k is
the maximum delay section. The principle of choosing K
value is made AIC value minimum through k value in-
creasing.
Because of the limit of sample T, K is equal to 4 at
most, seeing from the change of AIC and SC, when K =
4, the values of AIC and SC are minimum. So K = 4 is
the best choice with the limit of sample T.
This section finishes the following researches: VAR and
VEC Model Analysis of the equilibrium Foreign Ex-
change Reserves Demand Based on Chinese data be-
tween 1985 and 2006.
Figure 2. DLNR, DLNSX, DLNM, DLNI, DLNG using VAR Equation regressed and the actual results.

S. H. ZENG 362
4.1.2. VAR Model of Equilibrium Foreign Exchange
Reserves Demand Based on C h in e se Data
Between 1985 and 2006
Because K = 4 is the best choice, VAR model of equilib-
rium foreign exchange reserves demand based on Chi-
nese data between 1985 and 2006 used K = 4, when the
variable delayed 4 sections, that is when K = 4 the
Equtions as follows,
LNR = 1.158208*LNR(–1) – 0.75956090 28* LNR(–2)
+ 1.275854675*LNR(–3) – 0.41874649*LNR(–4)
– 0.5326487006*LNSX(–1) + 0.04889939 537*LNSX(–2)
+ 0.272843226*LNSX(–3) – 0.039302859*LNSX(–4)
– 0.01712404005*LNM(–1) – 0.1990991828*LNM(–2)
– 0.1133346012*LNM(–3) – 0.03947680 86*LNM(–4)
+ 0.3329742763*LNI(–1) + 0.1276036813*LNI(–2)
– 0.1739915379*LNI(–3) + 0.0949172971*LNI(–4)
+ 0.0309059384*LNG(–1) + 0.071224 90 394*LNG(–2)
+ 0.05650023494*LNG(–3) + 0.01177553 108 *LNG(–4)
+ 1.07792509
LNSX = –3.938060 6*LNR(–1) + 3.35668*LNR(–2)
– 0.607910938*LNR(–3) + 0.5289359612*LNR(–4)
+ 1.752410011*LNSX(–1) + 0.7814465787*LNSX(–2)
– 0.96916476*LNSX(–3) + 0.3469152308*LNSX (–4)
+ 0.02346185581*LNM(–1) + 0.380843381*LNM(–2 )
+ 0.02583196853*LNM(–3) – 0.1368834866*LNM(–4)
– 0.2797186513*LNI(–1) – 1.013477322*LNI(–2)
+ 1.247770225*LNI(–3) – 0.455388757*LNI(–4)
– 0.05458893085* LNG(–1) – 0.0383 9642266*LNG(–2)
+ 0.1945562552*LNG(–3) + 0.2417625189*LNG(–4)
– 1.52559448
LNI = – 8.618872*LNR(–1) + 9.4407164*LNR(–2)
– 6.7190925*LNR(–3) + 3.102998318*LNR(–4)
+ 5.061829074*LNSX(–1) – 1.173982425*LNSX(–2)
– 1.455715567*LNSX(–3) + 2.734477293*LNSX(–4)
+ 0.6480708563*LNM(–1) + 1.557535337*LNM(–2)
+ 0.2412607597*LNM(–3) – 0.09576680591*LNM(–4)
– 2.139039105*LNI(–1) – 0.418124 08 94*LNI(–2)
+ 2.005046131*LNI(–3) – 1.968406804*LNI(–4)
– 0.342939926*LNG(–1) – 0.1883294592*LNG(–2)
+ 0.4212904271*LNG(–3) + 0.355278824*LNG(–4)
– 21.58283256
LNG = 14.175261*LNR(–1) – 18.4748659*LNR(–2)
+ 8.1032935*LNR (– 3) + 3.35 161008 *LNR(–4)
– 10.54483977*LNSX(–1) + 2.4 11978668*LNSX(–2)
+ 5.86210599*LNSX(–3) – 2.55802 967*LNSX(–4)
– 0.0052018235*LNM(–1) – 1.774668358*LNM( –2)
– 1.075279662*LNM(–3) – 1.741231895*LNM(–4)
+ 5.55427464*LNI(–1) – 0.99946 07549*LNI(–2)
– 2.685201432*LNI(–3) + 1.629023047*LNI(–4)
– 0.157488914*LNG(–1) – 0.1861 27449*LNG(–2)
– 0.8664866224*LNG(–3) + 0.02690099581*LNG(–4)
– 10.87342161
Using LNR equation in VAR equation set to forecast
the foreign exchange reserve in China (FR), the fore-
casting values of FR and the actual values of R are
shown in Figure 3 and Table 3.
See from Table 3 the forecast error is very minor, from
0.02% to 0.1%, and the forecasting is highly accurate,
from 99.98% to 99.99%.
4.2. VEC Model Estimation of Equilibrium
Foreign Exchange Reserves Demand Based
on Chinese Data Between 1985 and 2006
Because all the values LNR, LNSX, LNM, LNI, LNG are
I(1), also exist co integration, so exist a error correction
model.
4.2.1. Det e rm i n in g t h e Delay Section in the VEC
Model of the Equilibrium Foreign Exchange
Reserves Demand Based on t he C h in es e Data
between 1985 and 2006
Because when K = 1
Akaike Information Criteria 15.69124
Schwarz Criteria 17.65466
When K = 2
Akaike Information Criteria 13.59685
Schwarz Criteria 16.80585
Figure 3. The forecasting values of FR and the actual values of R.

S. H. ZENG363
Table 3. Forecast error between the value of FR and R.
obs RESID R FR ES
1985 0.01 26.44 26.435 0.0002
1986 0.01 20.72 20.709 0.0006
1987 0.01 29.23 29.222 0.0003
1988 0.01 33.72 33.71 0.0003
1989 0.02 55.5 55.485 0.0003
1990 0.07 110.93 110.86 0.0006
1991 0.11 217.12 217.01 0.0005
1992 0.12 194.43 194.31 0.0006
1993 0.11 211.99 211.88 0.0005
1994 0.31 516.2 515.89 0.0006
1995 0.64 735.97 735.33 0.0009
1996 0.72 1050.3 1049.6 0.0007
1997 1.02 1398.9 1397.9 0.0007
1998 1.09 1449.6 1448.5 0.0008
1999 1.11 1546.8 1545.7 0.0007
2000 1.39 1655.7 1654.3 0.0008
2001 1.62 2121.7 2120.1 0.0008
2002 2.16 2864.1 2861.9 0.0008
2003 4.09 4032.5 4028.4 0.001
2004 2.81 6099.3 6096.5 0.0005
2005 12.3 8188.7 8176.4 0.0015
2006 7.54 10663 10656 0.0007
2007 22283
So K = 2 is the best choice of cointegration equation
and error correction model with the limit of sample ca-
pacity, gets the VEC model as follows,
4.2.2. VEC Model Estimation Results of Equilibrium
Foreign Exchange Re serves Demand Based on
Chinese data between 1985 and 2006
4.2.2.1. Delay section K = 1
D(LNR) = –0.02082643444*( LNR(–1)
– 0.81557953*LNSX(–1) – 0.91636494*LNM(–1)
+ 0.71058393*LNI(–1) – 0.04742 8193*LNG(–1)
– 0.3588416363 ) + 0.25008865*D(LNR(–1))
+ 0.1427340478*D (LNSX(–1))
+ 0.02230181302*D(LNM(–1))
– 0.06450460302*D (LNI(–1))
– 0.02126208418*D(LNG(–1)) + 0.1450919242
D(LNSX) = 0.03164245422*( LNR(–1)
– 0.815579531*LNSX(–1) – 0.9163649488*LNM( –1)
+ 0.710583936*LNI(–1) – 0.0474281939*LNG(–1)
– 0.358841636 ) – 0.20362 37*D(LNR(–1))
– 0.64870222*D(LNSX(–1))
+ 0.0517247267*D (LNM(–1))
+ 0.5572220392*D(LNI(–1))
– 0.02544716867*D(LNG(–1)) + 0.15891 21152
D(LNM) = 1.220107884*( LNR(–1)
– 0.8155795318*LNSX(–1) – 0.9163649488*LNM(–1)
+ 0.710583936*LNI(–1) – 0.0474281939* LNG(–1)
– 0.358841636) + 0. 888630 89*D(LNR(–1))
– 0.9519198157*D(LNSX(– 1))
– 0.008114850993*D(LNM(–1))
+ 0.2931732124*D (LNI(–1))
+ 0.04427418309*D(LNG(–1)) – 0.1860917443
D(LNI) = –0.3332935656*( LNR(–1)
– 0.81557953*LNSX(–1) – 0.9163649488*LNM(–1)
+ 0.710583936*LNI(–1) – 0.047428193*LNG(–1)
– 0.358841636 ) + 0.0313 8545*D (LNR(–1))
– 0.6885940951*D (LNSX(–1))

S. H. ZENG 364
– 0.07677391686*D (LNM(–1))
+ 0.7975711815*D (LNI(–1))
– 0.08023819174*D (LNG(–1)) + 0.07411662228
D(LNG) = 2.164457793*( LNR(–1)
– 0.8155795318*LNSX(–1) – 0.9163649488*LNM(–1)
+ 0.710583936*LNI(–1) – 0.0474281939*LNG(–1)
– 0.35884163 ) – 0.64807905*D(LNR(–1))
– 2.3799935*D(LNSX(–1))
+ 0.7679206802*D(LNM(–1))
+ 0.8411639391*D (LNI(–1))
– 0.3874419347*D (LNG(–1)) + 0.7787188403
The long term equilibrium relation of these variables
LNR, LNSX, LNM, LNI, LN are,
LNR (–1) = 0.8155 795318*LNSX (–1)
+ 0.9163649488*LNM (–1) – 0.7105839363*LNI (–1)
+ 0.04742819394*LNG (–1) + 0.3588416 363
4.2.2.2. Delay Section K = 2
D(LNR) = 0.0210919311*( LNR (–1)
– 8.39646148*LNSX(–1) – 6.53172328* LNM(–1)
+ 9.319611202*LNI(–1) + 5.92161891 5*LNG(–1)
+ 72.52744886 ) – 0.4199163 335*D (LNR(–1))
+ 0.02744055717*D(LNR(–2))
+ 0.178363838*D (LNSX(–1))
– 0.07798941*D(LNSX(–2)) + 0.1637*D(LNM(–1))
+ 0.100098*D(LNM(–2)) – 0.210331*D(LNI(–1))
+ 0.043212*D(LNI(–2)) – 0.13208757*D(LNG(–1))
– 0.07503047391*D (LNG(–2)) + 0.3559304786
D(LNSX) = 0.0099460 85465*( LNR(–1 )
– 8.396461487*LNSX(–1) – 6.531723289*LNM(–1)
+ 9.3196112*LNI(– 1) + 5.92161891 5*LNG(–1)
+ 72.52744886 ) – 0.9757317399*D (LNR(–1))
+ 0.2452650037*D (LNR(–2))
+ 0.0633299*D(LNSX(–1)) + 0.622115*D(LNSX(–2))
+ 0.063976*D(LNM(–1)) + 0.03197 *D(LNM(–2))
+ 0.34938*D(LNI(–1)) – 0.55305 4*D(LNI(–2))
– 0.09832038718*D(LNG(–1))
– 0.0638524772*D (LNG(–2)) + 0.25181 44464
D(LNM) = –0.028990184*( LNR (–1)
– 8.396461487*LNSX(–1) – 6.531723289*LNM(–1)
+ 9.319611202*LNI(–1) + 5.921618915*LNG(–1)
+ 72.52744886 ) + 3.9950447*D(LNR(–1))
– 0.9449371943*D (LNR(–2))
+ 0.23898574*D(LNSX(–1))
+ 0.55443735*D (LNSX(–2)) – 1.12316*D(LNM(–1))
– 0.6771437*D(LNM(–2) )
+ 0.3818*D(LNI(–1)) – 0.830993*D(LNI(–2))
+ 0.2355717803*D (LNG(–1))
+ 0.09248289596*D(LNG(–2)) – 0.6183 532604
D(LNI) = – 0.01178074236*( LNR(– 1)
– 8.3964614*LNSX (–1) – 6.53172 3289*LNM(–1)
+ 9.319611202*LNI(–1) + 5.92161891*LNG(–1)
+ 72.5274488 ) – 0.1287365454*D(LNR(–1))
– 0.5332005646*D(LNR(–2 ))
– 0.04472733462*D (LNSX(–1))
+ 0.3249581422*D(LNSX(–2))
+ 0.0638542*D(LNM(–1) ) + 0.0026686*D(LNM(–2))
+ 0.852404135*D(LNI(–1)) – 0.72172054*D(LNI(–2))
– 0.052984839*D(LNG(–1))
+ 0.002247385*D (LNG(–2)) + 0.1702761775
D(LNG) = –0.3047102393*( LNR(–1)
– 8.396461487*LNSX(–1) – 6.53172 3289*LNM(–1)
+ 9.319611202*LNI(–1) + 5.92161891 5*LNG (–1)
+ 72.52744886) + 14.95319432*D(LNR(–1))
– 4.995081418*D(LNR(–2)) – 3.7942098*D(LNSX(–1))
+ 0.42273224*D(LNSX(–2)) – 1.7528*D(LNM(–1))
– 1.626889*D(LNM(–2)) + 2.911406* D(LNI(–1))
+ 0.211057*D(LNI(–2)) + 1.112724587*D(LNG(–1))
+ 0.8964220686*D(LNG(–2)) – 1.644163043
So the long term equilibrium relation of these vari-
ables LNR(–1), LNSX(–1), LNM(–1), LNI(–1), LNG(–1)
are
LNR(–1) = 8.39646148 7*LNSX(–1)
+ 6.531723289*LNM(–1) – 9.319611202*LNI(–1)
– 5.921618915*LNG(–1) – 72.52744886
The upper equation express that, the elasticity that the
Chinese foreign exchange reserves to export standard
deviation (SX) is 8.396461487, it means that the export
standard deviation increased 1%, the foreign exchange
reserves will increase 8.396461487%.The elasticity that
the Chinese foreign exchange reserves to the marginal
propensity to import (m) is 6.531723289, it means that
the marginal propensity to import increased 1%, the for-
eign exchange reserves will increase 6.531723289%.It
can be explained that, the marginal propensity to import
means the unit output increased will caused more import,
so more reserves are necessary for the need of import.
The elasticity of the Chinese foreign exchange re-
serves to the net opportunity cost (i)1 is –9.319611202, it
means that the net opportunity cost of hold foreign ex-
change reserves increased 1%; the Chinese foreign ex-
change reserves will reduce 9.319611202%.
The elasticity between the foreign exchange reserves
and the reaction coefficient of income to export is –
5.921618915, it means that the reaction coefficient of
income to export increased 1%, the foreign exchange
reserves will reduce 5.921618915.
It can be explained that, the reaction coefficient of in-
come to export is g increased, means that the increased
unit export will lead to the unit output increase, and then
increased the export lead to the foreign exchange re-
1net opportunity cost = return rate of capital – return rate of Chinese
foreign exchange reserves.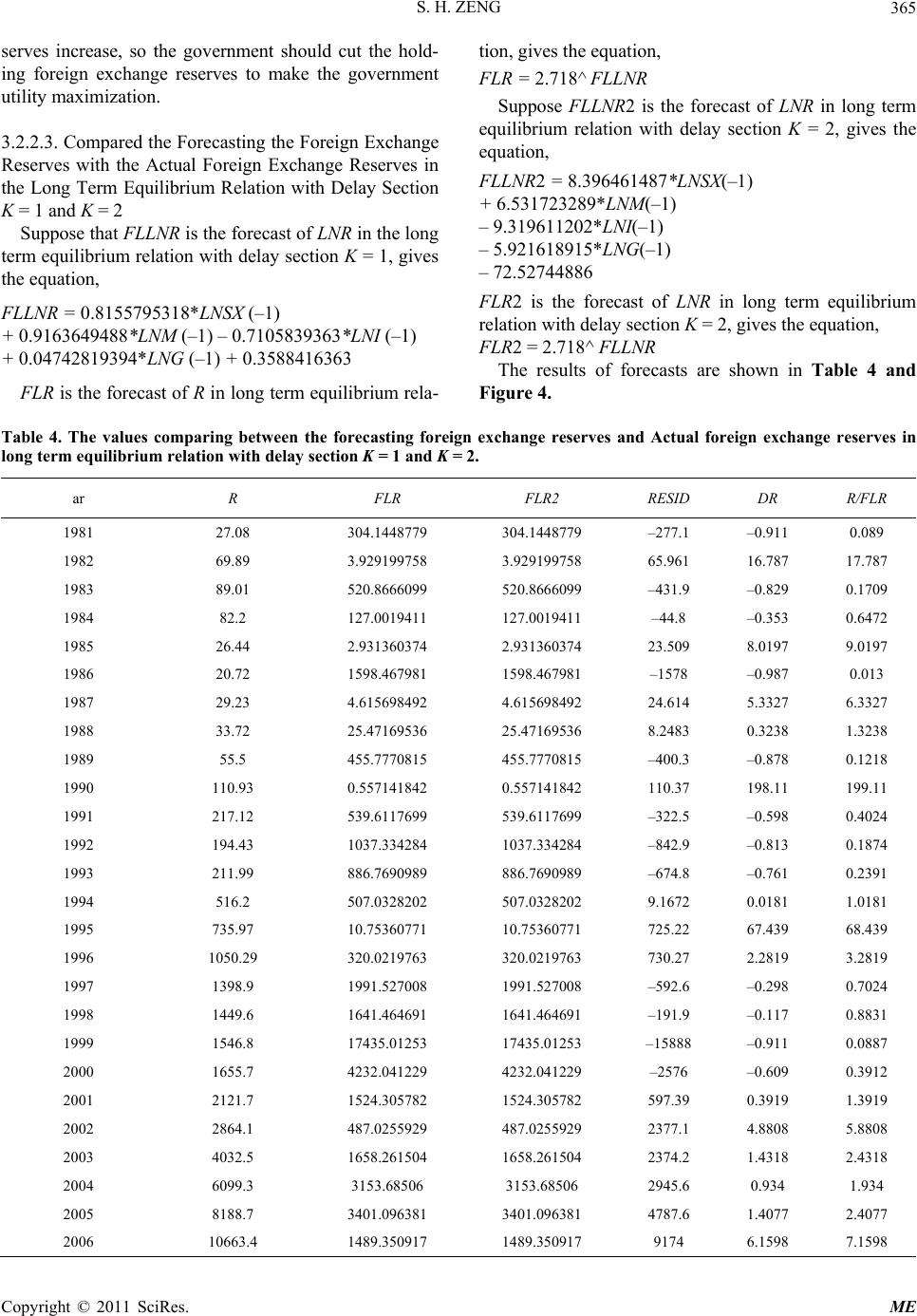

S. H. ZENG 365
serves increase, so the government should cut the hold-
ing foreign exchange reserves to make the government
utility maximization.
3.2.2.3. Compared the Forecasting the Foreign Exchange
Reserves with the Actual Foreign Exchange Reserves in
the Long Term Equilibrium Relation with Delay Section
K = 1 and K = 2
Suppose that FLLNR is the forecast of LNR in the long
term equilibrium relation with delay section K = 1, gives
the equation,
FLLNR = 0.815579531 8*LNSX (–1)
+ 0.9163649488*LNM (–1) – 0.7105 839363 *LNI (–1)
+ 0.04742819394* LNG (–1 ) + 0.3588 41636 3
FLR is the forecast of R in long term equilibrium rela-
tion, gives the equation,
FLR = 2.718^ FLLNR
Suppose FLLNR2 is the forecast of LNR in long term
equilibrium relation with delay section K = 2, gives the
equation,
FLLNR2 = 8.396461487*LNSX(–1)
+ 6.531723289*LNM(–1)
– 9.319611202*LNI(–1)
– 5.921618915*LNG(–1)
– 72.52744886
FLR2 is the forecast of LNR in long term equilibrium
relation with delay section K = 2, gives the equation,
FLR2 = 2.718^ FLLNR
The results of forecasts are shown in Table 4 and
Figure 4.
Table 4. The values comparing between the forecasting foreign exchange reserves and Actual foreign exchange reserves in
long term equilibrium relation with delay section K = 1 and K = 2.
ar R FLR FLR2 RESID DR R/FLR
1981 27.08 304.1448779 304.1448779 –277.1 –0.911 0.089
1982 69.89 3.929199758 3.929199758 65.961 16.787 17.787
1983 89.01 520.8666099 520.8666099 –431.9 –0.829 0.1709
1984 82.2 127.0019411 127.0019411 –44.8 –0.353 0.6472
1985 26.44 2.931360374 2.931360374 23.509 8.0197 9.0197
1986 20.72 1598.467981 1598.467981 –1578 –0.987 0.013
1987 29.23 4.615698492 4.615698492 24.614 5.3327 6.3327
1988 33.72 25.47169536 25.47169536 8.2483 0.3238 1.3238
1989 55.5 455.7770815 455.7770815 –400.3 –0.878 0.1218
1990 110.93 0.557141842 0.557141842 110.37 198.11 199.11
1991 217.12 539.6117699 539.6117699 –322.5 –0.598 0.4024
1992 194.43 1037.334284 1037.334284 –842.9 –0.813 0.1874
1993 211.99 886.7690989 886.7690989 –674.8 –0.761 0.2391
1994 516.2 507.0328202 507.0328202 9.1672 0.0181 1.0181
1995 735.97 10.75360771 10.75360771 725.22 67.439 68.439
1996 1050.29 320.0219763 320.0219763 730.27 2.2819 3.2819
1997 1398.9 1991.527008 1991.527008 –592.6 –0.298 0.7024
1998 1449.6 1641.464691 1641.464691 –191.9 –0.117 0.8831
1999 1546.8 17435.01253 17435.01253 –15888 –0.911 0.0887
2000 1655.7 4232.041229 4232.041229 –2576 –0.609 0.3912
2001 2121.7 1524.305782 1524.305782 597.39 0.3919 1.3919
2002 2864.1 487.0255929 487.0255929 2377.1 4.8808 5.8808
2003 4032.5 1658.261504 1658.261504 2374.2 1.4318 2.4318
2004 6099.3 3153.68506 3153.68506 2945.6 0.934 1.934
2005 8188.7 3401.096381 3401.096381 4787.6 1.4077 2.4077
2006 10663.4 1489.350917 1489.350917 9174 6.1598 7.1598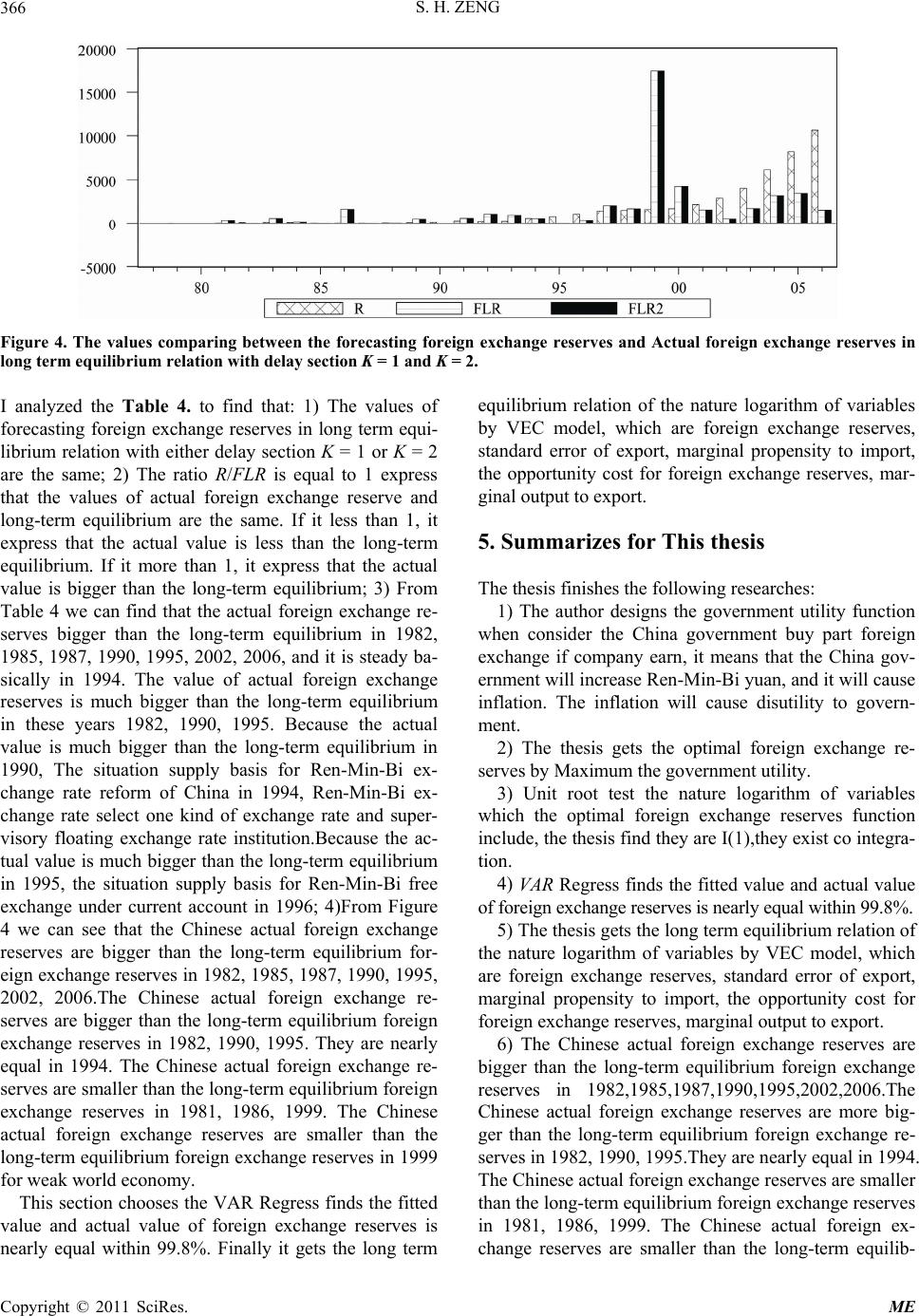

S. H. ZENG 366
Figure 4. The values comparing between the forecasting foreign exchange reserves and Actual foreign exchange reserves in
long term equilibrium relation with delay section K = 1 and K = 2.
I analyzed the Table 4. to find that: 1) The values of
forecasting foreign exchange reserves in long term equi-
librium relation with either delay section K = 1 or K = 2
are the same; 2) The ratio R/FLR is equal to 1 express
that the values of actual foreign exchange reserve and
long-term equilibrium are the same. If it less than 1, it
express that the actual value is less than the long-term
equilibrium. If it more than 1, it express that the actual
value is bigger than the long-term equilibrium; 3) From
Table 4 we can find that the actual foreign exchange re-
serves bigger than the long-term equilibrium in 1982,
1985, 1987, 1990, 1995, 2002, 2006, and it is steady ba-
sically in 1994. The value of actual foreign exchange
reserves is much bigger than the long-term equilibrium
in these years 1982, 1990, 1995. Because the actual
value is much bigger than the long-term equilibrium in
1990, The situation supply basis for Ren-Min-Bi ex-
change rate reform of China in 1994, Ren-Min-Bi ex-
change rate select one kind of exchange rate and super-
visory floating exchange rate institution.Because the ac-
tual value is much bigger than the long-term equilibrium
in 1995, the situation supply basis for Ren-Min-Bi free
exchange under current account in 1996; 4)From Figure
4 we can see that the Chinese actual foreign exchange
reserves are bigger than the long-term equilibrium for-
eign exchange reserves in 1982, 1985, 1987, 1990, 1995,
2002, 2006.The Chinese actual foreign exchange re-
serves are bigger than the long-term equilibrium foreign
exchange reserves in 1982, 1990, 1995. They are nearly
equal in 1994. The Chinese actual foreign exchange re-
serves are smaller than the long-term equilibrium foreign
exchange reserves in 1981, 1986, 1999. The Chinese
actual foreign exchange reserves are smaller than the
long-term equilibrium foreign exchange reserves in 1999
for weak world economy.
This section chooses the VAR Regress finds the fitted
value and actual value of foreign exchange reserves is
nearly equal within 99.8%. Finally it gets the long term
equilibrium relation of the nature logarithm of variables
by VEC model, which are foreign exchange reserves,
standard error of export, marginal propensity to import,
the opportunity cost for foreign exchange reserves, mar-
ginal output to export.
5. Summarizes for This thesis
The thesis finishes the following researches:
1) The author designs the government utility function
when consider the China government buy part foreign
exchange if company earn, it means that the China gov-
ernment will increase Ren-Min-Bi yuan, and it will cause
inflation. The inflation will cause disutility to govern-
ment.
2) The thesis gets the optimal foreign exchange re-
serves by Maximum the government utility.
3) Unit root test the nature logarithm of variables
which the optimal foreign exchange reserves function
include, the thesis find they are I(1),they exist co integra-
tion.
4) VAR Regress finds the fitted value and actual value
of foreign exchange reserves is nearly equal within 99.8%.
5) The thesis gets the long term equilibrium relation of
the nature logarithm of variables by VEC model, which
are foreign exchange reserves, standard error of export,
marginal propensity to import, the opportunity cost for
foreign exchange reserves, marginal output to export.
6) The Chinese actual foreign exchange reserves are
bigger than the long-term equilibrium foreign exchange
reserves in 1982,1985,1987,1990,1995,2002,2006.The
Chinese actual foreign exchange reserves are more big-
ger than the long-term equilibrium foreign exchange re-
serves in 1982, 1990, 1995.They are nearly equal in 1994.
The Chinese actual foreign exchange reserves are smaller
than the long-term equilibrium foreign exchange reserves
in 1981, 1986, 1999. The Chinese actual foreign ex-
change reserves are smaller than the long-term equilib-

S. H. ZENG367
rium foreign exchange reserves in 1999 for weak world
economy.
Different from the Kelly, Michael G. (1970) [3], Kelly,
Michael G. (1970) designed the government utility func-
tion without considering the China government buy part
foreign exchange if company earn, it means that the
China government will increase Ren-Min-Bi yuan, and it
will cause inflation. The inflation will cause disutility to
government. Finally it gets the optimal fuction, we can
find through the sample data about 46 countries from
1953 to 1965, (1) the government-holding foreign ex-
change reserves has positive correlation with the export
standard error, (2) it has positive correlation with the
average propensity to import [3].
This thesis designed the government utility function
when consider the China government buy part foreign
exchange if company earn, it means that the China gov-
ernment will increase Ren-Min-Bi yuan, and it will cause
inflation. The inflation will cause disutility to govern-
ment. Finally it gets the optimal fuction, using the sam-
ple datas in China 1980-2006 and VEC we can find: 1)
The government-holding foreign exchange reserves has
positive correlation with the export standard error; 2) It
has positive correlation with the marginal propensity to
import. The optimal fuction, data and regression method
are all different, but all have the positive correlation be-
tween the foreign exchange reserves and export standard
error, also is consonant with the results about the mar-
ginal propensity to import basically.
Different from Guobo Huang (1995), Guobo Huang
(1995) collected the correlative economic datas from
1980 to 1990 in China, using ECM based on the quar-
terly datas to research the international reserves scale and
discovered that: 1) The Chinese foreign exchange reserve
has the negative correlation with import, that is when the
import increased the foreign exchange reserves will re-
duce; 2) it has negative correlation with average propen-
sity to import, that is when the average propensity to
import increased the foreign exchange reserves will re-
duce. The thesis find that the elasticity that the Chinese
foreign exchange reserves to the marginal propensity to
import (m) is 6.531723289, it means that the marginal
propensity to import increased 1%, the foreign exchange
reserves will increase 6.531723289%.It can be explained
that, the marginal propensity to import means the unit
output increased will caused more import, so more re-
serves are necessary for the need of import.
6. Acknowledgements
I would like to thank reviewer for their opinions, and
thank proffessor Yuding Yu.
7. References
[1] H. R. Heller, “Optimal International Reserves,” The
Economic Journal, Vol. 76, No. 302, 1966, pp. 296-308.
[2] P. B. Clark, “Optimum International Reserves and the
Speed of Adjustment,” Journal of Political Economy, Vol.
78, No. 2, pp. 356-376.
[3] M. G. Kelly, “The Demand for International Reserves,”
American Economic Review, Vol. 60, No. 4, pp. 655-667.
[4] G. B. Huang, “Modeling China’s Demand for Interna-
tional Reserves,” Applied Financial Economics, Vol. 5,
No. 5, pp. 357-366. doi:10.1080/758522763
[5] Y. D. Yu, “Some Problems on Foreign Exchange Re-
serves and International Balances,” World Economics and
Polics, No. 10, 1997, pp.18-23.
[6] J. Wu, “The Analysis and Affirmation of the China For-
eign Exchange Reserves,” Economy Research Journal,
Vol. 33, No. 6, 1998, pp. 20-29.
[7] C. M. Xu, “The Reality of the Demand of the Foreign
Exchange Reserves in China,” Quantitative and Techni-
cal Economics, 2001, No. 12, pp. 101-103.
[8] M. Victoria, “Getting out from between a Rock and a
Hard Place: Can China Use Its Foreign Exchange Re-
serves to Save Its Banks?” Journal of International Fi-
nancial Markets, Institutions and Money, Vol. 16, No. 4,
2006, pp. 345-354.
[9] M. Ramachandran, “On the Upsurge of Foreign Ex-
change Reserves in India,” Journal of Policy Modeling,
Vol. 28, No. 7, 2006, pp. 797-809.
doi:10.1016/j.jpolmod.2006.04.006
[10] K. Adnan and D. Ayhan, “Foreign Exchange Reserves
and Exchange Rates in Turkey: Structural Breaks, Unit
Roots and Cointegration,” Economic Modelling, Vol. 25,
No. 1, 2008, pp. 83-92.
[11] V. Pontines and R. S. Rajan, “Foreign Exchange Market
Intervention and Reserve Accumulation in Emerging
Asia: Is there Evidence of Fear of Appreciation?” Eco-
nomics Letters, Vol. 111, No. 3, 2011, pp. 252- 255.
doi:10.1016/j.econmod.2007.04.010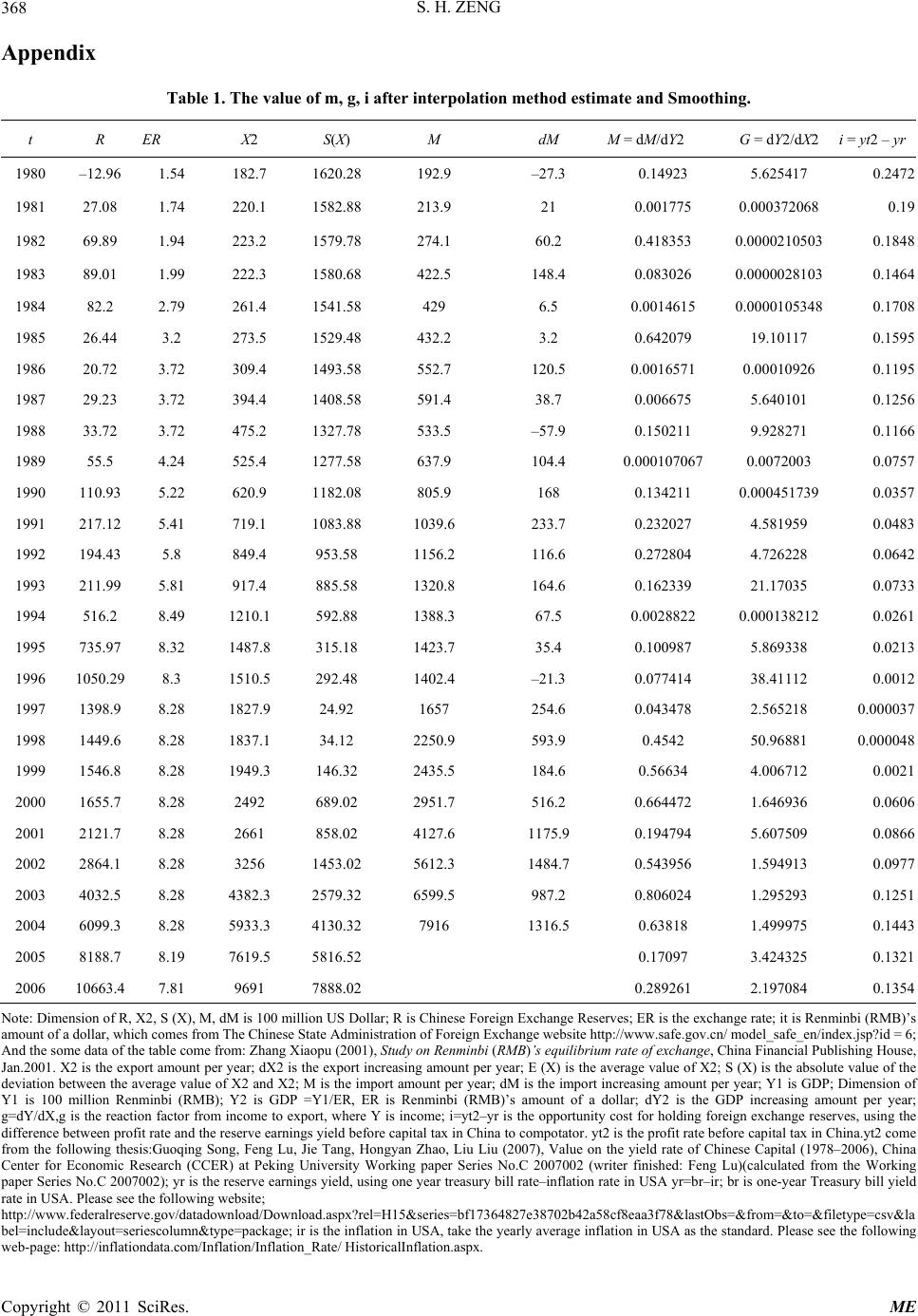

S. H. ZENG 368
Appendix
Table 1. The value of m, g, i after interpolation method estimate and Smoothing.
t R ER X2 S(X) M dM M = dM/dY2 G = dY2/dX2 i = yt2 – yr
1980 –12.96 1.54 182.7 1620.28 192.9 –27.3 0.14923 5.625417 0.2472
1981 27.08 1.74 220.1 1582.88 213.9 21 0.001775 0.000372068 0.19
1982 69.89 1.94 223.2 1579.78 274.1 60.2 0.418353 0.0000210503 0.1848
1983 89.01 1.99 222.3 1580.68 422.5 148.4 0.083026 0.0000028103 0.1464
1984 82.2 2.79 261.4 1541.58 429 6.5 0.0014615 0.0000105348 0.1708
1985 26.44 3.2 273.5 1529.48 432.2 3.2 0.642079 19.10117 0.1595
1986 20.72 3.72 309.4 1493.58 552.7 120.5 0.0016571 0.00010926 0.1195
1987 29.23 3.72 394.4 1408.58 591.4 38.7 0.006675 5.640101 0.1256
1988 33.72 3.72 475.2 1327.78 533.5 –57.9 0.150211 9.928271 0.1166
1989 55.5 4.24 525.4 1277.58 637.9 104.4 0.000107067 0.0072003 0.0757
1990 110.93 5.22 620.9 1182.08 805.9 168 0.134211 0.000451739 0.0357
1991 217.12 5.41 719.1 1083.88 1039.6 233.7 0.232027 4.581959 0.0483
1992 194.43 5.8 849.4 953.58 1156.2 116.6 0.272804 4.726228 0.0642
1993 211.99 5.81 917.4 885.58 1320.8 164.6 0.162339 21.17035 0.0733
1994 516.2 8.49 1210.1 592.88 1388.3 67.5 0.0028822 0.000138212 0.0261
1995 735.97 8.32 1487.8 315.18 1423.7 35.4 0.100987 5.869338 0.0213
1996 1050.29 8.3 1510.5 292.48 1402.4 –21.3 0.077414 38.41112 0.0012
1997 1398.9 8.28 1827.9 24.92 1657 254.6 0.043478 2.565218 0.000037
1998 1449.6 8.28 1837.1 34.12 2250.9 593.9 0.4542 50.96881 0.000048
1999 1546.8 8.28 1949.3 146.32 2435.5 184.6 0.56634 4.006712 0.0021
2000 1655.7 8.28 2492 689.02 2951.7 516.2 0.664472 1.646936 0.0606
2001 2121.7 8.28 2661 858.02 4127.6 1175.9 0.194794 5.607509 0.0866
2002 2864.1 8.28 3256 1453.02 5612.3 1484.7 0.543956 1.594913 0.0977
2003 4032.5 8.28 4382.3 2579.32 6599.5 987.2 0.806024 1.295293 0.1251
2004 6099.3 8.28 5933.3 4130.32 7916 1316.5 0.63818 1.499975 0.1443
2005 8188.7 8.19 7619.5 5816.52 0.17097 3.424325 0.1321
2006 10663.4 7.81 9691 7888.02 0.289261 2.197084 0.1354
Note: Dimension of R, X2, S (X), M, dM is 100 million US Dollar; R is Chinese Foreign Exchange Reserves; ER is the exchange rate; it is Renminbi (RMB)’s
amount of a dollar, which comes from The Chinese State Administration of Foreign Exchange website http://www.safe.gov.cn/ model_safe_en/index.jsp?id = 6;
And the some data of the table come from: Zhang Xiaopu (2001), Study on Renminbi (RMB)’s equilibrium rate of exchange, China Financial Publishing House,
Jan.2001. X2 is the export amount per year; dX2 is the export increasing amount per year; E (X) is the average value of X2; S (X) is the absolute value of the
deviation between the average value of X2 and X2; M is the import amount per year; dM is the import increasing amount per year; Y1 is GDP; Dimension of
Y1 is 100 million Renminbi (RMB); Y2 is GDP =Y1/ER, ER is Renminbi (RMB)’s amount of a dollar; dY2 is the GDP increasing amount per year;
g=dY/dX,g is the reaction factor from income to export, where Y is income; i=yt2–yr is the opportunity cost for holding foreign exchange reserves, using the
difference between profit rate and the reserve earnings yield before capital tax in China to compotator. yt2 is the profit rate before capital tax in China.yt2 come
from the following thesis:Guoqing Song, Feng Lu, Jie Tang, Hongyan Zhao, Liu Liu (2007), Value on the yield rate of Chinese Capital (1978–2006), China
Center for Economic Research (CCER) at Peking University Working paper Series No.C 2007002 (writer finished: Feng Lu)(calculated from the Working
paper Series No.C 2007002); yr is the reserve earnings yield, using one year treasury bill rate–inflation rate in USA yr=br–ir; br is one-year Treasury bill yield
rate in USA. Please see the following website;
http://www.federalreserve.gov/datadownload/Download.aspx?rel=H15&series=bf17364827e38702b42a58cf8eaa3f78&lastObs=&from=&to=&filetype=csv&la
bel=include&layout=seriescolumn&type=package; ir is the inflation in USA, take the yearly average inflation in USA as the standard. Please see the following
web-page: http://inflationdata.com/Inflation/Inflation_Rate/ HistoricalInflation.aspx.

S. H. ZENG369
Table 2. The actual value of M, Y2, yt2, br, ir, yr = br – ir, i = yt2 – yr.
t Y1 Y2 dY2 M = dM/dY2 g = dY2/dX yt2 br ir yr i
1980 4517.8 2933.636 259.3317 0.14923 5.625417 25.00%13.86% 13.58% 0.28%0.2472
1981 4862.4 2794.483 –139.154 –0.1775 –3.72068 22.00%13.35% 10.35% 3.00%0.19
1982 5294.7 2729.227 –65.256 0.418353 –21.0503 21.00%8.68% 6.16% 2.52%0.1848
1983 5934.5 2982.161 252.934 0.083026 –281.038 21.50%10.08% 3.22% 6.86%0.1464
1984 7171 2570.251 –411.91 –0.14615 –10.5348 22.00%9.22% 4.30% 4.92%0.1708
1985 8964.4 2801.375 231.1241 0.642079 19.10117 20.00%7.60% 3.55% 4.05%0.1595
1986 10275.2 2762.151 –39.2245 –0.16571 –1.0926 16.00%5.95% 1.90% 4.05%0.1195
1987 12058.6 3241.559 479.4086 0.006675 5.640101 16.00%7.10% 3.66% 3.44%0.1256
1988 15042.8 4043.763 802.2043 0.150211 9.928271 16.60%9.02% 4.08% 4.94%0.1166
1989 16992.3 4007.618 –36.1455 –1.07067 –0.72003 10.50%7.76% 4.83% 2.93%0.0757
1990 18667.8 3576.207 –431.411 0.134211 –4.51739 5.00% 6.82% 5.39% 1.43%0.0357
1991 21781.5 4026.155 449.9484 0.232027 4.581959 4.70% 4.12% 4.25% –0.13%0.0483
1992 26923.5 4641.983 615.8275 0.272804 4.726228 7.00% 3.61% 3.03% 0.58%0.0642
1993 35333.9 6081.566 1439.584 0.162339 21.17035 8.00% 3.63% 2.96% 0.67%0.0733
1994 48197.9 5677.02 –404.546 –0.28822 –1.38212 7.20% 7.20% 2.61% 4.59%0.0261
1995 60793.7 7306.935 1629.915 0.100987 5.869338 4.50% 5.18% 2.81% 2.37%0.0213
1996 67884.6 8178.867 871.9324 0.077414 38.41112 2.70% 5.51% 2.93% 2.58%0.0012
1997 74462.6 8993.068 814.2002 0.043478 2.565218 2.80% 5.51% 2.34% 3.17%–0.0037
1998 78345.2 9461.981 468.913 –0.04542 50.96881 2.50% 4.53% 1.55% 2.98%–0.0048
1999 82067.5 9911.534 449.5531 0.56634 4.006712 4.00% 5.98% 2.19% 3.79%0.0021
2000 89468.1 10805.33 893.7923 0.664472 1.646936 8.00% 5.32% 3.38% 1.94%0.0606
2001 97314.8 11753 947.6691 0.194794 5.607509 8.00% 2.17% 2.83% –0.66%0.0866
2002 105172.3 12701.97 948.9734 0.543956 1.594913 9.50% 1.32% 1.59% –0.27%0.0977
2003 117251.9 14160.86 1458.889 0.806024 1.295293 11.50%1.26% 2.27% –1.01%0.1251
2004 136515 16487.32 2326.461 0.63818 1.499975 14.50%2.75% 2.68% 0.07%0.1443
2005 182321 22261.42 5774.098 0.17097 3.424325 15.20%4.38% 2.39% 1.99%0.1321
2006 209407 26812.68 4551.26 0.289261 2.197084 15.30%5% 3.24% 1.76%0.1354
Note: 1. Y2 is GDP =Y1/ER, ER is Renminbi (RMB)’s amount of a dollar, ER come from Appendix Table 1; The meaning of Symbol Y1,dY2 and so on are
the same from Appendix Table 1; Dimension of Y1 is 100 million Renminbi (RMB), Dimension of Y2,DY2 is 100 million US Dollar.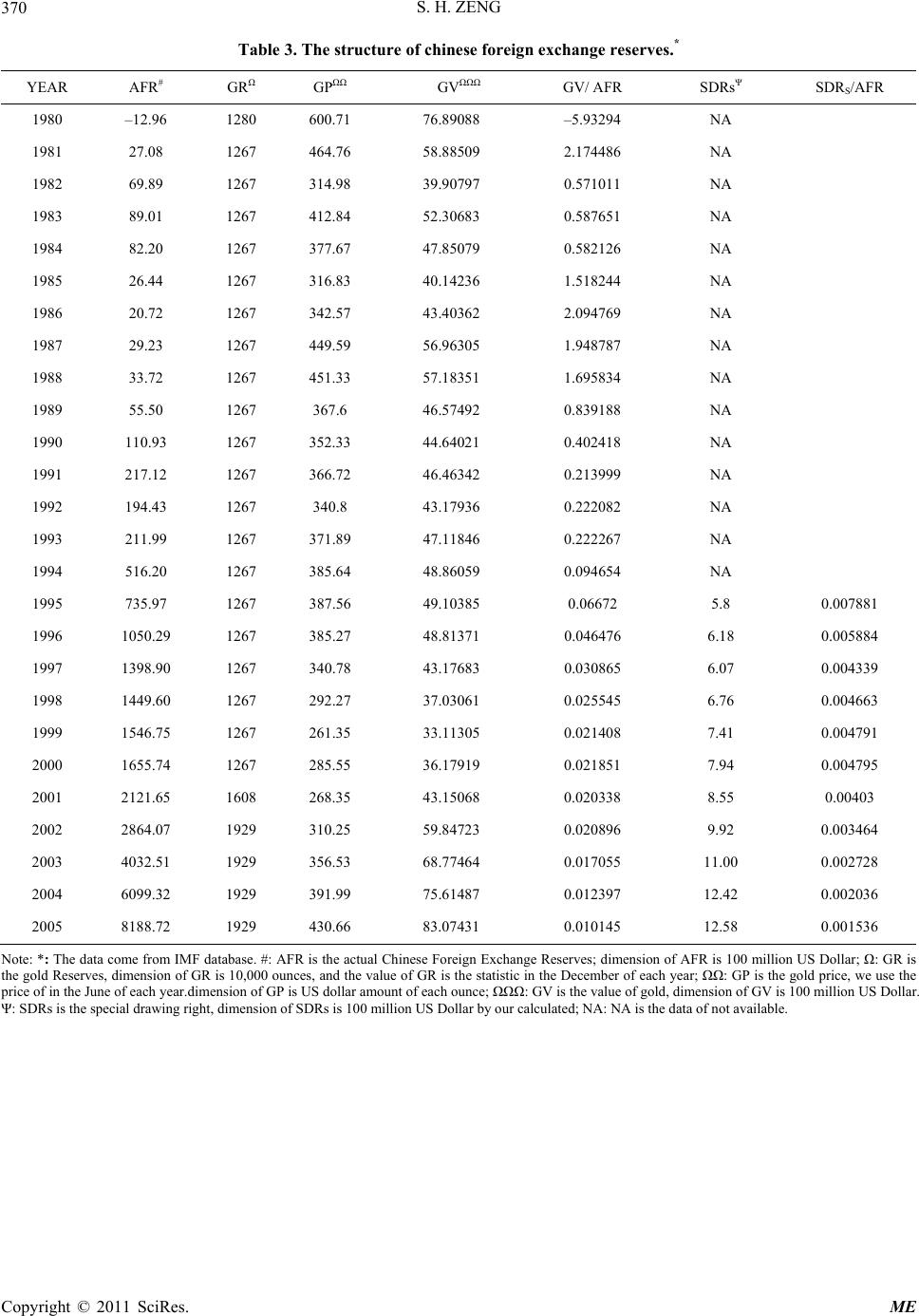

S. H. ZENG 370
Table 3. The structure of chinese foreign exchange reserves.*
YEAR AFR# GRΩ GPΩΩ GVΩΩΩ GV/ AFR SDRsΨ SDRS/AFR
1980 –12.96 1280 600.71 76.89088 –5.93294 NA
1981 27.08 1267 464.76 58.88509 2.174486 NA
1982 69.89 1267 314.98 39.90797 0.571011 NA
1983 89.01 1267 412.84 52.30683 0.587651 NA
1984 82.20 1267 377.67 47.85079 0.582126 NA
1985 26.44 1267 316.83 40.14236 1.518244 NA
1986 20.72 1267 342.57 43.40362 2.094769 NA
1987 29.23 1267 449.59 56.96305 1.948787 NA
1988 33.72 1267 451.33 57.18351 1.695834 NA
1989 55.50 1267 367.6 46.57492 0.839188 NA
1990 110.93 1267 352.33 44.64021 0.402418 NA
1991 217.12 1267 366.72 46.46342 0.213999 NA
1992 194.43 1267 340.8 43.17936 0.222082 NA
1993 211.99 1267 371.89 47.11846 0.222267 NA
1994 516.20 1267 385.64 48.86059 0.094654 NA
1995 735.97 1267 387.56 49.10385 0.06672 5.8 0.007881
1996 1050.29 1267 385.27 48.81371 0.046476 6.18 0.005884
1997 1398.90 1267 340.78 43.17683 0.030865 6.07 0.004339
1998 1449.60 1267 292.27 37.03061 0.025545 6.76 0.004663
1999 1546.75 1267 261.35 33.11305 0.021408 7.41 0.004791
2000 1655.74 1267 285.55 36.17919 0.021851 7.94 0.004795
2001 2121.65 1608 268.35 43.15068 0.020338 8.55 0.00403
2002 2864.07 1929 310.25 59.84723 0.020896 9.92 0.003464
2003 4032.51 1929 356.53 68.77464 0.017055 11.00 0.002728
2004 6099.32 1929 391.99 75.61487 0.012397 12.42 0.002036
2005 8188.72 1929 430.66 83.07431 0.010145 12.58 0.001536
Note: *: The data come from IMF database. #: AFR is the actual Chinese Foreign Exchange Reserves; dimension of AFR is 100 million US Dollar; Ω: GR is
the gold Reserves, dimension of GR is 10,000 ounces, and the value of GR is the statistic in the December of each year; ΩΩ: GP is the gold price, we use the
price of in the June of each year.dimension of GP is US dollar amount of each ounce; ΩΩΩ: GV is the value of gold, dimension of GV is 100 million US Dollar.
Ψ: SDRs is the special drawing right, dimension of SDRs is 100 million US Dollar by our calculated; NA: NA is the data of not available.