Paper Menu >>
Journal Menu >>
 American Journal of Computational Mathematics, 2011, 1, 39-54 doi:10.4236/ajcm.2011.12005 Published Online June 2011 (http://www.scirp.org/journal/ajcm) Copyright © 2011 SciRes. AJCM 39 Characteristic Analysis of Exponential Compact Higher Order Schemes for Convection-Diffusion Equations Sanyasiraju V. S. S. Yedida, Nachiketa Mishra Department of Mathematics, Indian Institute of Technology Madras, Chennai, India E-mail: sryedida@iitm.ac.in, mishra.nachiketa@gmail.com Received February 19, 201 1; revised March 23, 20 1 1; accepted April 5, 2011 Abstract This paper looks at the development of a class of Exponential Compact Higher Order (ECHO) schemes and attempts to comprehend their behaviour by introducing different combinations of discrete source function and its derivatives. The characteristic analysis is performed for one-dimensional schemes to understand the efficiency of the scheme and a similar analysis has been introduced for higher dimensional schemes. Finally, the developed schemes are used to solve several example problems and compared the error norms and rates of convergence. Keywords: Exponential Scheme, Compact Higher Order Scheme, Characteristics, Resolving Efficiency, Finite Difference 1. Introduction Many interesting engineering problems involve the physical processes and transport phenomena that include fluid flow, heat and mass transfer, can be modelled by a general Convection-Diffusion Equation (CDE). This equation describes the convection and diffusion chara- cteristics of various physical quantities, such as mome- ntum, energy, concentration, etc. This paper deals with the numerical solution of convection-diffusion equation of the form =(, ) xxyy xy aubucuduf x y (1) on , with boundary conditions 2 R (, )=(, )ux ygx y on , (2) where are constant diffusion, , are constant convection coefficients and , >0ab cd f , g are sufficiently smoo th functions with resp ect to x and . If , are very small when compared with and , then (1) becomes a convection dominated equation for which [1-4] are some of the exponential schemes known from the literature. For higher dim- ensional problems, though the schemes [2-4] are all fourth order accurate, scheme presented in [4] seems to be giving better results over the other two. The purpose of this work is to understand the good features of the scheme given in [4] and based on these features include some additional condition s in the development of ECHO schemes. Since the development of these schemes is already been discussed in [4], instead of repeating the same in this work, we focus on understanding the merits of the scheme. Section two presents a new class of ECHO schemes for 1D CDE, their classification and numerical verification. Echo schemes for 2D CDE are formulated and compared in the Section three and conclusions are drawn in the last section. y 0< a<<1b d c 2. 1D Convection-Diffusion Equations The one dimensional e q ui val ent of (1), by fixi ng , is given by ==0bd =() xx x aucuf x , , (3) 0< <1x with boundary conditions , , where 1 (0) =ug 2 (1) =ug 1 g , 2 g are some constants. 2.1. ECHO Schemes A general strategy to develop ECHO schemes is by starting with the difference equation 2= hihii Du cDuF (4) where 11 =( )/2 hi ii Du uuh and 21 =( 2 hi ii Du uu over a uniformly distributed nodal points with step length and 2 h hi 1)/ i u F is a linear combination of the source term i f and its derivatives at a chosen number  40 S.V.S.S. YEDIDA ET AL. of stencil (mesh) points with equal number of arbitrary constants (refer [2-4] for three such different choices). is taken to be coth 22 ch ch a when the convection coefficient so that the difference Equation (4) is exact for 0c cx a e otherwise it is equal to . If ai F is taken as i f then (4) is a second order compact exponential scheme which was discussed in [5]. In the development of the ECHO scheme, the arbitrary constants in i F are obtained by making the difference Equation (4) is exact for x , 2 x , In this work four different stencils are used for 3,x i F and the corresponding constants have been computed by forcing the difference scheme (4) to be at least fourth order accurate. The four chosen stencils and their constants are given by (refer [3,4] for the complete derivation of the computation of the coefficients). 2.1.1. Stencil-1 Consider the discrete source function 11ii23i1 4 =( i) ix F cfc f cfc f (5) where i f , () x i f are the source function and it’s derivative, respectively, at the nodal point . The i Equation (4) is already exact for 1, e 23 cx a 4 , and enforcing the exactness also for , , x xx 4 x gives four simultaneous equations in terms of its coefficients. Solving them for , gives i c=1 ,i, 2 3 & 32 1=0.25c2 1 630.5 3 , 2 22 =2 2 3 c , 32 2 3=0.25c1 630.5 3 0.5 32 6 , 4 ch=6 , =a ch , =ch for 0c and 11 =12 c, 25 =6 c, 31 12 13 c = c c ) , when . 4=0c=0 1 Similarly for the other stencils, system of equations are obtained and solved to get the corresponding co- efficients. 2.1.2. Stencil-2 12 =()()( i ixixi fcffc 0 4xi fFc (6) when the coefficients are c 1=1c, 32 11 .5 61 2 21 =0 0.5 212 ch , 32 325 =2 2 36 ch , 32 2 4111 =0.50 61212 ch .5 and , 1=1c2=24 h c , , 3=0c4=24 h c for c. =0 ) 2.1.3. Ste n ci l-3 12 34 =()()( iixixx ixxxi Fcfcf cfcf , (7) when 0c the coefficients are 1=1c, 2=( )ch , 22 31 =6 ch , 33 4=ch 2 11 612 , and , , 1=1c2=0c 2 3=12 h c, for . 4=0c=0c () i 2.1.4. Ste nc i l - 4 11 231 45 =() iiiixixx F cfc fcfcfcf (8) when 0c the coefficients are 43 2 1=123(14)(23 ) (0.5)(0.10.25) c , 432 2=24 244 20.8c 43 2 3=123(14 )(23 ) (0.5)(0.10.25) c , , 32 4=(660.5ch ) , 24 32 1 =1212 15 ch 5 , and 11 =30 c, 214 =15 c, 31 =30 c, , 4=0c 2 5=20 h c for . =0c Schemes with stencils 1, 2 and 3 contain four parameters and are fourth order accurate, whereas the scheme with stencil 4 contains five parameters and is sixth order accurate. Here after, we refer the difference scheme (4) with stencils 1 to 4 as schemes [1 ] 1 D S to [1 ] 4 D S, respectively for all the future references. Exponential schemes of [2,3] are also fourth order accurate with three arbitrary parameters and the scheme given in [4] uses six parameters to generate a sixth order scheme for the chosen one-dimensional convection- Copyright © 2011 SciRes. AJCM  S.V.S.S. YEDIDA ET AL. 41 diffusion equation. The discrete source terms of these schemes [2-4] ar e gi v en by. Stencil used in [2]: 11 = ii2 31ii F cfc fc f (9) 2 11 =0.50.5 6 c , 2 22 =2 2 3 c , 2 31 =0.50 6 c.5 when 0c , 11 =12 c, 25 =6 c, 31 =12 c when =0c. Stencil used in [3]: ) i12 =3 ()( iixixx F cfcfc f (10) c, ch 1=1 2=( ) , 22 31 =6 ch when , 0c 1=1c, 2=0c, 2 3=12 h c when =0c. Stencil used in [4]: 1 11 =2 31 4156 ()()() ii ii x ixix cfcf cfcf cf i (11) when the coefficients are Fcf 0c 54 90(1290)3 1=(7.512 ) 7 (0.5)0.375 30 c , 43 28 =2424 2 15 c , 54 3 3=90(1290 )(7.512 ) 7 (0.5)0.375 30 c , 54 3 42 306(15 )(3.56 ) =1 (0.5 )5 30 ch 5432 5= (12012082)ch , , 54 3 62 306(15 )(3.56 ) =1 (0.5 )5 30 ch , and 12 =15 c, 211 =15 c, 32 =15 c, 4=40 h c, 5=0c, 6=40 h c for =0c. Name the scheme (4) with stencils used in [2-4] as schemes [1 ] 5 D S, [1 ] 6 D S and [1] 7 D S, respectively. That is, a total ofn O sche have been introduced until now and out of which five of them are fourth order accurate and the other two are sixth order accurate. Among the fourth order schemes, three of them, developed in this work, have four free parameters and the other two, taken from the literature [2] and [3], have three parameters. Among the sixth order schemes, one scheme developed in this work has five free parameters and the other taken from the literature [1] 7 seveECHmes D S has six parameters. That is, the seven schemes canlassified into th n order schemes with n number of parameters and tther contain less than number of parameters. The aim of the rest of the works to demonstrate, using wave number analysis and numerical experimentation, the th n order ECHO schemes with n parameters are more accurate than the other class of scmes. be c ution he o 2.2. Com g th n i arison of the Characteristic Curves alys he , re p Usie wave number anissolof any n numerical scheme can be measured with which one can understand the closeness of the characteristic of a difference equation to that of the differential equ ation [6]. Since the stability of any numerical scheme depends on the magnitude of the peclet number, defined by =ch p, in this work, the characteristics are comparh respect to peclet numbers. The characteristic of the governing Equation (1), obtained by sub stituting a ed wit I wx e in the place of the dependent variable u, is given by: 2 c [1 ]= D I hp (12) wh ere =wh , is the nuwe wavmber, =1I . schemeSimilarha teristics of the differences are obtained by substituting ly, the crac I i e at i u to get (refer [4,6] for more details). Characteristic Cur[1D] 1 S ve for : '' 2 ' 1 z [1 ] 1= D hzI (13) wh cwIw ere w'=sin , ''=2 2wcos , 1 =coth 22 p , 14 31 =()sinz , 231 )co=( sz , 32 13 =p 11 0.250.5)) 3 6 ppp ((3 1 , 2 22 12 =2 2 , 3pp p 32 33 =p 11 0.251 3 6 ppp (3)( 0.5) , Copyright © 2011 SciRes. AJCM 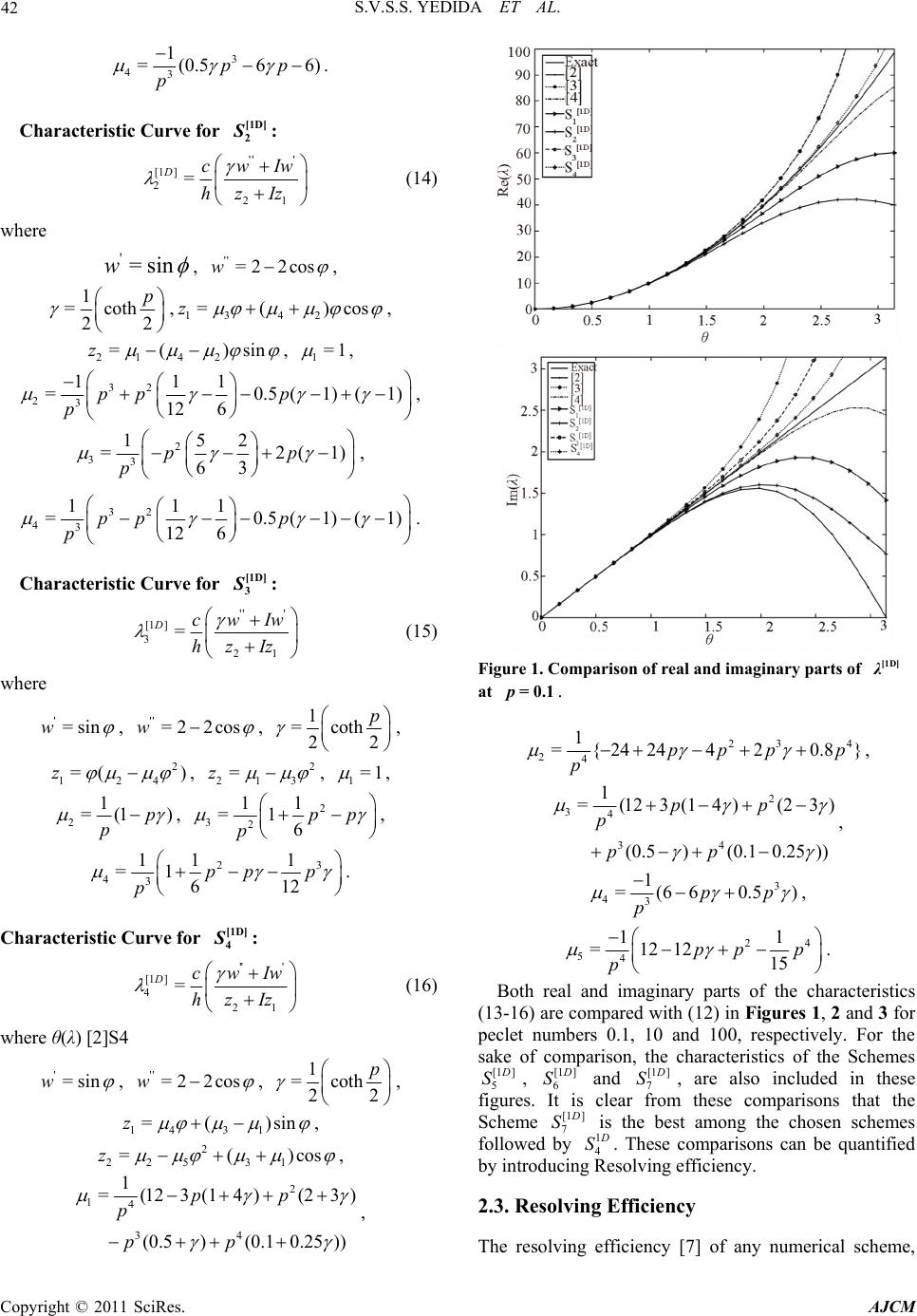 42 S.V.S.S. YEDIDA ET AL. 3 43 1 = (0.566)pp p teristic Curve for [1D] 2 . Charac S : '' ' [1 ] 2= D hz 21 cwIw zI (14) where sin= ' w, ''=2 2cosw , 1 )cosz=c oth 22 p ,1342 =( 2 )sin , 21 =(z4 , 1=1 , 32 231)1pp p , 111 =0 .5( 12 6p () 2 152 =2( 63 pp , 331) p 32 43 111 =0.5(1) 12 6 pp p p . Characteristic Curve for (1 ) [1D] 3 S : '' ' 21 cwIw I (15) where [1 ] 3= D hz z '=sinw , ''=2 2cosw , 1 =coth 22 p , 2 4 ) 12 =(z , 21 =z2 3 , 1=1 , 21 =(1 )p p , 2 32 11 =1 6pp p , 23 43 =1 p 111 61 pp p 2 . Characteristic Curve for [1D] 4 S : '' ' 21 cwIw (16) where θ(λ) [2]S4 [1 ] 4= D hz Iz '=sinw , ''=2 2cosw , 1 =coth 22 p , 14 1 ) 3 =(zsin 2 225 =( , 31 ) [1D] λ Figure 1. Comparison of real and imaginary parts of at =0.1p. 23 4 24 1 ={2424420.8}ppp p p , 2 cosz , 2 1) ( 1 0.25 pp 1 p4 34 =( 123(14 (0.5 )(0.pp 23 )) ) , 34 34 1 =(123(14)(23) (0.5)(0.10.25)) pp p pp , 3 43 1 =(66 0.5pp p) , 24 54 11 =121215 pp p p . Both real and imaginary parts of theharacteristics (13-16) are compared with (12) in Figures, 2 and 3 for peclet numbers 0.1, 10 and 100, respectively. For the sake of comparison, the characteristics of t Schemes c 1 he [1 ] 5 D S, [1 ] 6 D S and [1] 7 D S, are also included in these figures. It is clear from these comparisons that the Scheme [1 ] 7 D S is the best among the chosen schemes followed by 1 4 D S. These comparisons can be quantified by introducing Resolving efficiency. 2.3. Resolving Efficiency The resolvingficiency [7] of any numerical scheme, ef Copyright © 2011 SciRes. AJCM 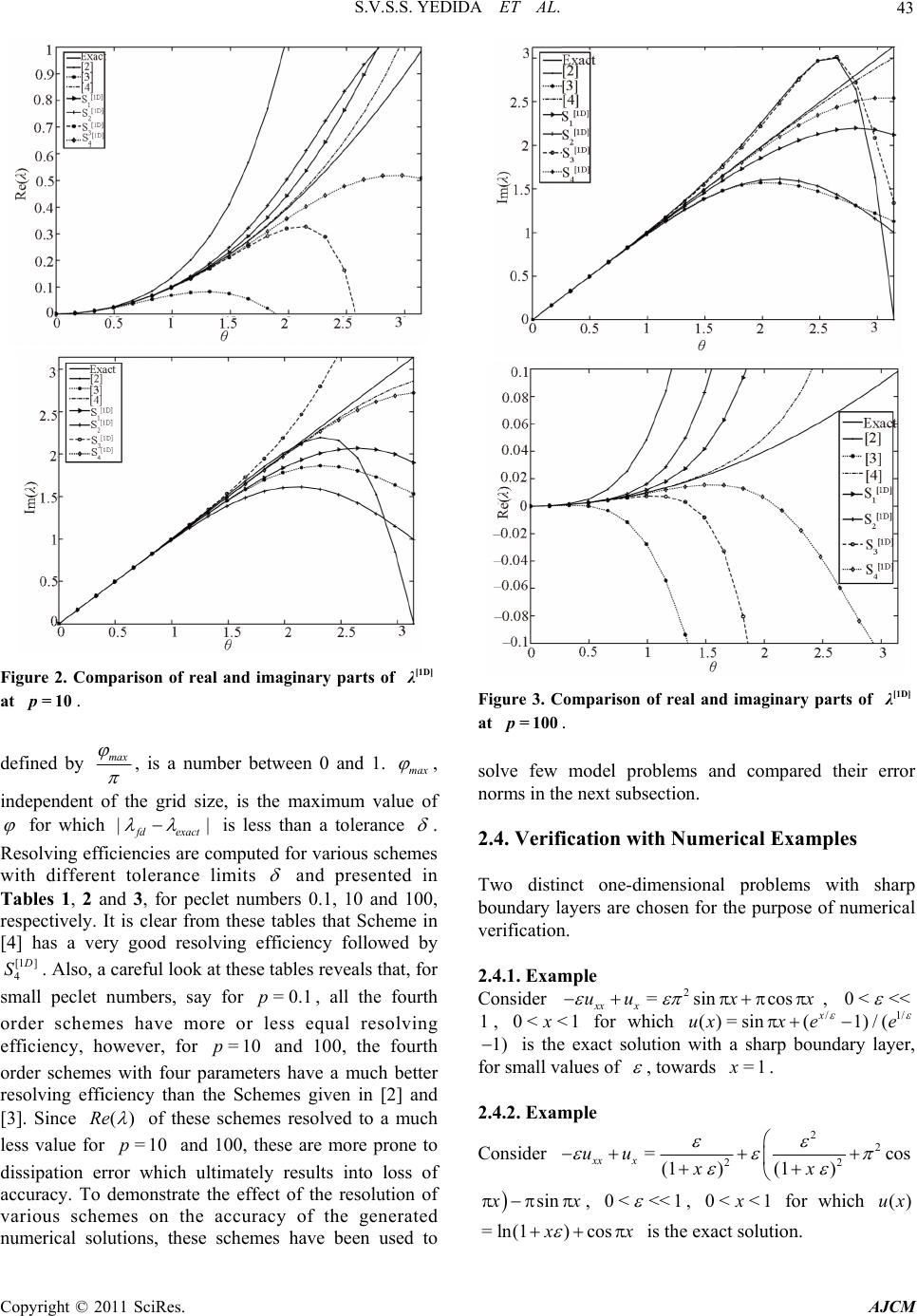 S.V.S.S. YEDIDA ET AL. 43 Figure 2. Comparison of real and imaginary parts of defined by [1D] λ at =10p. max , is a number between 0 and 1. max , e ofindependent of the grid size, is the maximum valu fohicr wh || f d exact Figure 3. Comparison of real and imaginary parts of at solve few model problems and compared their error norms in the next subsection. Two distinct one-dimensional problems with sharp Consider x [1D] λ = 100p. 2.4. Verification with Numerical Examples is less than a tolerance . hemesResolving efficiencies aremputed for various sc co olerance limwith different tits and presented Tables 1, 2 and3, for peclet numbers 0.1, 10 and, respectively. It is clear from these tables that Scheme in [] has a veryving efficiency followed by [1 ] 4 in 100 good resol4 D S. Also, a careful look at these tables reveals that, for small peclet numbers, say for 0.1p, all the fourth order schemes have more or less equal resolving efficiency, however, for =10p and 100, the fourth order schemes with four parameters have a much better ving efficiency than the Schemes given in [2] and [3]. Since ()Re = resol of these schemlved to a much less value for =10p and 100, these are more prone to dissipation error which ulty results into loss of accuracy. To demonstrate the effect of the resolution of various schemes on the accuracy of the generated numerical sns, these schemes have been used to es reso boundary layers are chosen for the purpose of numerical verification. 2.4.1. Example 2 =sin cos xx x uu x 0< <<, 1, 0< <1x for which /1/ ()=sin (1)/( x uxx ee 1) is the exact solution with a sharp boundary layer, for small values of , towards =1x. 2.4.2. Example imatel olutio Csider on22 22 = (1 )(1 ) xx x uu xx sin cos x x , 0< <<1 , 0< fo<1xr which ()ux =ln(1) cos x x is the exn. act solutio Copyright © 2011 SciRes. AJCM 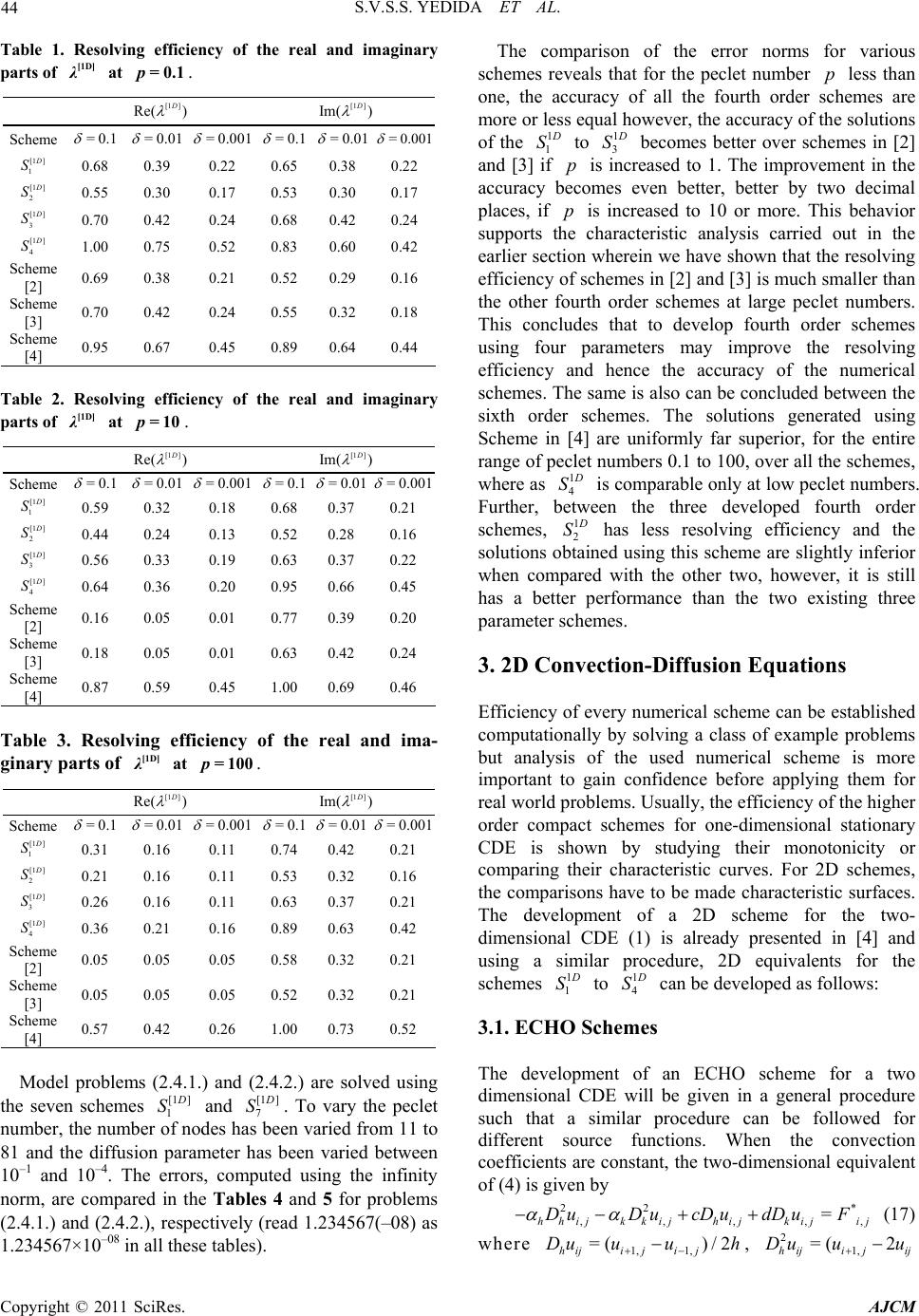 S.V.S.S. YEDIDA ET AL. 44 Table 1. Resolving efficiency of the real and imaginary [1D] at =0.1p. parts of λ [1 ] Im( ) D [1 ] Re( ) D Scheme =0.1 =0 .01 = 0.001 =0.1 =0 .01 = 0.001 [1 ] 1 D S 0.68 0.39 0.22 0.65 0.38 0.22 [1 ] 2 D S 0.55 0.30 0.17 0.53 0.30 0.17 [1 ] 3 D S 70 0.0.0.42 24 0.68 0.42 0.24 [1 ] 4 D S 1.00 0.75 0.52 0.83 0.60 0.42 Scheme 0.69 0.38 0.21 0.52 0.29 0.16 Schem [3] Schem [4] [2] e0.70 0.42 0.24 0.55 0.32 0.18 e0.95 0.67 0.45 0.89 0.64 0.44 Table . Ringcien thl ma pλt p. 2esolv efficy ofe reaand iginary arts of [1D] a=10 [1 ] e( D R) [1 ] (D Im) Scheme =0.1 =0.01 = 0.001 =0.1 =0.01 =0.001 [1 ] 1 D S 0.59 0.32 0.18 0.68 0.37 0.21 [1 ] 2 D S 0.44 0.24 0.13 0.52 0.28 0.16 [1 ] 3 D S 56 [1 ] 0.0.33 0.19 0.63 0.37 0.22 4 D S Sch 0.64 0.36 0.20 0.95 0.66 0.45 e 0.16 0.05 0.01 0.77 0.39 0.20 Schem [3] Schem [4] em [2] e 0.18 0.05 0.01 0.63 0.42 0.24 e 0.87 0.59 0.45 1.00 0.69 0.46 Table3. lviffic of r ga λt 0p. Resong eiency theeal and ima- inary prts of[1D] a=10 [1 ] e( D R) [1 ] (D Im) Scheme =0.1 =0.01 =0.001 =0.1 =0.01 =0.001 [1 ] 1 D S 0.31 0.16 0.11 0.74 0.42 0.21 [1 ] 2 D S 0.21 0.16 0.11 0.53 0.32 0.16 [1 ] 3 D S 0.26 0.63 0.37 0.21 [1 ] 0.16 0.11 4 D S Sch e 0.36 0.21 0.16 0.89 0.63 0.42 0.05 0.05 0.05 0.58 0.32 0.21 Schem [3] Schem [4] em [2] e0.05 0.05 0.05 0.52 0.32 0.21 e0.57 0.42 0.26 1.00 0.73 0.52 Mol .1.) (2.edg tn es deproblems (2.4 and4.2.) are solv usin he seveschem [1 1] D S and [1 7] D S. To heet nthmber desriomto 81 theusiramhasn v bn 1 Thorsputy or pared in the Tables 4 and 5 for problems 1.2 of the error vary t pecl umber, ande nu diffof on pa no has bee eter n va beeed fr aried 11 etwee 0–1 and m, are com 10–4. e err, comted using the infini n (2.4.1.) and (2.4.2.), respectively (read 1.234567(–08) as 34567×10 –08 in all these tables). The comparison norms for various schemes reveals that for the peclet number p less than one, the accuracy of all the fourth order schemes are more or less equal however, the accuracy of the solutions of the 1 1 D S to 1 3 D S becomes better over schemes in [2] and [3] if p is increased to 1. The improvement in the accuracy becomes even better, better bydecimal pl two o aces, if p is increased to 10 or more. This behavior supports the characteristic analysis carriedut in the earlier section wherein we have shown that the resolving efficiency of schemes in [2] and [3] is much smaller than the othurther schemes at large peclet numbers. This concles that to develop fourth order schemes using four parameters may improve the resolving efficiency nd hence the accuracy of the numerical schemes. The same is also can be concluded between the sixth order schemes. The solutions generated using Scheme in [4] are uniformly far superior, for the entire range of peclet numbers 0.1 to 100, over all the schemes, wher e as 1 4 er fo u a ord d D S is comparable only at low peclet numbers. Further, between the three developed fourth order schemes, 1 2 D S has less resolving efficiency and the solutions obtained using this scheme are slightly inferior when compared with the other two, however, it is still has a better performance than the two existing three parameter schemes. 3. 2D Convection-Diffusion Equations Efficiency of every numerical scheme can be established computationally by solving a class of example problems but analysis of the used numerical scheme is more important to gain confidence before applying them for real world problems. Usually, the efficiency of the higher ionary city or order compact schemes for one-dimensional stat CDE is shown by studying their monotoni comparing their characteristic curves. For 2D schemes, the comparisons have to be made characteristic surfaces. The development of a 2D scheme for the two- dimensional CDE (1) is already presented in [4] and using a similar procedure, 2D equivalents for the schemes 1 1 D S to 1 4 D S can be developed as follows: 3.1. ECHO Schemes The development of an ECHO scheme for a two dimensional CDE will be given in a general procedure such that a similar procedure can be followed for different urce nctions. When the convection coefficients ae constant, the two-dimensional equivalent so fu r * (17) of (4) is given by 22 ,,,,, where 1, 1, =( )/2 hiji ji j Du uuh = hhijkkijh ijkijij DuDucDu dDuF , 21, =( 2 hijijij Du uu Copyright © 2011 SciRes. AJCM 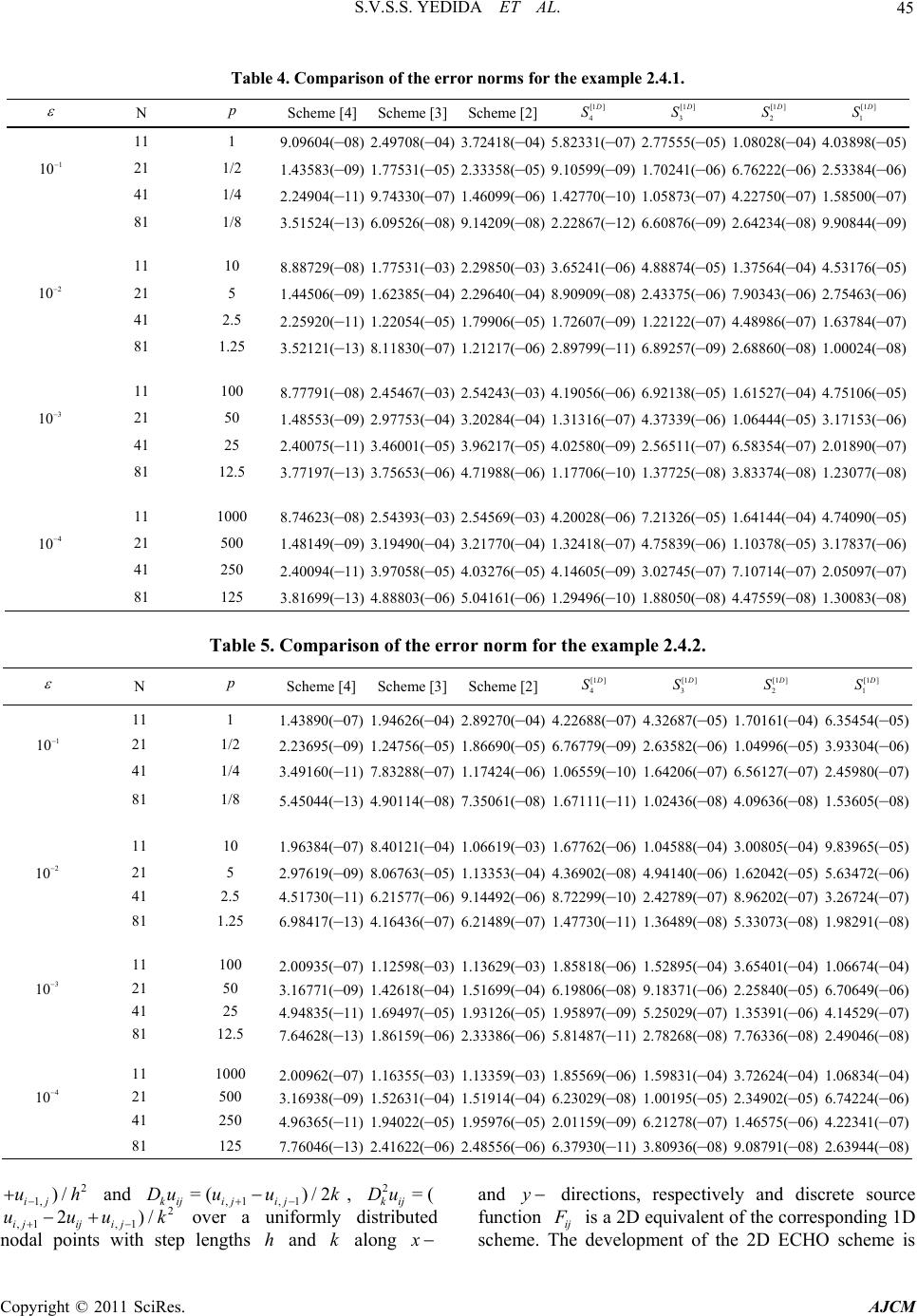 S.V.S.S. YEDIDA ET AL. Copyright © 2011 SciRes. AJCM 45 orr the example 2.4.1. Table 4. Comparison of the err norms fo N p Scheme [4] S cheme [3][1 ] 4 D S [1 ] 3 D S [1 ] 2 D S [1] 1 D S Scheme [2] 11 1 9.09604(–08)2.49708(–04) 3.72418(–04)5.82331(–07)2.77555(–05) 1.08028(–04) 4.03898(–05) 1 10 21 1/2 06) 6.76222(–06) 2.53384(–06) 41 107) 4.22750(–07) 1.58500(–07) 81 1/86 9 2.22867(2)6.60876(9) 2.64234(8) 9.90844() 8 1 3.5212 (–13)8.1183(–07)1.2121(–06)2.8979(–11) 6.8925(–09) 2.6886(–08) 1.0002(–08) 1 8 1 3.7719 (–13)3.7565(–06)4.7198(–06)1.1770(–10) 1.3772(–08) 3.8337(–08) 1.2307(–08) 1 8 1 3.8169 (–13)4.8880(–06)5.0416(–06)1.2949(–10) 1.8805(–08) 4.4755(–08) 1.3008(–08) 1.43583(–09)1.77531(–05)2.33358(–05)9.10599(–09) 1.70241(– /4 2.24904(–11)9.74330(–07)1.46099(–06) 1.42770(–10)1.05873(– 3.51524(–13) .09526(–08) .14209(–08) –1–0–0–09 11 10 8.88729(–08)1.77531(–03)2.29850(–03) 3.65241(–06)4.88874(–05) 1.37564(–04) 4.53176(–05) 2 10 21 5 1.44506(–09)1.62385(–04)2.29640(–04) 8.90909(–08) 2.43375(–06) 7.90343(–06) 2.75463(–06) 41 2.5 2.25920(–11)1.22054(–05)1.79906(–05) 1.72607(–09)1.22122(–07) 4.48986(–07) 1.63784(–07) 1.25107970 4 11 008.77791(–08) 2.45467(–03) 2.54243(–03) 4.19056(–06) 6.92138(–05) 1.61527(–04) 4.75106(–05) 3 10 21 50 1.48553(–09)2.97753(–04)3.20284(–04) 1.31316(–07) 4.37339(–06) 1.06444(–05) 3.17153(–06) 41 25 2.40075(–11)3.46001(–05)3.96217(–05) 4.02580(–09)2.56511(–07) 6.58354(–07) 2.01890(–07) 12.5738654 7 11 0008.74623(–08) 2.54393(–03)2.54569(–03) 4.20028(–06) 7.21326(–05) 1.64144(–04) 4.74090(–05) 4 10 21 500 1.48149(–09)3.19490(–04)3.21770(–04) 1.32418(–07)4.75839(–06) 1.10378(–05) 3.17837(–06) 41 250 2.40094(–11)3.97058(–05)4.03276(–05) 4.14605(–09)3.02745(–07) 7.10714(–07) 2.05097(–07) 1 25 931609 3 T 5.able Comparison of the error norm for the example 2.4.2. N p Scheme [4] Scheme [3]Scheme [2][1 ] 4 D S [1 ] 3 D S [1 ] 2 D S [1 ] 1 D S 11 1 1.43890(07)1.94626(04)2.89270(04)4.22688(07)4.32687( 05) 1.70161(04) 6.35454(05) – – – – – – – 1 10 21 ) 1.04996(–05) 3.93304(–06) 41 1/4 3.49160(–11) 7.83288(–07) 1.17424(–06) 1.06559(–10) 1.64206(–07) 6.56127(–07) 2.45980(–07) 81 1/8547) 1.67111(11) 1.02436(8) 4.09636(8) 1.53605() 8 1 6.9841 (13)4.1643 (07)6.2148 (07)1.4773 (11)1.3648 (08) 5.3307(08) 1.9829(08 ) 100 1/2 2.23695(–09) 1.24756(–05) 1.86690(–05) 6.76779(–09) 2.63582(–06 .45044(–13).90114(–08).35061(–08 – –0–0–08 11 10 1.96384(–07)8.40121(–04) 1.06619(–03) 1.67762(–06) 1.04588(–04) 3.00805(–04) 9.83965(–05) 2 10 21 5 2.97619(–09)8.06763(–05) 1.13353(–04) 4.36902(–08) 4.94140(–06) 1.62042(–05) 5.63472(–06) 41 2.5 4.51730(–11) – 6.21577(–06) – 9.14492(–06) – 8.72299(–10) – 2.42789(–07) – 8.96202(–07) – 3.26724(–07) – 1.25 7690931 11 2.00935(–07)1.12598(–03) 1.13629(–03) 1.85818(–06) 1.52895(–04) 3.65401(–04) 1.06674(–04) 3 10 21 50 3.16771(–09) 4.94835(–11) 1.42618(–04) 1.69497(–05) 1.51699(–04) 1.93126(–05) 6.19806(–08) 1.95897(–09) 9.18371(–06) 2.2584 5.25029(–07) 0(–05) 6.7064 1.35391(–06) 9(–06) 4.14529(–07) 41 25 81 12.5 7.64628(–13)1.86159(–06) 2.33386(–06) 5.81487(–11) 2.78268(–08) 7.76336(–08) 2.49046(–08) 11 1000 2.00962(–07)1.16355(–03) 1.13359(–03) 1.85569(–06) 1.59831(–04) 3.72624(–04) 1.06834(–04) 4 10 21 500 3.16938(–09)1.52631(–04) 1.51914(–04) 6.23029(–08) 1.00195(–05) 2.34902(–05) 6.74224(–06) 41 250 4.96365(–11)1.94022(–05) 1.95976(–05) 2.01159(–09) 6.21278(–07) 1.46575(–06) 4.22341(–07) 81 125 7.76046(–13)2.41622(–06) 2.48556(–06) 6.37930(–11) 3.80936(–08) 9.08791(–08) 2.63944(–08) and 2 1, ) ij uh ,1 ij ij uu nodal poin 2=( kij Du / D,1ij,1 )/2 ijk , =( kij u uu 2 k ove uniforml step lengths h and k , 2) ij u ts with 1/ r ay di alstributed ong x and y directions, respectively and discrete source function ij F is a 2D developm e e quivalent of ent of th the corresp 2D ECHOonding 1D scheme isscheme. The  46 given ellow for erent seon 3.1.1. Schem S.V.S.S. YEDIDA ET AL. bdifflectiof source functions. e [1 1D] S urce Consider the sofu (18)puted using Taylor series , nction, which is an extension of the scheme 2.1.1., given by *11,2 31,4 1,1 23,1 4 =() () ijijijx i ijijijy ij Fcf cfcfcf dfdfdfdf (18) The truncation error of the scheme (17) with the ij source function com expansion, is g iy, ven b , =, 4 ,, () x yij TE EuGuHu xyyij xxyij xxyyi ji j Ku fOh (19) where , 11 =EdKcL, 12 =GbKcL 21 = H dK aL , 22 = K bK aL 2 13142 31 131 =(), =()/2, =( ) Khcc cK hcc Lkdd (20) 2 42 31 , =()/2dL kdd Expanding the terms in (19) and (20) sh scheme (17) is of second order accurate. fourth order, the scheme and the source function is as e coefficients and , are given by ows that the To make it written 2 2 2222 = hh kkhkhk khh kh kijij DDcDdDEDD GD DHD DKD DuF (21) ,11,2,31,4, 1,12,3,1 4, = ijijiji jxij ijijijyij Fcf cfcf cf dfdf dfdf where th i ci d=1, 2, 3&4i 32 2 11 = 30.530.25 6 x xxxxxx cx , 2 22 =2 2 3 x xx c , 32 2 3=30.5 3 6 10.25 x xxx cxxxx , 32 2 11 = 30.530.25 6 y yyyyyyy d , 2 22 =2 2 3 y yy d , 32 2 31 = 30.530.25 6 y yyyyyy dy , 32 4=(60.5 6) y yyy dh , = x a ch , = y a dk , =h xch , and =k ydk for and not equal to zero cd and 11, =c12 25, =c631 =c12, =0c4, 11 =d12 , 25 =6 d, 31 =12 d, 4=0d when. Similarly, for the other selection of source functions remainder terms are utilized to get fourth order accuracy. For every sche 0==cd me , E, G H K aras i and e same n (20) but 1 K , 2 K , 1 2 L and L vawith the scheme. 3.1.2. Scheme ries [1D] 2 S Let 1,j 2 1 ) (() yij j d f 11,2 3 1,1 3, 11232 31 =()(() )() =, =(), ii xijxijxi yij yi Ffcfcf cf df df KcccK hcc 11 232 31 =, =() LdddL kdd The coefficients t dcrete sorce function are given by (22) in heisu 32 12 11 0.5 61 =10.5 12 2 x xx x xx xx ch , 3 225 =2 2 36 2 x xxx ch x , 32 0.5 61 2 xx x 32 11 =10.5 12 x xx xx ch , 32 12 11 0.5 61 =10.5 12 yyy 2 y yy yy dk , 32 225 =2 2 36 y yyy dk y , 32 32 11 0.5 61 =10.5 12 yyy 2 y yy yy dk 1=24 h c , 2=0c, 3=24 h for =0cd c, and 1=24 k d , 2=0d, 3=24 k d when ==0cd . 3.1.3. Scheme [1D] 3 S =( Let ) 12 3 12 3 112 21 122 )()( ()()() =, =, =, =, ij ijxijxxijxxxij y ijyy ijyyy ij Fff cfcf dfd fdf c K cKc LdLd (23) Copyright © 2011 SciRes. AJCM  S.V.S.S. YEDIDA ET AL. 47 coefficienhe discrete source funre n by Thets in tction a give 1=( ) x x ch , 22 1 =6 2 x x cx h , 33 3=2 11 612 x xxx x ch , 1=( ) y y dk , 22 21 =6 y yy dk , 33 2 11 = 361 2 y yyy y dk d not equal to zero and , for cand 1=0c 2 2=12 h c, 3 c=0, , 1=0d 2 2=12 k d, . 3.1.4. Scheme 3=0d when ==0 cd [1D] 4 S Let 11, 231, 45 11,2 31, 45 2 143125 142 3 =(), = ( ( 2 31 2 31 51 = ()() ()() (), 2 =), =), iijijij xixxii ji ijyiyyi ij Fccf cf cf cfdfdf dfd fdff h j f K c c dd dd (24) The coefficients in the discrete source function are hccK cc k Ldk Ld given by 43 2 1=123(14)(2 3) (0.5)(0.10.25) x xxx xx x cx , 432 2=24 244 20. xxxxxx c 43 2 3=123(1 4)(2 3) (0.5)(0.10.25) 8 , x xxx xx x cx , 32 4=(660.5) x xx x ch , 24 3 2 51 =1212 15 xxxx ch , 43 2 1=123(14)(23) (0.5)(0.10.25) y yyyy yy y d 432 2=24 244 20.8 yyyyyy d , , 43 2 3=123(1 4)(2 3) y yyy dy (0.5)(0.1 0.25) y yy , 32 4=(6 60.5) y yy y dk , 24 3 2 51 =1212 15 yyyy dk for c and d not equal to zero and 11 =30 c, 214 =15 c, 3 c1 =30 , c4=0, 2 5=20 h c, 11 =30 d, 214 =15 d, 31 30 , =d4=0d, 2 5=20 k d when. These four different schemes 3.1.3.1.4. are compared with the existing ECHO schemes given in [2] and [3]. 2D Scheme in [2] : Let ==0cd 1.- 11, 231, 11, 231, 2 1312 31 2 131231 =(), =(), 2 = 2 Fcfcf cf f =(), =(), iijijij i jiji jij df d fd f h hccK cc k K Lk ddLdd (25) The coefficients in the discrete source function are given by 11 = ()( xx c 22 =2( 3 0.5) 6x , ) x xx c , 31 = ()(0.5) 6xxx c , 11 = (d22 =2)( 0.5) 6yyy , () y 3yy d , 31 = ()(0.5) 6xxx d d not equal to zero and for c and 11 =12 c, 25 =6 c, 31 12 , =c11 =12 d, 25 =31 =12 d 6 d, when 2D Scheme in [3] : Let ==0cd . ,12, 12 112 21 122 =()() ()() =, =, =, =, iij xijxxij yijyy ij Ff cfcf dfdf f K cKc LdLd (26) eurce fution a given by Th coefficients in the discrete soncre 1=( ) x x ch , 2 2=(0. ( xx x ch5 )) , 1=( ) x x dh , 2 2=(0 () xx x dh.5 ) o zero and for c and d not equal t1=0c, 2 2=12 h c, Copyright © 2011 SciRes. AJCM  48 S.V.S.S. YEDIDA ET AL. 1=0d, 2 2=12 h d 3.2. Comparison of the Characteristic when ==0 cd . Surfaces istic surface of tial equation is obtaineds et nu The character in term a differen mbers of pecl= x pc a and h = y dk pa, in x and dipectively. Equation (1), obtained by yrections, res g () The characteristic of the governin substituting I wx wy x y e gi in the place of the depend isent va riable u, ven by : 2 [2 ]2 1 =yyy D xxx p cd rIpr apprr xy (27) where = x x wh , = x y wk are phase angles and x w, y w are the wave numbers, h and k arengths step le and =1I diffe . Sime charatic surfa c ) ilarly, th he alscterisce of any rence sme is obtained by substituting o (Ii j x y e for in the difference scheme. Following ij this procedure, the characteristic surfaces of the 2D schemes [2 ] 1 u D S to [2 ] 4 D S ted and the same are given by Characteristic Surface for [1 D] are compu 1 S : 212 134 1 = D xy zIz cd appzIz (28) 1 22 11 11 (2cos 2)(2cos2) k xy xy r rp 2 =2(1cos)(1cos) (1)(1) sinsin k hxy yx rr ppr 66 x h z pr r rr p hh xy y p ; 2 2 =sin sin 1 (1)sin (2cos2) 6 (1)(1) (2cos2)sin 6 y xxy xh kxy yx yy hkx y x p zpr r pr r ppr pp r rp rp y 322 3131 = (1)()cos()cos ; x y z , 4313144 =()sin()sin x yx zy where =coth 22 x x h pp , =coth 22 y y k pp , 132 3(1)12 1 =64 hhh x xx p pp , 22 2(1 ) 2 =3 h x p , 332 3(1) 12 1 =64 hhh x xx p pp , 43 6(1 ) =2 hh x xp p . ilarly, Sim 13(1 1 =32 ) 12 64 kkk y yy p pp , 22 2(1 ) 2 =3 k y p , 332 3(1) 12 1 =64 kkk y yy p pp , 43 6(1 ) =2 kk y yp p . The terms and in the denominator of (28) are the contribudue to the source function of the scheme andhence from scheme to scheme. However, all the exponential schemes are same as in (28). Tjustify this, one can expand 3 z tions the num 4 z vary erator of o 1 K , 2 K , 1 L and 2 L each case with their parameters for every and i they appear like schemen 1=h a Kc , 2 22 () =6 h aa h Kc , 1=k b Ld , 2 22 () =6 k bb k Ld . Therefore, the characteristics of the schemes are differ byih their denomnator wich contains the contribution of the source function of the scheme. The characteristic surfaces of the remaining three schemes are Characteristic Surface for [1D] 2 S : [2 ]12 234 1 = D xy zIz cd appzIz (29) 331 31 =1 ()sin()cos x xy zy , 42 23131 =()cos()cos x yxxy z y , 132 112 1 =12 12 2 hh h x xx p pp , 23 52(1) 2 =36 hh xx x pp p , 332 112 1 =12 12 2 hh h x xx p pp , 132 11 =kk k 21 12 12 2y yy p pp , 23 52(1) 2 =36 kk yy y pp p , Copyright © 2011 SciRes. AJCM  S.V.S.S. YEDIDA ET AL. 49 332 112 1 =12 12 2 kkk y yy p pp teristic Surface for [1D] 3 ; Charac S : 212 334 1 = D xy zIz cd appzIz 22 322 (30) =1 x y z , 33 41 133 = x yx zy , 11 =h x p , 21 =62 1h x p , 33 12 =12 hh x xp p , 11 =k y p , 22 1 1 =6 k y p , 33 12 =12 kk y yp p , Characteristic Surface for [1 D] 4 S : 21 41 = DzI cd 2 34 xy z appzIz (31) 322 31 22 3155 =(1) ()cos ()cos x y xy z , 43131 4 )sin ()sin4 =( x yxy z , 1432 12(1)3(1) 221 =410 hhhh x xxx p ppp , 232 24(1)2(2) 4 =5 hh xx pp , 3432 12(1) 3(1) =hhh 2 21 410 h x xxx p ppp , 43 6(1) =2 hh x xp p , 542 12(1) 11 ; =15 h xx pp 1432 12(1 )3(1 )221 =41 kkk 0 y yy y p ppp , k 232 24(1) 2(2) 4 =5 kk yy pp , 3432 12(1 )3(1)221 =41 kkkk 0 yy y pp p , y p 45 34 6(1)12(1)11 =,= 2 2 1 kk k y yyy p ppp ; Similarly, the characteristics of the schemes in [2] and [3] are derived and giveny Characteristic Surface for Scheme [2]: 5 b [2] 12 34 1 = xy ziz cd appziz ( 2) 3 322 3131 = (1)()cos()cos x y z , 431 31 =()sin()sin 11 =h x p , 22 1 1 =6 h x p , 11 =k y p , 22 1 1 =6 k y p . Characteristic Surface for Scheme [3]: [3] 12 1 =ziz cd 34 xy ap p z iz (33) 1 22 32241 =1, = x yx zz y , x y z , 11 =h x p , 22 1 1 =6 h x p , 11 =k y p , 22 1 1 =6 k y p . The characteristic surfaces defined in (28-31) are symmetric or antisymmetric in the region [0, ] [0, ] depending on whether [2 ] D i is an even or odd function of x p and y p. Further they are al 2so periodic with period . These surfaces [2 ] D i , with respect to 0x p and 0y p , arison, r can t ho nsional case, it is difficult to visualize the closeness arisons are m ns f o be pl wever, y, comp rom the o ted together for unlike in one the shak dime of these surfac different a if = e n of com r c p es. Alternativel oss sectio ade at Further, gularigin. x y r pp curve, the, they are also sym efore, in thepresm h e characteristics are comped at 15˚, 30˚ 45˚ cross sections. etric w ent case, tit h respect to 45˚ values of the ar and The characteristics at the three chosen cross sections are plotted against the exact one in Figures 4 and 5 for ==10pp and = =100 xy pp , respectively. The comparisons of the real parts of the characteristics are included in the first column of these figures, while the comparisons of the imaginary parts are shown in the second column. The three rows in these figures stand for the comparisons at 15˚, 30˚ and 45˚ cross sections, respectively. It can be seen clearly in each of these figures that the characteristics of the existing three parameter 2D schemes are far away from the exact curve compared to the four parameter schemes which have been developed in this work. Interestingly, the deviation is increased with angle and also wi xy th peclet number giving a very substantial deviation at ==100 xy pp . Particularly, Scheme in [2] is deviated more at the center and also produced a significant overshoot for all most all the cross sections. Among the present four parameter based fourth order 2D schemes, [2 ] 2 D S produced minimum and [2 ] 3 D S produced maximum dissipation errors. However, when Copyright © 2011 SciRes. AJCM  S.V.S.S. YEDIDA ET AL. Copyright © 2011 SciRes. AJCM 50 (a) (b) Figure 4. Comparison of the (a) real and (b) imaginary parts of the characteristic at the peclet number is increased to 100, 10 xy p=p= . [2 ] 2 D S here is overshot the exact characteristic in its real part but tno such abnormality with respect to [2 ] 3 D S. A similarovershoot in its real part is also been observed in [2 ] 1 D Sparts, at least along 15˚ cross section. For the imaginary [2 ] 3 D S has the minimum and [2 ] 2 D S has the high deviation 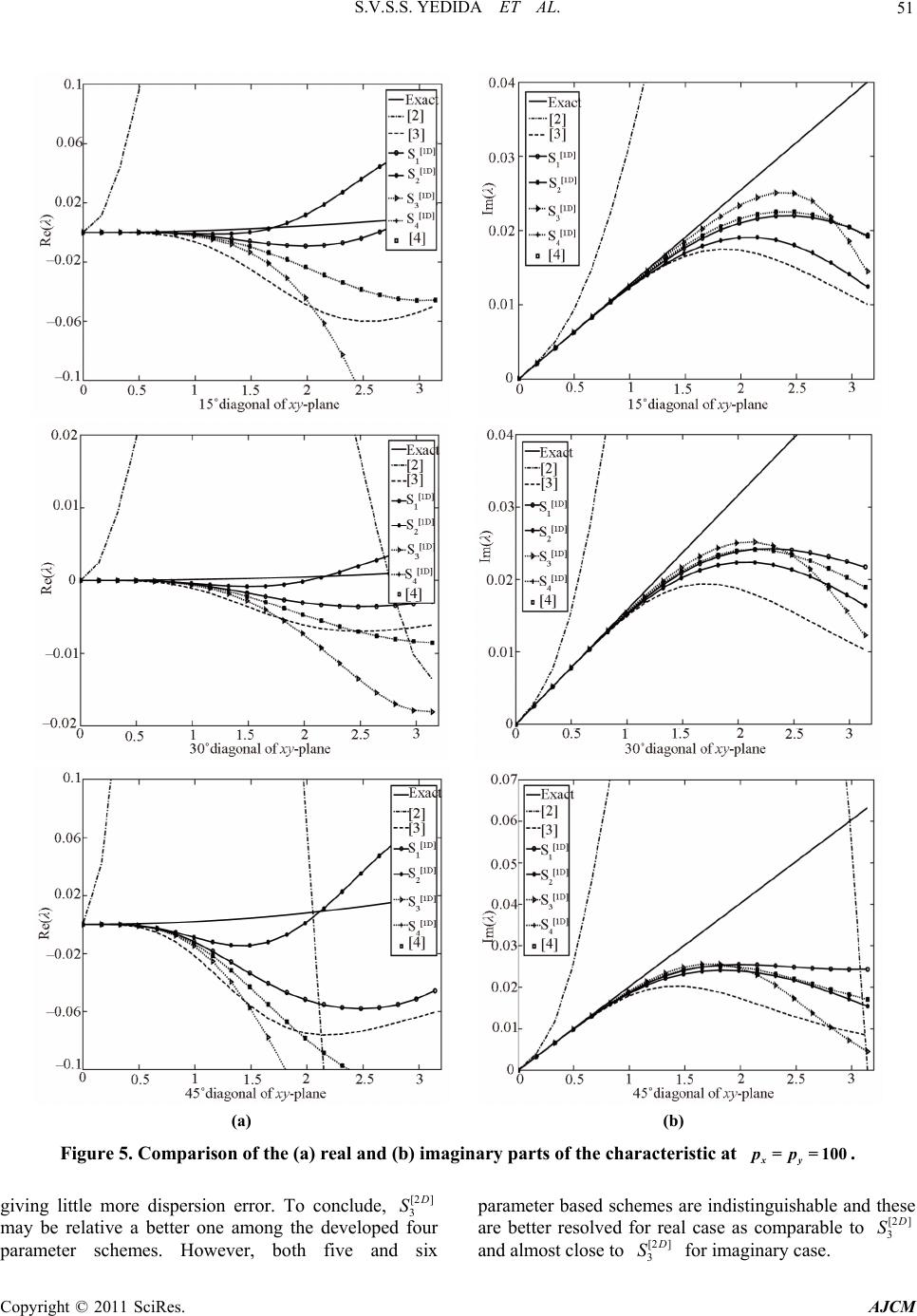 S.V.S.S. YEDIDA ET AL. 51 (a) (b) Figure 5. Comparison of the (a) real and (b) imaginary parts of the characteristic at giving little more dispersion error. To conclude, 100 xy p=p= . [2 ] 3 D S four d six may be relative a better one among the developed parameter schemes. However, both five an parameter based schemes are indistinguishable and these are better resolved for real case as comparable to [2 ] 3 D S for imaginary case. and almost close to [2 ] 3 D S Copyright © 2011 SciRes. AJCM 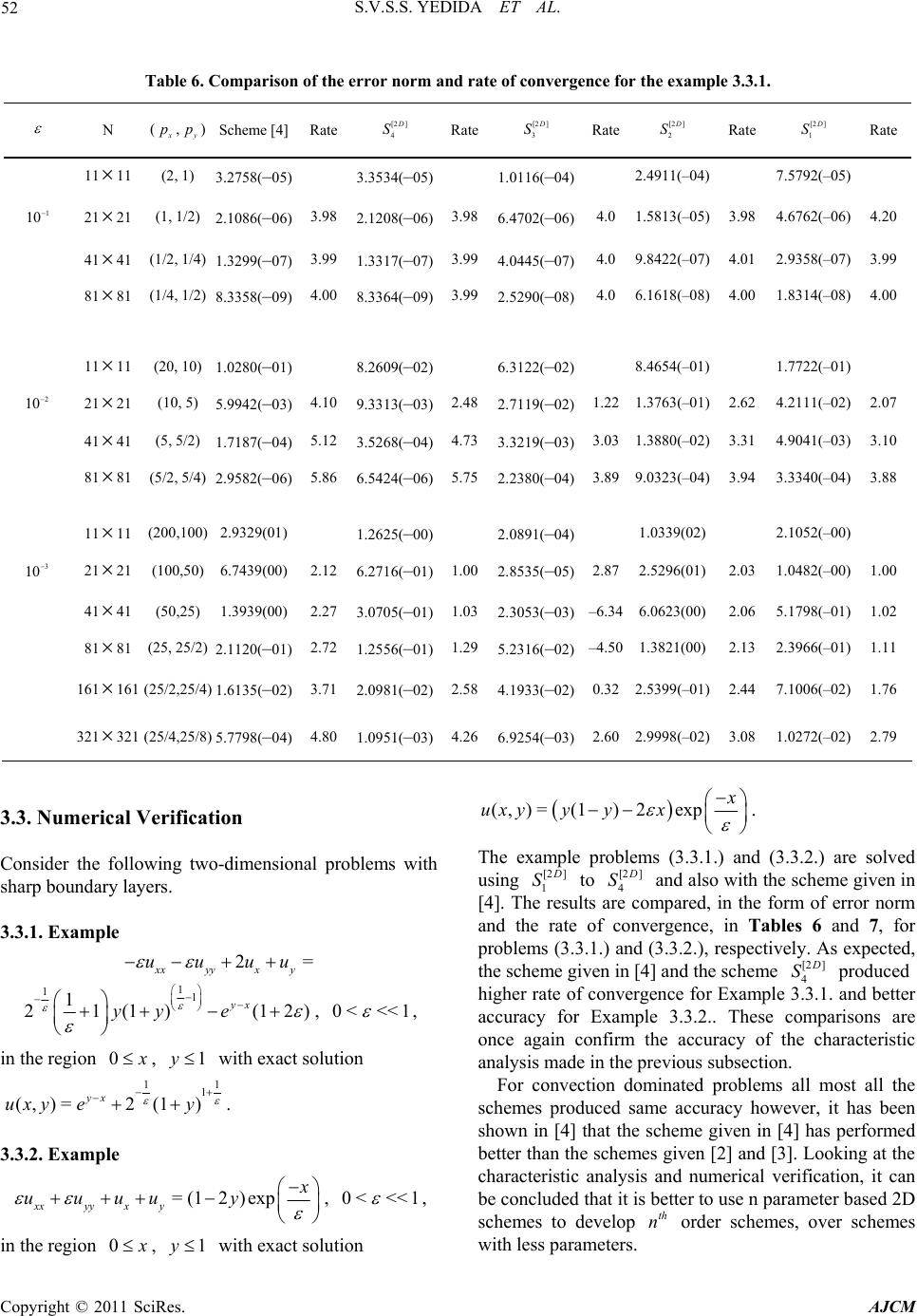 S.V.S.S. YEDIDA ET AL. 52 Table 6. Comparison of the error norm and rate of convergence for the example 3.3.1. N ( x p ,y p ) Scheme [4] Rate [2] 4 D S Rate [2] 3 D S Rate [2] 2 D S Rate [2] 1 D S Rate 1111 (2, 1) 3.2758(–05) 3.3534(–05) 1.0116(–04) 2.4911(–04) 7.5792(–05) 1 10 2121 (1, 1/2) 2.1086(–06) 3.98 2.1208(–06) 3.986.4702(–06) 4.0 1.5813(–05) 3.98 4.6762(–06)4.20 4141 (1/2, 1/4) 1.3299(–07) 3.99 1.3317(–07)3.99 4.0445(–07)4.0 9.8422(–07) 4.01 2.9358(–07)3.99 8181 (1/4, 1/2) 8.3358(–09) 4.00 8.3364(–09)3.99 2.5290(–08)4.0 6.1618(–08) 4.00 1.8314(–08)4.00 1111 (20, 10) 1.0280(–01) 8.2609(–02) 6.3122(–02) 8.4654(–01) 1.7722(–01) 2121 (10, 5) 5.9942(–03) 4.10 9.3313(–03) 2.482.7119(–02)1.22 1.3763(–01) 2.62 4.2111(–02)2.07 4141 (5, 5/2) 1.7187(–04) 5.12 3.5268(–04)4.73 3.3219(–03)3.031.3880(–02) 3.31 4.9041(–03)3.10 8181 (5/2, 5/4) 2.9582(–06) 5.86 6.5424(–06)5.75 2.2380(–04)3.899.0323(–04) 3.94 3.3340(–04)3.88 1111 (200,100) 2.9329(01) 1.2625(–00) 2.0891(–04) 1.0339(02) 2.1052(–00) 2121 (100,50) 6.7439(00) 2.12 6.2716(–01)1.00 2.8535(–05)2.872.5296(01) 2.03 1.0482(–00)1.00 4141 (50,25) 1.3939(00) 2.27 3.0705(–01)1.03 2.3053(–03)–6.346.0623(00) 2.06 5.1798(–01)1.02 8181 (25, 25/2) 2.1120(–01) 2.72 1.2556(–01)1.29 5.2316(–02)–4.501.3821(00) 2.13 2.3966(–01)1.11 161161 (25/2,25/4) 1.6135(–02) 3.71 2.0981(–02) 2.584.1933(–02)0.32 2.5399(–01) 2.44 7.1006(–02)1.76 321321 (25/4,25/8) 5. 2) 3.08 1.0272(–02)2.79 2 10 3 10 7798(–04) 4.80 1.0951(–03) 4.266.9254(–03)2.60 2.9998(–0 3.3.1. Example 3.3. Numerical Verification Consider the following two-dimensional problems with sharp boundary layers. 2= xxyyx y uuuu 1 11 1 21(1) (12) yx yye , 0< << 1 , in the gireon 0 x , 1y with exact solution 11 1 (,)=uxe 2 yx (1 )yy . 3.3.2. Example =(12)exp xxyyx y x uuuu y , 0< <<1 , in the region 0 x , 1y (, )=(1)2exp x uxyy yx ms (re solved using . he example proble3.3.1.) and (3.3.2.) aT[2] 1 D S to [2 ] 4 D S s are com [4 and also with the scheme given in [4]. Thepared, in the form of error norm s 6 and 7, for As expected, given in] and the scheme result hem and the rate of convergence, in Tabl e problems (3.3 .1.) and (3.3.2.), respectively. the sce[2 ] 4 D S ple 3.3.1. a pro higher nce for End accuracy for Exam Teseonsare once aconfirmacy of the r n eio For convection dominated problems all most all the cuswan shown in4] that the scheme given in [4] has performed ee m2 ge charactistic analysis an numerical verifiation, ian be concluded that it is better to use n parameter based 2D scevelop schemches with less parameters. duced betterrate of convergexam ple 3.3.2.. the accurh comparis characte istic gain aalysis madein th previous subsectn. shemes prodced ame accuracy hoever, it hs bee [ tter than thbschees given [] and[3 ]. Lookin at th erdct c hemes to d th n orderes, over sem with exact solution Copyright © 2011 SciRes. AJCM 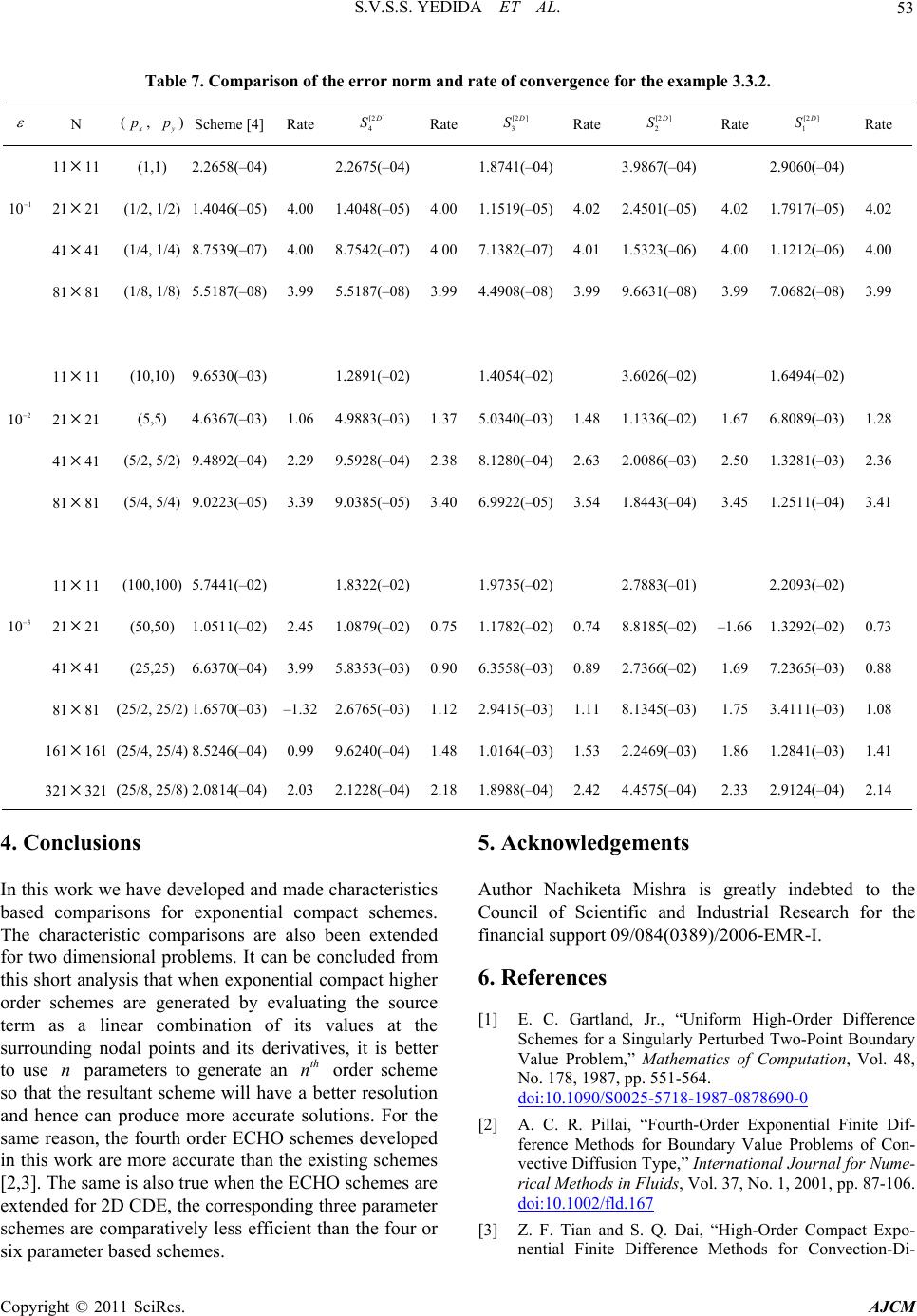 S.V.S.S. YEDIDA ET AL. 53 Table 7. Comparison of the error nd rate of conergence for the example 3.3.2. orm anv ( x p , y p ) Scheme [4] Ra[2 ] N te 4 D S R[2] ate 3 D S R[2] ate 2 D S Rate [2 ] 1 D S Rate 1111 (1,1) 2.2658(–04) 2.2675(–04) 1.8741(–04) 3.9867(–04) 2.9060(–04) 1 10 2121 (1/2, 1/ 2) 1.4046(–05) 4.00 1.4048(–05)4.00 1.1519(–05)4.02 2.4501(–05) 4.02 1.7917(–05)4.02 4141 (1/4, 1/4) 8.7539(–07) 4.00 8.7542(–07)4.00 7.1382(–07)4.01 1.5323(–06) 4.00 1.1212(–06)4.00 81 /8, 1/8)4.4908( 7.0682(3.99 1111 (10,10) 9.6530(–03) 1.2891(–02) 1.4054(–02) 3.6026(–02) 1.6494(–02) 2121 (5,5) 4.6367(–03) 1.06 4.9883(–03)1.37 5.0340(–03)1.48 1.1336(–02) 1.67 6.8089(–03)1.28 2.29 9.5928(–04)2.38 8.1280(–04)2.63 2.0086(–03) 2.503281(–03)2.36 8181 (5/4, 5/4) 9.0223(–05) 3.39 9.0385(–05)3.40 100,100) 5.7441(–02) 1.8322(–02) 2121 (50,50) 1.0511(–02) 2.45 1.0879(–02)0.75 292(– 4141 (25,25) 6.6370(–04) 3.99 5.8353(–03)90 (25/2, 25/2) 1.(–03)1.12 161161 (25/4, 25/4) 8.5244) 0.99 9.6240(–04)1.48 321321 (25/8, 25/8) 2.0814(–04) 2.03 2.1228(–04)2.18 81 (1 5.5187(–08) 3.99 5.5187(–08)3.99 –08)3.99 9.6631(–08) 3.99 –08) 2 10 4141 (5/2, 5 /2 ) 9.4892(–04) 1. 6.9922(–05)3.54 1.8443(–04) 3.45 1.2511(–04)3.41 1.9735(–02) 2.7883(–01) 2.2093(–02) 1.1782(–02)0.74 8.8185(–02) –1.66 1.302)0.73 1111 ( 3 10 0.6.3558(–03)0.89 2.7366(–02) 1.69 7.2365(–03)0.88 2.9415(–03)1.11 8.1345(–03) 1.75 3.4111(–03)1.08 8181 6570(–0 3) –1.32 2.6765 6(–0 1.0164(–03)1.53 2.2469(–03) 1.86 1.2841(–03)1.41 1.8988(–04)2.42 4.4575(–04) 2.33 2.9124(–04)2.14 4. Conclusions e have deveteristics risons for echemes. The characteristic comparisons are also been extended for two dimension this short analysis that when exponential compact higher order schemes reeving the sourc term as a linear combination of its values at the sur ounodatriv tivter to use or so that te resultant schem and he uth same reason, the fourth order ECHO schemes developed in isretisting scheme [2,3]. The same is also true when the ECHO schemes are extended r 2D CDE, the copondi three prameter schemes are comparatively less efficient than the four or six parameter based schemes. ish and Industrial Research for the financial support 09/084(0389)/2006-EMR-I. 6. References [1] E. C. Gartland, Jr., “Uniform High-Order Difference es r artuedBoundary Value Problem,” Mathematics of Computation, Vol. 48, 787. doi:10.1090/S0025-5718-1987-0878690-0 In this work wloped and made charac based compaxponential compact s al problems. It can be concluded from a gnerated by ealuate rndig nl poins and its deaes, it is bet nparam h eters to generate an e will have a bet th nder schem ter resolution e nce canproduce more accurate soltions. For e th wok ar more accurate than he exs fo rresnga 5. Acknowledgements Author Nachiketa Mra is greatly indebted to the ouncil of ScientificC Schemfo Singularly Perb Two-Point No. 1, 198, pp. 551-564 lrxinif- ference Methods for Boundary Value Problems of Con- e sitenor Nume- rical Methods in Fluids, Vol. 37, No. 1, 2001, pp. 87-106. /fld.167 [2] A. C.R. Pil ai, “Fourth-Oder Eponential Fite D vectiv Di ffuon Type,” Inrnatioal Journal f doi:10.1002 [3] Z. F. Tian and S. Q. Dai, “High-Order Compact Expo- nential Finite Difference Methods for Convection-Di- Copyright © 2011 SciRes. AJCM  S.V.S.S. YEDIDA ET AL. 54 ffusion Typef Computa sV22 2-9. doi:10.1016/j.jcp.2006.06.001 Problems,” 0, No. 2,Journal o 2007, pp. 95tional Phy- ics, ol. 74 [4] . . Sas Slu tioned er Order Sch CSr tite Methods in Apo 1 N14 doi:10.1016/j.cma.2008.06.013 Y. VS. Snyasiraju and N. Mihra, “pectral Reso- Exponen HO) fotial Compact Hi Convectigh on-Diffusion eme (SRE- on,” CompuEqua r plied M -52, 2008,echanics and Engineering pp. 4737-47, Vl. 97, o. 54. [5] M. Ilin, “A Difference Scheme for a Differential Equationlying tematiches i, Vol. 6, , 19, pp udUnsteady ciat oa- , .1 .j0 A. ' with a Small Parameter Multip the Highest Derivative (Rus No. 2sian),” Ma . 237-248. kie Zametk 69 [6] D. Yo Conve , “A H tion-D igh-Order Pa ffusion Equé ADI Method for ions,” Journal of C mput tional PhysicsVol. 214, No. 1, cp.2005.10.0 2006, pp 1. 1-11. doi:10 016/j [7] S. K. Spectra L“itfmth l-Like Resolution” Physics, Vol. 103, No. 1, 1992, pp. 16-42. doi:10.1016/0021-9991(92)90324-R ele, Compact Fin ,e Dif Journal of Computational erence Schees wi Copyright © 2011 SciRes. AJCM |

