 Journal of Power and Energy Engineering, 2015, 3, 262-268 Published Online April 2015 in SciRes. http://www.scirp.org/journal/jpee http://dx.doi.org/10.4236/jpee.2015.34035 How to cite this paper: Peng, J.C., Zhou, J. and Jiang, H. (2015) A Liability Division Method for Harmonic Pollution Based on Line-Transferred Power Components. Journal of Power and Energy Engineering, 3, 262-268. http://dx.doi.org/10.4236/jpee.2015.34035 A Liability Division Method for Harmonic Pollution Based on Line-Transferred Power Components Jianchun Peng*, Jun Zhou, Hui Jiang College of Mechatronics and Control Engineering, Shenzhen Univer si ty , Shenzhen, China Email: *jcpeng@szu.edu.cn Received February 2015 Abstract The existing l iability d ivis ion me th ods f or h armonic pollution are either inexp licit or incompl ete in physic al mea ning. To comp ensate th ese d efects , two new method s are p roposed b ased on line-transferred p ower co mponen ts in this p ap er. At first , al l h armo nic sou rces are rep resented by ideal equ ivalent curr ent s ou rce, line cur ren t c ompo nents an d bu s vol tag e c omp onents of a source are determ ined by stimul ati on of this s ou rce with all other sou rces d isabled . Then, the line -tr an s- ferred po wer comp onen t owin g to a source under all sou rce s act i on tog ethe r is determi ned by the theor y of line-tra nsferr ed power compo nents, and called source’s line-transferred power compo- nent. At last , th e li abili ty of a sourc e f or line-end h armonic pollution is divided by t wo meth ods: the r ati on of th e s ou rce ’s line-transfe rred ac tive powe r comp onent to the to tal l ine-t ransfe rred power, and the ratio n of projection of the source’s line-tran sfe rred complex power compon ent to absolute value of the total line-transferred complex power. These two metho d s are taken into ac- count no t only h ar mon i c v ol tage but als o ha rmonic c u rren t in the li abili ty di vision. Simulation re- sults show tha t the pr oposed liability division meth od based on active power c ompon ent is the most eff ective and id e al one. Keywords Harmonic Pollution, Liability Division, Line-T r ansfer red Powe r, P ow er C ompon ent, Grid 1. Introduction With the developme nt of mode rn indust ry and the use of a large number of power electro nic devices, the har- monic sources have been increasing in p ower networ k. They seriously influence the no rmal wo rk of sensitive loads and precision devices in the grid [1]-[4]. For the power quality pollution caused by harmo ni c waves, a mana gement sc heme of reward s and punishments is suggested in [5]. Therefore, a comprehensive, reasonable and quantitative liability division method of a source for harmonic pollution is crucial under the coexistence of several harmonic sources. *Corresponding author.  J. C. Peng et al. Cons i der i ng t he volt age sensi tivity of electrical equipment, many researchers proposed a liability division met hod for harmonic pollution based on harmonic voltage. A non-invasive liability division met hod was pro- posed in [6] for ha rmo ni c pollutio n based on the fa st compone nt s of harmo ni c cur rent injected by harmonic sources and the statistical features of indep endent rand om vectors. A liability division method was proposed in [7] for assessi ng harmonic pollution based on the improvement of traditional least squares method and M-esti- mation robust regres si on. It overcomes the d i sadvanta ges of the traditional least squares method, such as the lo w accuracy, sensiti vit y to singular data. A liabilit y divisio n method was proposed in [8] for q ua ntify the har monic pollution, wh ich is based on the estimated harmonic impedance and b ack ground harmonic volt a ge using com- plex least squares method. It overcomes the short a ge of the linear re gr ess ion metho d by using the real and im- aginary components respectively to estimate the harmo ni c i mpedance and quantify the har moni c liability. The re are some other researchers proposing a liability division method fo r harmonic po llution based on har- monic currents. A liability divisio n me thod was proposed in [9] for harmonic pollutio n from the perspective of harmonic c urrents based on QR-RLS ( Recursive Least-Squar e s Method based on QR decomposition). A liabilit y division method was proposed in [10] for harmonic pollut io n, whic h apportions the voltage and curr ent harmon- ic step by step considering the filter, initial p hase angles of har monic voltage and cur rent as well as the number of harmonic so ur c e s. In addition, from the viewpoint of harmonic p ower, a qualit a tive liabil it y division method for harmonic pollu- tion was proposed in [11]. The method evaluated the liabilit y of each harmoni c sour c e qualitative l y according to the power r e sp onse produced by the actio n alone of this source. Compared to the har monic voltage or har monic curr ent based meth od in which the V and I characteristics are not invol ved completely, t h is qualitative liabilit y division me thod co mpensates this drawback. However, it is a challenging problem that how to quantitati vel y di- vide the harmonic po llution lia bility among sources based on harmo nic power, because the power does not meet the superposition the orem. The electrical characteristics of harmonics are reflected by not only the volt age (or electric field) but also t he curr ent (or magnetic field). It is the power (there is no any other qua nt i ty) that invol ves both of them (vol t a ge and current). So only the q uan titative l iab ilit y division method for harmonic pollutio n based on harmonic power is the most complete and explicit one. In this paper, e mployi ng o ur achievements, two q u antitati ve liabilit y divi- sion methods for harmo ni c po llution based on the ha rmonic power are proposed. Simulation and anal ysi s show that the quantitat ive liab ilit y division me thod for harmonic po llution based on line-transferred active power component is the most desirable o ne . 2. Concept of Har monic Po llu tio n Liabil ity In a power gri d, there ofte n coexist several harmonic sources. Fig ure 1 sh ows a point of common coupling (PCC) connected to several lines. The harmonic voltage and current as well as complex power o verline end- , denoted by , and , are respo nse s under all harmonic sources action together . T he level of harmoni c pollution liabilit y of a source should be decided by the ration of the sou rce’s component contrib ution to t he sum of component contributions over a ll sour c e s. For a harmonic wave o ve r line end- (or the PCC), the liability of a source for harmonic pollution is defined as the ration of the source’s line -transferred compo nent con trib ution to the sum of compone nt contributio ns over all sources, and br iefly called thi s source’s harmonic p o llutio n liability. Electrical quantities representing harmonics are harmonic c urrent, volt age and power. Currently, there are onl y two q ua ntita tive l iab ilit y division methods for harmonic pollution, one is based on har moni c cur rent and the other is based on harmo ni c volta ge. As s ume that there are n harmonic sources in a grid. For line end- , a source’s harmo ni c pollutio n li ab ilit y based on harmo ni c volt age is calculated by Fig ure 1. A PCC connected to several lines.  J. C. Peng et al. . (1) is the harmonic pollutio n liab ilit y of source-k over line end- . is the projection of phasor (response of harmonic voltage c ompone nt over line end- under sour ce-k action alone) on phasor (total re sponse of harmonic volt age over line end- ). A source’s harmonic po llu tion liab ilit y based on harmonic curr ent is calculated by . (2) is the har monic po llu tion lia b ilit y of source-k over line end- . is the projection of phasor (re- sponse of har monic curre nt compone nt o ver line end- under source-k action alone) on phasor (total re- sponse of har monic c urre nt o v er line end - ). As the voltage is an important power qualit y index, the research of voltage-based liability division method for harmonic po llution is relati ve l y deeper than that of current-based one. The level of harmonic vo l t age (current) will increase sharply when series (p ar alle l) harmonic impedances mat ch in a grid. So the harmoni c vo ltage- or curr ent-based method can’t reflect completely t he electrical characteristics of harmo ni cs. In addition, the calcu- lation of voltage - or current-based harmonic po llut ion liability needs the projec tion of component on the total, whi ch ma kes no t only the ph ysical meaning inexplic it but also the dive rge nce in the level of harmonic pollution liabilities big [12]. Thus, it wo u ld be more complete and reasonable to take into account both harmonic voltage and current , or take into account harmonic power, in determining har monic po llutio n liabil ity. However, the re is no power-based qua ntitat ive liab ilit y divisio n meth od fo r harmonic pollution till now. Thi s is because “power does not meet the superposition theorem”. In this paper, employing our achievements, t wo liabilit y division me- thods for ha rmonic po llut ion based on harmonic power are proposed. 3. Liabil ity D ivis ion M ethod for Ha r m o n i c Pollution Based on Power 3.1. Theory of Line-Transferred Power Component By circuit theory, p ower does not meet the superposition theore m. In order to quantitatively divide the harmo ni c pollution liabilit y a mong so urces based on power, source-k-driven line-transferred complex power compo nent under coexistence of all harmonic sources must be determined at fir st. A formula for determining source-k-driven line-transferred complex power component is derived and proved in [13] [14] based on the additive, effe ct ive- ness and symme t ry, wh ich complies wi th t he circuit l aws wit hout any assumptio n. 11 0.5 0.5 nn kkk kk kk S VIIV ∗∗ ′′′ ′′ = = = + ∑∑ . (3) is the so urce-k-driven line-e nd- -transferred complex power component. and are the real and imagina ry parts of . is the conjugatio n of . Obviously, the sum of line-end- - transferred complex power components over all so urces is equal to the total complex powe r ove r line-end - . . (4) is the total complex power over line -end- under all sources action together . and ′ are the real and imagi nar y parts of . With formul a (3), the ha rmonic po llution liab il it y can be quantitativel y divid ed among harmo nic sources based on power. 3.2. Liability Division Method for Harmonic Pollution Based on Line-Trans f e rre d Active Power Component The active power is the physical quantity really reflecting the capability of power transmission in a grid, while the reactive power is just the amplitude of the power travelling back and forth in the grid. A source’s harmonic po l l u- tion liability based on line-transfer red active power component can be determined by the following fo rmul a. 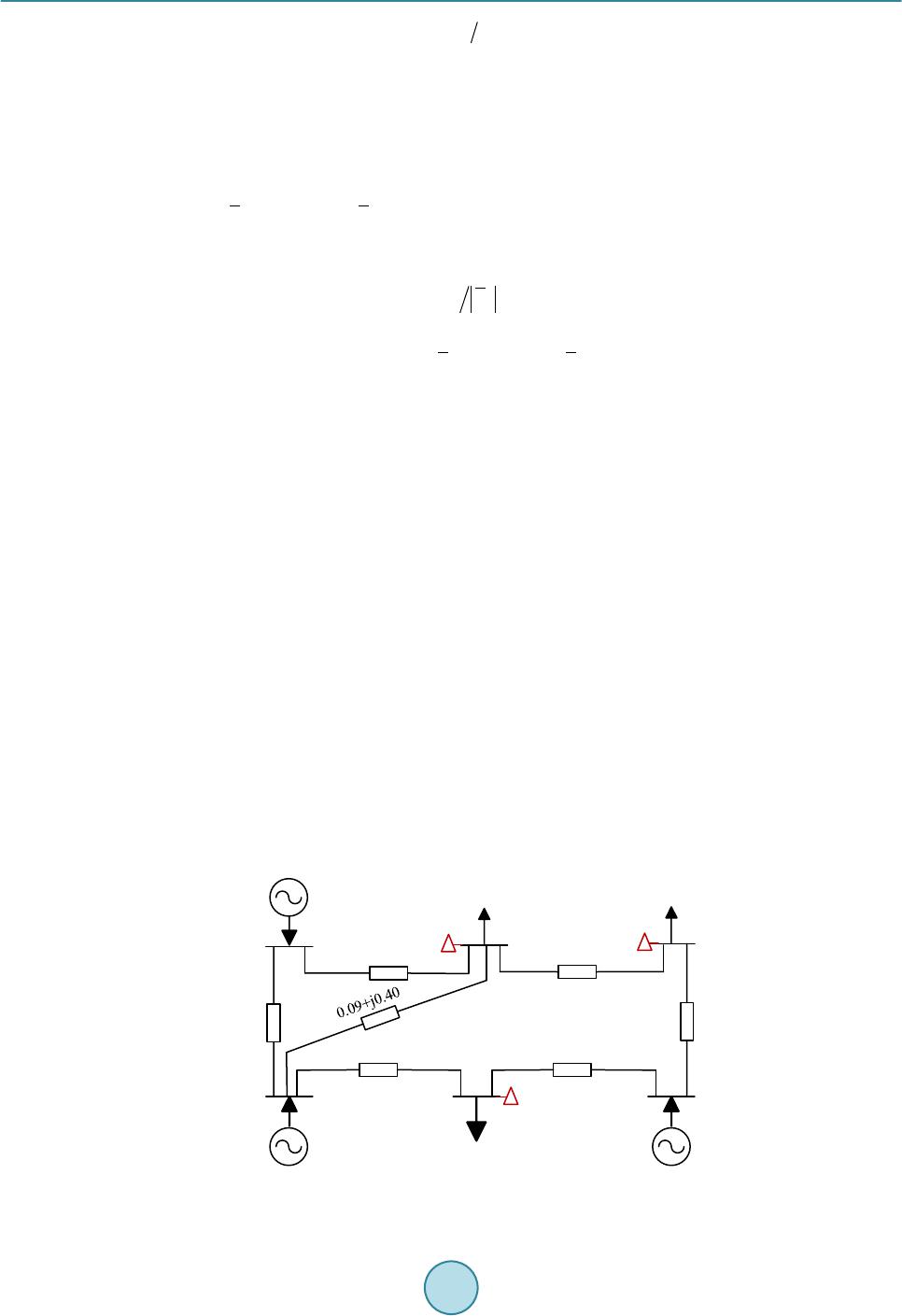 J. C. Peng et al. . (5) is the harmo ni c p o llution li ab ilit y of source-k ove r line end- based on line-transferred active power component. 3.3. Liability Division Method for Harmonic Pollution Based on Line-Trans f e rre d Complex Power Component Similar to the quantitative liabili ty division metho ds for harmonic pollutio n ba se d on voltage or c ur re nt , the projection of phasor on phasor can be used to quantitatively divide the harmonic po llut ion lia bil- ity of sour ce-k over line end - . As a res ul t , a source’s harmonic pollutio n liab ilit y ba sed on line-transferred complex powe r component can be determined by . (6) is the harmonic pollution liability of sourc e-k ove r l i ne e nd - based on line -transferred complex pow- er component. is the proj ec tio n of phaso r on phaso r . 4. Case Study The two ne wl y proposed methods for qua ntit ativ e div isio n of har mo ni c pol lutio n liability, represented by (5) and (6), are based on line-transferred ac ti ve -a nd complex -power components, and called P-method and S- method, respectively. A ca se st ud y is performed to show the effectiveness of the two methods. And the simulation res ult s by the volt a ge - and current-based methods (respectively called V-method and I-method) are also given for compariso n. The IEEE 6-bus system shown in Figu re 2 is used for t he te st. T he system contains thre e ge ne r at o r s, six bus, and seven transmi ssio n lin es. Li ne impeda nces (in p.u.) at rated fre q ue ncy are also s hown in the fig ur e. Assume tha t the re are three harmo ni c sour c e s (their freq uenc y is 5 time s of the rated) located at busse s 2 and 3 as well as 5, and denot ed by H2 and H3 as well as H5, respectively. In the test, all har moni c so urc e s are represented by ideal eq ui vale nt cur re nt sourc e, all loads in the harmo n i c do mai n are represented by im- pedance model II as in [15]. The har mon ic curre nt s of the t hr ee har moni c so urc e s are 0.3780 + j0.2823, 0.8193 + j0.6608 and 0.9450 + j1.0318 p.u., respectively. In order to obviously sho w the features of the four harm oni c poll utio n liability division methods (P-me- thod, S-method, V-method and I-method), only the simulation result s of the six line s, 2-1, 2-3, 3-6, 4-2, 5-6, 5-4, are selec ted a nd li sted in Table 1-3. For intuitiveness, the bar graphs of one sourc e’s harmonic pollution liabilities over individual lines by different methods are sh own in Figure 3-5. Look at t he H3 ’s har mo n i c p oll ution liab ilit ies s h own in Figure 3 and Ta bl e 1: By I- method, the ran ge of the har mo ni c pol lutio n liab ili tiesi s [–58.681%, 176.646%], the b i gg es t of all. T he stand a rd de viatio n of the m Fig ure 2. The IEEE 6-bus system. Bus 1Bus 2Bus 3 Bus 4Bus 5Bus 6 Harmonic source H2 Harmonic source H3 Harmonic source H5 0.08 +j0.36 0.02 +j0.12 0.28 +j0.64 0.12 +j0.52 0.07 +j0.30 0.03 +j0.22 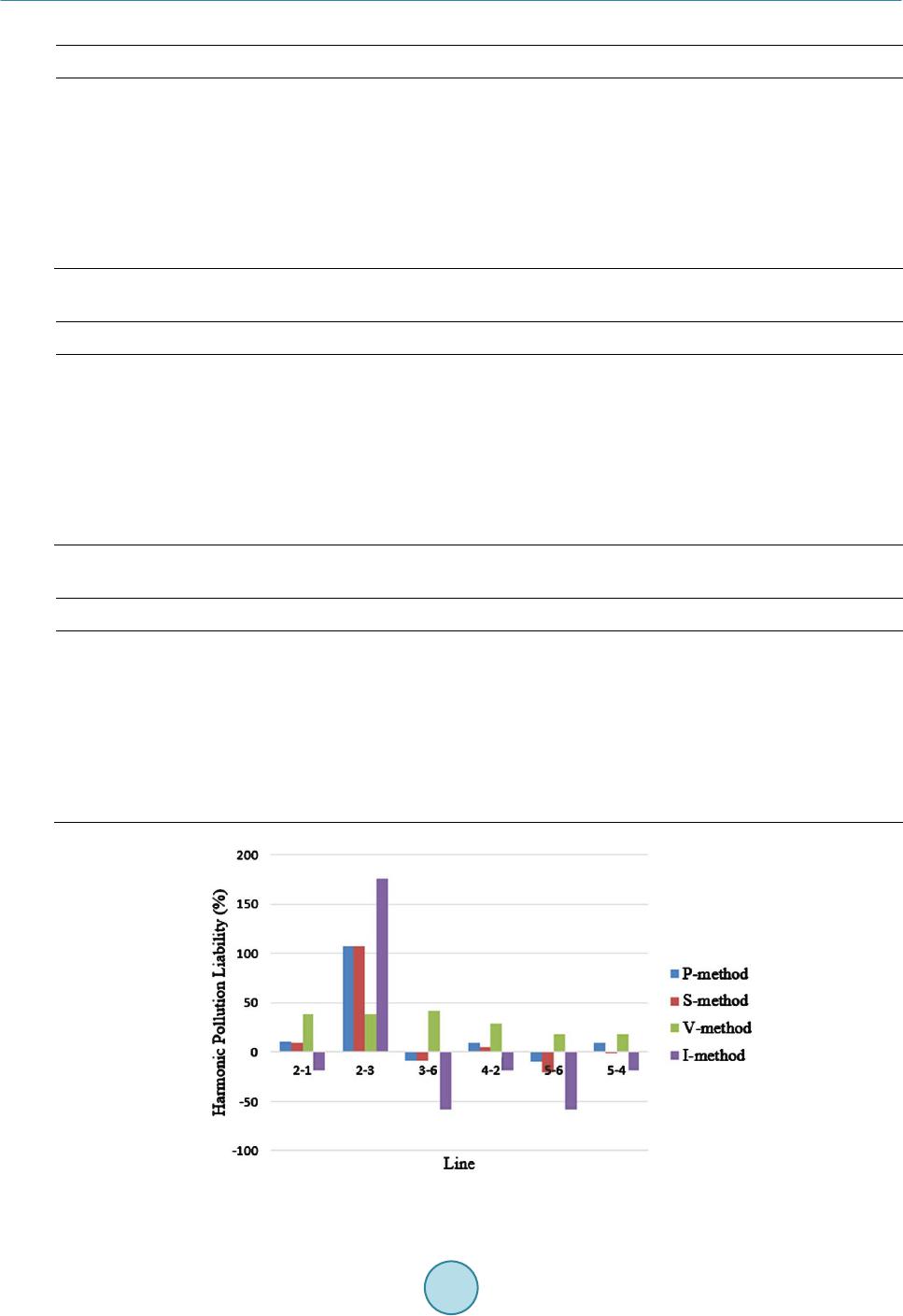 J. C. Peng et al. Table 1. Liabilities of H3 for line-end harmonic pollution by different methods. Li n e P-method (%) S-method (%) V-method (%) I-method (%) 2-1 10.158 9.672 38.150 –18.806 2-3 106.932 107.398 38.150 176.646 3-6 –8.321 –8.321 42.037 –58.681 4-2 9.744 4.805 28.415 –18.806 5-6 –10.057 –20.036 18.608 –58.681 5-4 9.545 –0.099 18.608 –18.806 Table 2. Liabilities of H2 for line-end harmonic pollution by different methods. Li n e P-method (%) S-method (%) V-method (%) I-method (%) 2-1 0.734 0.754 18.054 –16.545 2-3 –18.810 –18.730 18.054 –55.514 3-6 4.609 4.030 16.674 –8.615 4-2 0.486 –1.377 13.791 –16.545 5-6 4.153 –0.026 8.563 –8.615 5-4 0.734 0.754 18.054 –16.545 Table 3. Liabilities of H5 for line-end harmonic pollution by different methods. Li n e P-method (%) S-method (%) V-method (%) I-method (%) 2-1 89.107 89.573 43.796 135.351 2-3 11.878 11.332 43.796 –21.132 3-6 103.712 104.292 41.288 167.296 4-2 89.770 96.572 57.794 135.351 5-6 105.904 120.063 72.829 167.296 5-4 90.088 104.090 72.829 135.351 Figure 3. Bar graphs of H3’s harmonic pollution liabilities versus lines. 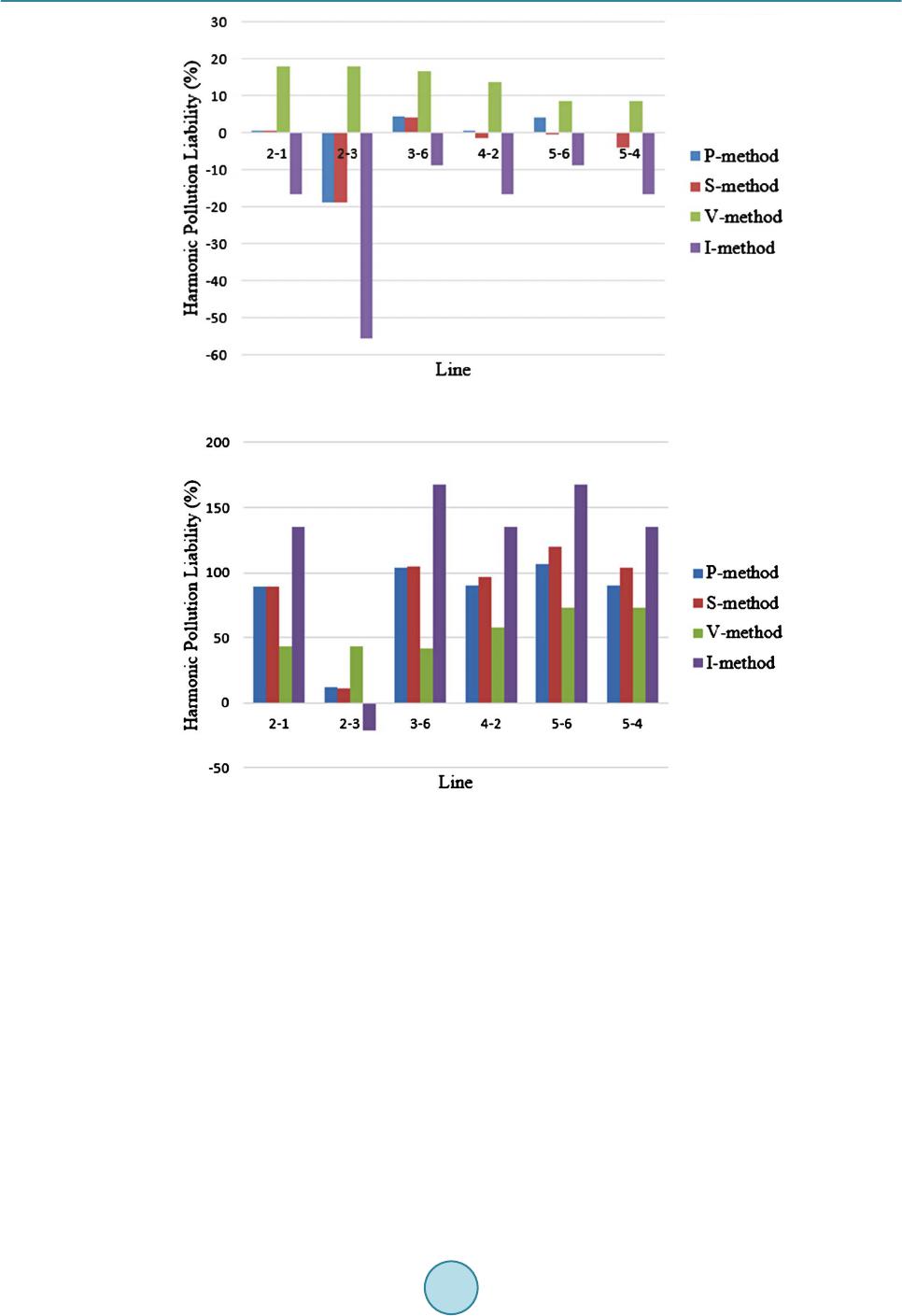 J. C. Peng et al. Figure 4. Bar graphs of H2’s harmonic pollution liabilities versus lines. Figure 5. Bar graphs of H5’s harmonic pollution liabilities versus lines. is 0.885, also the biggest of all. It indicat es that the I-method is the most unre a so na b l e and extreme method. By V-method, the ra n ge of the har monic pol lutio n liabil itie si s [18.608%, 42.037%], the smallest of all. The sta nda rd de viatio n of the m is 0.104, also the smallest of all. Thus V-method goes to a not he r extreme opposite to the I-method. By P -me tho d and S- method, the ra n ge of the har moni c pollu tio n liabi litie s are respectively [−10.057%, 106.932%] and [−20.036%, 107.398%], t he mediu m a mo n g al l. The standard deviations of them are respectively 0.437 and 0.462, also t he medi u m a mon g all. Both P- method a nd S -method are reasonable viewing fro m the ranges of thei r harmonic po llut io n liabil itie s. The real part of a complex po wer mea n s the average power delivered by the gr id , wh il e the ima ginary p art of a c o mp l e x p ower is the amplitude of powe r tr avell i ng back and fo r t h in the grid . T he ir physical meanings are quite different. In addition, the S-method needs pro jectio n of compl ex p owe r co mp o nent on total com- plex power. T he se mak e the S -method inexp licit in physical meaning. In conc l us ion, the P-method (liab ili ty division met ho d for harmo ni c poll utio n ba sed on line-transferred active power co mp o nent) is the mos t ide al met ho d, wh i ch is no t only explicit in physical meaning but also comple te a nd reasonable . For harmon ic sour c e H2 or H5, the sa me co nclu sion can be made fro m F igur e 4 and Table 2, or Fig ure 5 and Ta ble 3.  J. C. Peng et al. 5. Conclusions The range and standard deviatio n of liabilities for harmonic pollution by the c urrent-based meth od are the big- gest of all. Those by the voltage-based method are the smallest of all. The two methods go to opposite extremes and are unreasonable. The newly proposed two methods, which respectively based on line-transferred active power compo nent and line-transferred complex power component, take all factors into account (complete) and give reasonable levels of liabilities for harmoni c p o ll ution. However, the met hod based on line-transferred complex power component needs projection of the co mplex power component, thus ine xp lic it in physical meaning. As a result , the liab ili t y divisio n metho d for har monic pollution based on line-transferred active power compone nts is not only complete and explicit but also reasona- ble, and it is worth of recommendation. Funding This work is supported by National Natural Science Foundation of China under grant 51177102. References [1] Sri nivasan , K. (1996) On Separating Customer and Supply Side Harmonic Contributions. IEEE Transactions on Power Delivery, 11, 10 03-10 12. http://dx.doi.org/10.1109/61.489362 [2] Shi, L.J . and Zh ao, J.G. (2002) Application of Active Po we r Filter to Improve Powe r Quality. Proceedings of the EPSA, 14, 36-306. [3] Hu, M. and Chen, H. (2000) Sur vey of P o we r Quality and Its An a ly s i s Method. Power System Technology, 24, 36-38. [4] Gu r s oy, E. and Niebur, D. (2009) Harmonic Load Identification Using Complex Independent Component Analysis. IEEE Transactions on Power Delivery, 24, 285-292. http://dx.doi.org/10.1109/TPWRD.2008.2002968 [5] McE achern , A., Grady, W.M . an d Moncr ieff, W.A. (1995) Revenue and Harmon icsan Evaluation of Some Proposed Rate Stru ctur es. IEE E Transactions on Pow er Delivery, 10 , 123-128. http://dx.doi.org/10.1109/61.368364 [6] Hui , J., Yang, H .G. and Ye, M.Q. (20 11 ) Research on the Liability Partition of Harmonic Pollution of Multiple Har- monic Sources. Proceedings of the CSEE, 31, 48-54. [7] Sun, Y.Y. and Yin, Z.M . (2012 ) Quantifying Harmonic Responsibilities of Multiple Harmonic Sources Based on M- Estimation Robust Regression . Proceedings of the CSE E, 32, 166 -173. [8] Jia, X.F., Hua, H.C., C ao, D.S . and Zh ao , C.Y. (2013 ) Determining Harmonic Contributions Based on Complex Least Squ ares Met hod. Proceedings of the CSE E, 33, 1 49-15 5. [9] Ma, H.Z., Xu, G. , Song, S.P ., Z hao, H.F. and Ren , L.Z. (2014) Quantitative Anal y s i s of Harmonic Current Liability in Distribution Netwo rk. E clectic Po wer Automation Equipme nt, 34, 44-49. [10] Xu, J.Z. , P ang, L.Z., et al. (2012) Quantitative Ana lysis fo r Harmon ic Liability Prorat ion among Multiple Harmonic Sou rces. Electric Power Automation Equipment, 32, 38-42. [11] Ye, J. (2010) A Liability Sharing Meth od Bas ed on Harmonic Powe r . Journal of Electric Power , 25, 2 10-21 3. [12] Hua, H.C., Jia, X.F., Cao, D.S. and Zhao , C.Y. (2013) Harmonic Contribution Estimation under Po wer Qualit y Data Interch ange F ormat. P ower S ystem Technology, 37, 3110-3117. [13] P eng, J.C. (2005) Definitions of Branch’s Originating Po we r Component and Branch’s Dri ven Po wer Component and Thei r Analysis. P ower Sys tem Technology, 29, 24-29. [14] P eng, J.C., Zeng, Y.G. and Jian g, H. (2012) Resolution of Line-Transferred Po we r in Gr i ds Yielded by Circuit-Laws ’ Symmetry under Deducti ve Reasoning of Shapley Theorem. IET Generati on, Transmission & Distribution, 6, 627- 635. http://dx.doi.org/10.1049/iet-gtd.2 01 1.05 36 [15] Burch, R., Chang, G., Hatzi adoniu, C. , et al. (2003) Impact of Aggregate Linear Load Modeling on Harmonic An a lysis: A Comparison of Common Practice an d Anal ytical Models. IEEE Transactions on Power System, 18 , 625-63 0. http://dx.doi.org/10.1109/TPWRD.2003.810492
|