Intelligent Control and Automation, 2011, 2, 69-76
doi:10.4236/ica.2011.22008 Published Online May 2011 (http://www.SciRP.org/journal/ica)
PID Parameters Optimization Using Genetic Algorithm
Technique for Electrohydraulic Servo Control System
Ayman A. Aly
Mechatronics Section, Faculty of Engineering, Assiut University, Assiut, Egypt
Mechatronics Section, Faculty of Engineering, Taif University, Taif, Saudi Arabia
Received January 16, 2011; revised March 21, 2011; accepted March 26, 2011
Abstract
Electrohydraulic servosystem have been used in industry in a wide number of applications. Its dynamics are
highly nonlinear and also have large extent of model uncertainties and external disturbances. In order to in-
crease the reliability, controllability and utilizing the superior speed of response achievable from electrohy-
draulic systems, further research is required to develop a control software has the ability of overcoming the
problems of system nonlinearities. In This paper, a Proportional Integral Derivative (PID) controller is de-
signed and attached to electrohydraulic servo actuator system to control its angular position. The PID pa-
rameters are optimized by the Genetic Algorithm (GA). The controller is verified on the state space model of
servovalve attached to a rotary actuator by SIMULINK program. The appropriate specifications of the GA
for the rotary position control of an actuator system are presented. It is found that the optimal values of the
feedback gains can be obtained within 10 generations, which corresponds to about 200 experiments. A new
fitness function was implemented to optimize the feedback gains and its efficiency was verified for control
such nonlinear servosystem.
Keywords: Optimal Control, PID, GA, Electrohydraulic, Servosystem
1. Introduction
Electrohydraulic servosystems are widely used in many
industrial applications because of their high power-to-
weight ratio, high stiffness, and high payload capability,
and at the same time, achieve fast responses and high
degree of both accuracy and performance [1,2]. However,
the dynamic behavior of these systems is highly nonlin-
ear due to phenomena such as nonlinear servovalve
flow-pressure characteristics, variations in trapped fluid
volumes and associated stiffness, which, in turn, cause
difficulties in the control of such systems.
Control techniques used to compensate the nonlinear
behavior of hydraulic systems include adaptive control,
sliding mode control and feedback linearization. Adap-
tive control techniques have been proposed by research-
ers assuming linearized system models. These controllers
have the ability to cope with small changes in system
parameters such as valve flow coefficients, the fluid bulk
modulus, and variable loading. However, there is no
guarantee that the linear adaptive controllers will remain
globally stable in the presence of large changes in the
system parameters, as was demonstrated experimentally
by Bobrow and Lum [3]. Variations of sliding mode
controllers have also been developed for electrohydraulic
servosystems. These controllers are robust to large pa-
rameter variations, but the nearly discontinuous control
signal excites unmodeled system dynamics and degrades
system performance. This can be reduced by smoothing
the control discontinuity in a small boundary layer bor-
dering the sliding manifold as introduced in simulations
[4,5]. The nonlinear nature of the system behavior re-
sulting from valve flow characteristics and actuator
nonlinearities have been taken into account in application
of the feedback linearization technique [6]. The main
drawback of the resulting linearizable control law is that
it relies on exact cancellation of the nonlinear terms.
A. Aly [7] presented a nonlinear mathematical model
which allows studying and analysis of the dynamic
characteristic of an electrohydraulic position control
servo. Response for the angular displacement of motor
shaft due to large amplitude step input were obtained by
applying velocity feedback control strategy. To improve
the dynamics response characteristics and based on the

A. A. ALY 70
mathematical model driven, the implementation of self
tuning fuzzy logic controller (STFLC) technique was
investigated in [8] for positioning the servo motor system
as a nonlinear plant. Feasibility and robustness of such
application was assured. However, it is still extremely
difficult to establish a systematic standard design method
for fuzzy logic control system like PID controller which
is forward linear differential equation.
Over the past a few years, many different techniques
have been developed to acquire the optimum control
parameters for PID controllers. The academic control
community has developed many new techniques for tun-
ing PID controllers. They have not been slow in seeking
to exploit the emerging methods based on the principles
of evolution. A GA is one such direct search optimiza-
tion technique which is based on the mechanics of natu-
ral genetics. An advantage of the GA for autotuning is
that it does not need gradient information and therefore
can operate to minimize naturally defined cost functions
without complex mathematical operations, [9].
This article describes the application of GA Technique
based on new fitness function to optimally tune the three
terms of the classical PID controller to regulate a valve
controlled hydraulic servosystem as a nonlinear process.
The paper has been organized as follows: Section 2
describes the system dynamic model. Section 3 reviews
the PID tuning methods and introduces the new tech-
niques for PID tuning method. Section 4 presents a
simulation of the system with GPID controller. Finally, a
conclusion of the proposed GPID technique is presented
in Section 5.
2. System State Space Dynamic Model
The hydraulic position control system consists of a pres-
sure compensated vane pump, a two-stage servovalve
(Moog Model 761 [10]) a servoamplifier, and a fixed
displacement hydraulic motor with an inertial load at-
tached to the motor shaft, Figure 1. A shaft encoder is
attached to the motor shaft for position measurement.
This type of hydraulic system is typically applied to
mixer drives, centrifuge drives and machine tool drives
where accurate control with fast response times is re-
quired and large changes in load can be expected.
The control signal is the voltage to the servoamplifier,
the resulting servoamplifier current actuating the ser-
vovalve. The dynamic model is developed under the fol-
lowing assumptions:
1) The supply pressure is constant.
2) Servovalve orifices are symmetrical.
3) Valve flow is modeled by turbulent flow through
sharp-edged orifices.
4) Motor external leakage is negligible.
The nonlinear dynamic equations describing the sys-
tem may then be written in a compact state-space form,
the control input being the voltage to the servoamplifier.
Definitions of the state variables and inputs of the system
are given below:
States:



 
1234 L
L
x
xxxttP tPt 





 (1)
Inputs:




12 is
uuV tP



 (2)
Applying the states definition to the system, after ma-
nipulation, results in the state variable model as follows:
12
x
x

, 223 2
sgn
mc
VT B
x
xx
JJJ
 
x
34
,
x
x


and
Figure 1. Electrohydraulic rotary position servosystem.

A. A. ALY71
 
 
33
41 2
22
2
34 2
33
1
2
44
sgn1sgn1sgn
444 4 1sgn
4sgn1 sgn1 sgn
hxa shm
xx
c c
hm hehehm
c
ccc c
h
xa xx
c
KKKkkxxK VB
xxVV xV
Vnuu VJ
KVK LK LKV
xx Tx
JV VVJV
Kxx
KKu VV
Vu






m

  
  




 




 

 
 
 

  


2
u
(3)
The state variables model represented by (1-3) is of
the nonlinear form:


,
x
fxu (4)
The initial conditions of the state variables are given
by:
 

 

1234
00000000xxxx  

(5)
More details in the system dynamics model and its
parameters are given in App endix A.
The objective of the controller is to keep the angular
position of the motor following a desired trajectory as
precisely as possible.
3. PID Controller Tuning
The popularity of PID controllers in industry stems from
their applicability and due to their functional simplicity
and reliability performance in a wide variety of operating
scenarios. Moreover, there is a wide conceptual under-
standing of the effect of the three terms involved
amongst non-specialist plant operators. In general, the
synthesis of PID can be described by,
 
0
d
dd
t
pI D
et
utKetKett Kt  
 (6)
where e(t) is the error, u(t) the controller output, and KP,
KI, and KD are the proportional, Integral and derivative
gains.
There is a wealth of literature on PID tuning for scalar
systems, [11-13]. Good reviews of tuning PID methods
are given in Tan et al. [14] and Cominos and Munro [15].
Among these methods are the well known Ziegler and
Nichols [16] Cohen and Coon [17]. Many researchers
have attempted to use advanced control techniques such
as optimal control to restrict the structure of these con-
trollers to PID type.
Recently, Hao et al. [18] have illustrated a simple ap-
proach for PID control of select the parameters of single
neutron adaptive PID controller designing. Using adap-
tive PID controller based on neuron optimization, they
show that the genetic optimize algorithm can get better
control characteristics.
3.1. GPID Tuning Strategy
Genetic programming (Koza, et al. [19]; Koza, et al. [20]
and Reeves [21]) is an automated method for solving
problems. Specifically, genetic programming progres-
sively breeds a population of computer programs over a
series of generations. Genetic programming is a prob-
abilistic algorithm that searches the space of composi-
tions of the available functions and terminals under the
guidance of a fitness measure. Genetic programming
starts with a primordial ooze of thousands of randomly
created computer programs and uses the Darwinian prin-
ciple of natural selection, recombination (crossover),
mutation, gene duplication, gene deletion, and certain
mechanisms of developmental biology to breed an im-
proved population over a series of many generations.
Genetic programming breeds computer programs to
solve problems by executing the following three steps:
1) Generate an initial population of compositions of
the functions and terminals of the problem.
2) Iteratively perform the following substeps (referred
to herein as a generation) on the population of programs
until the termination criterion has been satisfied:
a) Execute each program in the population and assign
a fitness value using the fitness measure.
b) Create a new population of programs by applying
the following operations. The operations are applied to
program selected from the population with a probability
based on fitness (with reselection allowed).
 Reproduction: Copy the selected program to the new
population. The reproduction process can be subdi-
vided into two subprocesses: Fitness Evaluation and
Selection. The fitness function is what drives the
evolutionary process and its purpose is to determine
how well a string (individual) solves the problem, al-
lowing for the assessment of the relative performance
of each population member.
 Crossover: Create a new offspring program for the
new population by recombining randomly chosen
parts of two selected programs. Reproduction may
proceed in three steps as follows: 1) two newly re-
produced strings are randomly selected from a Mat-
ing Pool; 2) a number of crossover positions along

A. A. ALY 72
each string are uniformly selected at random and 3)
two new strings are created and copied to the next
generation by swapping string characters between the
crossover positions defined before.
 Mutation: Create one new offspring program for the
new population by randomly mutating a randomly
chosen part of the selected program.
 Architecture-altering operations: Select an architec-
ture-altering operation from the available repertoire
of such operations and create one new offspring pro-
gram for the new population by applying the selected
architecture-altering operation to the selected program.
3) Designate the individual program that is identified
by result designation (e.g., the best-so far individual) as
the result of the run of genetic programming. This result
may be a solution (or an approximate solution) to the
problem. The specification of the designed GA technique
is shown in Table 1.
Figure 2 shows the flowchart of the parameter opti-
mizing procedure using GA. For details of genetic op-
erators and each block in the flowchart, one may consult
literature [22].
3.2. Fitness Measure
The fitness measure is a mathematical implementation of
the problem’s high level requirements. That is, our fit-
ness measure attempts to optimize for the integral of the
time absolute error (ITAE) for a step input and also to
optimize for maximum sensitivity.
Figure 3 shows the block diagram for adjusting the
PID parameters via GA on line with the SIMULINK
model. To begin with, the GA should be provided with a
population of PID sets. The initial population for choos-
ing PID parameters are derived from the trial-and-error
Figure 2. The optimization flowchart of GA technique.
Figure 3. Block diagram of electrohydraulic servo motor to adjust PID parameters via GA online.

A. A. ALY 73
Table 1. Specification of the GA.
Population Size 20
Crossover Rate 0.7
Mutation Rate 0.05
Chromosome Length 12
Precision of Variables 3
Generation Gap 1
method where, KP = 1.2560, K
I = 0.0062 and K D =
0.0275. A fitness evaluation function is needed to calcu-
late the overall responses for each of the sets of PID val-
ues and from the responses generates a fitness value for
each set of individuals expressed by:
 
0d
t
f
te ttt (7)
Here the goal is to find a set of PID parameters that
will give a minimum fitness value over the period [0,t].
When this cycle is completed, are produced new sets of
PID values which ideally will be at the fitness level
higher than the initial population of PID values. These
new fitter sets of PID values are then passed to the fit-
ness evaluation function again where the above-mentioned
process is repeated. This way the process is cycled un-
ceasingly until the best fitness is achieved. If the prede-
fined termination criterion is not met, again a new popu-
lation is obtained using various operators that would
have better gene. The termination criterion may be for-
mulated as the magnitude of difference between index
value of previous generation and present generation be-
coming less than a prespecified value. The process con-
tinues till the termination criterion is fulfilled.
4. Simulation of the System with GPID
Controller
The closed loop control system was solved using nu-
merical integration technique of Runge-Kutta method
with sampling time of 0.001 s. The simulation method
combines SIMULINK module and M functions where,
the main program is realized in SIMULINK and the op-
timized PID controller is predicted using M function.
Figure 4 shows the step responses of the rotary actua-
tor obtained by using the optimized feedback. The opti-
mal gains of PID controller are calculated to minimize
the fitness function which was described in (7). There-
fore some oscillations or offset in the transient response
may be shown with the implemented PID control pa-
rameters. In order to reduce steady state error and oscil-
lations in the transient response, the fitness function must
be modified in order to include steady state error and the
Figure 4. The optimized motor shaft position of different
fitness function.
oscillations in the transient response. The modified fit-
ness function is given by:
 
0
d
t
p
ss
f
ttettM e


 (8)
where α and β are weighting factors equal to 1.5 and 5
respectively, imposed by the user to achieve desired re-
sponse characteristics; Mp is the overshoot and ess is the
steady-state error. The optimized PID parameters results
at the assumed population of 20 are: KP = 1.438, K
I =
0.053 and K
D = 0.537. At the same time, the nonlinear
characteristics of the hydraulic motor and the hydraulic
pump are also the reasons of steady state error and oscil-
lations in the transient response. The settling time of the
modified fitness function is significantly shorter than that
achieved by the ITAE schemes.
The fitness distribution is computed by (8) and the
plots in the KP, KI and KD ranges are shown in Figures 5
and 6, respectively. From the fitness distribution with
respect to the number of generation plot, we can see that
the near optimal values of feedback gains can obtain with
in 10 generations, which corresponds to about 200 ex-
periments. More than this number of experiments would
be needed for manual tuning by an experienced techni-
cian. The optimal values of feedback gains are clearly
defined in a given gain space. These figures also indicate
that it would be very hard to determine optimal gains by
manual tuning, because of the contrast behaviors of the
controller parameters.
One of the important properties of any controller tun-
ing method is its robustness to model errors. As a change
in dynamics of the hydraulic servo systems, when the
motor displacement is varied, the position responses also
varied as shown in Figure 7. So that re-tuning of feed-
back gains must be carried out to obtain the desired con-
trol performance. However, the system remains stable in
the presence of these changes.

A. A. ALY 74
Figure 5. Fitness values with respect to the number of gen-
eration.
Figure 6. PID gains distribution with respect to the number
of generation.
Figure 7. The optimized motor shaft position of different
Motor displacement.
Figure 8(a) shows the ability of the system to track
the a rectangle reference input with steady state error of
0.0027 rad., rise time of 0.115 s., and zero overshooting
while, Figure 8(b) illustrates the controller signal ach-
ieved by the proposed design technique and the last parts
shows that the servo valve flow rate kept under the satu-
ration limit.
In Figures 9 and 10, a different reference signals have
been used with this system and nearly similar results
being achieved each time.
(a)
(b)
(c)
Figure 8. (a) The angular motor shaft position of square
reference input; (b) GPID controller output; (c) Servovalve
flow rate.
(a)
(b)
(c)
Figure 9. (a) The angular motor shaft position of saw tooth
reference input; (b) GPID controller output; (c) Servovalve
flow rate.

A. A. ALY75
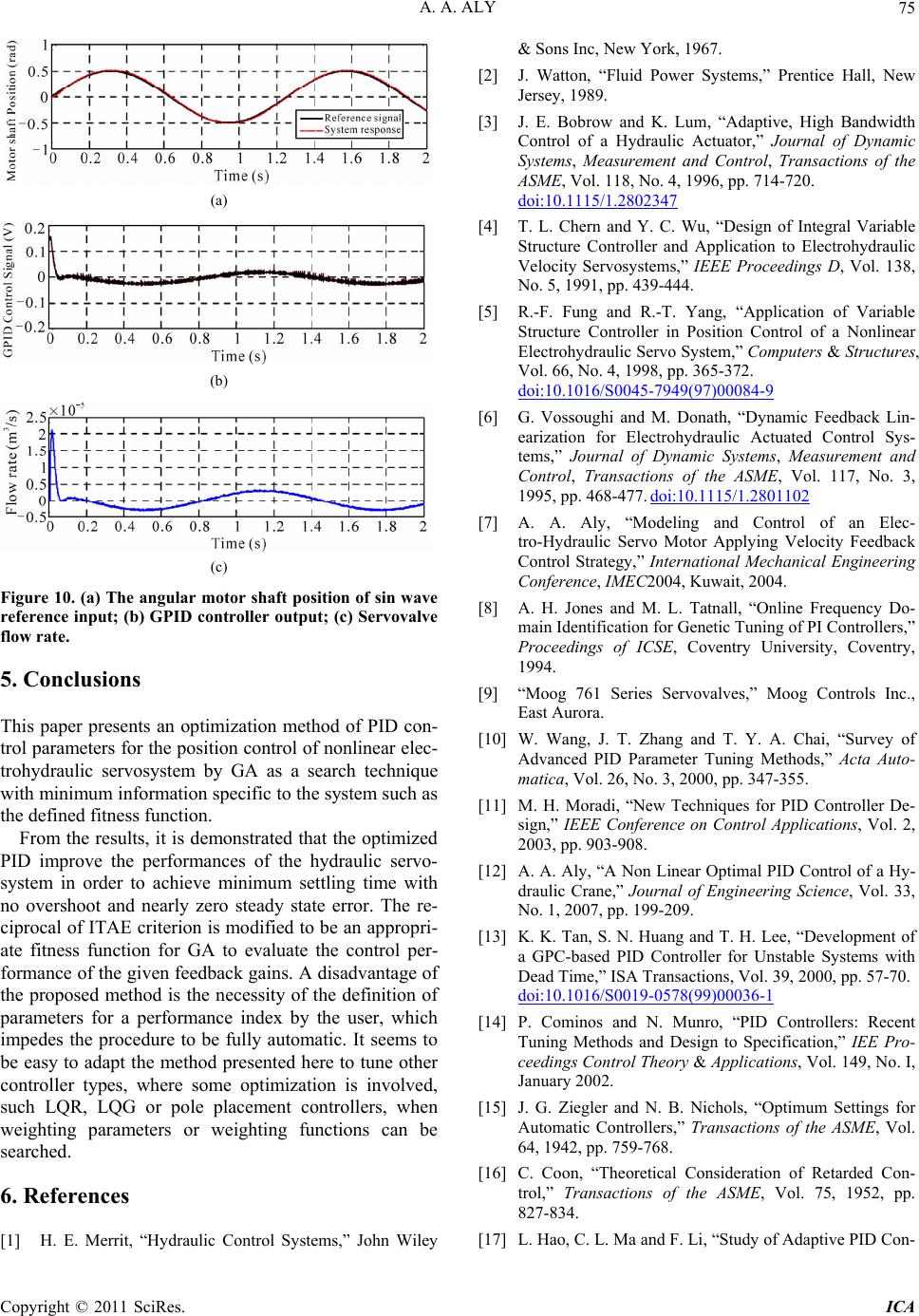
(a)
(b)
(c)
Figure 10. (a) The angular motor shaft position of sin wave
reference input; (b) GPID controller output; (c) Servovalve
flow rate.
5. Conclusions
This paper presents an optimization method of PID con-
trol parameters for the position control of nonlinear elec-
trohydraulic servosystem by GA as a search technique
with minimum information specific to the system such as
the defined fitness function.
From the results, it is demonstrated that the optimized
PID improve the performances of the hydraulic servo-
system in order to achieve minimum settling time with
no overshoot and nearly zero steady state error. The re-
ciprocal of ITAE criterion is modified to be an appropri-
ate fitness function for GA to evaluate the control per-
formance of the given feedback gains. A disadvantage of
the proposed method is the necessity of the definition of
parameters for a performance index by the user, which
impedes the procedure to be fully automatic. It seems to
be easy to adapt the method presented here to tune other
controller types, where some optimization is involved,
such LQR, LQG or pole placement controllers, when
weighting parameters or weighting functions can be
searched.
6. References
[1] H. E. Merrit, “Hydraulic Control Systems,” John Wiley
& Sons Inc, New York, 1967.
[2] J. Watton, “Fluid Power Systems,” Prentice Hall, New
Jersey, 1989.
[3] J. E. Bobrow and K. Lum, “Adaptive, High Bandwidth
Control of a Hydraulic Actuator,” Journal of Dynamic
Systems, Measurement and Control, Transactions of the
ASME, Vol. 118, No. 4, 1996, pp. 714-720.
doi:10.1115/1.2802347
[4] T. L. Chern and Y. C. Wu, “Design of Integral Variable
Structure Controller and Application to Electrohydraulic
Velocity Servosystems,” IEEE Proceedings D, Vol. 138,
No. 5, 1991, pp. 439-444.
[5] R.-F. Fung and R.-T. Yang, “Application of Variable
Structure Controller in Position Control of a Nonlinear
Electrohydraulic Servo System,” Computers & Structures,
Vol. 66, No. 4, 1998, pp. 365-372.
doi:10.1016/S0045-7949(97)00084-9
[6] G. Vossoughi and M. Donath, “Dynamic Feedback Lin-
earization for Electrohydraulic Actuated Control Sys-
tems,” Journal of Dynamic Systems, Measurement and
Control, Transactions of the ASME, Vol. 117, No. 3,
1995, pp. 468-477. doi:10.1115/1.2801102
[7] A. A. Aly, “Modeling and Control of an Elec-
tro-Hydraulic Servo Motor Applying Velocity Feedback
Control Strategy,” International Mechanical Engineering
Conference, IMEC2004, Kuwait, 2004.
[8] A. H. Jones and M. L. Tatnall, “Online Frequency Do-
main Identification for Genetic Tuning of PI Controllers,”
Proceedings of ICSE, Coventry University, Coventry,
1994.
[9] “Moog 761 Series Servovalves,” Moog Controls Inc.,
East Aurora.
[10] W. Wang, J. T. Zhang and T. Y. A. Chai, “Survey of
Advanced PID Parameter Tuning Methods,” Acta Auto-
matica, Vol. 26, No. 3, 2000, pp. 347-355.
[11] M. H. Moradi, “New Techniques for PID Controller De-
sign,” IEEE Conference on Control Applications, Vol. 2,
2003, pp. 903-908.
[12] A. A. Aly, “A Non Linear Optimal PID Control of a Hy-
draulic Crane,” Journal of Engineering Science, Vol. 33,
No. 1, 2007, pp. 199-209.
[13] K. K. Tan, S. N. Huang and T. H. Lee, “Development of
a GPC-based PID Controller for Unstable Systems with
Dead Time,” ISA Transactions, Vol. 39, 2000, pp. 57-70.
doi:10.1016/S0019-0578(99)00036-1
[14] P. Cominos and N. Munro, “PID Controllers: Recent
Tuning Methods and Design to Specification,” IEE Pro-
ceedings Control Theory & Applications, Vol. 149, No. I,
January 2002.
[15] J. G. Ziegler and N. B. Nichols, “Optimum Settings for
Automatic Controllers,” Transactions of the ASME, Vol.
64, 1942, pp. 759-768.
[16] C. Coon, “Theoretical Consideration of Retarded Con-
trol,” Transactions of the ASME, Vol. 75, 1952, pp.
827-834.
[17] L. Hao, C. L. Ma and F. Li, “Study of Adaptive PID Con-

A. A. ALY 76
troller Based on Single Neuron and Genetic Optimiza-
tion,” The 8th International Conference on Electronic
Measurement and Instruments ICEMI, Vol. 1, 2007, pp.
240-243.
[18] J. R. Koza, F. H. Bennett, A. David and K. Martin, “A
Genetic Programming III: Darwinian Invention and
Problem Solving,” Morgan Kaufmann, San Francisco,
1999.
[19] J. R. Koza, M. A. Keane, M. J. Streeter, W. Mydlowec, J.
Yu and G. Lanza, “Genetic Programming IV. Routine
Human-Competitive Machine Intelligence,” Kluwer
Academic Publishers, Dordrecht, 2003.
[20] C. R. Reeves, “Using Genetic Algorithms with Small
Populations,” Proceedings of the 5th International Con-
ference on Genetic Algorithms, 1993.
[21] D. E. Goldberg, “Genetic Algorithms in Search, Optimi-
zation and Machine Learning,” Addison-Wesley, New
York, 1989.
Appendix-A System Model and Parameters
The electrohydraulic valve consists of a first stage noz-
zle-flapper valve, and a second-stage 4-way spool valve.
The valve drive amplifier has a gain of 100 mA/V. The
model is derived on the assumption that an initially
loaded rotary motor is controlled by the electrohydraulic
servovalve. The steady-state valve model can be repre-
sented by the following relation, [4,5].
 
sgn 1sgn1sgn
L
L
xx xx
s
s
PP
QKV VV
PP

 

 (A-1)
The dynamic performance of the servovalve
sc
is de-
ribed by a first-order time lag and is given by:
d
d
x
x
QK V
t
  (A-2)
Equations (A-1, A-2) are combined to yield a dynamic
va
Q
lve model as
 
dsgn1 sgn1 sgn
d
L
L
xx xx
s
s
PP
QQKV VV
tP


 


P
(A-3)
where vx is the valve drive voltage, kx = –1.36 ×
tor is modeled by considering the
ro
10–4
m3/s/v. is the valve flow gain, and
 =2.3 × 10–3 s is the
valve time constant.
The hydraulic mo
tary motor arrangement shown in Figure 1, as well as
by taking into account oil compressibility and leakage
across the motor. Using the principal conservation of
mass yields:
d d
d4 d
CL
me
h
VP
QV LP
tKt

 
L
(A-4)
The equation of motion of the load can be given by:
2
dd 
2sgn
d d
Lm c
PV JBT
t t

 (A-5)
where vm = 0.716 × 10–6 m
3/rad is the motor displace-
(A-6)
The transport lag function is given by:
ment, vc = 20.5 × 10–6 m3 is the volume of oil in motor
and hoses, kh = 1.4 × 109 N/m2 is the hydraulic bulk
modulus, Le = 2.8 × 10–11 m5/Ns is the effective leakage
coefficient, J = 3.4 × 10–3 Nms2/rad is the inertia of ro-
tating Parts, B = 2.95 × 10–3 Nms/rad is the viscous
damping coefficient, Tf =0.225 N.M is the magnitude of
coulomb-friction, and the sign change function is defined
by:
1for 1
sgn 1for 1










0.06
s
Hse

 (A-7)
The system rotary position transducer constant, s
3.
omenclature
Viscous damping coefficient, N·m·s/rad
V
/s
cient, m5/N·s
orts, N/m
uator, m3/s
nd hoses, m3
K =
44 v/rad equipped with a 7.5 gear ratio.
N
B
Ka Operational amplifier gain
2
Kh Bulk modulus of fluid, N/m
Kx Valve flow gain at Pl = 0. m3/s/
Ks Position transducer constant, V/rad
Kθ Position feedback gain
J Load inertia, N·m·s2/rad
Le Equivalent leakage coeffi
n Reduction gear ratio
2
P1, P2 Pressures at actuator p
PL Load pressure, N/m2
Q1, Q2Inlet and outlet flow of the act
Q Mean flow rate, m3/s
Tc Coulomb -friction, N·m
Vc Volume of oil in motor a
Vi Input voltage to the system, V
Vm Motor displacement, m3/rad
Vx Valve drive voltage, V
τ Valve time constant, s
θ Shaft position, rad

 Angular frequency, rad/s