ABSTRACT

In this paper we consider the existence of a global periodic attractor for a class of infinite dimensional dissipative equations under homogeneous Dirichlet boundary conditions. It is proved that in a certain parameter, for an arbitrary timeperiodic driving force, the system has a unique periodic solution attracting any bounded set exponentially in the phase space, which implies that the system behaves exactly as a one-dimensional system. We mention, in particular, that the obtained result can be used to prove the existence of the global periodic attractor for abstract parabolic problems.

1. Introduction

In this paper, we consider a class of infinite dimensional dissipative equations with the Dirichlet boundary condition

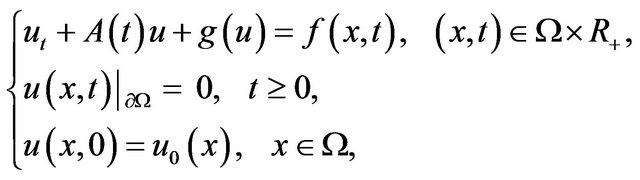(1.1)

where is a real-valued function on , is an open bounded set of 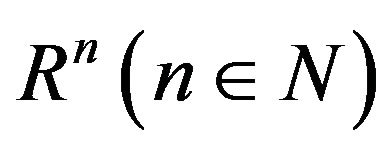with a smooth boundary, takes values in a Hilbert space H, the family of unbounded linear operators generates a linear evolution operator. The external force term is continuous and ω-periodic function in t, where ω is a positive constant. Let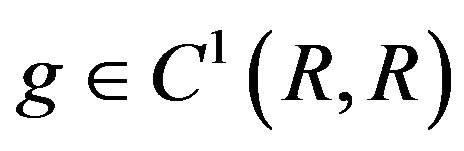. There exists a nonnegative constant, such that

(1.2)

where denotes the absolute value of the number in R.

There has been an increasing interest in the study of the evolution equations of form (1.1), such as existence and asymptotic behavior of solutions (mild solutions, strong solutions and classical solutions), and existence of global attractors, etc. Especially in physics and mechanics, many important results associated with this problem have been obtained in [1-7]. In [9] and [10], Hernandez and Henriquez have extended the problem studied in [8] to neutral equations and established the corresponding existence results of solutions and periodic solutions. In their work, , especially, is a negative Laplacian operator, and A generates an analytic semigroup so that the theory of the fractional power has been used effectively there. However, their results clearly cannot apply to Equation (1.1) with is non-autonomous which is a more general and maybe more important case [11]. So we will use the appropriate assumptions to overcome the difficulty for the non-autonomous operator.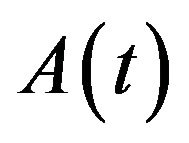

We arrange this paper as follows. Firstly we present the existence and uniqueness of solutions. Then we obtain a nonstandard estimation under which system (1.1) possesses a global periodic attractor. Finally, for the special case, we discuss the existence of a global periodic attractor for abstract parabolic problems.

2. Preliminaries

For the family of linear operators, we impose on the following restrictions:

1) The domain of is dense in Hilbert space H and independent of t, 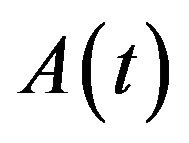is a closed linear operator;

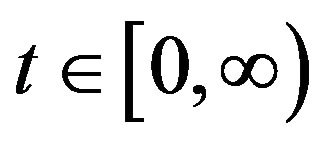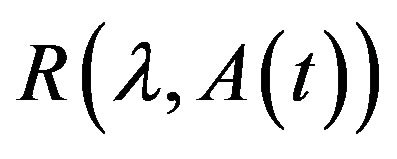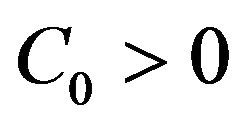2) For each, the resolvent exists for all, with and there exists so that;

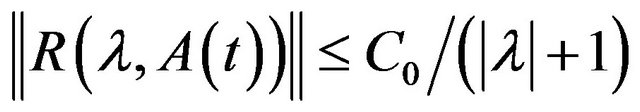3) There exists 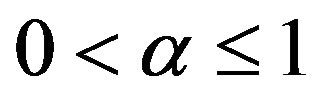and such that

for all;

4) For each and some, the resolvent set of, the resolvent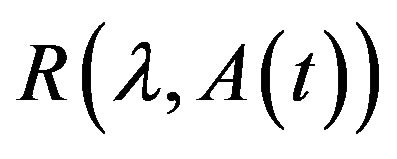, is a compact operator.

Then the family 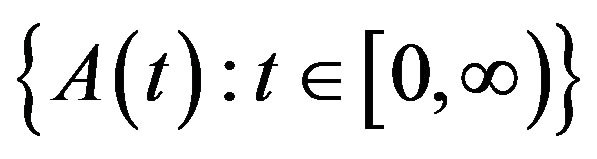generates a unique linear evolution operator, satisfying the following properties:

1)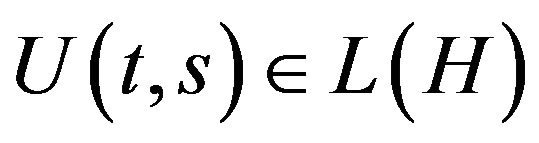, the space of bounded linear transformations on H, whenever and for each, the mapping 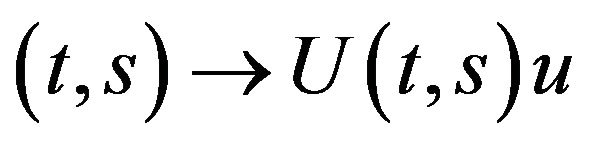is continuous;

2) for;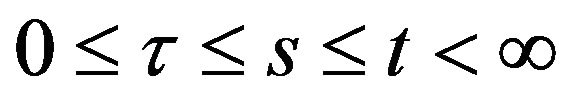

3)

4) 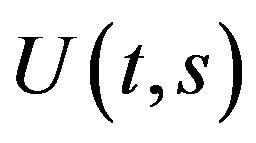is a compact operator whenever;

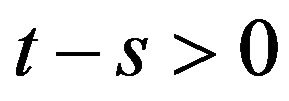5), for;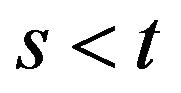

6) There is a constant 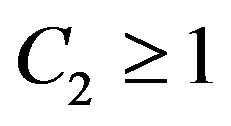such that,;

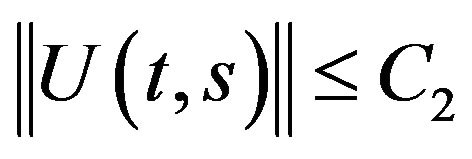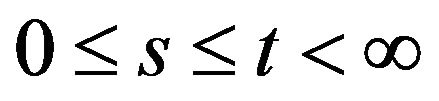7) If and then

for some;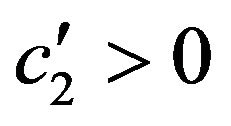

8) If 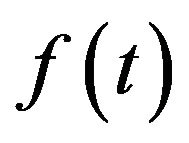is continuous on, then the function 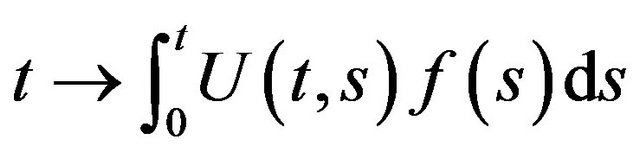is Holder continuous with any exponent.

Condition 4) ensures the generated evolution operator satisfies 4) (see [6], Proposition 2.1).

Proposition 1 (see [11]) The family of operators is continuous in t in the uniform operator topology uniformly for s.

Lemma 1 (see [11]) Consider the initial value problem (1.1) in E. If 1)-4) hold, then, for any, there exists a unique continuous function such that and 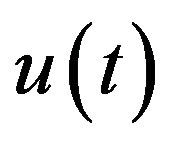satisfies the integral equation

.

is called a mild solution of (1.1).

By Lemma 1, the (mild) solution of (1.1) determines a map from H into itself:. Obviously, is a discrete semidynamic system in H, since is a ω-periodic function with respect to.

3. Main Result

Theorem 1 Assume that (1.2), 1)-4) and

hold, then system (1.1) has a unique continuous ω-periodic solution which attracts any bounded set exponentially. The process associated with (1.1) possesses a global periodic attractor.

Proof. Let be two solutions of problem (1.1) with initial values, and

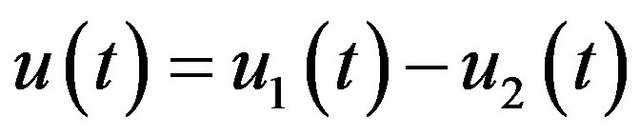. Then by (1.1), we find

(3.1)

Taking the inner scalar product of each side of (3.1) with 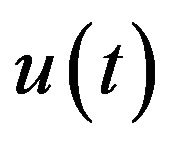in H, and we see that

(3.2)

For the third term on the left of (3.2), by (1.2), we have

(3.3)

From (3.1)-(3.3), we find

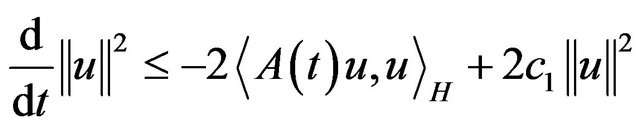
and if

we might as well assume

from the Gronwall’s inequality, we have that

(3.4)

Now considering ω-mapping

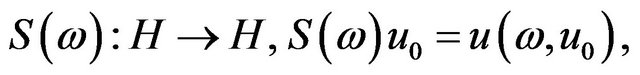
where is the solution of (1.1),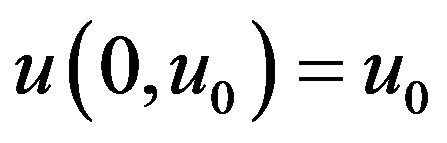. From (3.4), 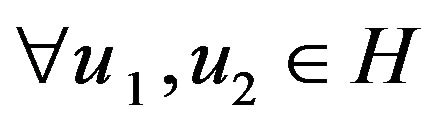, we obtain

.

Thus is a contraction mapping. By Banach’s fixed point theorem, there exists a unique fixed point 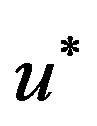for in H such that. At the same time, since is a discrete semidynamic system in H, we can deduce

and

where is the solution passing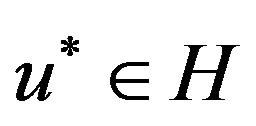. Thus 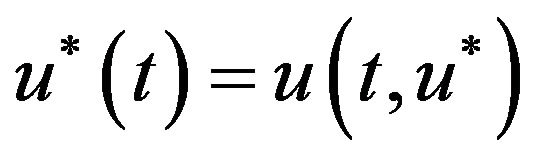is a ω-periodic solution of system (1.1). By (3.4), attracts any bounded set exponentially, which is a global periodic attractor of System (1.1). The proof is completed.

4. Examples

In this section, as an illustration of the main result in Section 3, we consider one example of System (1.1) and get the corresponding results. We consider an evolution equation (i.e., 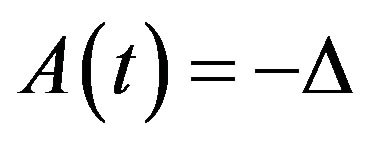in (1.1)) studied in [2,3]:

(4.1)

and if the function f is continuous ω-periodic in t, we have the following theorem.

Theorem 2 System (4.1) possesses a global ω-periodic attractor which attracts any bounded set exponentially, if (where is the first eigenvalue of operator that subjects to the homogeneous Dirichlet boundary condition).

5. Acknowledgements

This work is supported by the National Natural Science Foundation of China under Grant 11101265 and 61075115.

REFERENCES