Advances in Pure Mathematics
Vol.3 No.2(2013), Article ID:28587,5 pages DOI:10.4236/apm.2013.32037
S1-Equivariant CMC Surfaces in the Berger Sphere and the Corresponding Lagrangians
Department of Mathematics, Tokai University, Tokyo, Japan
Email: kikuchi@jewel.ocn.ne.jp
Received October 4, 2012; revised November 30, 2012; accepted December 17, 2012
Keywords: s1-equivariant CMC surfaces; Conservation laws
ABSTRACT
The periodic s1-equivariant hypersurfaces of constant mean curvature can be obtained by using the Lagrangians with suitable potential functions in the Berger spheres. In the corresponding Hamiltonian system, the conservation law is effectively applied to the construction of periodic s1-equivariant surfaces of arbitrary positive constant mean curvature.
1. Introduction
W.-Y. Hsiang [1] investigated the rotation hypersurfaces of constant mean curvature in the hyperbolic or spherical ![]() -space. In [2], Eells and Ratto have constructed the rotation (
-space. In [2], Eells and Ratto have constructed the rotation ( -equivariant) minimal hypersurfaces in the unit 3-sphere with standard metric by using a certain first integral, which is invariant with respect to the rotation angle of generating curves on the orbit space. In [3], a family of
-equivariant) minimal hypersurfaces in the unit 3-sphere with standard metric by using a certain first integral, which is invariant with respect to the rotation angle of generating curves on the orbit space. In [3], a family of  -equivariant periodic CMC surfaces was constructed in the Berger spheres when the constant mean curvature (CMC) is a sufficiently small positive number, and it was cleared that the conserved quantity can be obtained by using the Lagrangian equipped with suitable potential function of the corresponding dynamical system with respect to the Hsiang-Lawson metric [1,4] on the orbit space via the Hamilton equation, where the rotation angle of generating curves can be regarded as “time”. We should remark that the corresponding Lagrangian has the vanishing potential when we construct the
-equivariant periodic CMC surfaces was constructed in the Berger spheres when the constant mean curvature (CMC) is a sufficiently small positive number, and it was cleared that the conserved quantity can be obtained by using the Lagrangian equipped with suitable potential function of the corresponding dynamical system with respect to the Hsiang-Lawson metric [1,4] on the orbit space via the Hamilton equation, where the rotation angle of generating curves can be regarded as “time”. We should remark that the corresponding Lagrangian has the vanishing potential when we construct the  -equivariant minimal hypersurfaces. However, in case that we construct the
-equivariant minimal hypersurfaces. However, in case that we construct the  -equivariant non-minimal CMC-hypersurface in the Berger sphere, the potential of the Lagrangian is a nonvanishing function. In Theorem 4.3, we determine the potential function of the Lagrangian which corresponds to the
-equivariant non-minimal CMC-hypersurface in the Berger sphere, the potential of the Lagrangian is a nonvanishing function. In Theorem 4.3, we determine the potential function of the Lagrangian which corresponds to the  -equivariant CMCsurfaces immersed in the Berger sphere. As a result we can obtain a family of periodic
-equivariant CMCsurfaces immersed in the Berger sphere. As a result we can obtain a family of periodic 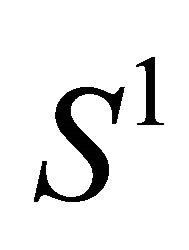 -equivariant CMC surfaces in the Berger spheres when the constant mean curvature is an arbitrary positive number (Theorem 5.2).
-equivariant CMC surfaces in the Berger spheres when the constant mean curvature is an arbitrary positive number (Theorem 5.2).
2. Preliminaries
In [3], a generalized inner product 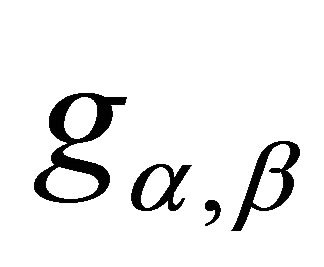 on the unit 3- sphere
on the unit 3- sphere  was defined by
was defined by

where ,
, and
and 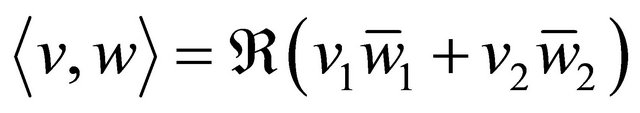 ,
,  and
and  are positive and nonnegative parameters, respectively. The Cartan hypersurface
are positive and nonnegative parameters, respectively. The Cartan hypersurface  in the unit 4-sphere is covered by
in the unit 4-sphere is covered by  (via an 8-fold covering), whose metric is rescaled along the Hopf fibres and its metric on
(via an 8-fold covering), whose metric is rescaled along the Hopf fibres and its metric on  coincides with
coincides with  [5,6]. The family of metrics
[5,6]. The family of metrics  defined on
defined on  contains this one as a special case. In particular
contains this one as a special case. In particular  is a left-invariant metric on
is a left-invariant metric on  and
and 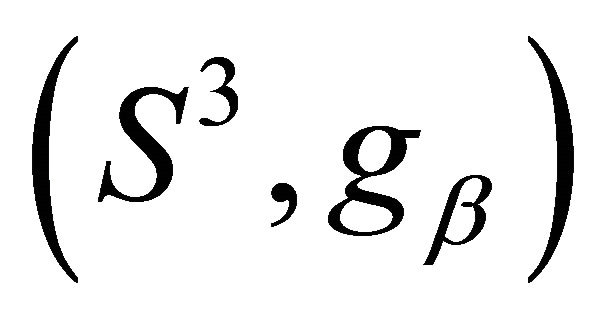 is called the Berger sphere with metric
is called the Berger sphere with metric  in case that
in case that . The Berger metrics
. The Berger metrics  are obtained from the canonical metric by multiplying the metric along the Hopf fiber by
are obtained from the canonical metric by multiplying the metric along the Hopf fiber by 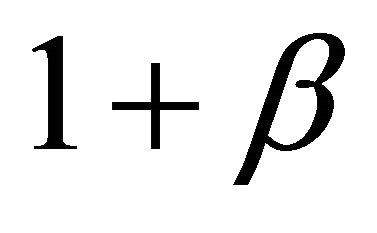 [7].
[7].
Throughout the paper we consider the Berger spheres . Here we summarize the notations which are used in the paper.
. Here we summarize the notations which are used in the paper.
 denotes the orbit space by
denotes the orbit space by  -isometric
-isometric  - ction
- ction  as follows.
as follows.

As the parametrization of  we use the following map:
we use the following map:
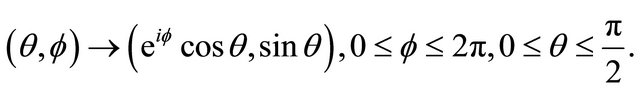
 stands for the orbital metric on
stands for the orbital metric on  :
:

 is the volume function of orbits and
is the volume function of orbits and  is the Hsiang-Lawson metric on
is the Hsiang-Lawson metric on :
:

where

 denotes a curve parametrized by arclength
denotes a curve parametrized by arclength . And also
. And also  and
and  stand for the tension fields of
stand for the tension fields of  with respect to the metrics
with respect to the metrics  and
and , respectively. The geodesic curvature
, respectively. The geodesic curvature 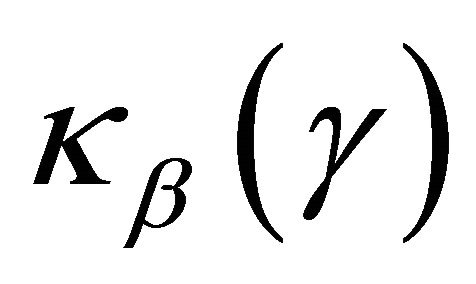 at
at  is defined by
is defined by  where
where  denotes the unit normal vector field to
denotes the unit normal vector field to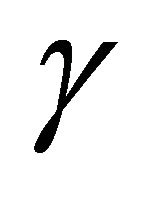 .
.
3. S1-Equivariant CMC-Immersion
For a curve , we consider an
, we consider an  -equivariant map
-equivariant map  such that
such that  , where
, where  and
and  are Riemannian submersions. Throughout the paper, we assume that
are Riemannian submersions. Throughout the paper, we assume that  is an
is an  -equivariant constant mean curvature
-equivariant constant mean curvature  immersion. Then we have
immersion. Then we have
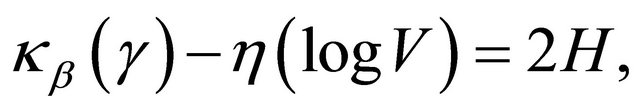 (1)
(1)
since

On the orbit space , the velocity vector field of a curve
, the velocity vector field of a curve  is given by the following component functions.
is given by the following component functions.
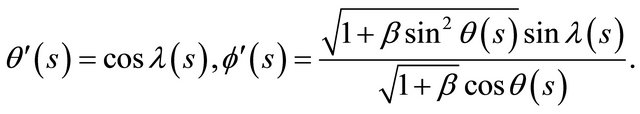
Lemma 3.1. The following formulas hold on  .
.
 (2)
(2)
 (3)
(3)
where
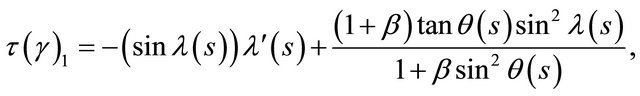
and

Then using the formula (1) we have the following differential Equation (4) of generating curves which corresponds to the CMC-rotation hypersurfaces immersed in , since using Lemma 3.1 the geodesic curvature
, since using Lemma 3.1 the geodesic curvature  is given by
is given by
 (4)
(4)
4. Conservation Laws
We consider a generating curve 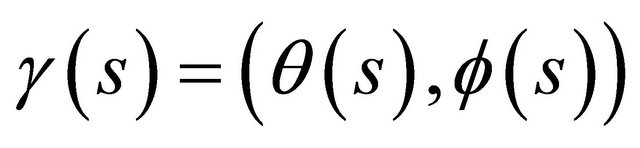 on
on  such that
such that 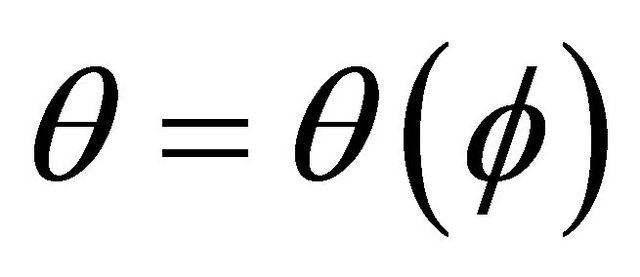 and
and . Then we can consider the space
. Then we can consider the space  of motion with
of motion with 
and time . Let
. Let 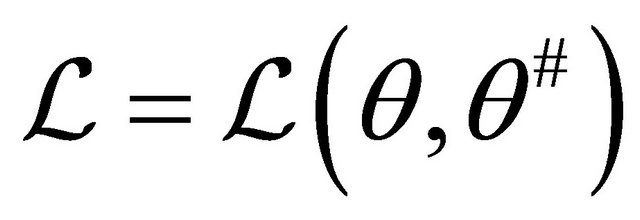 be a Lagrangian on
be a Lagrangian on . Via the Legendre transformation we have the Hamiltonian
. Via the Legendre transformation we have the Hamiltonian  on the phase space
on the phase space :
:

The conservation laws of our system imply the following Proposition 4.1. Let the Lagrangian  on
on  be the following form:
be the following form:
 where
where  is the Hsiang-Lawson metric on
is the Hsiang-Lawson metric on  and
and  is a potential function on the configuration space.
is a potential function on the configuration space.
Then we have
 (5)
(5)
where the conserved quantity in the formula represents the Hamiltonian of our system.
By means of the Hamilton equation (5), we shall determine the potential  which corresponds to the
which corresponds to the  -equivariant CMC surfaces immersed in
-equivariant CMC surfaces immersed in 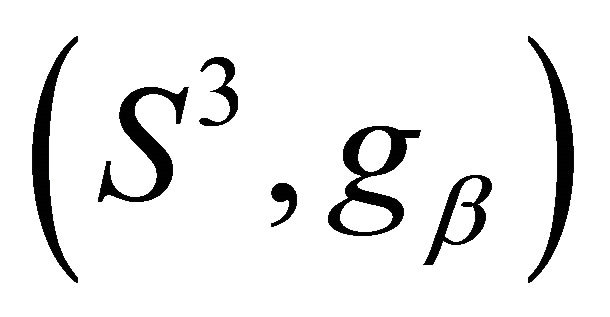 via the differential Equation (4) of generating curves on the orbit space
via the differential Equation (4) of generating curves on the orbit space .
.
The direct computation yields the following Lemma 4.2. Assume that  and
and  are functions of
are functions of
 and
and . Then we have
. Then we have
 (6)
(6)
where

As a consequence, we have the following Theorem 4.3. On our system, the Lagrangian  and the Hamiltonian
and the Hamiltonian  which correspond to the
which correspond to the  -equivariant CMC-H hypersurface immersed in
-equivariant CMC-H hypersurface immersed in  can be determined as follows:
can be determined as follows:

Proof. Using Lemma 4.2 and the differential equation of generating curves (4) we have

from which we obtain
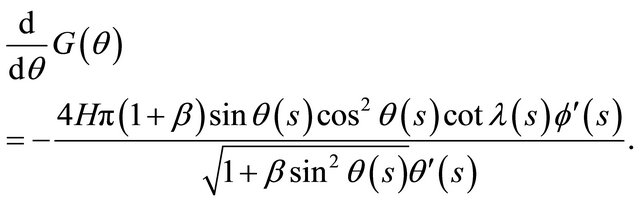
Since  is a constant mean curvature and
is a constant mean curvature and
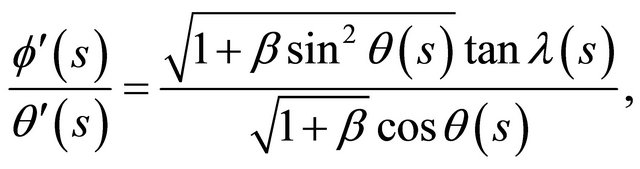
we can choose such as . Q.E.D.
. Q.E.D.
5. Generating Curves for S1-Equivariant CMC Surfaces
Let  be a generating curve on
be a generating curve on  such that
such that  and
and  with the arc length
with the arc length . Then we set the following initial conditions:
. Then we set the following initial conditions:

The Hamilton equation  (Theorem 4.3) implies that
(Theorem 4.3) implies that

from which we have
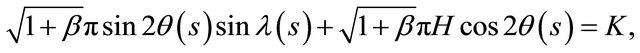
where

On the other hand, using the formulas

and

we have

Consequently we have the following Lemma 5.1. Under the initial conditions for generating curves which correspond to the CMC-H rotation hypersurfaces, we have

and
 (resp.,
(resp., ) if and only if,
) if and only if,

where

Assume that  is an arbitrary positive number. In Lemma 5.1 we now choose
is an arbitrary positive number. In Lemma 5.1 we now choose  such that
such that
 .
.
From Lemma 5.1,  and there exists the value
and there exists the value  of
of  such that
such that  decreases strictly until
decreases strictly until , where the value of
, where the value of  equals to zero at
equals to zero at , and
, and  takes a local minimum at
takes a local minimum at . In fact, if
. In fact, if  does not take a local minimum, then we may assume that there exists
does not take a local minimum, then we may assume that there exists 
such that  and
and
 .
.
Then from the differential equation (4) of generating curves it follows that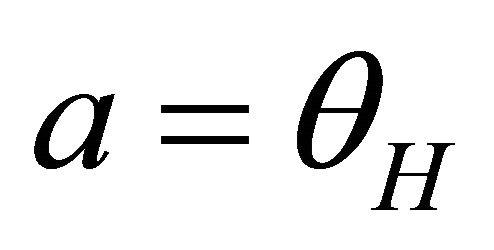 . On the other hand we obtain the following formula:
. On the other hand we obtain the following formula:
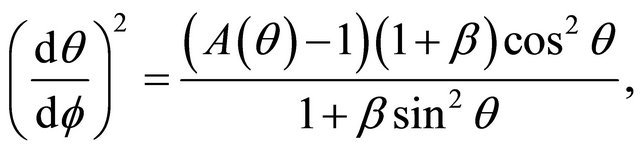 (7)
(7)
where

The formula (7) implies that
 (8)
(8)
where

The formula  implies that
implies that

from which we have

since .
.
Hence we see that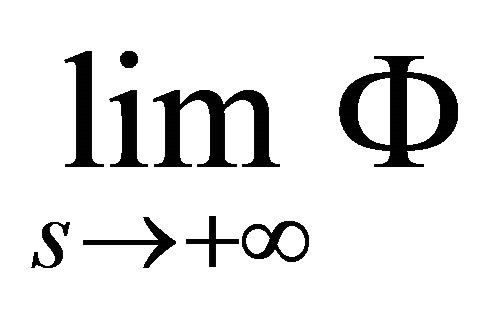 is a positive number. Now if
is a positive number. Now if , then
, then , which implies that
, which implies that  and
and
 , hence
, hence , which is a contradiction. Therefore, the value
, which is a contradiction. Therefore, the value  is not zero.
is not zero.
Consequently, since , from the formula (8)
, from the formula (8)
we see that  is not zero, which contradicts the assumption
is not zero, which contradicts the assumption . Hence
. Hence 
takes a local minimum.
Thus we can continue as the curve satisfying the differential Equation (4) by the reflection. Let
as the curve satisfying the differential Equation (4) by the reflection. Let  be the right hand side of (7). We can define
be the right hand side of (7). We can define  by
by  as follows:
as follows:

Consequently we have the following Theorem 5.2. Let  be an arbitrary positive number and choose
be an arbitrary positive number and choose  such that
such that . If
. If  is a rational number, then the corresponding
is a rational number, then the corresponding  -equivariant hypersurface is an immersed CMC-H torus in the Berger sphere
-equivariant hypersurface is an immersed CMC-H torus in the Berger sphere . In particular, if
. In particular, if  is an integer, then this CMC-H torus is embedded.
is an integer, then this CMC-H torus is embedded.
Theorem 5.3. In the case , Then the corresponding
, Then the corresponding  -equivariant CMC-H hypersurface in the Berger sphere
-equivariant CMC-H hypersurface in the Berger sphere 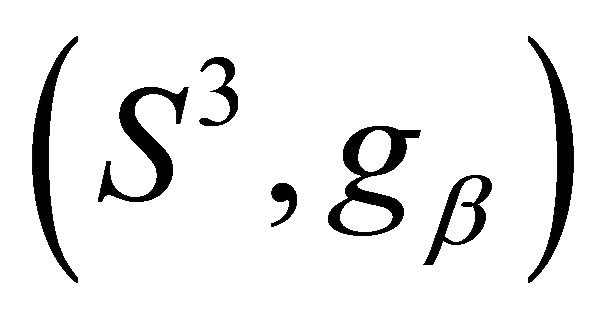 is an extended Clifford torus
is an extended Clifford torus

where

Corollary 5.4. There exists an embedded minimal torus in the Berger sphere 

6. Acknowledgements
I am grateful to Yoshihiro Ohnita and Junichi Inoguchi for their encouragement.
REFERENCES
- W.-Y. Hsiang, “On Generalization of Theorems of A. D. Alexandrov and C. Delaunay on Hypersurfaces of Constant Mean Curvature,” Duke Mathematical Journal, Vol. 49, No. 3, 1982, pp. 485-496. doi:10.1215/S0012-7094-82-04927-4
- J. Eells and A. Ratto, “Harmonic Maps and Minimal Immersions with Symmetries,” Annals of Mathematics Studies, No. 130, 1993.
- K. Kikuchi, “The Construction of Rotation Surfaces of Constant Mean Curvature and the Corresponding Lagrangians,” Tsukuba Journal of Mathematics, Vol. 36, No. 1, 2012, pp. 43-52.
- W.-Y. Hsiang and H. B. Lawson, “Minimal Submanifolds of Low Cohomogeneity,” Journal of Differential Geometry, Vol. 5, 1971, pp. 1-38.
- D. Ferus and U. Pinkall, “Constant Curvature 2-Spheres in the 4-Sphere,” Mathematische Zeitschrift, Vol. 200, No. 2, 1989, pp. 265-271. doi:10.1007/BF01230286
- H. Muto, Y. Ohnita and H. Urakawa, “Homogeneous Minimal Hypersurfaces in the Unit Spheres and the First Eigenvalues of Their Laplacian,” Tohoku Mathematical Journal, Vol. 36, No. 2, 1984, pp. 253-267. doi:10.2748/tmj/1178228851
- P. Petersen, “Riemannian Geometry,” Graduate Texts in Mathematics, 2nd Edition, Vol. 171, Springer-Verlag, New York, 2006.

