World Journal of Condensed Matter Physics
Vol.05 No.02(2015), Article ID:56782,17 pages
10.4236/wjcmp.2015.52012
Tomonaga-Luttinger Unusual Exponents around Fermi Points in the One-Dimensional Hubbard Model
Nelson O. Nenuwe1, John O. A. Idiodi2
1Department of Physics, Federal University of Petroleum Resources, Effurun, Nigeria
2Department of Physics, University of Benin, Benin City, Nigeria
Email: nenuwe.nelson@fupre.edu.ng
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 April 2015; accepted 25 May 2015; published 29 May 2015
ABSTRACT
We study the correlation functions of one-dimensional Hubbard model in the presence of external magnetic field through the conformal field method. The long distance behaviour of the correlation functions and their unusual exponents for the model in the presence of a magnetic field are developed by solving the dressed charge matrix equations and setting the number of occupancies 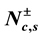 to one, as alternative to the usual zero used by authors in literatures. This work shows that the exponent of the correlation functions is a monotonous function of magnetic field and the correlation functions decay as powers of these unusual exponents. As the magnetic field goes to zero, we obtain the exponents as 8.125, 11.125, 17.125, 26.125 and 38.125 at
to one, as alternative to the usual zero used by authors in literatures. This work shows that the exponent of the correlation functions is a monotonous function of magnetic field and the correlation functions decay as powers of these unusual exponents. As the magnetic field goes to zero, we obtain the exponents as 8.125, 11.125, 17.125, 26.125 and 38.125 at 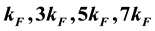 and
and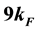 . Our analytical results will provide insights into criticality in condensed matter physics.
. Our analytical results will provide insights into criticality in condensed matter physics.
Keywords:
Correlation Functions, Magnetic Field, Unusual Exponents

1. Introduction
Almost twenty five years ago, Frahm and Korepin introduced the calculation of critical exponents for the one-dimensional (1D) Hubbard model, using the finite size scaling and the principle of conformal field theory (CFT) [1] . This enabled theorists to explore the physics of 1D correlated electron systems. Notwithstanding significant works, the understanding of the behaviour of correlated electron systems is not yet complete. In one dimension, the Hubbard Hamiltonian provides opportunity to study correlation effects in 1D models and the correlation functions decay as power of the distance [2] - [4] . It is the calculation of the critical exponents characterizing this power-law behaviour that have attracted constant theoretical interest. Outstanding results in this field
(with correlation exponents 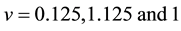 for
for 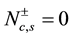 at zero magnetic field around the Fermi points
at zero magnetic field around the Fermi points
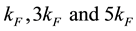 ) have been obtained from conformal field techniques, perturbation calculations and renormalization group methods in different models [1] [5] -[7] . For our calculation, we obtain the correlation exponents as
) have been obtained from conformal field techniques, perturbation calculations and renormalization group methods in different models [1] [5] -[7] . For our calculation, we obtain the correlation exponents as
8.125, 11.125, 17.125, 26.125 and 38.125 around 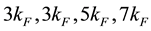 and
and 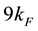 by setting the parameter characterizing particle-hole excitation to one
by setting the parameter characterizing particle-hole excitation to one 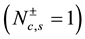 as the magnetic field goes to zero, and the unusual expo-
as the magnetic field goes to zero, and the unusual expo-
nent of the correlation function changes monotonically with change in magnetic field. The progress made in the understanding of critical phenomena in quantum systems as a result of conformal invariance have provided great insights to the problem of calculation of these critical exponents [8] . Although, interacting 1D quantum systems might carry countless low-energy excitations, with linear dispersion relations, but with different Fermi velocities, so the systems are not Lorentz invariant [9] . When the motions of these excitations are decoupled, one can now apply the CFT [10] . Usually, in the application of the conformal field techniques, the nonnegative integer 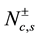 characterizing particle-hole excitations is always taken as zero, but in this paper we shall calculate the electron
characterizing particle-hole excitations is always taken as zero, but in this paper we shall calculate the electron
field correlation function and the density-density correlation function by setting the parameter 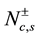 to one, and
to one, and
investigate how this affects the conformal dimensions and critical exponents of the correlation functions. This paper is organized as follows. In Section 2, we review the Bethe Ansatz equations of the Hubbard model and the analytic form of the correlation functions predicted by CFT is given. The dressed charge matrix elements are also calculated with the Wiener-Hopf technique and these elements are used to obtain the magnetic field dependence of the conformal dimensions. The long-distance behaviour of the electron field and density-density correlation functions and their unusual exponents for small magnetic field are calculated in Section 3. The electron field correlation function in momentum space and their Tomonaga-Luttinger (TL) liquid behaviour is examined in Section 4. Finally, Section 5 is devoted to discussion of the properties of the critical exponents for 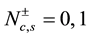 and conclusion.
and conclusion.
2. The Hubbard Model and the Dressed Charge
The Hubbard model is basically the simplest model describing interacting spin-1/2 fermions in many-body physics. In the presence of magnetic field it is defined by the Hamiltonian [11]
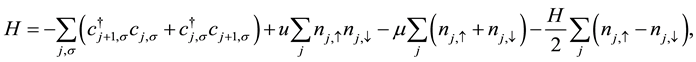 (1)
(1)
where 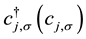 is the creation (annihilation) operator with electron spin σ at site j and
is the creation (annihilation) operator with electron spin σ at site j and 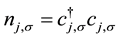 is the
is the
number operator. u is the on-site Coulomb repulsion, μ is the chemical potential and H is the external magnetic field. The hopping integral t = 1. Lieb and Wu [2] has solved Equation (1) exactly and obtained the Bethe Ansatz equations
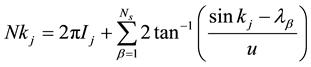 (2)
(2)

where the quantum number Ij and Jα are integers or half-odd integer, 
In the thermodynamic limit, with continuous momentum and rapidity variables, the Lieb-Wu equations become integral equations for the ground state distribution functions of moment a 


The state corresponding to the solution of Equations (2) and (3) has energy and momentum given by


where the conformal dimensions are given by


The positive integers


change in the number of electrons (down-spin) with respect to the ground state, 




and the elements are defined by the solutions of the following coupled integral equations




where the kernel is defined as

The values of 


For small magnetic field we solve the dressed charge matrix equations by Wiener-Hopf technique [12] [13] for terms up to order 

Fourier transforming Equation (17), we obtain

where the kernels are given by

We solve Equation (18) by introducing the function

and expanding it as

where 


The driving terms 





Where the functions 

Also we assume

In terms of these functions we express the Fourier transform of Equation (23) as

where 



where 

Useful special function of 

Using Equations (27) and (28), we obtain

Decompose the right hand side of Equation (32) into the sum of two functions

This implies that

To obtain the solution of Equation (22) for

We decompose the first term by using

The second term of Equation (35) is meromorphic function of 

Note, there is no pole at



Using Equation (39) we can express the function




Applying the formula Equations (41) to (35) and Equation (33), we obtain


Now,

Therefore,


For

The functions 

From Equation (23) for


By definition


where 






As

Simplifying further, we obtain

Using Equation (51), we obtain

Next, the second order contribution to 


From Equation (28)


From Equation (33),

We have decomposed 



where 


From Equation (29), as


Since,

For 




From Equation (34), we obtain

Using

we obtain

Using the value of 

Therefore, with Equations (55) and (69), we obtain

Now to evaluate the dressed charge matrix element 

Applying the same process in the determination of Equation (70), we obtain

Similarly, with the same process, we obtain the other two elements of the dressed charge matrix as

and

From Equation (16) together with the property that 




Using Equation (75) on Equations (70) and (72), we obtain the dressed charge matrix equations as




At half-filling





To obtain the conformal dimensions in terms of small magnetic field we use Equations (80) to (83) on Equations (7) and (8). Note that,

Therefore, the magnetic field dependence of the conformal dimensions are given by


According to the principles of CFT, the general expression for correlation function contains factors from holons and spinons, given by [11]

3. Correlation Functions in Magnetic Field
We now use the results obtained in the last section to obtain the magnetic field dependence of the unusual exponents of the electron field correlation function and density-density correlation function by setting the non-
negative integer
from the quantum numbers (Dc, Ds) = (1/2, −1/2), (3/2, −3/2), (5/2, −5/2), (7/2, −7/2), (9/2, −9/2), ΔNc = 1 and ΔNs = 0. Therefore, the corresponding conformal dimensions for 




where the contributions from 


The critical exponent is given by

This implies that

and

Next, we obtain the conformal dimensions for 




Using Equations (97) and (99) on Equation (87), we obtain

The critical exponent is given by

and

Next, for




Using Equations (104) and (106) on Equation (87), we obtain

The critical exponent is given by

and

For




Using Equations (111) and (113) on Equation (87), we obtain

The critical exponent is given by

and

Finally, for




Using Equations (118) and (120) on Equation (87), we obtain

The critical exponent is given by

and

Combining Equations (92), (100), (107), (114) and (121), we obtain the long-distance asymptotic form of the electron field correlation function with up-spin as

Lastly, we consider the density-density correlation function which originates from the quantum numbers





Again contributions from 

The critical exponents are given by

and

For 


Using Equations (130) and (131) on Equation (87), we obtain

The critical exponents are given by

and

Next, for 


Using Equations (135) and (136) on Equation (87), we obtain


and

Finally, for 


Using Equations (140) and (141) on Equation (87), we obtain


and

4. Correlation Function in Momentum Space
The electron field correlation function Equation (124) has singularities at the Fermi points 



The critical exponent

and

Here we neglect logarithmic field dependence. Equation (145) represents the momentum distribution function around 

Another singularity is at

with critical exponent

Equation (148) exhibits a typical power-law singularity of the TL liquid around the Fermi point

Next at

with the unusual exponent

Also, Equation (150) represents the momentum distribution function around the Fermi point 

At

and

Equation (152) exhibits a typical power-law behaviour of the TL liquid around

Finally, at 

with

and Equation (154) also exhibits typical power-law behaviour of the TL liquid around the Fermi point

5. Discussions
In this paper, we have calculated the electron field and density-density correlation functions and their unusual exponents by using the nonnegative integer 












from the excitation of










In conclusion, the electron field correlation function and the unusual exponents has been obtained around the Fermi points 






References
- Frahm, H. and Korepin, V.E. (1990) Critical Exponents for the One-Dimensional Hubbard Model. Physical Review B, 42, 10553-10565. http://dx.doi.org/10.1103/PhysRevB.42.10553
- Lieb, E.H. and Wu, F.Y. (1968) Absence of Mott Transition in an Exact Solution of the Short-Range, One-Band Model in One Dimension. Physical Review Letters, 20, 1445-1448. http://dx.doi.org/10.1103/PhysRevLett.20.1445
- Woynarovich, F. (1989) Finite-Size Effects in a Non-Half-Filled Hubbard Chain. Journal of Physics A, 22, 4243-4256. http://dx.doi.org/10.1088/0305-4470/22/19/017
- Nenuwe, O.N. and Akpojotor, F. (2015) Power-Law Dependence of Correlation Functions in the Tomonaga-Luttinger Liquid. International Journal of Theoretical and Mathematical Physics, 5, 8-15. http://www.sapub.org/global/showpaperpdf.aspx?doi=10.5923/j.ijtmp.20150501.02
- Parola, A. and Sorella, S. (1990) Asymptotic Spin-Spin Correlations of the
, One-Dimensional Hubbard Model. Physical Review Letters, 64, 1831-1834. >http://html.scirp.org/file/5-4800296x300.png" class="200" />, One-Dimensional Hubbard Model. Physical Review Letters, 64, 1831-1834. http://dx.doi.org/10.1103/PhysRevLett.64.1831
- Finkel’shtein, A.M. (1977) Correlation Functions in One-Dimensional Hubbard Model. JETP Letters, 25, 73-76.
- Luther, A. and Peschel, I. (1975) Calculation of Critical Exponents in Two Dimensions from Quantum Field Theory in one Dimension. Physical Review B, 12, 3906. http://dx.doi.org/10.1103/physrevb.12.3908
- Belavin, A.A. Polyakov, A.M. and Zamolodchikov, A.B. (1984) Infinite Conformal Symmetry in Two-Dimensional Quantum Field Theory. Nuclear Physics B, 241, 333-380. http://dx.doi.org/10.1016/0550-3213(84)90052-X
- Kawakami, N. and Yang, S.-K. (1991) Luttinger Liquid Properties of Highly Correlated Electron Systems in One Dimension. Journal of Physics: Condensed Matter, 3, 5983-6008. http://dx.doi.org/10.1088/0953-8984/3/32/007
- Izergin, A.G., Korepin, V.E. and Reshetikhin, Y. (1989) Conformal Dimensions in Bethe Ansatz Solvable Models. Journal of Physics A, 22, 2615-2620. http://dx.doi.org/10.1088/0305-4470/22/13/052
- Penc, K. and Solyom, J. (1993) One Dimensional Hubbard Model in a Magnetic Field and the Multicomponent Tomonaga-Luttinger Model. Physical Review B, 47, 6273-6292. http://dx.doi.org/10.1103/PhysRevB.47.6273
- Fabian, H.L.E., Frahm, H., Frank, G.O.H., Andreas, K. and Korepin, V.E. (2005) The One-Dimensional Hubbard Model. Cambridge University Press, New York, 1-674.
- Yang, C.N. and Yang, C.P. (1966) One-Dimensional Chain of Anisotropic Spin-Spin Interactions. II. Properties of the Ground-State Energy per Lattice Site for an Infinite System. Physical Review Letters, 150, 327-339. http://dx.doi.org/10.1103/PhysRev.150.327
- Kawakami, N. and Yang, S.-K. (1990) Luttinger Anomaly Exponent of Momentum Distribution in the Hubbard Chain. Physics Letters A, 148, 359-362. http://dx.doi.org/10.1016/0375-9601(90)90818-9
- Qin, S.J. and Yu, L. (1996) Momentum Distribution Critical Exponents for the One-Dimensional Large-U Hubbard Model in the Thermodynamic Limit. Physical Review B, 54, 1447-1450. http://dx.doi.org/10.1103/PhysRevB.54.1447
- Qin, S.J., Liang, S.D., Su, Z.B. and Yu, L. (1995) Density-Matrix Renormalization-Group Calculation of Correlation Functions in the One-Dimensional Hubbard Model. Physical Review B, 52, R5475-R5478. http://dx.doi.org/10.1103/PhysRevB.52.R5475





 , One-Dimensional Hubbard Model. Physical Review Letters, 64, 1831-1834. >http://html.scirp.org/file/5-4800296x300.png" class="200" />, One-Dimensional Hubbard Model. Physical Review Letters, 64, 1831-1834.
, One-Dimensional Hubbard Model. Physical Review Letters, 64, 1831-1834. >http://html.scirp.org/file/5-4800296x300.png" class="200" />, One-Dimensional Hubbard Model. Physical Review Letters, 64, 1831-1834.