International Journal of Intelligence Science
Vol.05 No.01(2015), Article ID:52931,18 pages
10.4236/ijis.2015.51005
Converting Instance Checking to Subsumption: A Rethink for Object Queries over Practical Ontologies
Jia Xu1, Patrick Shironoshita1, Ubbo Visser2, Nigel John1, Mansur Kabuka1
1Department of Electrical and Computer Engineering, University of Miami, Coral Gables, USA
2Department of Computer Science, University of Miami, Coral Gables, USA
Email: j.xu11@umiami.edu, patrick@infotechsoft.com, nigel.john@miami.edu, m.kabuka@miami.edu, visser@cs.miami.edu
Academic Editor: Zhongzhi Shi, Institute of Computing Technology, CAS, China
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 October 2014; revised 25 November 2014; accepted 22 December 2014
ABSTRACT
Efficiently querying Description Logic (DL) ontologies is becoming a vital task in various data-in- tensive DL applications. Considered as a basic service for answering object queries over DL ontologies, instance checking can be realized by using the most specific concept (MSC) method, which converts instance checking into subsumption problems. This method, however, loses its simplicity and efficiency when applied to large and complex ontologies, as it tends to generate very large MSCs that could lead to intractable reasoning. In this paper, we propose a revision to this MSC method for DL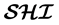 , allowing it to generate much simpler and smaller concepts that are specific enough to answer a given query. With independence between computed MSCs, scalability for query answering can also be achieved by distributing and parallelizing the computations. An empirical evaluation shows the efficacy of our revised MSC method and the significant efficiency achieved when using it for answering object queries.
, allowing it to generate much simpler and smaller concepts that are specific enough to answer a given query. With independence between computed MSCs, scalability for query answering can also be achieved by distributing and parallelizing the computations. An empirical evaluation shows the efficacy of our revised MSC method and the significant efficiency achieved when using it for answering object queries.
Keywords:
Description Logic, Ontology, Object Query,
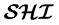 , Most Specific Concept
, Most Specific Concept

1. Introduction
Description logics (DLs) play an ever growing role in providing a formal and semantic-rich way to model and represent structured data in various applications, including semantic web, healthcare and biomedical research, etc. [1] . A knowledge base in description logic, usually referred to as a DL ontology, consists of an assertional component (ABox ) for data description, where individuals (single objects) are introduced and their mutual relationships are described using assertional axioms. Semantic meaning of the ABox data can then be unambi- guously specified by a terminological component (TBox
) for data description, where individuals (single objects) are introduced and their mutual relationships are described using assertional axioms. Semantic meaning of the ABox data can then be unambi- guously specified by a terminological component (TBox ) of the DL ontology, where abstract concepts and roles (binary relations) of the application domain are properly defined.
) of the DL ontology, where abstract concepts and roles (binary relations) of the application domain are properly defined.
In various applications of description logics, one of the core tasks for DL systems is to provide an efficient way to manage and query the assertional knowledge (i.e. ABox data) in a DL ontology, especially for those data-intensive applications; and DL systems are expected to scale well with respect to (w.r.t.) the fast growing ABox data, in settings such as semantic webs or biomedical systems. The most basic reasoning service provided by existing DL systems for retrieving objects from ontology ABoxes is instance checking, which tests whether an individual is a member of a given concept. Instance retrieval (i.e. retrieve all instances of a given concept) then can be realized by performing a set of instance checking calls.
In recent years, considerable efforts have been dedicated to the optimization of algorithms for ontology rea- soning and query answering [2] - [4] . However, due to the enormous amount of ABox data in realistic applications, existing DL systems, such as HermiT [4] [5] , Pellet [6] , Racer [7] and FaCT++ [8] , still have difficulties in handling the large ABoxes, as they are all based on the (hyper) tableau algorithm that is computationally expensive for expressive DLs (e.g. up to EXPTIME for instance checking in DL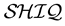 ), where the complexity is usually measured in the size of the TBox, the ABox and the query [9] - [13] . In practice, since the TBox and the query are usually much smaller compared with the ABox, the reasoning efficiency could be mostly affected by the size of the ABox.
), where the complexity is usually measured in the size of the TBox, the ABox and the query [9] - [13] . In practice, since the TBox and the query are usually much smaller compared with the ABox, the reasoning efficiency could be mostly affected by the size of the ABox.
One of the solutions to this reasoning scalability problem is to develop a much more efficient algorithm that can easily handle large amount of ABox data. While another one is to reduce size of the data by either par- titioning the ABox into small and independent fragments that can be easily handled in parallel by existing systems [14] - [16] , or converting the ABox reasoning into a TBox reasoning task (i.e. ontology reasoning with- out an ABox), which could be “somewhat” independent of the data size, the TBox is static and relatively simple, as demonstrated in this paper.
A common intuition about converting instance checking into a TBox reasoning task is the so-called most specific concept (MSC) method [10] [17] [18] that computes the MSC of a given individual and reduces any instance checking of this individual into a subsumption test (i.e. test if one concept is more general than the other). More precisely, for a given individual, its most specific concept should summarize all information of the individual in a given ontology ABox, and should be specific enough to be subsumed by any concept that the individual belongs to. Therefore, once the most specific concept
 of an individual
of an individual
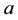 is known, in order to check if
is known, in order to check if
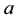 is an instance of any given concept
is an instance of any given concept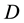 , it is sufficient to test if
, it is sufficient to test if
 is subsumed by
is subsumed by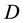 . With the MSC of every individual in the ABox, the efficiency of online object queries can then be boosted by performing an offline classification of all MSCs that can pre-compute many instance checks [10] . Moreover, if a large ontology ABox consists of data with great diversity and isolation, using the MSC method for instance checking could be more efficient than the original ABox reasoning, since the MSC would have the tableau algorithm to explore only the related information of the given individual, potentially restricted to a small subset of the ABox. Also, this method allows the reasoning to be parallelized and distributed, since MSCs are independent of each other and each preserves complete information of the corresponding individual.
. With the MSC of every individual in the ABox, the efficiency of online object queries can then be boosted by performing an offline classification of all MSCs that can pre-compute many instance checks [10] . Moreover, if a large ontology ABox consists of data with great diversity and isolation, using the MSC method for instance checking could be more efficient than the original ABox reasoning, since the MSC would have the tableau algorithm to explore only the related information of the given individual, potentially restricted to a small subset of the ABox. Also, this method allows the reasoning to be parallelized and distributed, since MSCs are independent of each other and each preserves complete information of the corresponding individual.
Despite these appealing properties possessed by the MSC method, the computation of a MSC could be dif- ficult even for a very simple description logic such as . The difficulty arises mainly from the support of qualified existential restrictions (e.g.
. The difficulty arises mainly from the support of qualified existential restrictions (e.g.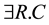 ) in DLs, such that when converting a role assertion (e.g.
) in DLs, such that when converting a role assertion (e.g.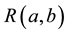 ) of some individuals into an existential restriction, so that information of that given individual may not be preserved completely. For a simple example, consider converting assertions
) of some individuals into an existential restriction, so that information of that given individual may not be preserved completely. For a simple example, consider converting assertions
 and
and
into a concept for individual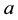 . In this case, we can always find a more specific concept for
. In this case, we can always find a more specific concept for


by increasing


Most importantly, due to the support of existential restrictions, computation of the MSC for a given individual may involve assertions of other entities that are connected to it through role assertions. This implies not only the complexity of the computation for MSCs but also the potential that the resulting MSCs may have larger than desired sizes. In fact, in many of the practical ontology ABoxes (e.g. a social network or semantic webs), most of the individuals could be connected to each other through role assertions, forming a huge connected com- ponent in the ABox graph. Under this situation, the resulting MSC could be extremely large and reasoning with it may completely degenerate into an expensive reasoning procedure.
In this paper, we propose a revised MSC method for DL

The revised MSC method could be very useful for efficient instance checking in many practical ontologies, where the TBox is usually small and manageable while the ABox is in large scale as a database and tends to change frequently. Particularly, this method would be appealing to large ontologies in non-Horn DLs, where current optimization techniques such as rule-based reasoning or pre-computation may fall short. Moreover, the capability to parallelize the computation is another compelling reason to use this technique, in cases where answering object queries may demand thousands or even millions of instance checking tasks.
Our contributions in this paper are summarized as follows:
1) We propose a call-by-need strategy for the original MSC method, instead of computing the most specific concepts offline to handle any given query, which allows us to focus on the current queries and to generate online much smaller concepts that are sufficient to compute the answers. This strategy makes our MSC method suitable for query answering in ontologies, where frequent modifications to the ontology data are not uncommon;
2) We propose optimizations that can be used to further reduce sizes of computed concepts in practical onto- logies for more efficient instance checking;
3) Finally, we evaluate our approach on a range of test ontologies with large ABoxes, including ones gene- rated by existing benchmark tools and realistic ones used in biomedical research. The evaluation shows the efficacy of our proposed approach that can generate significantly smaller concepts than the original MSC. It also

Figure 1. A procedure for instance retrieval for a given query based on our revised MSC method.
shows the great reasoning efficiency that can be achieved when using the revised MSC method for instance checking and query answering.
The rest of the paper is organized as follows: in Section 2, we introduce the background knowledge of a description logic and DL ontology; in Section 3, we give more detailed discussion about the MSC method and our call-by-need strategy; Section 4 presents the technical details of the revised MSC method; Section 5 dis- cusses the related work; Section 6 presents an empirical evaluation on our proposed method; and finally, Section 7 concludes our work.
2. Preliminaries
The technique proposed in this paper is for description logic


2.1. Description Logic

The vocabulary of description logic





Definition 2.1 (


















Definition 2.2 (


where




Description logic



Definition 2.3 (










Definition 2.4 (Simple-Form Concept) A concept is said to be in simple form, if the maximum level of nested quantifiers in this concept is less than 2.
For example, given an atomic concept







Assumption: For accuracy of the technique presented in this paper, without loss of generality, we assume all ontology concepts are in simple form as defined previously, and the concept in any concept assertion is atomic.
2.2. DL Ontologies and Reasoning
Definition 2.5 (




The TBox










The ABox





















An interpretation






If






Definition 2.6 (Logical Entailment) Given an ontology







Definition 2.7 (Instance Checking) Given an ontology



Notice that, instance checking is considered the central reasoning service for information retrieval from ontology ABoxes [19] , and more complex reasoning services, such as instance retrieval, can be realized based on this basic service. Instance checking can also be viewed as a procedure of individual “classification” that verifies if an individual can be classified into some defined DL concepts. An intuition to implement this instance checking service is to convert it into a concept subsumption test by using the so-called most specific concept (MSC) method.
Definition 2.8 (Most Specific Concept [20] ) Let










The MSC method turns the instance checking into a TBox reasoning problem. That is, once the most specific concept





Ontology reasoning algorithm in current systems (e.g. Pellet, and HermiT, etc.) are based on (hyper) tableau algorithms [4] [6] [7] [21] . For details of a standard tableau algorithm for
3. Classification of Individuals
The MSC method for individual checking is based on the idea that, an individual can be classified into a given concept

Using the MSC method for instance checking might eliminate the memory limitation for reasoning with large ABoxes, especially when the ABox




However, as discussed in Section 1, due to the support of existential restrictions in DLs, great complexity for computation of MSC’s may arise when role assertions are involved. Besides, due to the completeness that should be guaranteed by each






3.1. The Call-by-Need Strategy
Since the larger than desired sizes of MSCs are usually caused by its completeness as discussed above, a pos- sible optimization to the MSC method is thus to abandon the completeness that is required to deal with any query concepts, and to apply a “call-by-need” strategy. That is, for an arbitrary query concept




A simple way to realize this strategy is to assign a fresh name















Definition 3.1 Let












Since in our procedure we will add the query concept




3.2. A Syntactic Premise
To decide whether a role assertion could affect classification of a given individual, a sufficient and necessary condition as stated previously is that, the concept behind this assertion conjuncted with other essential information of the individual should be subsumed by the given concept w.r.t.






where





As shown in [16] , for subsumption (1) to hold when





Proposition 3.1 ( [16] ) Let








with


where







This proposition is proven in [16] . It states in fact a syntactic premise in










4. Computation of MSCT
In this section, we present the technique that computes a



4.1. The Rolling-Up Procedure
Converting concept assertions into a concept is straightforward by simply taking conjunction of the involved concepts. When role assertions are involved, the rolling-up technique can be used to transform assertions into a concept by eliminating individuals in them. For example, given the following assertions

transforming them for individual Tom using the rolling up and concept conjunction can generate a single concept assertion

Generalize the Information: The transformation here is for individual Tom, and if individual Mary is not explicitly indicated in the query, it should be sufficient to rewrite





Theorem 4.1 ( [26] ) Let









if and only if

The rolling-up procedure here can be better understood by considering a graph induced by the role assertions to be rolled up, which is defined as follows:
Definition 4.1 A set of ABox role assertions in







Notice that, due to the support of inverse roles in


one node to another. For example, given assertions








The rolling-up for a given individual




for Mary in (3), the rolling-up for Tom should then generate concept

Inverse Role: The support of inverse roles in




Transitive Role: In the rolling-up procedure, no particular care needs to be taken to deal with transitive roles, since any role assertions derived from transitive roles will be automatically preserved [26] . For example, given








Assertion Cycles: This rolling-up technique, however, may suffer information loss if the graph


individuals









It can be found out through ABox reasoning that individual




Multiple solutions to this problem have been proposed, such as an approximation developed by [27] , and the use of cyclic concept definition with greatest fixpoint semantics [24] [28] . In this paper, we choose to use the nominal (e.g.







Based on the discussion so far, the transformation of assertions for a given individual now can be formalized as follows. Let







Notice that, concept
















4.2. Branch Pruning
To apply the call-by-need strategy, the previously defined syntactic premise









This branch pruning technique could be a simple yet an efficient way to reduce complexity of a



where





where





Going beyond such simple ontologies, this optimization technique may also work in complex ontologies, where most of the role assertions in ABox could have


with all roles except






where





Furthermore, with branch pruning, cycles should only be considered in the truncated graph, which may fur- ther simplify the computation of
4.3. Further Optimization and Implementation
The branch pruning here is based on



When computing




makes no contribution to







With these observations, a more rigorous premise based on





with




Case 1 If there is any concept



Case 2 If there is any concept







If either one of the above cases happens, that particular




This optimization is useful to prevent rolling-up of role assertions in an arbitrary direction on existence of related axioms in













With all the insights discussed so far, an algorithm for computation of

Proposition 4.1 (Algorithm Correctness) The algorithm presented in Figure 2 computes a





Proof. We prove by induction.
Basis: For a leaf node





Inductive Step: Let















This algorithm visit every relevant ABox assertion at most once, and it terminates after all related assertions are visited.
5. Related Work
The idea of most specific concept for instance checking was first discussed in [18] , and later extensively studied by [17] [20] for the algorithms and the computational complexity. To deal with existential restrictions when computing the most specific concept, [24] [28] [29] discussed the use of cyclic concepts with greatest fixpoint semantics for preservation of information induced by the role assertions, and [27] also proposed an approxi- mation for most specific concept in DLs with existential restrictions.
On the other hand, for efficient ABox reasoning and instance checking, various optimization techniques have been developed, including lazy unfolding, absorption, heuristic guided search, exploration of Horn clauses of DLs [4] [5] [22] , model merging [2] and extended pseudo model merging technique [3] [30] .
A common direction of these optimization techniques is to reduce the high degree of nondeterminism that is mainly introduced by GCIs in the TBox: given an GCI



Figure 2. A recursive procedure for computation of






Another way to reduce nondeterminism is the exploration of Horn clauses in DLs, since there exist reasoning techniques for Horn clauses that can be deterministic [5] [34] . [5] takes advantage of this in their HermiT reasoner by preprocessing a DL ontology into DL-clauses and invoking the hyperresolution for the Horn clauses, avoiding unnecessary nondeterministic handling of Horn problems in existing DL tableau calculi.
For non-Horn DL, techniques such as model merging [2] and pseudo model merging [30] can be used to capture some deterministic information of named individuals. These techniques are based on the assumption of a consistent ABox and the observation that usually individuals are members of a small number of concepts. The (pseudo) model merging technique merges clash-free tableau models that are constructed by disjunction rules for a consistent ABox, and can figure out individuals that are obviously non-instance of a given concept. For example, if in one tableau model individual







Another option for scalable ABox reasoning is the use of tractable DL languages. For example, the descrip- tion logic


Based on the above lightweight DLs, efficient DL reasoners are developed, such as OWLIM [39] , ELK reasoner [40] , and Oracle’s native inference engine for RDF data sets [41] .
[42] proposed an approximation technique for instance retrieval, which computes both lower bound and upper bound of an answer set of individuals for a given query concept. Their approach invokes an axiom rewriting procedure that converts an ontology in Horn DL into a datalog program, and then uses Oracle's native inference engine to derive the bounds for query answering.
Recently, techniques for partitioning or modularizing ABoxes into logically-independent fragments have been developed [15] [16] . These techniques partition ABoxes into logically-independent modules, such that each will preserve complete information of a given set of individuals, and thus can be reasoned independently w.r.t. the TBox and be able to take advantage of existing parallel-processing techniques.
6. Empirical Evaluation
We implemented the rolling-up procedures for computation of
1) LUBM(s) (LM) are benchmark ontologies generated using the tool provided by [43] ;
2) Arabidopsis thaliana (AT) and Caenorhabditis elegans (CE) are two biomedical ontologies5, sharing a common TBox called Biopax that models biological pathways;
3) DBpedia


Details of these ontologies can be found in Table 1, in terms of DL expressivity, number of atomic concepts (# Cpts), TBox axioms (# Axms), named individuals (# Ind.), and ABox assertions (# Ast.). Notice that, DL
Table 1. Information of tested ontologies.
expressivity of AT and CE is originally

6.1. Complexity of

Using the MSC (or


As we already know, one of the major source of complexity in ontology reasoning is the so-called “and- branching”, which introduces new individuals in the tableau expansion through the




has quantification depth 2 and number of conjuncts 2 (i.e.


6.1.1. Experiment Setup
To evaluate and show efficacy of the proposed strategy and optimization, we have implemented the following three versions of the rolling-up method for comparison:
V1 The original rolling-up procedure adapted to ABox assertions without applying the call-by-need strategy, which computes the most specific concept w.r.t.

V2 The rolling-up procedure with the proposed call-by-need strategy based on
V3 The rolling-up procedure with the call-by-need strategy based on

We compute the


6.1.2. Result Analysis
As we can see from Table 2 and Table 3, the sizes of



Figure 3. Average time (ms) on computation of a
Table 2. Quantification depth of
Table 3. Number of conjuncts of
this paper, which revive the MSC (i.e.

The comparison between V2 and V3 demonstrates the efficacy of the optimization technique discussed in Section 4.3, which could prevent the rolling-up in arbitrary directions by providing a more rigorous precondition based on
In particular, in our previous study of modularization for ontology ABoxes [16] , the biomedical ontologies (i.e. AT and CE ) are found to be complex with many of their ontology roles (33 out of 55) used for concept definitions, and their ABoxes are hard to be modularized even with various optimization techniques applied [16] . However, in this paper, we found much simpler


6.2. Reasoning with

In this section, we will show the efficiency that can be achieved when using the computed


6.2.1. Experiment Setup
We will not compare our method with a particular optimization technique for ABox reasoning, such as lazy unfolding, absorption, or model merging, etc., since they have already been built into existing reasoners and it is usually hard to control reasoners to switch on or off a particular optimization technique. Additionally, the




The


Queries: LUBM comes with 14 standard queries. For biomedical and DBpedia

Figure 4. Queries for biomedical and DBpedia* ontologies.
For each test ontology, we run the reasoning for each of the given queries. We report the average reasoning time spent on instance checking (Figure 5) and instance retrieval (Figure 6), respectively. The reasoning time reported here does not include the time spent for resource initialization (i.e. ontology loading and reasoner initialization), since the initialization stage can be done offline for query answering. However, it is obvious that the



Another point worth noting here is that, for answering object queries using either modular reasoning or the


6.2.2. Result Analysis
As can be seen from the above two figures, using the


Figure 5. Average time (ms) on instance checking.

Figure 6. Average time(s) spent on instance retrieval. Timeout is set to be 100,000 s.
orders of magnitude when comparing with a complete reasoning; 2) and by about two orders of magnitude (except in LUBM1 and LUBM2) when comparing with the modular reasoning. For the latter, the improvement in LUBM1 and LUBM2 are not as significant as in others, which is because of the simplicity of these two onto- logies that allows fine granularity of ABox partitions to be achieved [45] .
On the other hand, using the





where







6.3. Scalability Evaluation
Using the



7. Conclusions and Outlook
In this paper, we proposed a revised MSC method for efficient instance checking. This method allows the ontology reasoning to explore only a much smaller subset of ABox data that is relevant to a given instance checking problem, thus being able to achieve great efficiency and to solve the limitation of current memory- based reasoning techniques. It can be particularly useful for answering object queries over those large non-Horn DL ontologies, where existing optimization techniques may fall short and answering object queries may demand thousands or even millions of instance checking tasks. Most importantly, due to the independence between
Our technique currently works for logic



Figure 7. Scalability evaluation.


Acknowledgements
This work is partly supported by grant # R44GM097851 from the National Institute of General Medical Scien- ces, part of the U.S. National Institutes of Health (NIH).
Cite this paper
JiaXu,PatrickShironoshita,UbboVisser,NigelJohn,MansurKabuka, (2015) Converting Instance Checking to Subsumption: A Rethink for Object Queries over Practical Ontologies. International Journal of Intelligence Science,05,44-62. doi: 10.4236/ijis.2015.51005
References
- 1. Horrocks, I. (2008) Ontologies and the Semantic Web. Communications of the ACM, 51, 58-67.
http://dx.doi.org/10.1145/1409360.1409377 - 2. Horrocks, I.R. (1997) Optimising Tableaux Decision Procedures for Description Logics. Ph.D. Dissertation, University of Manchester, Manchester.
- 3. Haarslev, V. and Möller, R. (2008) On the Scalability of Description Logic Instance Retrieval. Journal of Automated Reasoning, 41, 99-142. http://dx.doi.org/10.1007/s10817-008-9104-7
- 4. Motik, B., Shearer, R. and Horrocks, I. (2007) Optimized Reasoning in Description Logics using Hypertableaux. Proceedings of Conference on Automated Deduction (CADE), 4603, 67-83.
- 5. Motik, B., Shearer, R. and Horrocks, I. (2009) Hypertableau Reasoning for Description Logics. Journal of Artificial Intelligence Research, 36, 165-228.
- 6. Sirin, E., Parsia, B., Grau, B.C., Kalyanpur, A. and Katz, Y. (2007) Pellet: A Practical Owl-Dl Reasoned. Journal of Web Semantics, 5, 51-53. http://dx.doi.org/10.1016/j.websem.2007.03.004
- 7. Haarslev, V. and Möller, R. (2001) RACER System Description. Proceedings of the First International Joint Conference on Automated Reasoning, Siena, June 2001, 701-705.
- 8. Horrocks, I. (1998) Using an Expressive Description Logic: Fact or Fiction? Proceedings of Knowledge Representation and Reasoning, 98, 636-645.
- 9. Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M. and Rosati, R. (2007) Tractable Reasoning and Efficient Query Answering in Description Logics: The DL-Lite Family. Journal of Automated Reasoning, 39, 385-429.http://dx.doi.org/10.1007/s10817-007-9078-x
- 10. Donini, F. (2007) The Description Logic Handbook: Theory, Implementation, and Applications. Cambridge University Press, Cambridge.
- 11. Glimm, B., Horrocks, I., Lutz, C. and Sattler, U. (2008) Conjunctive Query Answering for the Description Logic. Journal of Artificial Intelligence Research, 31, 157-204.
- 12. Ortiz, M., Calvanese, D. and Eiter, T. (2008) Data Complexity of Query Answering in Expressive Description Logics via Tableaux. Journal of Automated Reasoning, 41, 61-98.
http://dx.doi.org/10.1007/s10817-008-9102-9 - 13. Tobies, S. (2001) Complexity Results and Practical Algorithms for Logics in Knowledge Representation. Ph.D. Dissertation, RWTH Aachen, Aachen.
- 14. Guo, Y. and Heflin, J. (2006) A Scalable Approach for Partitioning OWL Knowledge Bases. International Workshop on Scalable Semantic Web Knowledge Base Systems (SSWS), Geogia, November 2006, 636-641.
- 15. Wandelt, S. and Möller, R. (2012) Towards ABox Modularization of Semi-Expressive Description Logics. Applied Ontology, 7, 133-167.
- 16. Xu, J., Shironoshita, P., Visser, U., John, N. and Kabuka, M. (2013) Extract ABox Modules for Efficient Ontology Querying. ArXiv e-Prints. arXiv: 1305.4859
- 17. Donini, F., Lenzerini, M., Nardi, D. and Schaerf, A. (1994) Deduction in Concept Languages: From Subsumption to Instance Checking. Journal of Logic and Computation, 4, 423-452.
http://dx.doi.org/10.1093/logcom/4.4.423 - 18. Nebel, B. (1990) Reasoning and Revision in Hybrid Representation Systems. Vol. 422, Springer-Verlag, Germany.
- 19. Schaerf, A. (1994) Reasoning with Individuals in Concept Languages. Data and Knowledge Engineering, 13, 141-176. http://dx.doi.org/10.1016/0169-023X(94)90002-7
- 20. Donini, F. and Era, A. (1992) Most Specific Concepts for Knowledge Bases with Incomplete Information. Proceedings of CIKM, Baltimore, November 1992, 545-551.
- 21. Tsarkov, D. and Horrocks, I. (2006) FaCT++ Description Logic Reasoner: System Description. Proceedings of 3rd International Joint Conference on Automated Reasoning, Seattle, 17-20 August 2006.
- 22. Horrocks, I. and Sattler, U. (2007) A Tableau Decision Procedure for Mathcal SHOIQ. Journal of Automated Reasoning, 39, 249-276. http://dx.doi.org/10.1007/s10817-007-9079-9
- 23. Horrocks, I. and Tessaris, S. (2000) A Conjunctive Query Language for Description Logic Aboxes. Proceedings of AAAI, Austin, August 2000, 399-404.
- 24. Baader, F. and Küsters, R. (1998) Computing the Least Common Subsumer and the Most Specific Concept in the Presence of Cyclic ALN-Concept Descriptions. In: Herzog, O. and Gunter, A., Eds., KI-98: Advances in Artificial Intelligence, Springer, Bremen, 129-140.
- 25. Krötzsch, M., Rudolph, S. and Hitzler, P. (2008) Description Logic Rules. European Conference on AI, 178, 80-84.
- 26. Horrocks, I., Sattler, U. and Tobies, S. (2000) Reasoning with Individuals for the Description Logic SHIQ. Proceedings of Automated Deduction (CADE), Pittsburgh, June 2000, 482-496.
- 27. Küsters, R. and Molitor, R. (2001) Approximating Most Specific Concepts in Description Logics with Existential Restrictions. In: Baader, Franz, Brewka, Gerhard, Eiter and Thomas, Eds., KI 2001: Advances in Artificial Intelligence, Springer, Vienna, 33-47.
- 28. Baader, F. (2003) Least Common Subsumers and Most Specific Concepts in a Description Logic with Existential Restrictions and Terminological Cycles. International Joint Conference on Artificial Intelligence, 3, 319-324.
- 29. Baader, F., Küsters, R. and Molitor, R. (1999) Computing Least Common Subsumers in Description Logics with Existential Restrictions. International Joint Conference on Artificial Intelligence, 99, 96-101.
- 30. Haarslev, V., Möller, R. and Turhan, A.Y. (2001) Exploiting Pseudo Models for TBox and ABox Reasoning in Expressive Description Logics. International Joint Conference, IJCAR 2001, Siena.
- 31. Hudek, A.K. and Weddell, G. (2006) Binary Absorption in Tableaux-Based Reasoning for Description Logics. Proceedings of the International Workshop on Description Logics (DL 2006), 189, 86-96.
- 32. Tsarkov, D. and Horrocks, I. (2004) Efficient Reasoning with Range and Domain Constraints. Proceedings of the 2004 Description Logic Workshop (DL 2004), 104, 41-50.
- 33. Wu, J., Hudek, A.K., Toman, D. and Weddell, G.E. (2012) Assertion Absorption in Object Queries over Knowledge Bases. International Conference on the Principles of Knowledge Representation and Reasoning, Rome, June 2012.
- 34. Grosof, B., Horrocks, I., Volz, R. and Decker, S. (2003) Description Logic Programs: Combining Logic Programs with Description Logic. Proceedings of WWW, Budapest, May 2003, 48-57.
- 35. Baader, F., Brand, S. and Lutz, C. (2005) Pushing the EL Envelope. Proceedings of IJCAI, Edinburgh, August 2005, 364-369.
- 36. Baader, F., Brandt, S. and Lutz, C. (2008) Pushing the EL Envelope Further. Proceedings of the OWLED 2008 DC Workshop on OWL: Experiences and Directions, Karlsruhe, October 2008.
- 37. Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M. and Rosati, R. (2005) DL-Lite: Tractable Description Logics for Ontologies. Proceedings of AAAI, 5, 602-607.
- 38. Calvanese, D., De Giacomo, G., Lembo, D., Lenzerini, M. and Rosati, R. (2006) Data Complexity of Query Answering in Description Logics. Proceedings of Knowledge Representation and Reasoning (KR), 6, 260-270.
- 39. Bishop, B., Kiryakov, A., Ognyanoff, D., Peikov, I., Tashev, Z. and Velkov, R. (2011) OWLIM: A Family of Scalable Semantic Repositories. Journal of Semantic Web, 2, 33-42.
- 40. Kazakov, Y., Krötzsch, M. and Simancík, F. (2011) Concurrent Classification of EL Ontologies. International Semantic Web Conference, Bonn, October 2011, 305-320.
- 41. Wu, Z., Eadon, G., Das, S., Chong, E.I., Kolovski, V., Annamalai, M. and Srinivasan, J. (2008) Implementing an Inference Engine for RDFS/OWL Constructs and User-Defined Rules in Oracle. Proceedings of IEEE 24th International Conference on Data Engineering (ICDE), Cancun, April 2008, 1239-1248.
- 42. Zhou, Y., Cuenca Grau, B., Horrocks, I., Wu, Z. and Banerjee, J. (2013) Making the Most of Your Triple Store: Query Answering in OWL 2 Using an RL Reasoner. Proceedings of the 22nd International Conference on World Wide Web, Rio, May 2013, 1569-1580.
- 43. Guo, Y., Pan, Z. and Heflin, J. (2005) LUBM: A Benchmark for OWL Knowledge Base Systems. Journal of Web Semantics, 3, 158-182. http://dx.doi.org/10.1016/j.websem.2005.06.005
- 44. Auer, S., Bizer, C., Kobilarov, G., Lehmann, J., Cyganiak, R. and Ives, Z. (2007) DBpedia: A Nucleus for a Web of Open Data. Proceedings of ISWC, Busan, November 2007, 722-735.
- 45. Dean, J. and Ghemawat, S. (2008) MapReduce: Simplified Data Processing on Large Clusters. Communications of the ACM, 51, 107-113. http://dx.doi.org/10.1145/1327452.1327492
NOTES

1Note that, to follow the simple-form concept restriction, multiple axioms may be added.

2Note the axiom equivalence

3Note that







