Received 21 January 2015; accepted 22 April 2015; published 28 April 2015

ABSTRACT

We present a unified approach to describing and linking several methods for representing categorical data in a contingency table. These methods include: correspondence analysis, Hellinger distance analysis, the log-ratio alternative, which is appropriate for compositional data, and the non-symmetrical correspondence analysis. We also present two solutions working with cummulative frequencies.

Keywords:

Correspondence Analysis, Hellinger Distance, Log-Ratio Analysis, Generalized Pearson Contingency Coefficient, Correspondence Analysis with Cumulative Frequencies

1. Introduction

In multivariate analysis, it is usual to link several methods in a closed expression, which depends on a set of parameters. Thus, in cluster analysis, some criteria (single linkage, complete linkage, median), can be unified by using parametric coefficients. The biplot analysis on a centered matrix, is based on the singular value de- composition (SVD)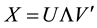. The general solution is 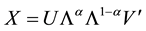with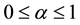, providing the GH, JK, SQ and other biplot types depending on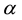. Also, some orthogonal rotations in factor analysis (varimax, quartimax) are particular cases of an expression depending on one or two parameters.

There are several methods for visualizing the rows and columns of a contingency table. These methods can be linked by using parameters and some well-known matrices. This parametric approach shows that correspon- dence analysis (CA), Hellinger distance analysis (HD), non-symmetric correspondence analysis (NSCA) and log-ratio analysis (LR), are particular cases of a general expression. In these methods, the decomposition of the inertia is used as well as a generalized version of Pearson contingency coefficient. With the help of triangular matrices, it is also possible to perform two analyses, Taguchi’s analysis (TA) and double accumulative analysis (DA), both based on cumulative frequencies. This paper unifies and extends some results by Cuadras and Green- acre [1] -[4] .

2. Weighted Metric Scaling

A common problem in data analysis consists in displaying several objects as points in Euclidean space of low dimension.

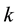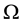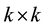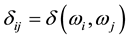Let be a set with objects, a distance function on providing the Eu- clidean distance matrix, where Let 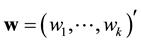a weight vector such that 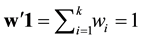with and the column vector of ones.

The weighted metric scaling (WMS) solution using finds the spectral decomposition

, (1)

where is the identity matrix, , is diagonal with positive eigenvalues arranged in descending order, is such that, and [5] .

The matrix contains the principal coordinates of, which can be represented as a configuration of points in Euclidean space. This means that the Euclidean distance between the points, with coordinates the rows, of, equals.

The geometric variability of with respect to is defined by

.

The geometric variability (also called inertia) can be interpreted as a generalized variance [6] .

If and is the column vector with the diagonal entries in, then. Since and, we have. Thus, if, the geometric variability is

.

We should use the first m columns of to represent the objects in low dimension, usually. This provides an optimal representation, in the sense that the geometric variability taking first di- mensions is and this quantity is maximum.

3. Parametric Analysis of Contingency Tables

Let be an contingency table and the correspondence matrix, where. Let and, , , , the vectors and diagonal matrices with the marginal frequencies of. In order to represent the rows and columns of, Goodman [7] intro- duces the generalized non-independence analysis (GNA) by means of the SVD:

,

where is diagonal with the singular values in descending order, and are matrices of appropriate order with, and orthogonal., with, is any monotonically increasing function. Here

with, means. The principal coordinates for rows and columns are given by

,. Clearly GNA reduces to CA when.

A suitable choice of is the Box-Cox transformation

With this transformation, let us consider the following SVD depending on three parameters:

, (2)

where and. Then the principal coordinates for the rows and the standard coordinates for the columns of are given by and, respectively, in the sense that these coordinates reconstitute the model:

.

However, different weights are used for the column representation, e.g.,. Implicit with this (row) representation is the squared distance between rows

. (3)

The first principal coordinates account for a relative high percentage of inertia, see Section 2. This parametric approach satisfies the principle of distributional equivalence and has been explored by Cuadras and Cuadras [2] and Greenacre [4] . Here we use Greenacre’s parametrization.

The geometric variability for displaying rows, is the average of the distances weighted by the row marginal frequencies:

,

where is the matrix of squared parametric distances (3).

For measuring the dispersion in model (2), let us introduce the generalized Pearson contingency coefficient

.

Note that if, i.e., under “statistical independence” between row and column vari- ables. In general.

The unified approach for all methods (centered and uncentered) discussed below, are given in Table 1. It is worth noting that, from

, (4)

the centered and uncentered solutions coincide in CA, NSCA and TA (Taguchi’s analysis, see below).

To give a WMS approach compatible with (1), we mainly consider generalized versions without right-

centering, i.e., post-multiplying by. In fact, we can display columns in the same

graph of rows without applying this post-multiplication. To do this compute the SVD with D diagonal and H_I the unweighted centering matrix. Then and if we take prin- cipal coordinates for the rows, and identify each column as the dummy row profile, then the centered projection provides standard coordinates for the columns, see [2] [3] .

4. Testing Independence

Suppose that the rows and columns of are two sets of categorical variables with and states, and that is the observed frequencies of the corresponding combination, according to a multinomial model. Assuming, the test for independence between row and column variables can be performed with. Under independence we have, as, if, and

if, where is the chi-square distribution with d.f. The con-

vergence is in law.

To prove this asymptotic result, suppose a fix value. Let. From we get

.

But. Hence, under independence, as. Thus

.

If then and the above limit reduces to.

5. Correspondence Analysis

In this and the following sections, we present several methods of representation, distinguishing, when it is necessary, the centered from the uncentered solution. The inertia is given by the geometric variability and the generalized Pearson coefficient, respectively.

Centered and Uncentered

.

1) Chi-square distance between rows:.

2) Rows and columns coordinates:.

3) Inertia:.

Some authors considered CA the most rational method for analyzing contingency tables, because its ability to display in a meaningful way the relationships between the categories of two variable [8] -[10] . For the history of CA, see [11] , and for a continuous extension, see [12] [13] . CA can be understood as the first order approxima- tion to the alternatives HD and LR given below [3] . Besides, LR would be a limiting case of parametric CA [14] .

6. Hellinger Distance Analysis

Centered, Uncentered (

1) Hellinger distance between rows:.

2) Rows and columns coordinates:.

3) Inertia:,

.

Although the distances between rows are the same, the principal coordinates in the centered and uncentered

solutions are distinct. Note that is the so-called affinity coefficient and that.

HD is suitable when we are comparing several multinomial populations and the column profiles should not have influence on the distance. See [15] [16] .

7. Non-Symmetric Correspondence Analysis

Centered and Uncentered

.

1) Distance between rows:.

2) Rows and columns coordinates:.

3) Inertia:.

Note that is related to the Goodman-Kruskal coefficient in a contingency table. This measure is

.

The numerator of represents the overall predictability of the columns given the rows. Thus NSCA may be useful when a categorical variable plays the role of response depending on a predictor variable, see [17] -[19] .

8. Log-Ratio Analysis

Centered, Uncentered

1) Log-ratio distance between rows:.

2) Rows and columns coordinates:,.

3) Inertia:,

.

In spite of having the same distances, the principal coordinates (centered and uncentered) are different. Note that. This method satisfies the principle of subcompositional coherence and is appropriate for positive compositional data [20] .

The inertia and the geometric variability in these four methods, as well as Taguchi’s method given in Section 2, are summarized in Table 2. For a comparison between CA, HD, and LR see [3] [21] . Besides, by varying the parameters there is the possibility of a dynamic presentation linking these methods [22] .

9. Double-Centered Log-Ratio Analysis

In LR analysis Lewi [23] and Greenacre [4] considered the weighted double-centered solution

,

called “spectral map”. The unweighted double-centered solution, called “variation diagram”, was considered by Aitchison and Greenacre [20] . They show that log-ratio and centered log-ratio biplots are equivalent. In this solution the role of rows and columns is symmetric.

10. Analysis Based on Cumulative Frequencies

Let be the contingency table, and the row and column marginals. Given a row let us consider the cumulative frequencies

,

and cumulative column proportions

.

The Taguchi’s statistic [24] , is given by

,

where are weights. Two choices are possible: and. The test based

on is better than Pearson chi-square when there is an order in the categories of the rows or columns of the contingency table [25] .

The so-called Taguchi’s inertia is

By using and the triangular matrix

,

then and. Thus depends on and can be expressed as

.

As it occurs in CA, where the inertia is the trace with, Beh et al. [26] considered the decomposition of Taguchi’s inertia. In our matrix notation. using the above, we have

.

From (4), centering is not necessary here This SVD provides an alternative for visualizing the rows and columns of. The main aspects of this solution, where is the cumulative sum for row and, are:

1) Distance between rows:.

2) Rows and columns coordinates:,.

3) Inertia:

,

where.

There is a formal analogy between and the Goodman-Kruskal coefficient. Also note that the last column in and are equal, so in the index can run from 1 to.

11. Double Acumulative Frequencies

More generally, the analysis of a contingency table may also be approached by using cumulative fre- quencies for rows and columns. Thus an approach based on double accumulative (DA) frequencies is

,

where is a suitable triangular matrix with ones. Clearly matrices, , contain the cumulative frequencies [1] . However, both cumulative approaches TA and DA may not provide a clear display of the contingency table.

Finally, from

,

all (uncentered) methods CA, HD, NSCA, LR, TA and DA can be unified by means of the SVD

,

as it is reported in Table 3. If, we suppose in the null entries of and.

12. An Example

The data in Table 4 is well known. This table combines the hair and eye colour of 5383 individuals. We present the first two principal coordinates (centered solution) of the five hair colour categories for CA, HD, LR and NSCA. We multiply the NSCA solution (denoted by) by 2 for comparison purposes.

These four solutions are similar.

Finally, we show the first two coordinates for Taguchi’s and double accumulative solutions, but multiplying by 3 for comparison purposes.

.

Both solutions are quite distinct from the previous ones.

References