American Journal of Operations Research
Vol.04 No.05(2014), Article ID:49975,11 pages
10.4236/ajor.2014.45031
On a Control Problem Containing Support Functions
I. Husain1, A. Ahmed2, Abdul Raoof Shah2
1Department of Mathematics, Jaypee University of Engineering and Technology, Guna, India
2Department of Statistics, University of Kashmir, Srinagar, India
Email: ihusain11@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 June 2014; revised 15 July 2014; accepted 10 August 2014
ABSTRACT
A control problem containing support functions in the integrand of the objective of the functional as well as in the inequality constraint function is considered. For this problem, Fritz John and Karush-Kuhn-Tucker type necessary optimality conditions are derived. Using Karush-Kuhn-Tucker type optimality conditions, Wolfe type dual is formulated and usual duality theorems are established under generalized convexity conditions. Special cases are generated. It is also shown that our duality results have linkage with those of nonlinear programming problems involving support functions.
Keywords:
Control Problem, Support Function, Optimality Conditions, Generalized Convexity, Wolfe Type Duality, Nonlinear Programming Problem

1. Introduction
Optimal control theory, which is an extension of calculus of variations is a mathematical optimization method for deriving control policies. In essence, an optimal control is set of differential equations describing the path of the control variables that minimize the cost functional. Mond and Hanson [1] were the first to formulate a control problem as a mathematical programming problem and studied Wolfe type duality for the same under convexity of the function involved in the formulation. Subsequently a number of duality results for a control problem involving differentiable functions were obtained, for example, in the references [2] -[5] . There exist applications of optimal control with nondifferentiable terms which appear in the problem of friction. This motivated Chandra et al. [2] to study optimality and duality for a class of nondifferentiable control problem containing the square root of certain quadratic form in the integrand of the objective functional. The popularity of this type of mathematical programming problem seems to originate from the fact that even though the objective functions and/or constraint functions are nonsmooth, a simple representation for the dual may be found. Non smooth mathematical programming theory deals with much more general functions by means of generalized subdifferential [6] and quasidifferential [7] . However, the square root of a positive semidefinite quadratic form and support function are of the few cases of a nondifferentiable function for which subdifferentials can explicitly be written.
In this research we introduce a control problem with a support function in the integrand of the objective functional and each inequality constraint function. Optimality conditions for this nondifferentiable control problem are derived and Wolfe type duality is investigated under pseudoconvexity. Special cases are generated. The linkage between our results and those of nonlinear programming problem containing support function is also indicated.
2. Control Problem and Preliminaries
We introduce the following control problem involving support functions:
(CP): Minimize:
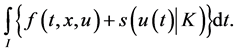
Subject to
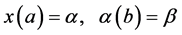 (1)
(1)
 (2)
(2)
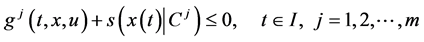 (3)
(3)
where
1)
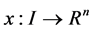 is a differentiable state vector function with its derivative
is a differentiable state vector function with its derivative
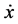 and
and
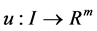 is a smooth control vector function.
is a smooth control vector function.
2)
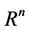 denotes an
denotes an
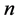 -dimensional Euclidean space and
-dimensional Euclidean space and
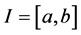 is a real interval, and
is a real interval, and
3)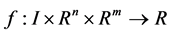 ,
,
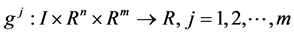 and
and
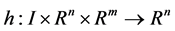 are continuously differentiable.
are continuously differentiable.
4)
 and
and
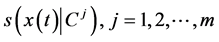 are the support function of the compact set
are the support function of the compact set
 and
and

Denote the partial derivatives of




where superscript denote the vector components. Further

state functions









be written as









of


A support function, being convex and everywhere finite, has a subdifferential in the sense of convex analysis, that is, there exists


As in [8] the subdifferential of








3. Optimality Conditions
In this section, we derive necessary optimality conditions of both Fritz John and Karush-Kuhn-Tucker type for the control problem (CP) stated in the preceding section.
Theorem 1. (Fritz John Conditions): If













Proof: The problem (CP) may be expressed in its abstract version as
(ECD):
subject to
where





By the result of [9] it follows that there exist Langrange multipliers








The condition (12) reduces to


Since












Similar results for







Define the convex function


Now

with


Let




Denoted by



The above is possible by using the representation of





From [10] , it implies that


Now

Consider,

Using (18), (25), (26), we have

Since the integral values for any

The cited lemma assumes that the expression in the square bracket of (27) is piecewise continuous, but this readily extends to measurable. This validates (4). On the basis of analysis needed to validate (28), we can easily establish
Also


By the application of the above-cited lemma, this gives (6) i.e.
The remaining proof of the theorem easily follow on the lines of the proof of Theorem 4.1 of [2] .
Hence the above analysis established the theorem fully.
Chandra et al. [2] pointed out if the optimal solution for (CP) is normal, then the Fritz John type optimal conditions reduce to the following Karush-Kuhn-Tucker optimal conditions:
Theorem 2: If








Such that







4. Wolfe Type Duality
We propose the following dual as the Wolfe type dual and validate duality results amongst (CP) and (WCD).
(WCD): Maximize
subject to





Theorem 3 (Weak Duality): Assume that
1)

2)

3) for all feasible,
is pseudo convex in



Then
Proof: Combining (37) and (38), we have
By the pseudoconvexity hypothesis 3), this yields

Since


implying

and

implying
Since

From (41), we have
This implies
That is,
Theorem 4 (Strong duality): If









Proof: Since









Theorem 5: (Strict Converse Duality): Assume
(H1):

(H2):

(H3):

then

Proof: Assume that









From the feasibility of

This by strict pseudoconvexity hypothesis (H3) yields,
Since

This is absurd. Hence

5. Converse Duality
The problem (WCD) can be written as the follows:
Maximize:
Subject to
where
Consider


pings














and
have weak

Theorem 6. (Converse Duality): Assume
(A1):


(A2):

(A3):



(A4): The matrix

Then

Proof: Since


and piecewise smooth functions











Using (36) and (37) in (42) and (43) respectively, we obtain
The equations can be combined in the matrix form as,
This, due to the hypothesis (A4) yields

Let



The relations (44) together with (48) and (45) respectively imply


From (52) and


From (53) along with


In view of (51) and definition of a normal cone (50) and (51), we have




and

From (52) together with (56) and



imply

From (53) and (57), the feasibility of

Consider
(by using (54), (55) and (56).
This implies that the values of objective functionals of the problem are equal. Consequently in view of the hypothesis of Theorem 1 it implies that

6. Special Cases
Let for




where
and
where
The control problems of the preceding section becomes as the following:
(WCD0): Maximize
Subject to
If



7. Related Nonlinear Programming Problems
If the functions appearing (CP) and (WCD) are independent, of

(CP0): Minimize
subject to
(WCD0): Maximize
subject to
If




(NP1): Minimize
Subject to
(WNP1): Maximize
Subject to
8. Conclusion
Fritz John and Karush-Kuhn-Tucker type necessary optimality conditions for class of nondifferentiable control problems are derived. As an application of Karush-Kuhn-Tucker type necessary optimality conditions, Wolfe type dual is formulated and various duality theorems under generalized convexity conditions are proved. The linkage between our duality results and those of a nonlinear programming problem with support functions is indicated.
References
- Mond, B. and Hanson, M.A. (1968) Duality for Control Problems. SIAM Journal on Control and Optimization, 6, 114-120.
- Chandra, S., Craven, B.D. and Husain, I. (1988) A Class of Nondifferentiable Control Problem. Journal of Optimization Theory and Applications, 56, 227-243. http://dx.doi.org/10.1007/BF00939409
- Hanson, M.A. (1968) Bounds for Functionally Convex Optimal Control Problems. Journal of Mathematical Analysis and Applications, 8, 84-89. http://dx.doi.org/10.1016/0022-247X(64)90086-1
- Pearson, J.D. (1965) Reciprocality and Duality in Control Problems. Journal of Mathematical Analysis and Applications, 10, 383-408. http://dx.doi.org/10.1016/0022-247X(65)90134-4
- Ringlee, R.J. (1965) Bounds for Convex Variational Programming Problems Arising in Power System, Scheduling and Control. IEEE Transaction on Automatic Control, 10, 28-35. http://dx.doi.org/10.1109/TAC.1965.1098077
- Clarke, F.H. (1983) Optimization and Nonsmooth Analysis. Wiley, New York.
- Demyanov, V.F. and Dixon, L.C.W. (1986) Quasidifferential Calculus. North-Holland, Amsterdam. http://dx.doi.org/10.1007/BFb0121132
- Mond, B. and Schechter, M. (1996) Nondifferentiable Symmetric Duality. Bulletin of the Australian Mathematical Society, 53, 177-188. http://dx.doi.org/10.1017/S0004972700016890
- Craven, B.D. and Mond, B. (1979) Langrangean Conditions for Quasi-Differentiable Optimization. Proceedings of the 9th International Conference on Mathematical Programming, Akademiai Kiado, Budapest and North-Holand, Amstedam.
- Kreindler, F. (1966) Reciprocal Optimal Control Problems. Journal of Mathematical Analysis and Applications, 14, 141-152. http://dx.doi.org/10.1016/0022-247X(66)90067-9
- Husain, I. and Jabeen, Z. (2008) Continuous Programming Containing Support Functions. Journal of Applied Mathematics and Informatics, 26, 75-106.
- Husain, I., Abha and Jabeen, Z. (2002) On Nonlinear Programming with Support Functions. Journal of Applied Mathematics and Computing, 10, 83-99.




































































