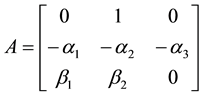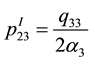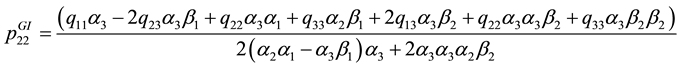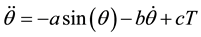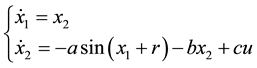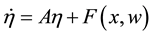Engineering
Vol.07 No.07(2015), Article ID:57932,7 pages
10.4236/eng.2015.77035
On the Comparisons of PID and GI-PD Control
Baishun Liu, Bin He, Xiangqian Luo
Academy of Naval Submarine, Qingdao, China
Email: baishunliu@163.com, BinHe@sina.com, qdqtlxq@sina.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 13 May 2015; accepted 11 July 2015; published 14 July 2015
ABSTRACT
In conjunction with a second order uncertain nonlinear system, this paper makes some comparisons between PID control and general-integral-proportional-derivative (GI-PD) control; that is, by Routh’s stability criterion, we demonstrate that the system matrix under GI-PD control can be stabilized more easily; by linear system theory and Lyapunov method, we demonstrate that GI-PD control can deal with the uncertain nonlinearity more effectively; by analyzing and comparing the integral control action, we demonstrate that GI-PD control has the better control performance. Design example and simulation results verify the justification of our conclusions again. All these mean that GI-PD control has the stronger robustness and higher control performance than PID control. Consequently, GI-PD control has broader application prospects than PID control.
Keywords:
General Integral Control, PID control, GI-PD Control, Robust Control, Output Regulation

1. Introduction
Proportional-integral-derivative (PID) control is certainly the most widely used control strategy today. It is estimated that over 90% of control loops employ PID control [1] . Over the last half-century, a great deal of academic and industrial effort has focused on improving PID control, but the trouble, which often suffers a serious loss of performance due to integrator windup, was not resolved in principle before general integral control [2] appeared in 2009.
After that various general integral controls along with the design techniques were presented. For example, general concave integral control [3] , general convex integral control [4] , constructive general bounded integral control [5] and the generalization of the integrator and integral control action [6] were all developed by resorting to an ordinary control along with a known Lyapunov function; general integral control designs based on linear system theory, sliding mode technique, feedback linearization technique, singular perturbation technique, equal ratio gain technique and power ratio gain technique were presented by [7] - [12] , respectively. Although general integral control has developed rapidly in theory, its practical applications have not been reported. Therefore, in consideration of its good control performance, it is appropriate at this time to compare the simplest general integral control (GI-PD) with PID control in order to promote its applications in practice.
Motivated by the cognition above, in conjunction with a second order uncertain nonlinear system, this paper makes some comparisons between PID control and GI-PD control. The main contributions are: under GI-PD control, it is demonstrated that: 1) the system matrix can be stabilized more easily; 2) it is more effective to deal with the uncertain nonlinear actions; 3) the trouble caused by integrator windup is resolved in principle, and then it has the better control performance; 4) the harmonization of the integral control action and PD control action can be achieved. Moreover, design example and simulation results verify the justification of our conclusions again. All these mean that GI-PD control has the stronger robustness and higher control performance than PID control. Consequently, GI-PD control has broader application prospects than PID control.
Throughout this paper, we use the notation 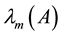 and
and 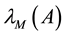 to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive-define bounded matrix
to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive-define bounded matrix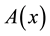 , for any
, for any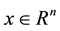 . The norm of vector
. The norm of vector 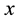 is defined as
is defined as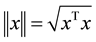 , and that of matrix
, and that of matrix 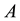 is defined as the corresponding induced norm
is defined as the corresponding induced norm 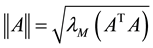 .
.
The remainder of the paper is organized as follows: Section 2 describes the system under consideration, assumption, and stability analysis of the closed-loop system. Section 3 compares Hurwitz stability of the system matrix. Section 4 demonstrates the robustness against the uncertain nonlinearity. Section 5 analyzes the control action. Example and simulation are provided in Section 6. Conclusions are presented in Section 7.
2. Problem Formulation
Consider the following controllable nonlinear system,
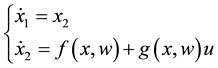 (1)
(1)
where 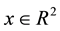 is the state;
is the state; 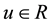 is the control input;
is the control input; 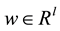 is a vector of unknown constant parameters and disturbances; the function
is a vector of unknown constant parameters and disturbances; the function 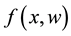 is the uncertain nonlinear actions, the uncertain nonlinear function
is the uncertain nonlinear actions, the uncertain nonlinear function 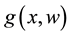 is continuous in
is continuous in 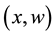 on the control domain
on the control domain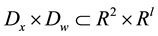 .
.
Assumption 1: There is a unique pair 

so that 


Assumption 2: Suppose that the functions 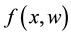
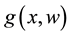


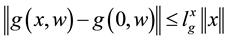

for all 



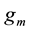

For comparing PID and GI-PD control, the control law is taken as,

where




It is worth to note that although the control law (7) is GI-PD control, it is reduced to PID control as 

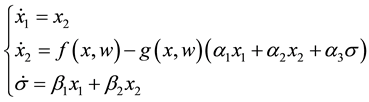
By assumption 1 and choosing 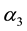

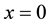
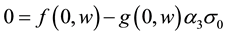
Therefore, we ensure that there is a unique solution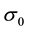

Now, defining
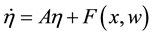
where
and 
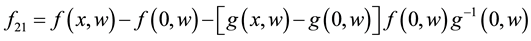
Moreover, it is worthy to note that the function 



By linear system theory, if the matrix 
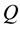



Thus, using 

where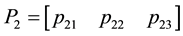
Now, using the inequalities (3), (5), (6) and definition of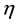
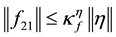
where 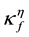
Substituting (13) into (12), obtain,

It is obvious that if

holds, we have
Using the fact that Lyapunov function 


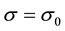
Discussion 1: From the demonstration above, it is obvious that: for ensuring that the closed-loop system is exponentially stable, two key conditions are indispensable, that is, one is that the system matrix 
3. Hurwitz Stability
The polynomials of the system matrix 

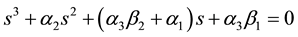
By Routh’s stability criterion and the polynomials (16) and (17), Hurwitz stability conditions of the system matrix 
Under PID control, if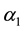
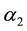

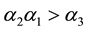
holds, and then the system matrix 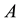
Under GI-PD control, if



holds, then the system matrix 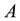
Compared with Hurwitz stability conditions of PID control, the one of GI-PD control has the following features:
1) The striking feature is that the role of gain 



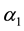
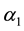
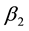




2) As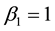


3) The gain 

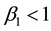
4) There are two additional gains 
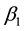

All these means that the system matrix 
4. Robustness against Uncertain Nonlinear Actions
For comparing PID control and GI-PD control robustness against uncertain nonlinear actions, we need to solve the Lyapunov equation 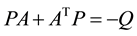
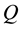

Under PID control, 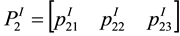
Under GI-PD control, 
For the sake of simplicity, we just consider the case of 

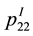

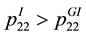
and then by 



where
It is easy to see that there exists 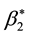

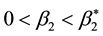
equality (15), we can conclude that GI-PD control is more effective to deal with the uncertain nonlinear actions than PID control. This means that under the case of the same gains
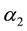




Discussion 2: Although the demonstration above aims at a special case, it is not hard to conclude that by synthesizing all the gains



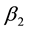
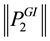
5. Analysis of Control Action
No matter PID control or GI-PD control, Proportional and Derivative control actions are all identical, that is:
Proportional control action is proportional to the error. If the error is small, its corrective effect is small, and vice versa.
Derivative control action is proportional to the rate at which the error is changing. Its corrective effect attempts to anticipate a large error and prevent this future error.
Compared with PID control, the main difference of GI-PD control is the integrator, that is, the error derivative is introduced into the integrator. This lead to an important change of the integral control action, that is,
Under PID control, the integrator is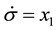
Under GI-PD control, the integrator is




6. Example and Simulation
Consider the pendulum system [13] described by,
where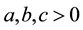
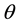


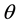

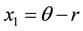

and then it can be verified that 
GI-PD control law is,
It is worth to note that as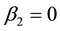
where


and
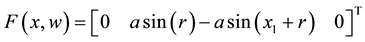
The normal parameters are 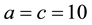
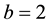


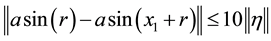
Now, taking
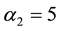



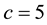
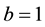

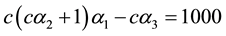
and then the system matrix 




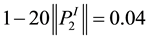
Thus, Under PID and GI-PD control, the asymptotical stability of the whole closed-loop system can all be ensured. Consequently, the simulations are implemented under the normal and perturbed cases, respectively. Moreover, in the perturbed case, we consider an additive impulse-like disturbance 
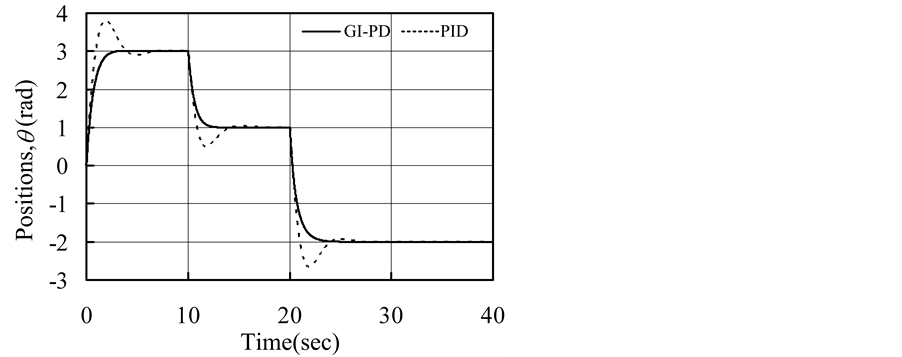
Figure 1 and Figure 2 showed the simulation results under normal and perturbed cases. From the simulation results and design procedure, the following observations can be made: 1) by Hurwitz stability conditions (21) and (22), stability margin of the system matrix 
Figure 1. System output under the normal case.
Figure 2. System output under the perturbed cases.
7. Conclusion
In conjunction with a second order uncertain nonlinear system, this paper makes some comparisons between PID control and GI-PD control. The main contributions are: under GI-PD control, it is demonstrated that: 1) the system matrix can be stabilized more easily; 2) it is more effective to deal with the uncertain nonlinear actions; 3) the trouble caused by integrator windup is resolved in principle, and then it has the better control performance; 4) the harmonization of the integral control action and PD control action can be achieved. Moreover, design example and simulation results verify the justification of our conclusions again. All these means that GI-PD control has the stronger robustness and higher control performance than PID control. Consequently, GI-PD control has broader application prospects than PID control.
Cite this paper
BaishunLiu,BinHe,XiangqianLuo, (2015) On the Comparisons of PID and GI-PD Control. Engineering,07,387-394. doi: 10.4236/eng.2015.77035
References
- 1. Knospe, C.R. (2006) PID Control. IEEE Control Systems Magazine, 26, 30-31.
http://dx.doi.org/10.1109/MCS.2006.1580151 - 2. Liu, B.S. and Tian, B.L. (2009) General Integral Control. Proceedings of the International Conference on Advanced Computer Control, Singapore, 22-24 January 2009, 136-143.
http://dx.doi.org/10.1109/icacc.2009.30 - 3. Liu, B.S., Luo, X.Q. and Li, J.H. (2013) General Concave Integral Control. Intelligent Control and Automation, 4, 356-361.
http://dx.doi.org/10.4236/ica.2013.44042 - 4. Liu, B.S., Luo, X.Q. and Li, J.H. (2014) General Convex Integral Control. International Journal of Automation and Computing, 11, 565-570.
http://dx.doi.org/10.1007/s11633-014-0813-6 - 5. Liu, B.S. (2014) Constructive General Bounded Integral Control. Intelligent Control and Automation, 5, 146-155.
http://dx.doi.org/10.4236/ica.2014.53017 - 6. Liu, B.S. (2014) On the Generalization of Integrator and Integral Control Action. International Journal of Modern Nonlinear Theory and Application, 3, 44-52.
http://dx.doi.org/10.4236/ijmnta.2014.32007 - 7. Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Linear System Theory. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, 5, 3174-3177.
- 8. Liu, B.S. and Tian, B.L. (2012) General Integral Control Design Based on Sliding Mode Technique. Proceedings of the 3rd International Conference on Mechanic Automation and Control Engineering, 5, 3178-3181.
- 9. Liu, B.S., Li, J.H. and Luo, X.Q. (2014) General Integral Control Design via Feedback Linearization. Intelligent Control and Automation, 5, 19-23.
http://dx.doi.org/10.4236/ica.2014.51003 - 10. Liu, B.S., Luo, X.Q. and Li, J.H. (2014) General Integral Control Design via Singular Perturbation Technique. International Journal of Modern Nonlinear Theory and Application, 3, 173-181.
http://dx.doi.org/10.4236/ijmnta.2014.34019 - 11. Liu, B.S. (2015) Equal Ratio Gain Technique and Its Application in Linear General Integral Control. International Journal of Modern Nonlinear Theory and Application, 4, 21-36.
http://dx.doi.org/10.4236/ijmnta.2015.41003 - 12. Liu, B.S. (2015) Power Ratio Gain Technique and General Integral Control. Applied Mathematics, 6, 663-669.
http://dx.doi.org/10.4236/am.2015.64060 - 13. Khalil, H.K. (2007) Nonlinear Systems. 3rd Edition, Electronics Industry Publishing, Beijing, 551, 449-453.