Received 3 January 2016; accepted 12 March 2016; published 15 March 2016

ABSTRACT

We propose a new approach to the investigation of deterministic self-similar networks by using contractive iterated multifunction systems (briefly IMSs). Our paper focuses on the generalized version of two graph models introduced by Barabási, Ravasz and Vicsek ([1] [2] ). We generalize the graph models using stars and cliques: both algorithm construct graph sequences such that the next iteration is always based on n replicas of the current iteration, where n is the size of the initial graph structure, being a star or a clique. We analyze these self-similar graph sequences using IMSs in function of the size of the initial star and clique, respectively. Our research uses the Cantor set for the description of the fixed set of these IMSs, which we interpret as the limit object of the analyzed self-similar networks.

Keywords:

Cantor Set, Fixed Set, Iterated Function Systems, Iterated Multifunction Systems, Self-Similar Graphs

1. Preliminaries and Notations

The aim of this paper is to help connect the results on IMSs ( [3] [4] ) and on self-similar networks ( [1] [2] ). We add a generalization the self-similar models introduced by Barabási, Ravasz and Vicsek and we describe these using IMSs constructed by contractions. We generate self-similar networks from 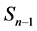stars and 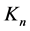cliques, where n is the number of the nodes initially.

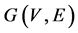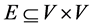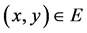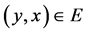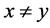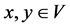Let us consider the pair as a simple graph, where V denotes the finite set of the nodes and such, that for all there exists the edge too, where and. Moreover, the paper doesn’t let the existence of loops and multiegdes, so there exists at least one edge between all pair of different nodes. Let us note with 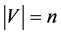the number of the nodes in a given graph.

Let us introduce the 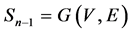notation for a graph with n nodes and 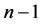edges such that one of the nodes will be connected to all of the others and there will not exist any other edges between the others. Let us refer to this 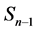as a star with n nodes. On the other hand, let us call the 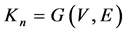graph a clique when all of the possible edges exist in a graph.

The study of graph limits is well known by testing homomorphisms in graphs sequences (see [5] ). The pur- pose is to study the limit self-similar networks using IMSs. We note the iterations of the self-similar networks generated by 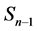stars and 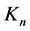cliques the following:

and

respectively.

Based on results known on IMSs (see [3] and [4] ) let us introduce the following notations:

If the functions are singlevalued continuous self operators on a complete metric space X, then is called an iterated function system (IFS). Moreover, the operator given by

is called the fractal operator generated by f. A fixed point of is called a self-similar set of f and if it has a non-integer Hausdorff dimension, then it is called fractal.

Moreover, if are contractions, then is a contraction and its unique fixed point is self-similar. Moreover, if these are similarity contractions (see [6] ), then is a fractal.

Moreover, for any nonempty compact subset, the sequence converges to as.

If the multivalued operators are defined on the X metric space, then we call as an iterated multifunction system (IMS). If the multivalued operators are upper semicontinuous, then the operator given by

is called the fractal operator generated with the IMS F.

An element is a fixed point for T if and only if. Let us note the set of the fixed points with, which we also call as fixed set in the next. In the case of multivalued contractions the same fixed point results hold (see [7] ).

We call a nonempty compact subset self-similar corresponding to the iterated multifunction system F if and only if it is a fixed set for the associated IMS, so.

Let X be the compact set.

We define IFSs on such that their combination using set operations will give us IMSs such that the mappings on correspond to the adjacency matrices of the self-similar networks presented in the following.

We add a simple generalization for two self-similar network models introduced by Barabási, Ravasz and Vicsek ( [1] [2] ). Based on the algorithm introduced in [2] , we create deterministic scale free networks from a star formed by a root and leaves. Moreover, based on [1] we create hierarchical networks con- structed on clique with n nodes.

Firstly, we present the modified version of the algorithm from [1] . We eliminate the step and we generate deterministic scale free networks from a star.

Algorithm 1. Let us note the graph given after the step generated from with. The graph are built by iterations, which reuse the networks generated in the previous steps.

・ Step 0: We init the algorithm from an star formed by a root and leaves.

・ Step 1: We add stars, each unit identical to the network created in the previous step, and we connect each of the new leaves of these units to the initial root (see Figure 1 for).

・ Step 2: We add copies of and connect all bottom nodes of the new units to the initial root (see also Figure 1 for).

These rules can be easily generalized, so the step does the following:

・ Step k: Generally, the creation of adds copies identical to the network created in the previous iteration (step), and we connect each bottom nodes of these units to the initial root of the network.

Secondly, we introduce a simple generalization of the Hierarchical Network Model.

Algorithm 2. We init with a clique with n nodes. Therefore, the steps of the modified algorithm are the following:

・ Step 0: We init the algorithm from an clique, which will be noted as too. We also fix a node from the clique, which will be noted as the initial root in the next.

・ Step 1: We add cliques and we connect nodes from all of the new cliques to a initial root. We refer to the gotten graph as.

・ Step 2: We create with adding replicas of and connecting the new peripheral nodes to the initial root (see Figure 2 for).

These iterations can be also easily generalized, so the step does the following:

・ Step k: We add replicas of itself for creating. We also connect the new peri- pheral nodes to the initial root. This iteration can be continued indefinitely.

After the iteration the graphs generated by a clique or an has nodes.

We have n nodes at the initial step, which are indexed in the following way: the initial root is indexed with 0 and the other nodes are marked with and. The first iteration is followed by indexing the nodes of the replicas: the nodes of the replica will be indexed with, where. We note that in each replica the node will be the node corresponding to the node in the previous iteration. This numbering can be easily generalized to the step: we create replicas of the previous network with nodes. The indexing the nodes of the replicas follows the rule that: the nodes of the replica will be indexed with, where. We also note that

in each replica the node will be the node corresponding to the node in the previous iteration.

Let us look to

as graph sequences. The aim is to characterize these two sequences using IMSs.

Both algorithms constructs the iteration from n replicas of the graph gotten at the iteration, where n is the parameter of the initial star or the initial clique. The application of Algorithm 1 on gives us the self-similar deterministic scale-free network introduced in [1] and the application of Algorithm 2 on construct the self-similar Hierarchial Network Model from [2] , respectively.

Thus, the presented algorithms generate self-similar networks based on stars and cliques.

2. The Graphs’ Adjacency Matrices Generated with Iterated Multifunction Systems

Our paper focuses on two IMSs constructed with set operations of IFSs. We construct these IMSs such that their image will correspond to adjacency matrices projected to.

Let us consider be a simple graph, where. Our construction says that an

undirected edge exists if and only if and.

The aim is to construct IMSs such that their iteration will correspond to same iteration of the self-similar networks’ presented above. This means that in the iteration of an IMS an undirected edge

exists if and only if and, respectively.

3. Construction of the IMSs Corresponding to the Self-Similar Networks

In this section we define those iterated function systems, whose will be used for the characterization of the presented self-similar network. We use these mappings in function of the parameter, which notes the number of nodes of the star and in the clique, respectively. The definitions are followed by the construction of the self-similar networks generated from stars and cliques using these IFSs. Last, we show that the con- struction corresponds to these networks.

Let be functions, where

and let

be the IFS constructed by these functions.

The corresponding iterated function system is defined as follows.

Let be functions, where

and let

be the IFS constructed by these functions.

Let be functions, where

and let

be the IFS constructed by these functions.

We construct the iterated function system corresponding to self-similar networks using the presented and functions.

Theorem 1. The iteration of the iterated multifunction system correspond- ing to can be constructed as the followings:

(1)

where and are the iterated function systems defined above.

Proof. We use mathematical induction for showing that corresponds with the adjacency matrix of. Firstly, we analyze, we look that this corresponds to. It is easy to check that:

(2)

This means that corresponds to the adjacency matrix of star, where the root is indexed with0 and the leaves are indexed with, respectively. (For example, see Figure 3 for.)

Moreover, we show that corresponds to the union created by k replicas of and the

edges between the initial root and the new peripheral nodes.

(3)

Thus, after a reindexig () and a reordering the set operations above we get that the iteration contains n replicas of the IMS corresponding to the iteration.

On the other hand, we use a simple generalization of the Cantor set for showing that and generate the edges which connect the initial root with the peripheral nodes at the step.

It is well known that the iterations of the Cantor set can be easily described using the ternary numeral system:

we note the unit segment with 0 and after the first iteration we note the remaining and

segments with 0 and 2, respectively. The second iteration generates four segments, whose can be marked with and in the ternary numeral system (see Figure 4 for the description). It is easy to check

with induction that the iteration generates all of the segments with length, whose ternary form don’t

contain neither the number 1.

Based on the presented construction of the Cantor set, we describe the set generated by the iteration of

(and by as it’s pair) using the numeral system based on the integer n.

We refer to the sets from (2) with the integers, whose note

an unique value in the context of the numeral system based on the integer n. Based on the definition of, the

second iteration of the IMS is constructed with the union of,

sets. It can be also easily

checked that is the union of the sets with the same i values. Thus, and

from generate the undirected edges between the initial root and the peripheral nodes.

If we transform the values of i from the second iteration to the numeral system based on the integer n, then we get the following forms of the values:

.

We suppose that and from generate the undirected edges (thus, the little boxes in

the adjacency matrix with side length) between the initial root and the new peripheral nodes. Basically,

these peripheral nodes have indexes between and. Moreover, we also suppose that for of the indexes in the numeral system based on the integer n don’t contain neither the number 0.

Last, we show that and from correspond to that undi-

rected edges whose connect the current peripheral nodes with the initial root. Based on the construction using

the numeral system based on the integer n, an iteration of the means that we construct little squares with side length as the followings.

If we have a little box with side length corresponding for an edge between the initial root and the

node in, then generates new edges from it in.

Based on the presumption and the definitions of and the new edges connect the initial root with the peripheral nodes with index, where such, that i is arbitrary and. This

means, that and connect the initial root and the peripheral nodes whose i index is

in such, that it’s form in the numeral system based on the integer n doesn’t contain neither the number 0.

As a conclusion, contains n replicas of and we showed that and add links between the initial root and the replicas’ peripheral nodes just as we described in Algorithm 1. □

Theorem 2. The iteration of the iterated multifunction system corre- sponding to can be constructed as follows:

(4)

where and are the iterated function systems defined above.

Proof. We base the proof on Theorem 1: it is obviously, that the proof of on the IMS differs from proof of the IMS at two notes.

Firstly, we use the IFS as followings: on the k^th iteration of the selected IMS,

will include the same iteration of the IFS, but it won’t include the the set generated by. The

usage of open sets at the set minuses causes that the included sets remain closed as we fixed the condition of existence of the edges.

We also proof the usage of the IFS with mathematical induction: if, then adds little

squares to the adjacency matrix, whose will correspond for the generation of all of the edges and loops in.

On the other hand, using the set minus of exclude the loops. Thus, generates the adjacency

matrix corresponding with a clique with n nodes.

Based on these, we suppose that generates the adjacency matrix corresponding with replicas of a

clique with n nodes. This means, that generates little squares with side length, each

representing a clique with n nodes. By definition, the IMS generates n replicas of the little squares pre-

sented above. Therefore, generates little squares with side length whose correspond

to cliques.

Based on Theorem 1, contains the IMS too, this gives the connection between the initial root and the peripheral nodes at the step (for example, see Figure 5 for and).

This means, that

(5)

Moreover, we also note that if the parameter j of the first set union in (4) goes just to (and not till to k) the IMS generates the same adjacency matrix. It can be easly checked that:

(6)

Thus, the IMS defined on generated the adjacency matrix corresponding with the

step the Algorithm 2 does. □

4. Fixed Sets of the IMSs Corresponding to the Self-Similar Networks

Firstly, it can be easily checked that, and are Banach-type contractions in and there exists a unique fixed point for all of these functions, where.

Secondly, as we showed in Theorem 1, the iteration of and can be easily described using a bit modified version of the Cantor set.

It is well known that the iterations of the classical Cantor set can be described with the ternary numeral

system and we characterized the iterations of and in the numeral system based on

the integer n.

We showed that the step of the Algorithm 1 connects the initial root and the peripheral nodes whose i index is in such that it’s form in the numeral system based on the integer n doesn’t contain neither the number 0.

While the construction of the classical Cantor set adds little segments, which forms in the ternary numeral system don’t contain neither the number 2 our construction adds little squares whose form in the numeral system based on the integer n doesn’t contain neither the number 0. Based on these analogy we refer to and defined on as Cantor type iterated multifunction systems.

So, let us note unique the fixed set of with and the limit of with

, respectively. Moreover, is the the mirror of projected to the first bisector of the plane.

On the other hand, the fixed set of is the whole segment between the and points in. Thus, we note this segment as, referring to the first bisector.

Based on the presented modification of the Cantor set based on the numeral system based on the integer n we can characterize the fixed set of the IMSs and using the and sets presented above.

Theorem 3.

(7)

Proof. We know that and are constructed by Banach-type functions, so there exists a unique fixed set of them. We showed in the proof of Theorem 1 that the IMS constructed by these IFS can be easily described with a modification of the Cantor set. Thus, there exists a fixed set of. Moreover, the can be constructed by infinite union of modified Cantor sets. □

We constructed the IMS using the same and IFSs supplemented by the system.

Theorem 4.

Proof. On, the iteration of the IMS differs from in adding without the iteration of. Based on Equation (5) it is easy to check that the fixed set of is equal with

Thus, the fixed set of corresponds with. □

We characterized the fixed set of IMSs in function of parameter n. We used the Cantor set for describing these fixed sets, which we interpret as limit objects of graph sequences corresponding to self-similar networks.

Acknowledgements

We acknowledge the support of Collegium Talentum. This work was possible due to the financial support of the Sectorial Operational Program for Human Resources Development 2007-2013, co-financed by the European Social Fund, under the project number POSDRU/187/1.5/S/155383 with the title “Quality, excellence, transnational mobility in doctoral research”.

Cite this paper

LeventeSimon,AnnaSoós, (2016) Cantor Type Fixed Sets of Iterated Multifunction Systems Corresponding to Self-Similar Networks. Applied Mathematics,07,365-374. doi: 10.4236/am.2016.74034

References