Applied Mathematics
Vol.06 No.06(2015), Article ID:56854,6 pages
10.4236/am.2015.66085
Study of the Convergence of the Increments of Gaussian Process
Abdelkader Bahram1, Shaban A. El-Shehawy2
1Department of Mathematics, Djillali Liabes University, Sidi Bel Abbès, Algeria
2Department of Mathematics, Faculty of Science, Menoufia University, Shebin El-Kom, Egypt
Email: menaouar_1926@yahoo.fr, shshehawy64@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 April 2015; accepted 30 May 2015; published 2 June 2015
ABSTRACT
Let  be a Gaussian process with stationary increments
be a Gaussian process with stationary increments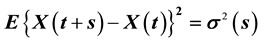 . Let
. Let 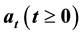 be a nondecreasing function of t with
be a nondecreasing function of t with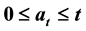 . This paper aims to study the almost sure behaviour of
. This paper aims to study the almost sure behaviour of 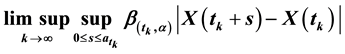 where
where
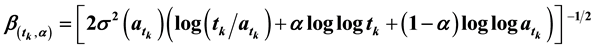
with 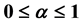 and
and 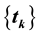 is an increasing sequence diverging to
is an increasing sequence diverging to .
.
Keywords:
Wiener Process, Gaussian Process, Law of the Iterated Logarithm, Regularly Varying Function

1. Introduction
Let 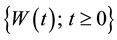 be a standard Wiener process. Suppose that
be a standard Wiener process. Suppose that 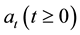 is a nondecreasing function of t such that
is a nondecreasing function of t such that 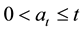 with
with 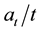 is nonincreasing and
is nonincreasing and  is an increasing sequence diverging to
is an increasing sequence diverging to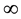 . In [1] the following results are established.
. In [1] the following results are established.
i) If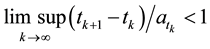 , then
, then

and

where 

ii) If

where


In this paper the limit theorems on increments of a Wiener process due to [1] are developed to the case of a Gaussian process. This can be considered also as an extension of the results to Gaussian processes obtained in [2] . Throughout this paper, we shall always assume the following statements: Let 
surely continuous Gaussian process with










Let 

where 


We define two continuous parameter processes 

and

2. Main Results
In this section we provide the following two theorems which are the main results. We concern here with the development of the limit theorems of a Wiener process to the case of a Gaussian process under consideration the above given assumptions.
Theorem 1. Let 





then

and

where
We note that 
Theorem 2. Let 






then

and

where 

3. Proofs
In order to prove Theorems 1 and 2, we need to give the following lemmas.
Lemma 1. (See [3] ). For any small 



where m is any large number and 
Lemma 2. (See [4] ) Let 






Proof of Theorem 1. Firstly, we prove that

For any 


For instance, let 


The condition (3) is satisfied, and for large k, 



where k is large enough and 


We shall follow the similar proof process as in [5] . Set

Since 


quence 



By (10), for large k we have
where 


Since


Setting
and

we have

Let

and

Then, by (11) and the concavity of 
This implies that
where
Also, the same result for the even subsequence 

To finish the proof of Theorem 1, we need to prove

The proof of (12) is similar to the provided proof in [1] . Thus the proof of Theorem 1 is complete.
Proof of Theorem 2. Firstly, we prove that

According to Lemma 1, we have
provided k is large enough, where 

From the definition of

Thus, (13) is immediate by using Borel Cantelli lemma.
To finish the proof of Theorem 2 we need to prove

Let

Using the well known probability inequality
(see [6] ), one can find positive constants C and K such that, for all
where 



The condition (6) implies that there exists 




where 

4. Some Results for Partial Sums of Stationary Gaussian Sequence
In this section we obtain similar results as Theorems 1 and 2 for the case of partial sums of a stationary Gaussian sequence. Let 








Assume that 







where 

and

respectively, where 

Theorem 3. Under the above statements of



i) If
ii) If
where

Example. Let 


Define random variables


Then
and 




In particular if



5. Conclusion
In this paper, we developed some limit theorems on increments of a Wiener process to the case of a Gaussian process. Moreover, we obtained similar results of these limit theorems for the case of partial sums of a stationary Gaussian sequence. Some obtained results can be considered as extensions of some previous given results to Gaussian processes.
References
- Bahram, A. (2014) Convergence of the Increments of a Wiener Process. Acta Mathematica Universitatis Comenianae, 83, 113-118.
- Hwang, K.S., Choi, Y.K. and Jung, J.S. (1997) On Superior Limits for the Increments of Gaussian Processes. Statistics and Probability Letters, 35, 289-296. http://dx.doi.org/10.1016/S0167-7152(97)00025-4
- Choi, Y.K. (1991) Erdös-Réyi Type Laws Applied to Gaussian Process. Journal of Mathematics of Kyoto University, 31, 191-217.
- Slepian, D. (1962) The One-Sided Barrier Problem for Gaussian Noise. Bell System Technical Journal, 41, 463-501. http://dx.doi.org/10.1002/j.1538-7305.1962.tb02419.x
- Vasudeva, R. and Savitha, S. (1993) On the Increments of Weiner Process―A Look through Subsequences. Stochastic Processes and Their Applications, 47, 153-158. http://dx.doi.org/10.1016/0304-4149(93)90101-9
- Fernique, X. (1975) Evaluations of Processus Gaussian Composes. Probability in Banach Spaces. Lecture Notes in Mathematics, 526, 67-83.

















