International Journal of Modern Nonlinear Theory and Application
Vol.2 No.1(2013), Article ID:28821,9 pages DOI:10.4236/ijmnta.2013.21004
Practical Stabilization for Uncertain Pseudo-Linear and Pseudo-Quadratic MIMO Systems
Università degli Studi di Napoli Federico II, Dipartimento di Informatica e Sistemistica, Napoli, Italy
Email: laura.celentano@unina.it
Received December 4, 2012; revised January 6, 2013; accepted January 14, 2013
Keywords: Practical Stabilization; Linear and Nonlinear Uncertain Systems; Pseudo-Quadratic MIMO Uncertain System; Lyapunov Approach
ABSTRACT
In this paper the problem of practical stabilization for a significant class of MIMO uncertain pseudo-linear and pseudoquadratic systems, with additional bounded nonlinearities and/or bounded disturbances, is considered. By using the concept of majorant system, via Lyapunov approach, new fundamental theorems, from which derive explicit formulas to design state feedback control laws, with a possible imperfect compensation of nonlinearities and disturbances, are stated. These results guarantee a specified convergence velocity of the linearized system of the majorant system and a desired steady-state output for generic uncertainties and/or generic bounded nonlinearities and/or bounded disturbances.
1. Introduction
The problem of practical stability and stabilization for linear and nonlinear systems subject to disturbances and parametric uncertainties together with an efficient robust control has been in the past [1-10] one of the most research topic and nowadays remains actual and significant [11-21].
Indeed there exist many controlled or not systems linear but with uncertain parameters, uncertain pseudo-linear and with bounded coefficients, uncertain pseudoquadratic and with bounded coefficients, having a bounded additional term, for which not always there exists an equilibrium state.
Regarding this, consider:
• the mechanical systems with not viscous friction and/ or with revolute joints (e.g. robots)• the electrical and/or electro-mechanical systems with ferromagnetic devices• many chemical, ecological, meteorological, biological and medical systemswith possible disturbances and reference signals which are non standard (not polynomial or cisoidal).
For the above significant systems, it is important to design a control law such that, in a finite time interval, the state evolution, for all the initial conditions belonging to a specified compact set, is bounded and such that the evolution of the output (also the error signal) converges, with assigned minimum velocity, to chosen maximum values, that are bounded and not necessarily null.
In this paper a systematic method, in a more general framework with respect to the ones proposed in literature (see e.g. [1-5,8-10,13-18]), for the analysis and for the practical stabilization of a significant class of MIMO uncertain pseudo-linear and pseudo-quadratic systems, with additional bounded nonlinearity and/or bounded disturbances, is considered. In detail, by using the concept of majorant system, via Lyapunov approach, new fundamental theorems, from which derive explicit formulas and efficient algorithms to design state feedback control laws, with a possible imperfect compensation of nonlinearities and disturbances, are stated. These results guarantee a specified convergence velocity of the linearized system of the majorant system and a desired steady-state output for generic uncertainties and/or generic bounded nonlinearities and/or bounded disturbances (see also [19-21]). Finally two significant examples of application, well showing the utility and the efficiency of the proposed results, are reported.
2. Problem Formulation and Preliminary Results
Consider the following class of uncertain quadratic multivariable systems
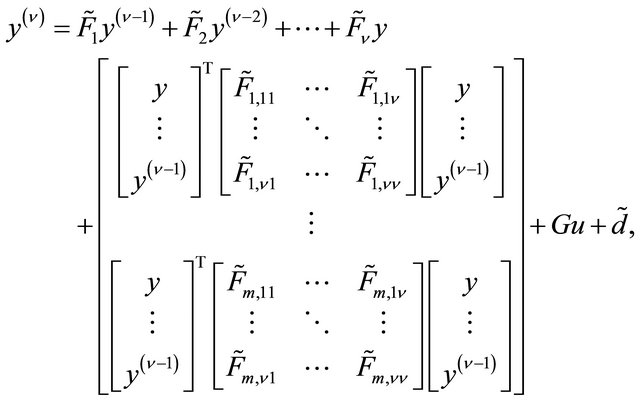 (1.1)
(1.1)
where: 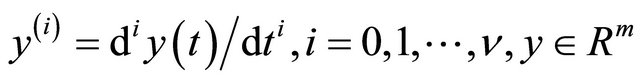 is the output,
is the output, 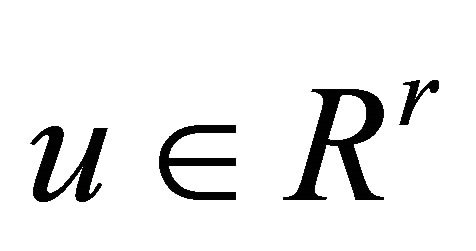 is the control input,
is the control input, 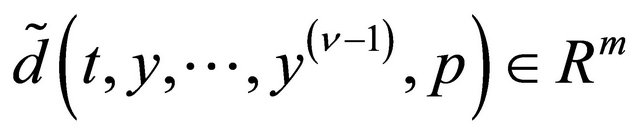 models possible external signals and/or particular nonlinearities of the system,
models possible external signals and/or particular nonlinearities of the system, 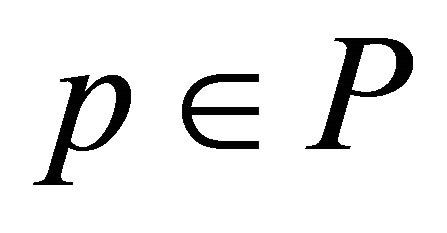 , with P a compact set of
, with P a compact set of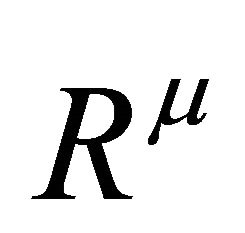 , is the vector of the uncertain parameters,
, is the vector of the uncertain parameters, 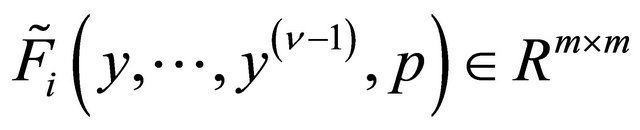 and
and
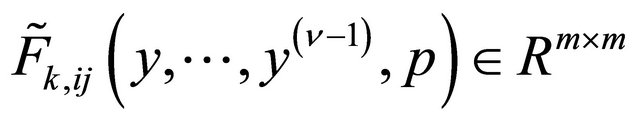 are bounded matrices, continuous with respect to their arguments,
are bounded matrices, continuous with respect to their arguments,
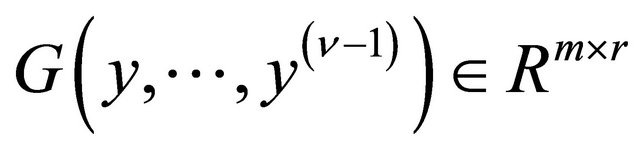 is a matrix continuous with respect to its arguments and with rank m.
is a matrix continuous with respect to its arguments and with rank m.
Now suppose that there exist the nominal values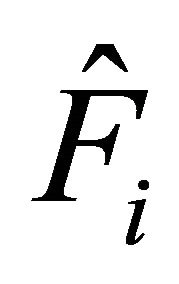 ,
, 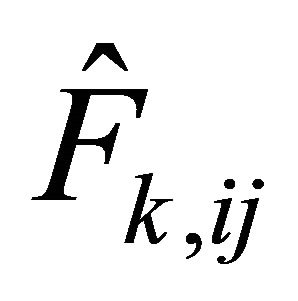 ,
, ![]() of
of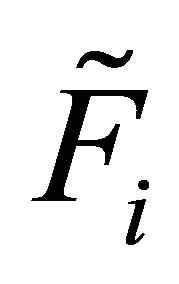 ,
, 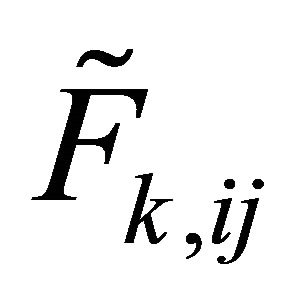 ,
, ![]() such that
such that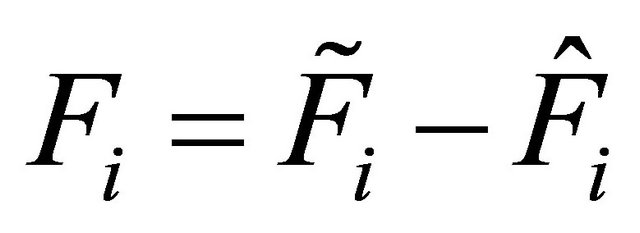 ,
,  are functions multilinear with respect to
are functions multilinear with respect to 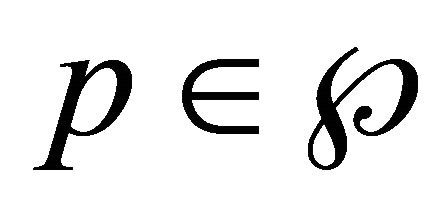 and with respect to bounded function
and with respect to bounded function 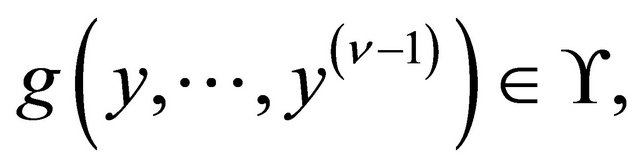 where
where

and 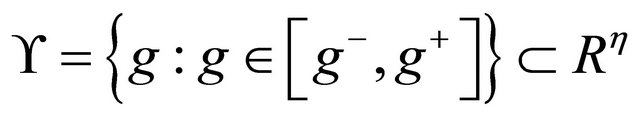 are hyper-rectanglesand such that
are hyper-rectanglesand such that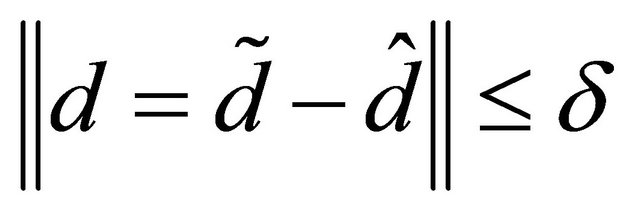 , where
, where ![]() is a constant.
is a constant.
Pose:
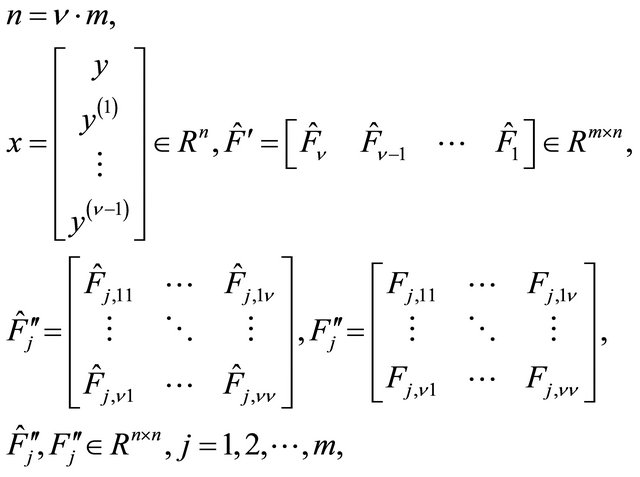 (1.2)
(1.2)
and denote with ,
,  , the matrices whose
, the matrices whose ![]() rows are respectively the i-th rows of the m matrices
rows are respectively the i-th rows of the m matrices 
Then, by controlling the system (1.1) with the following state feedback control law with a partial compensation
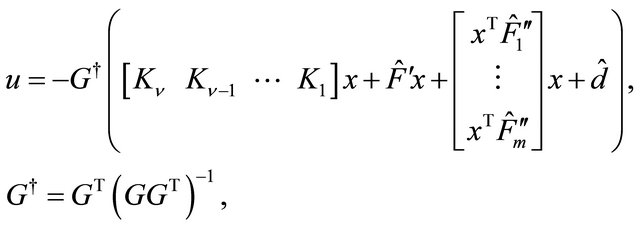 (1.3)
(1.3)
it is easy to verify that the closed-loop system turns out to be
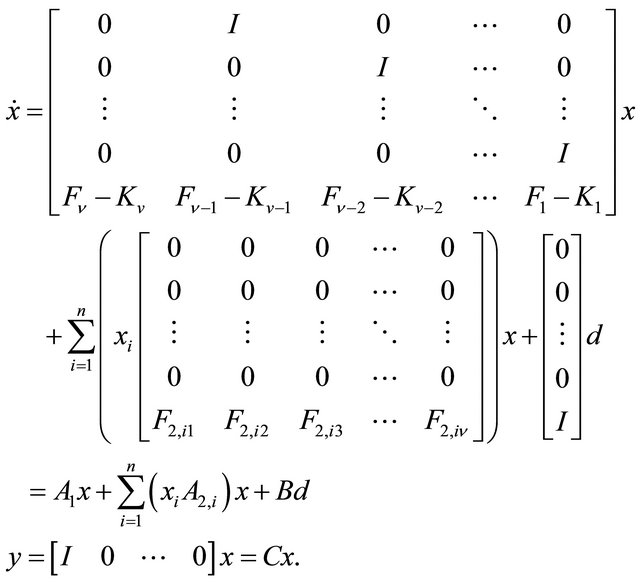 (1.4)
(1.4)
To develop a practical stabilization method for the system (1.4), in a more systematic and general framework, which allows to calculate in a simple manner a control law that guarantees a specified convergence velocity, the following notations, definitions and preliminary results are provided.
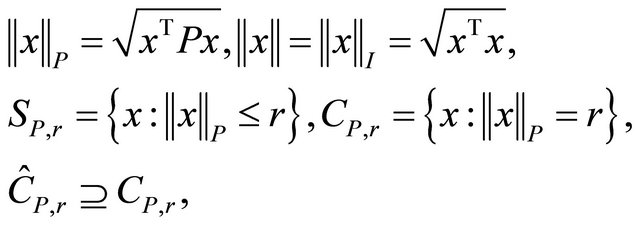 (1.5)
(1.5)
where 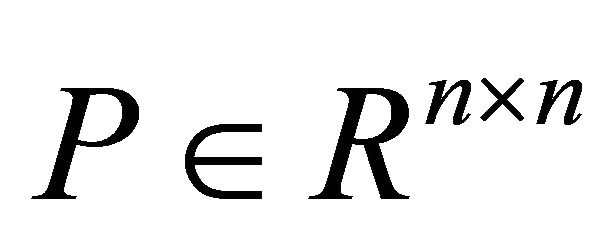 is a symmetric and positive definite
is a symmetric and positive definite 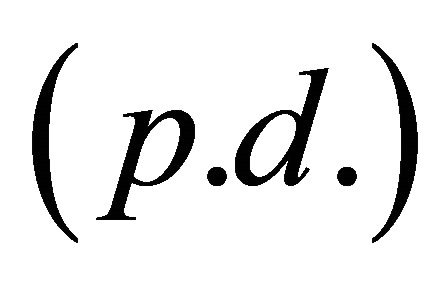 matrix and
matrix and 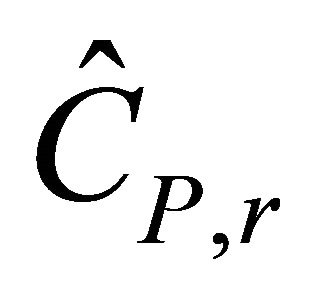 is a compact set.
is a compact set.
Definition 1. Give the system (1.4) and a 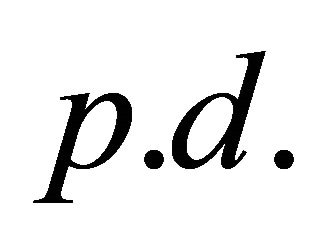 symmetric matrix
symmetric matrix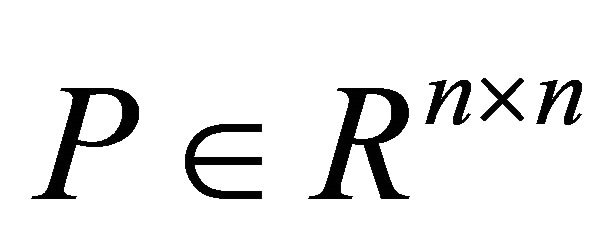 . A first-order positive system
. A first-order positive system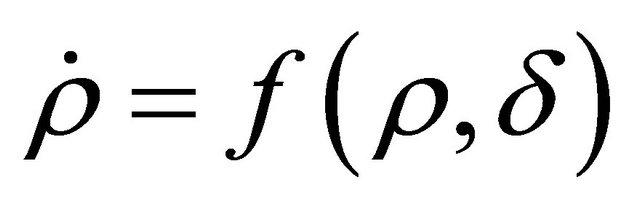 ,
, 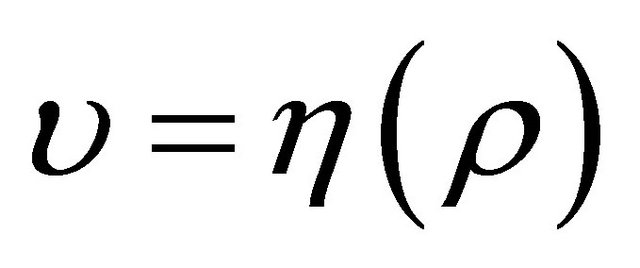 , where
, where 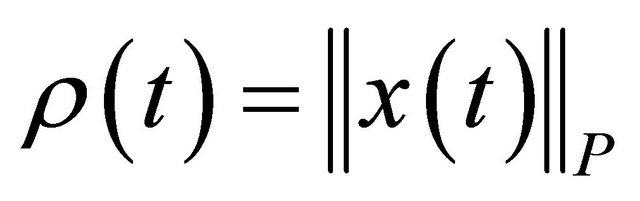 and
and  such that
such that 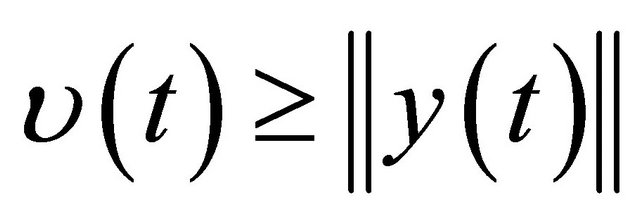 is said to be majorant system of the system (1.4).
is said to be majorant system of the system (1.4).
Theorem 1. Consider the quadratic system
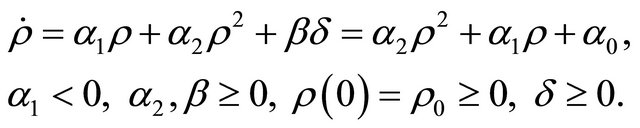 (1.6)
(1.6)
If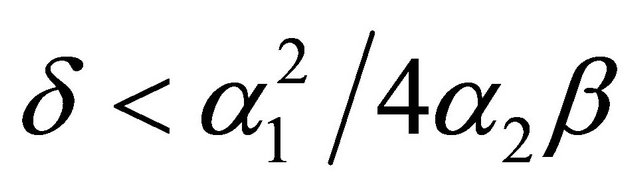 , it is (see Figure 1)
, it is (see Figure 1)

Figure 1. Graphical representation of the system (1.6).
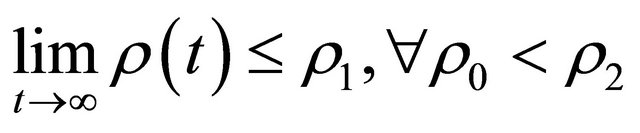 , (1.7)
, (1.7)
where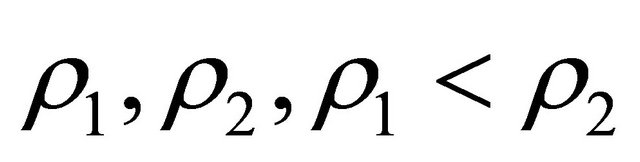 , are the roots of the algebraic equation
, are the roots of the algebraic equation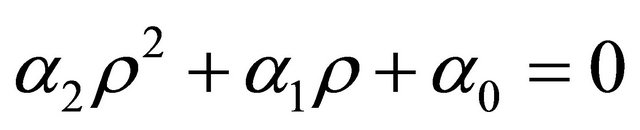 . Moreover for
. Moreover for 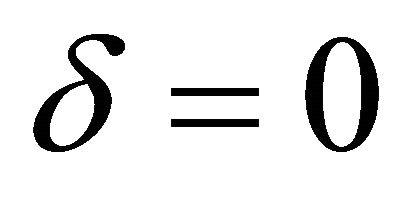 the practical convergence time
the practical convergence time  is given by (see Figure 2)
is given by (see Figure 2)
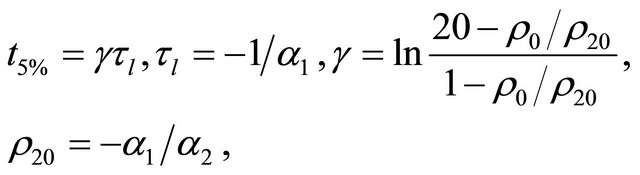 (1.8)
(1.8)
in which ![]() is the time constant of the linearized of the system (1.6) and
is the time constant of the linearized of the system (1.6) and 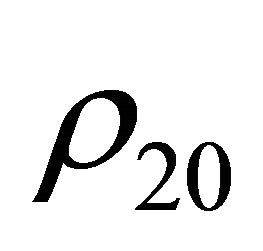 is the upper bound of the convergence interval of
is the upper bound of the convergence interval of 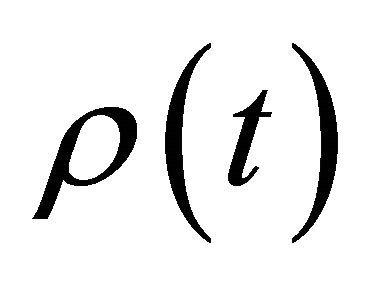 for
for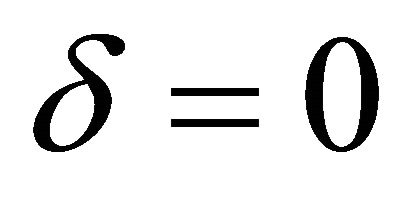 , i.e. of the system (1.6) in free evolution.
, i.e. of the system (1.6) in free evolution.
Proof. The proof of (1.7) easily follows from Figure 1. Instead (1.8) easily derives by noting that the solution of (1.6) for 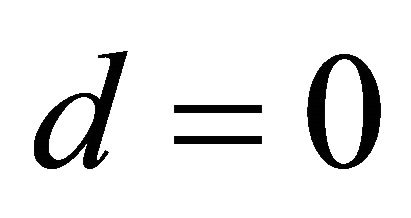 is
is
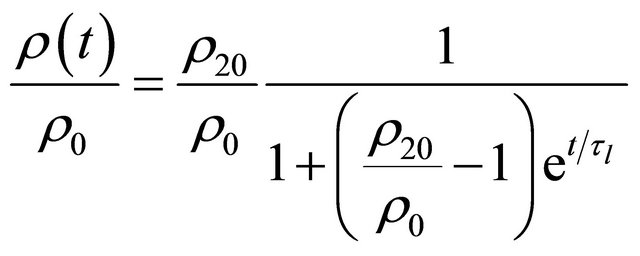 . (1.9)
. (1.9)
In Figure 2 the evolution of 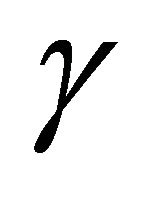 as a function of
as a function of 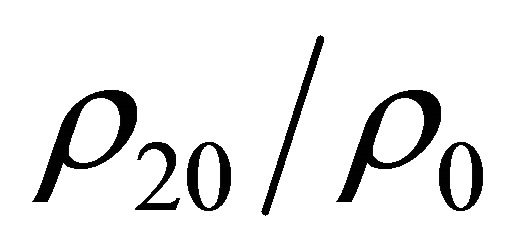 is reported. By analyzing Figure 2, note that for
is reported. By analyzing Figure 2, note that for 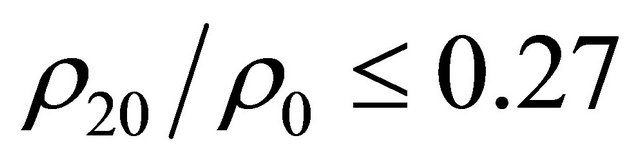 it is
it is 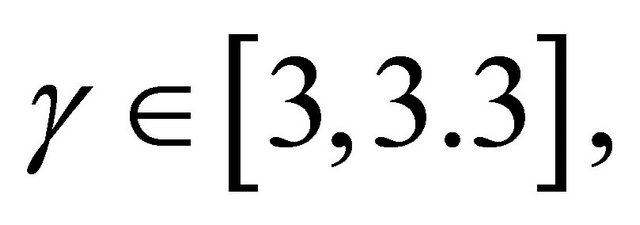 i.e.
i.e.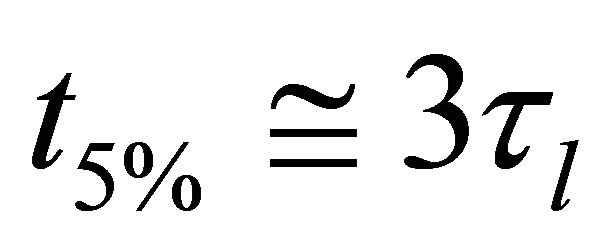 .
.
Theorem 2. The solution of the Equation (1.6) with 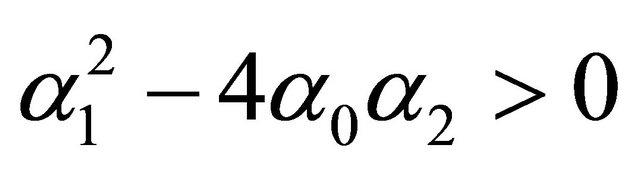 is
is
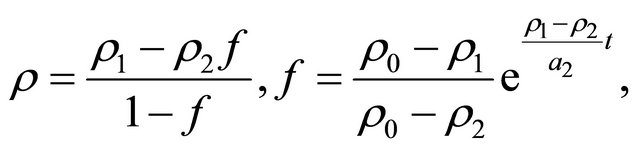 (1.10)
(1.10)
where , are the roots of the equation
, are the roots of the equation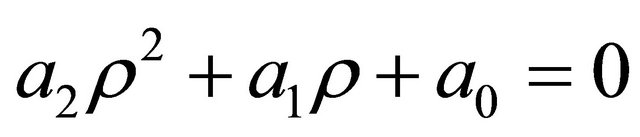 .
.
Proof. From (1.6) it derives
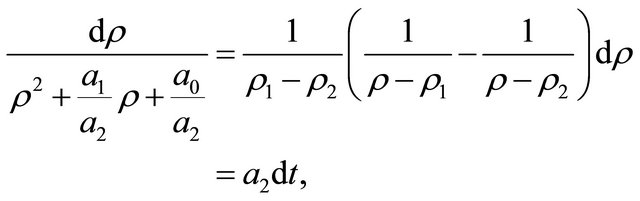 (1.11)
(1.11)
from which (1.10) easily follows.
Lemma 1. If 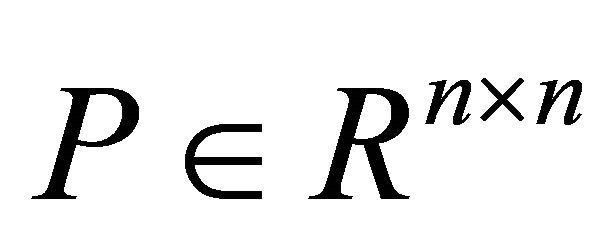 is a symmetric and p.d. matrix,
is a symmetric and p.d. matrix, 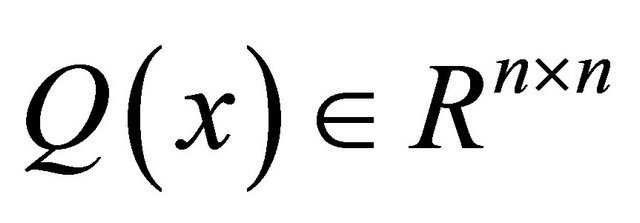 is a symmetric matrix, continuous with respect to
is a symmetric matrix, continuous with respect to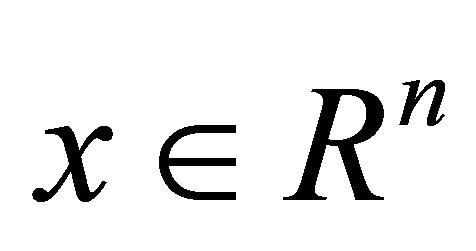 , and
, and 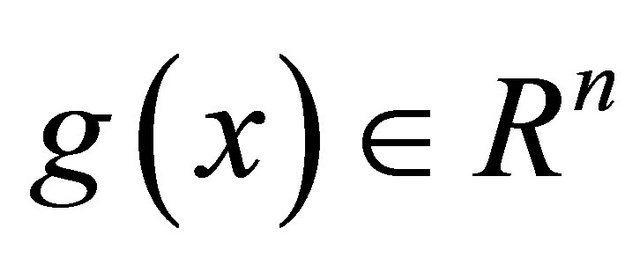 is continuous with respect to
is continuous with respect to![]() , then
, then 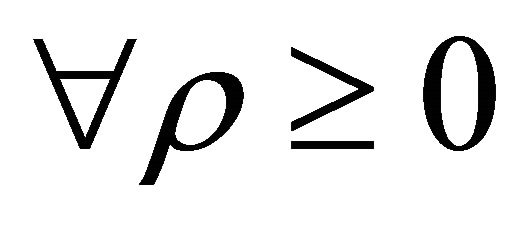 it is:
it is:

Figure 2. Factor γ as a function of the normalized initial condition.
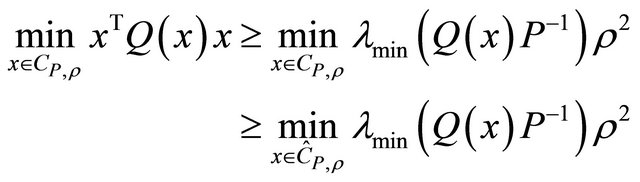 (1.12)
(1.12)
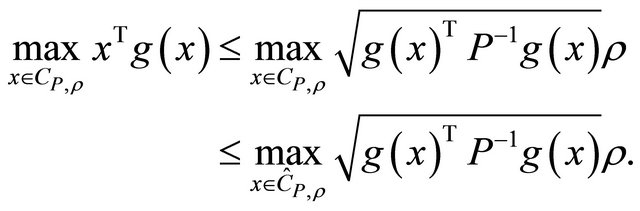 (1.13)
(1.13)
Moreover, if 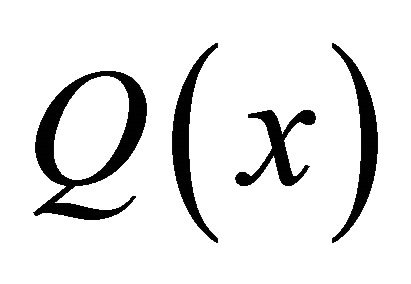 is linear with respect to x it is
is linear with respect to x it is
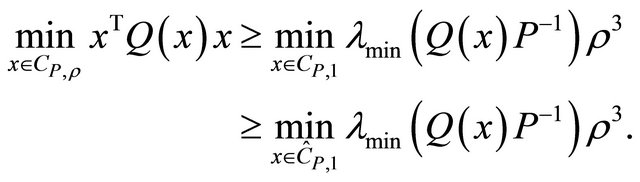 (1.14)
(1.14)
More in general, if 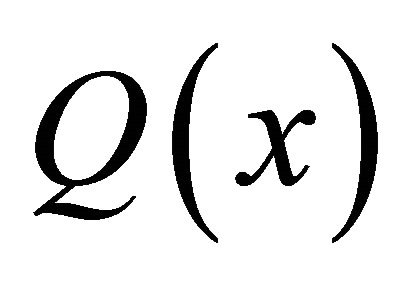 is pseudo-linear with respect to x with bounded coefficients, i.e. if
is pseudo-linear with respect to x with bounded coefficients, i.e. if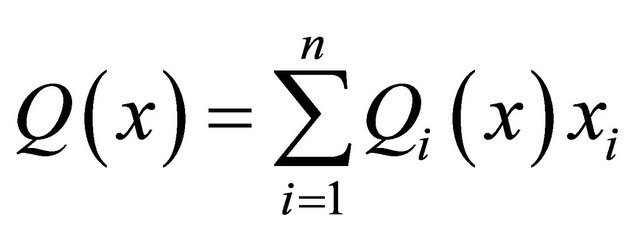 where
where 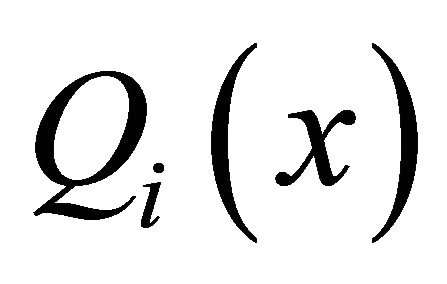 are bounded, then
are bounded, then
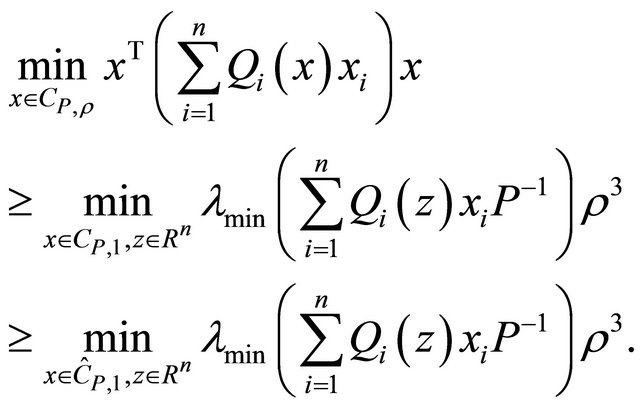 (1.15)
(1.15)
Proof. Note that, if  is a continuous function with respect to
is a continuous function with respect to 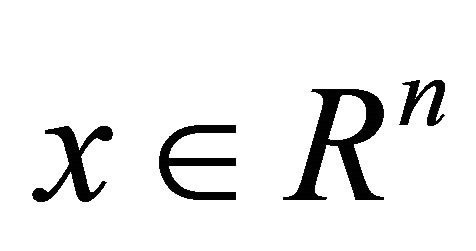 and
and 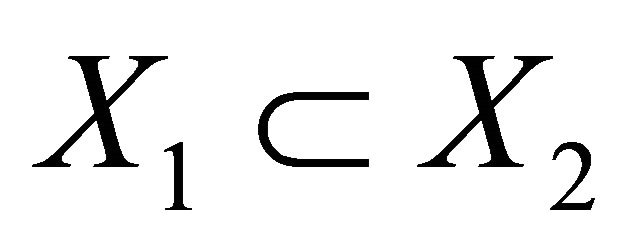 are compact subsets of
are compact subsets of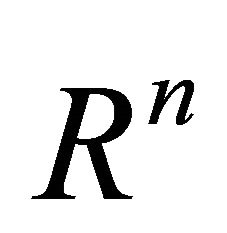 , it is
, it is ,
,
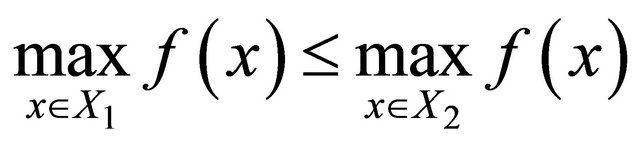 . Moreover, since P is p.d., there exists a symmetric nonsingular matrix
. Moreover, since P is p.d., there exists a symmetric nonsingular matrix ![]() such that
such that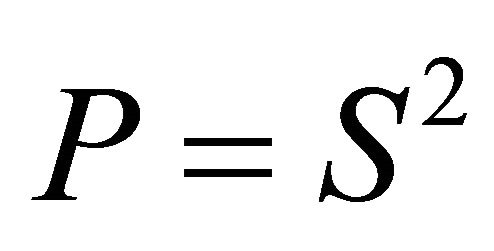 . Hence, by posing
. Hence, by posing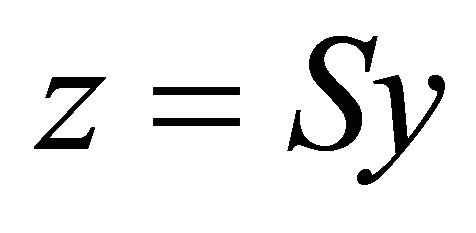 , it is
, it is
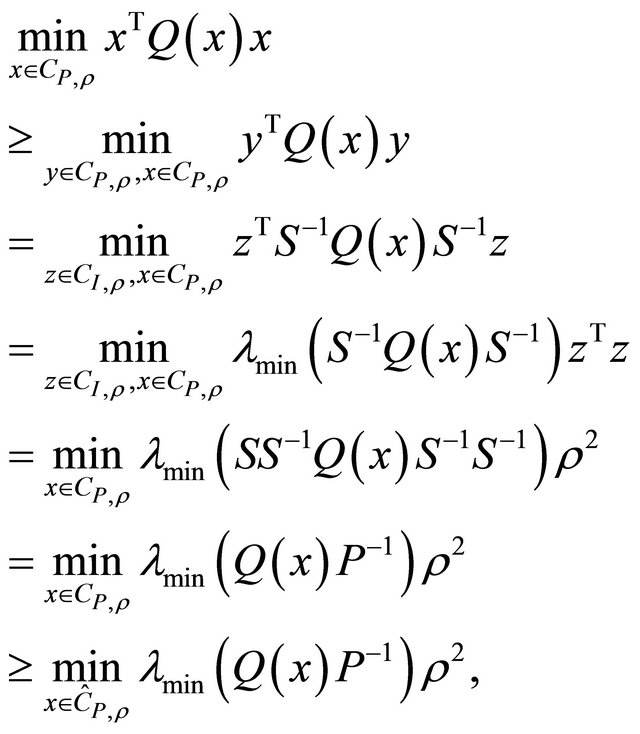 (1.16)
(1.16)
and so (1.12) holds. Similarly
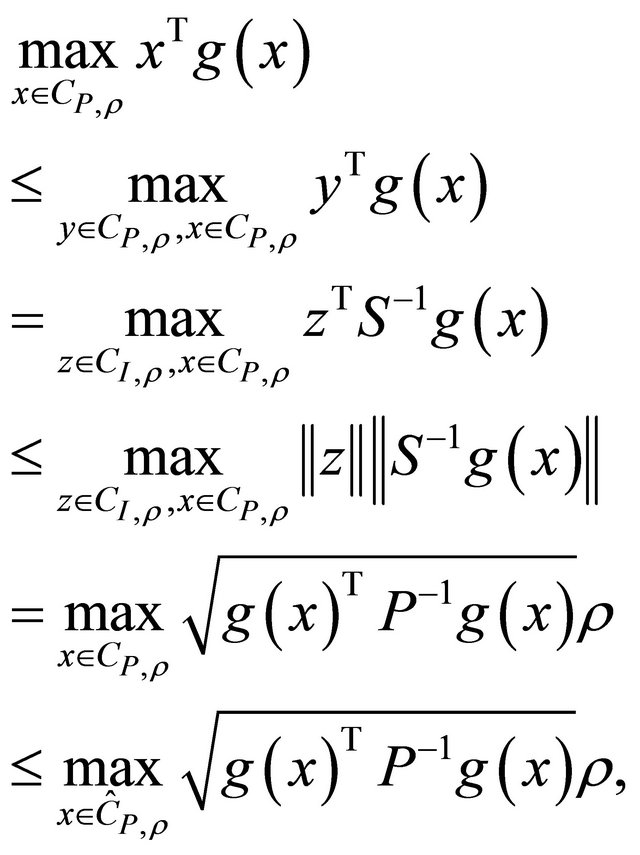 (1.17)
(1.17)
and hence (1.13). The inequalities (1.14) easily follow from the fact that, if 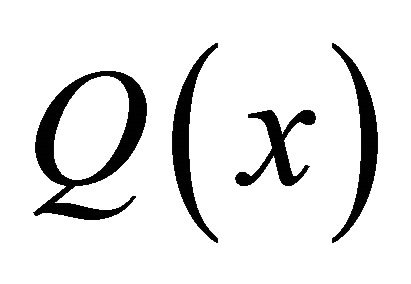 is linear with respect to
is linear with respect to![]() ,
,
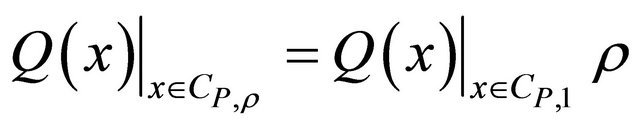 . The inequalities (1.15) analogously follow.
. The inequalities (1.15) analogously follow.
Remark 1. Clearly, if 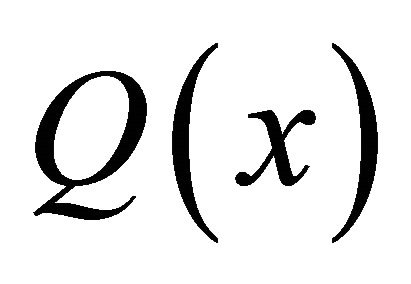 and
and 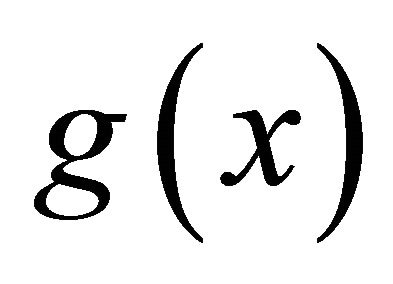 are independent of
are independent of![]() , (1.12) and (1.13) are valid with the equal sign. If
, (1.12) and (1.13) are valid with the equal sign. If 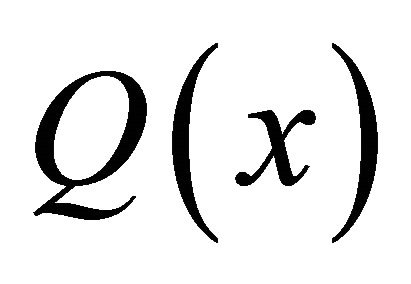 depends on x,
depends on x, 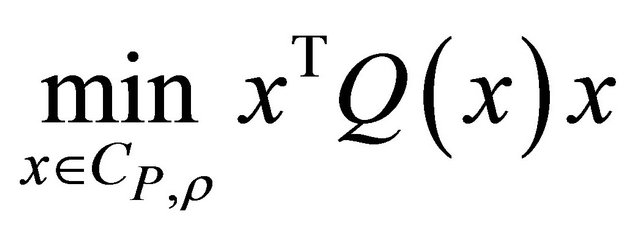 is quite difficult to compute because
is quite difficult to compute because 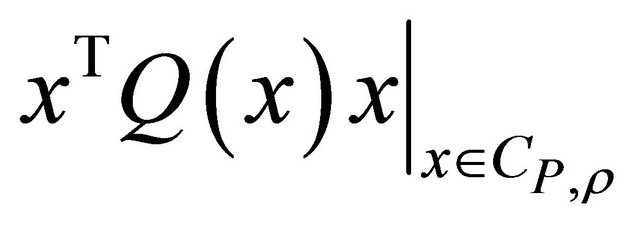 has in general different points of relative maximum, of relative minimum and of “inflection”; moreover, the second and the third member of (1.12) (of (1.14) or of (1.15)) allow an easier computation of a lower bound on
has in general different points of relative maximum, of relative minimum and of “inflection”; moreover, the second and the third member of (1.12) (of (1.14) or of (1.15)) allow an easier computation of a lower bound on
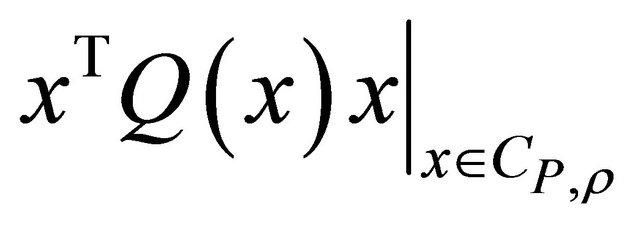 proportional to
proportional to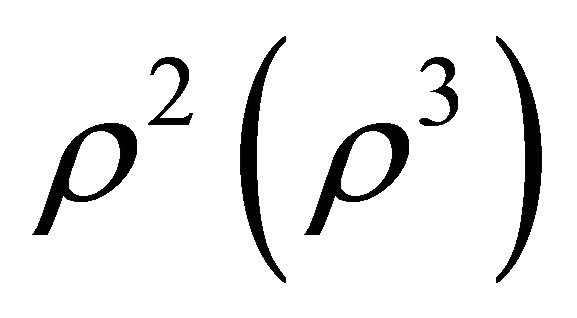 , as it will be shown later on. A similar talking is valid if
, as it will be shown later on. A similar talking is valid if 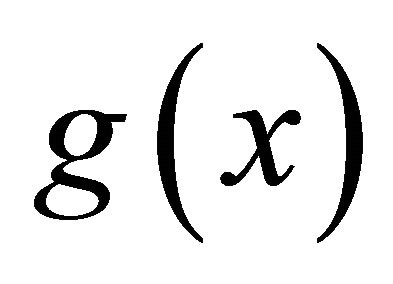 depends on
depends on![]() .
.
Lemma 2. Consider a p.d. matrix 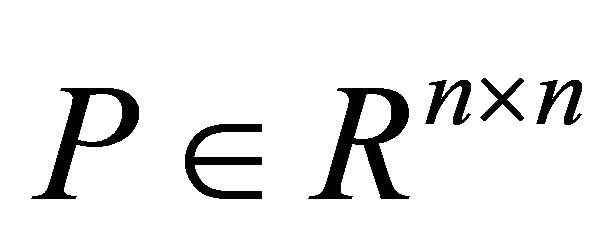 and a matrix
and a matrix 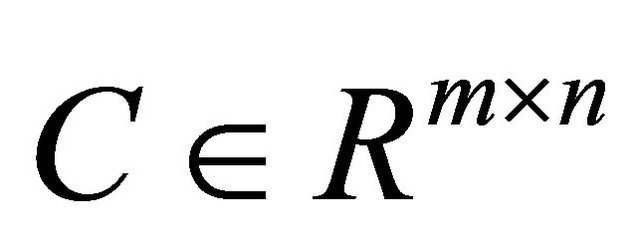 with rank m. If
with rank m. If 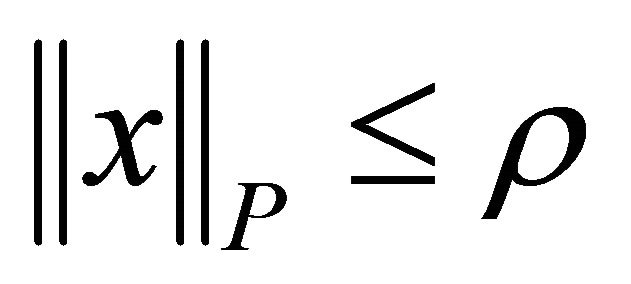 then the smallest
then the smallest ![]() such that
such that 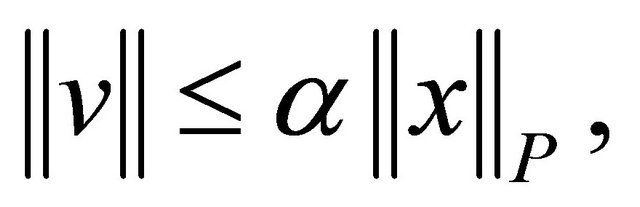 where
where 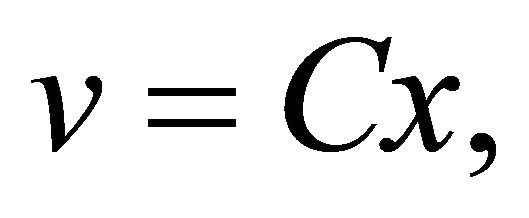 is equal to
is equal to 
Proof. Since P is p.d., by posing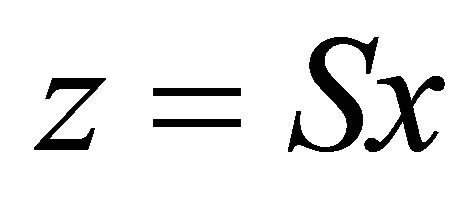 , where
, where ![]() is a symmetric nonsingular matrix such that
is a symmetric nonsingular matrix such that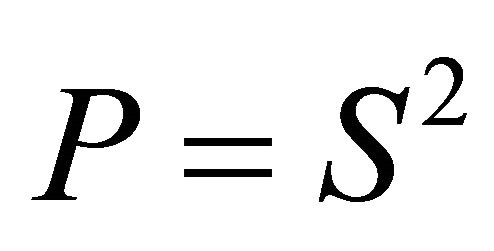 , then, in an equivalent way, the smallest
, then, in an equivalent way, the smallest ![]() such that
such that
 is also the smallest
is also the smallest ![]() such that the matrix
such that the matrix 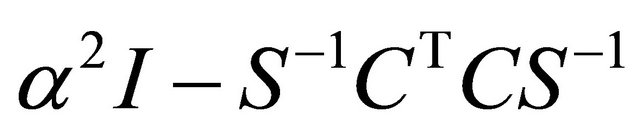 is positive semidefinite, i.e. all its eigenvalues are non-negative. As
is positive semidefinite, i.e. all its eigenvalues are non-negative. As
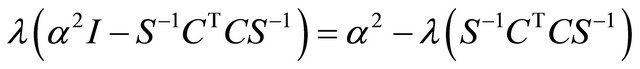 it is
it is 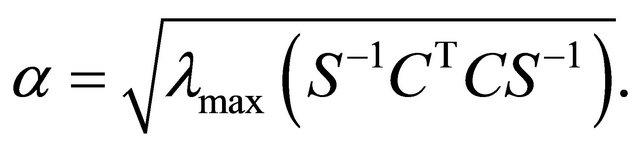 By taking into account that, if
By taking into account that, if  is a real
is a real ![]() matrix with rank
matrix with rank![]() , the matrix
, the matrix 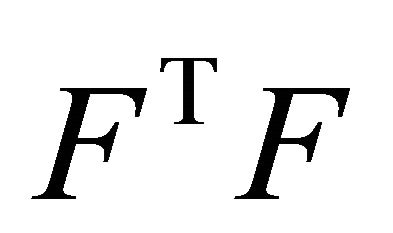 has
has ![]() null eigenvalues and
null eigenvalues and ![]() positive eigenvalues equal to the ones of
positive eigenvalues equal to the ones of 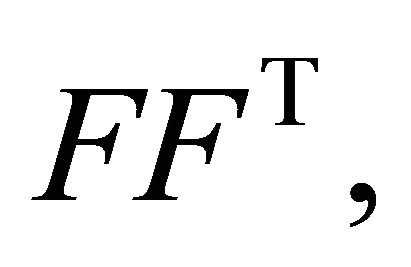 it follows that
it follows that
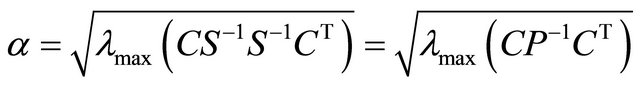 and, hence, the proof.
and, hence, the proof.
Lemma 3. Let 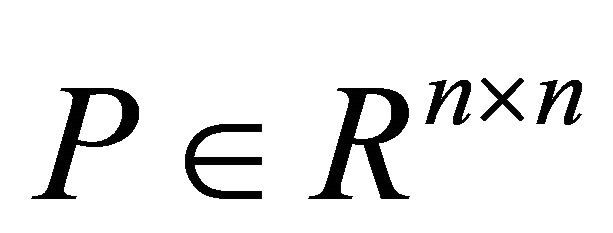 be a symmetric p.d. matrix with its inverse
be a symmetric p.d. matrix with its inverse 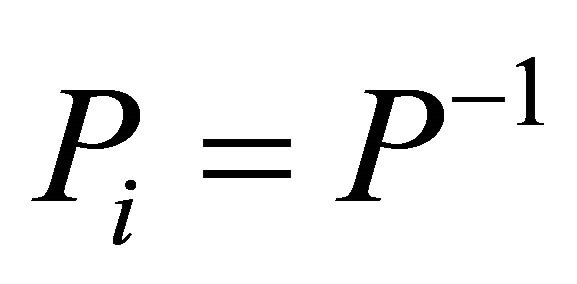 having unitary elements on the main diagonal. Then the hyper-rectangle of
having unitary elements on the main diagonal. Then the hyper-rectangle of 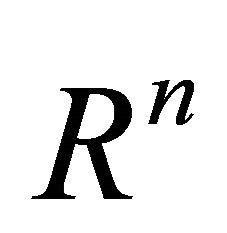 externally tangent to the hyper-ellipse
externally tangent to the hyper-ellipse 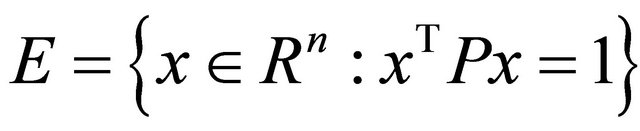 is the hyper-quadrilateral (quadrangle if
is the hyper-quadrilateral (quadrangle if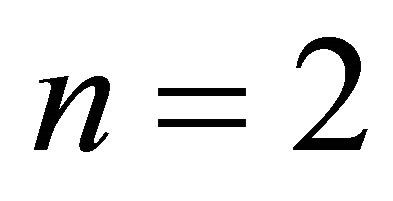 , cube if
, cube if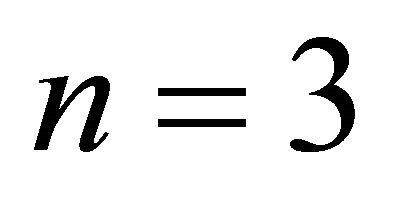 ) having as origin the centre and with unitary half-side.
) having as origin the centre and with unitary half-side.
Proof. It is easy to prove that the point of contact of the hyper-line orthogonal to the versor 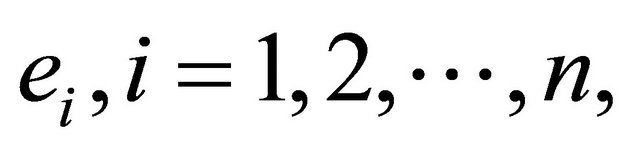 of
of 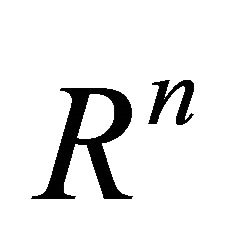 and tangent to the hyper-ellipse E is
and tangent to the hyper-ellipse E is
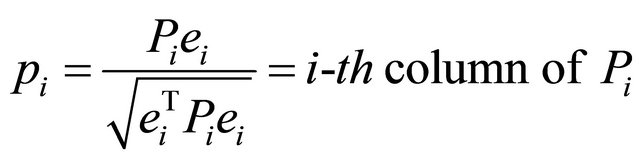 . (1.18)
. (1.18)
From this the proof easily follows.
The following significant and useful theorem is stated.
Theorem 3. Let

be a matrix multilinearly depending on the parameters

and let 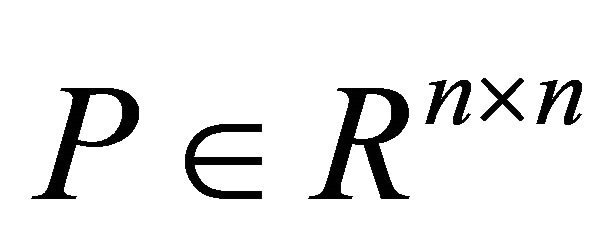 be a symmetric p.d. matrix. Then the minimum (maximum) of
be a symmetric p.d. matrix. Then the minimum (maximum) of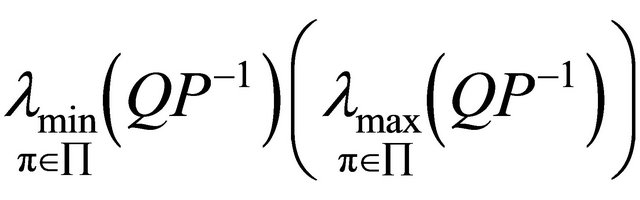 , where
, where
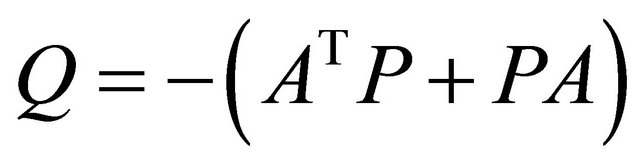 , is attained in one of the
, is attained in one of the 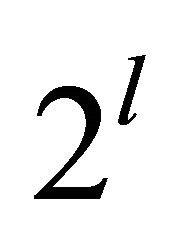 vertices of
vertices of .
.
Proof. Note that for a constant  it is
it is 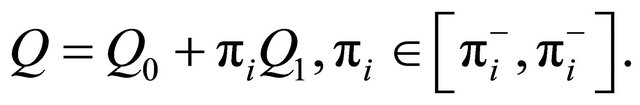 Moreover, by taking into account that
Moreover, by taking into account that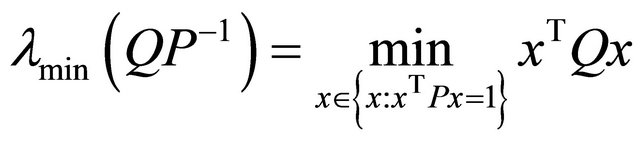 , it turns out to be that
, it turns out to be that
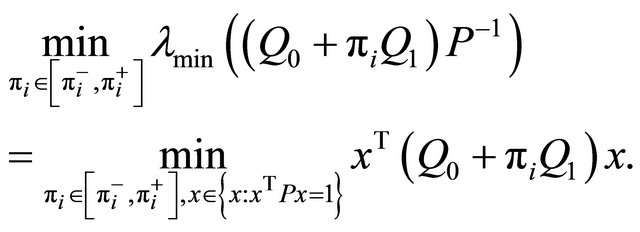 (1.19)
(1.19)
Therefore, said  the points of minimum of
the points of minimum of
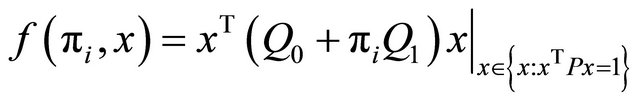 , it is
, it is
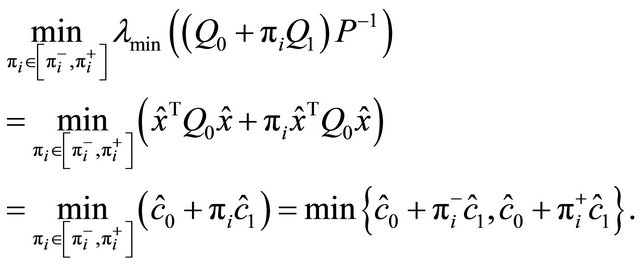 (1.20)
(1.20)
From (1.20) the proof easily follows.
3. Main Result
Now the first main result, concerning the analysis of stability, can be stated.
Theorem 4. Give a symmetric p.d. matrix . Then a majorant system of the system (1.4) is
. Then a majorant system of the system (1.4) is
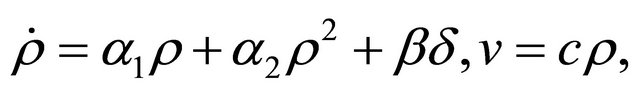 (1.21)
(1.21)
in which:
 (1.22)
(1.22)
where 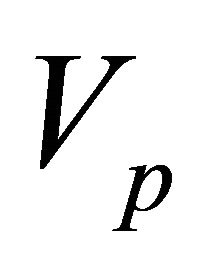 and
and 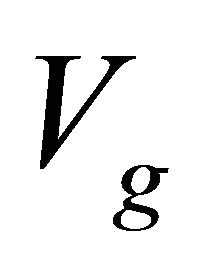 are the sets of vertices of the hyperrectangle
are the sets of vertices of the hyperrectangle  and of the hyper-rectangle
and of the hyper-rectangle ![]() respectively, and
respectively, and  is the set of vertices of the hyper-rectangle of
is the set of vertices of the hyper-rectangle of 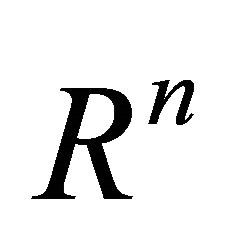 externally tangent to the hyper-ellipse
externally tangent to the hyper-ellipse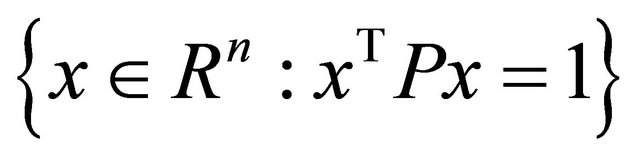 .
.
Proof. By choosing as “Lyapunov function” the quadratic form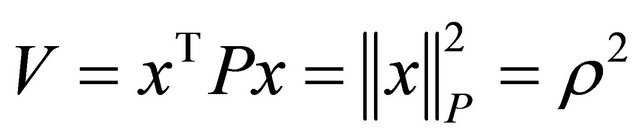 , for x belonging to a generic hyper-circumference
, for x belonging to a generic hyper-circumference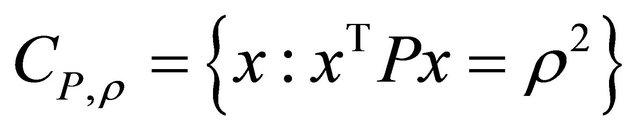 , it is
, it is
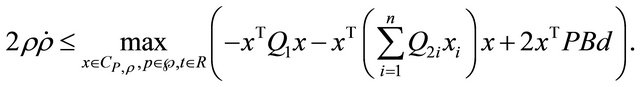 (1.23)
(1.23)
The proof easily follows from (1.23), Lemmas 1, 2 and Theorem 3.
The second main result, concerning the synthesis of the stabilizing control law, follows from Theorem 4.
Theorem 5.
Let 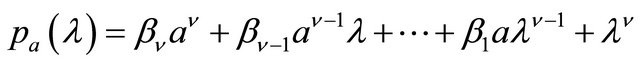 be the characteristic polynomial of the low-pass Butterworth filter of order
be the characteristic polynomial of the low-pass Butterworth filter of order ![]() with cutoff frequency
with cutoff frequency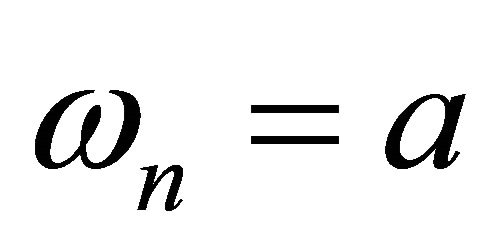 .
.
If in (1.3) it is posed
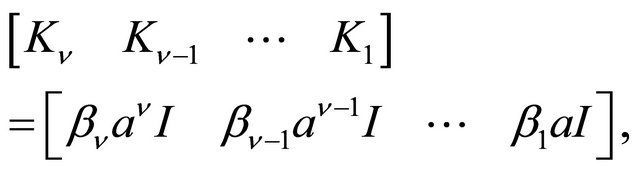 (1.24)
(1.24)
in which I is the identity matrix of order m, then a majorant system of the system (1.4) with respect to the norm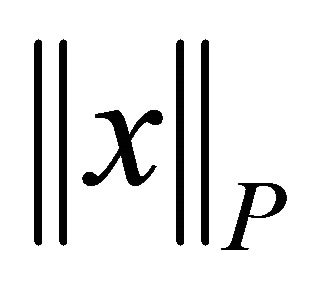 , with
, with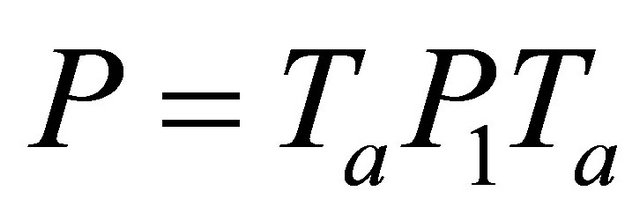 , where
, where
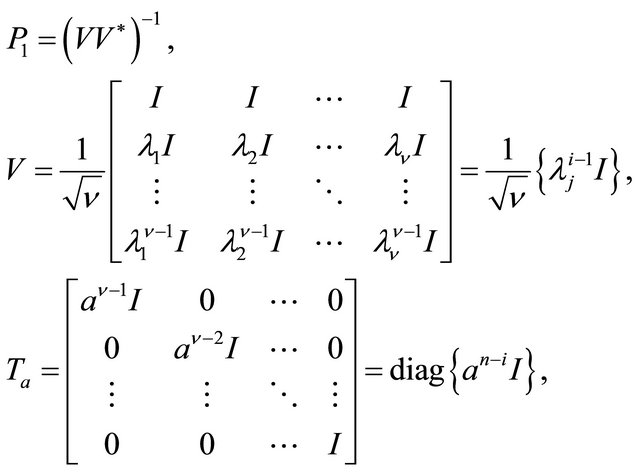 (1.25)
(1.25)
being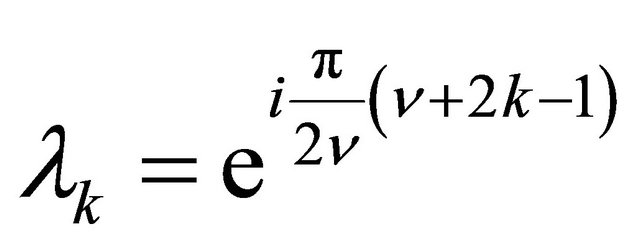 ,
, 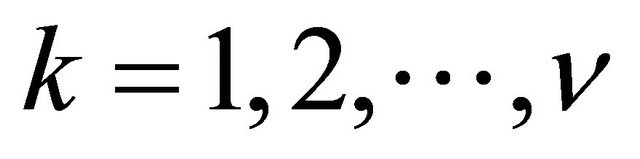 , the k-th root of
, the k-th root of 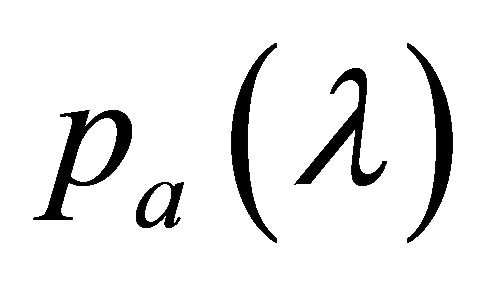 for
for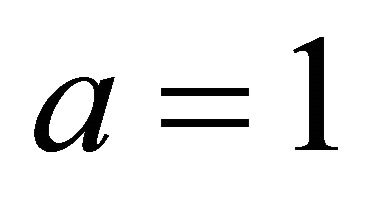 , is
, is
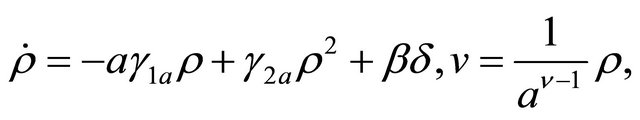 (1.26)
(1.26)
in which:
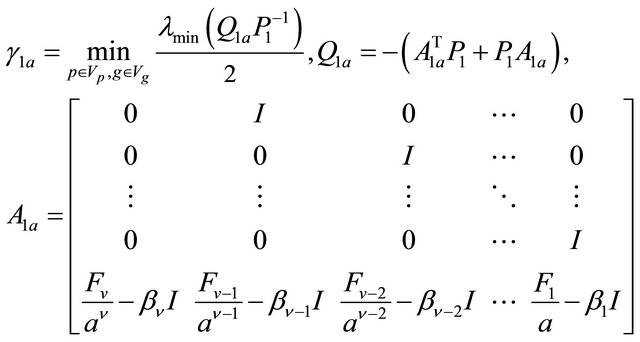 (1.27)
(1.27)
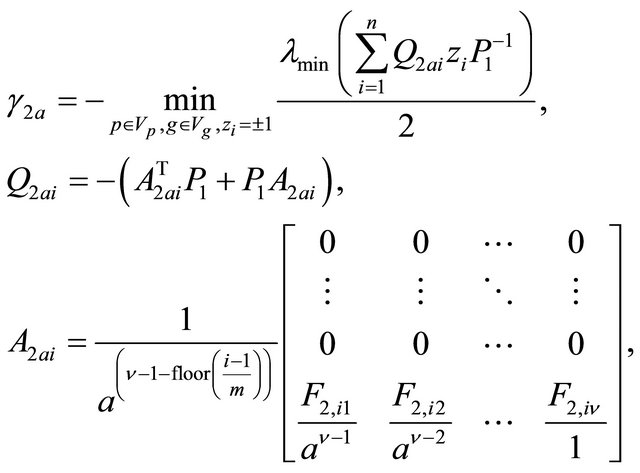 (1.28)
(1.28)
 (1.29)
(1.29)
Proof. By making the change of variable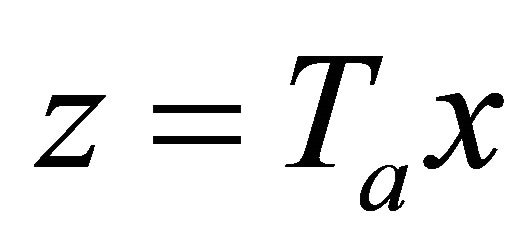 , it is easy to prove that the system (1.4) becomes
, it is easy to prove that the system (1.4) becomes
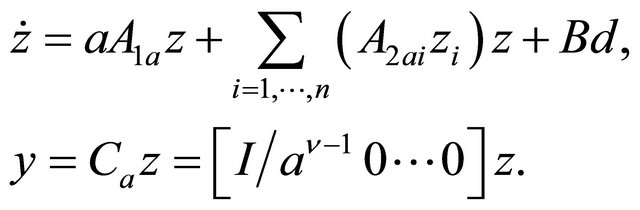 (1.30)
(1.30)
Moreover, note that the Butterworth eigenvalues 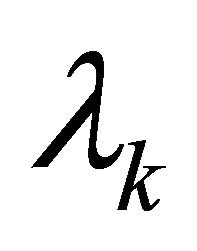 have unitary magnitudes; hence all the main diagonal elements of the matrix
have unitary magnitudes; hence all the main diagonal elements of the matrix 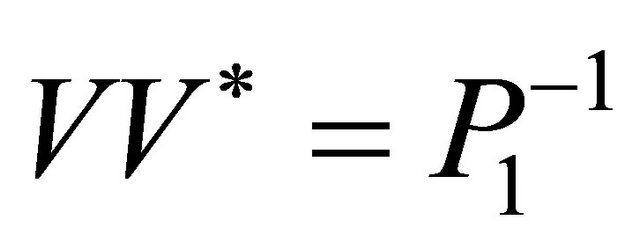 are unitary. From this consideration, from (1.30), from Lemmas 2, 3 and Theorem 4, the proof easily follows.
are unitary. From this consideration, from (1.30), from Lemmas 2, 3 and Theorem 4, the proof easily follows.
Theorem 6. For![]() , the parameters
, the parameters 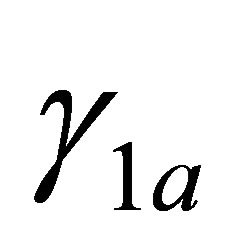 and
and 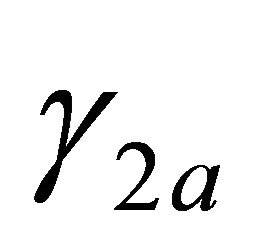 of the majorant system (1.26) turn out to be
of the majorant system (1.26) turn out to be
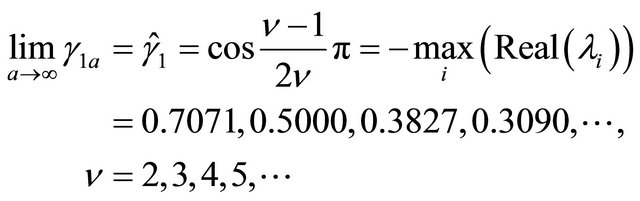 (1.31)
(1.31)
 (1.32)
(1.32)
Proof. It is easy to verify that for ![]() the matrix
the matrix 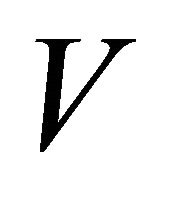 is the limit of the eigenvectors matrix of the matrix
is the limit of the eigenvectors matrix of the matrix 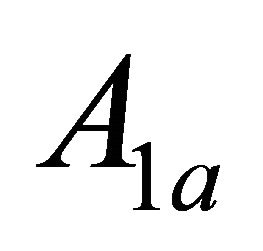 (see (1.27)); hence it is that
(see (1.27)); hence it is that ,
,
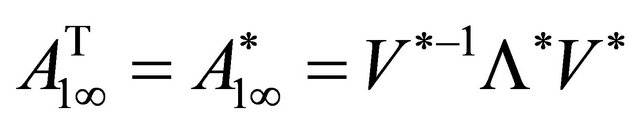 , where
, where
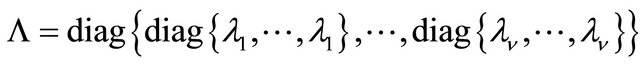 . Therefore
. Therefore
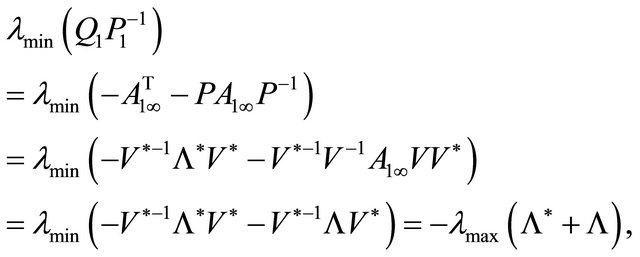 (1.33)
(1.33)
hence (1.31).
Moreover it is easy to verify that
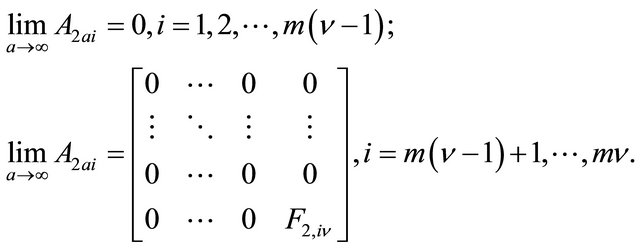 (1.34)
(1.34)
From (1.28) and (1.34) the expression (1.32) easily follows.
Remark 2. If 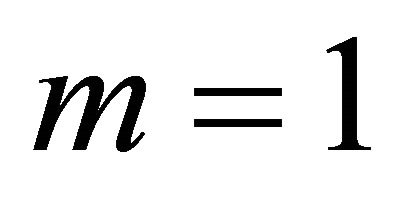 it is easy to prove that
it is easy to prove that
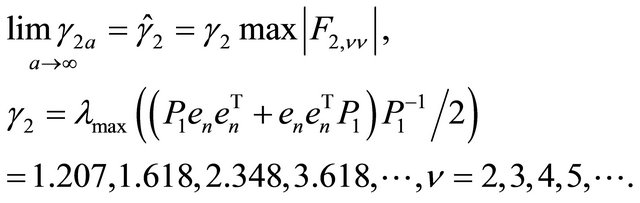 (1.35)
(1.35)
From Theorems 5 and 6 the following result derives.
Theorem 7. Consider the system (1.4) with
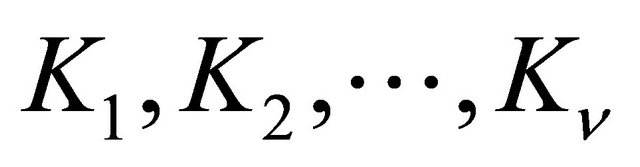 provided from (1.24). If the design parameter a is big enough, from a practical point of view, the time constant
provided from (1.24). If the design parameter a is big enough, from a practical point of view, the time constant ![]() of the linearized of the majorant system (1.26) is inverse proportional to a and it coincides with the maximum time constant of the linearized of the system (1.4). More in detail, if a is large enough it turns out to be
of the linearized of the majorant system (1.26) is inverse proportional to a and it coincides with the maximum time constant of the linearized of the system (1.4). More in detail, if a is large enough it turns out to be
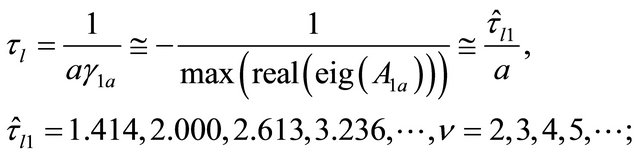 (1.36)
(1.36)
moreover, if a is sufficiently large, for t large enough it is
 (1.37)
(1.37)
or, more in general, it is
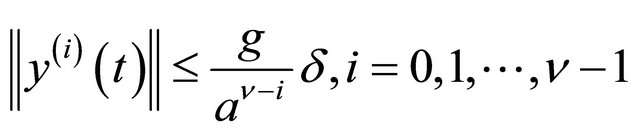 . (1.38)
. (1.38)
Proof. (1.36) easily follows from (1.26), (1.31) and by noting that
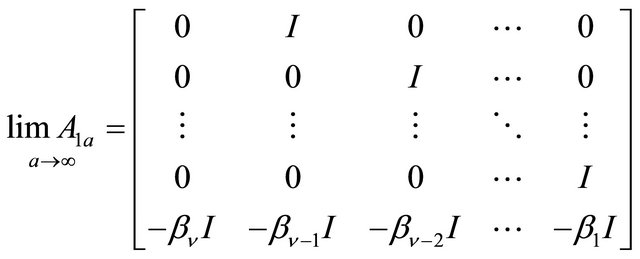 . (1.39)
. (1.39)
The inequality (1.37) follows from (1.7), from the fact that if a is sufficiently large then 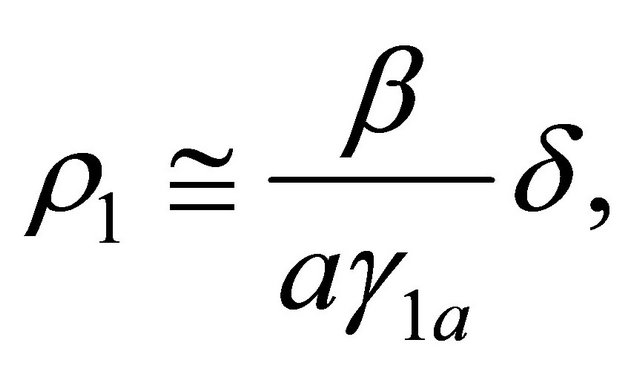 from the second of (1.26) and from (1.29) and (1.31).
from the second of (1.26) and from (1.29) and (1.31).
(1.38) analogously follows by taking into account that
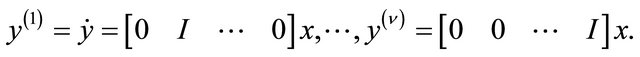 (1.40)
(1.40)
4. Examples
The following examples show the utility and the efficiency of the results stated in the previous sections.
Example 1. Consider the pseudo-linear uncertain system
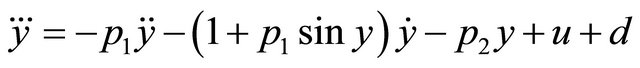 , (1.41)
, (1.41)
where  and
and 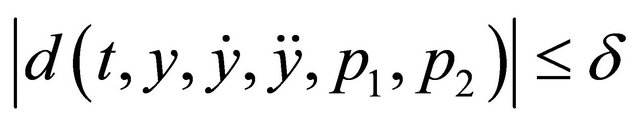 . By posing
. By posing 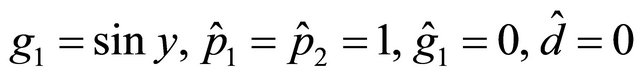 and by applying Theorem 5, the majorant system of the system (1.41) controlled with the control law
and by applying Theorem 5, the majorant system of the system (1.41) controlled with the control law
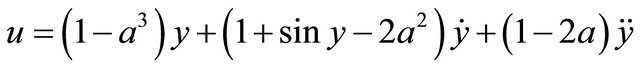 turns out to be
turns out to be
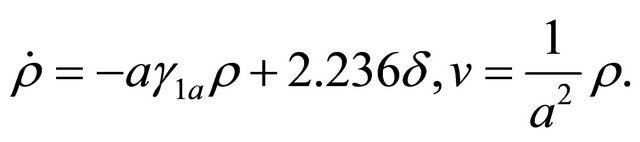 (1.42)
(1.42)
In Figure 3 the value of  for
for  is reported. It is significant to note that for
is reported. It is significant to note that for 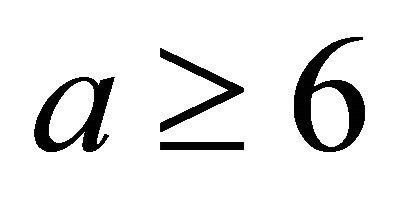 it is
it is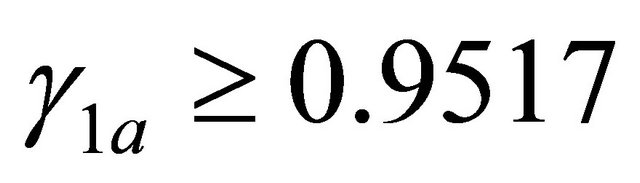 , i.e.
, i.e. 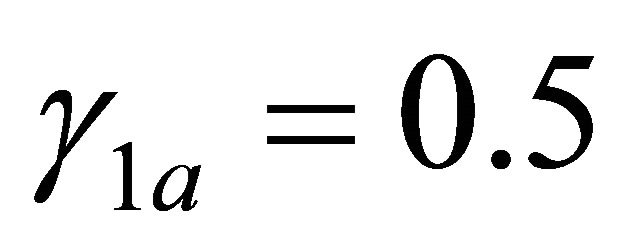 unless 5%, in accord with Theorem 7. For
unless 5%, in accord with Theorem 7. For 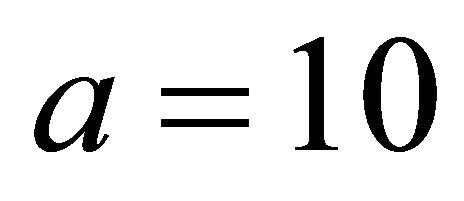 it is
it is 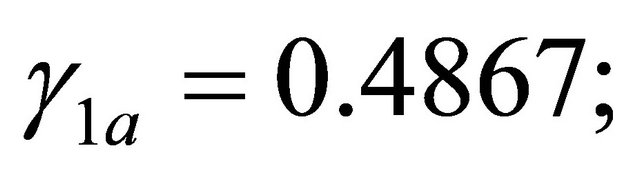 hence
hence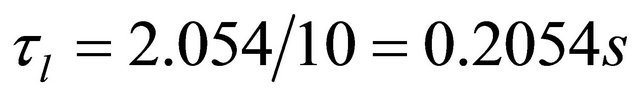 . Moreover, being
. Moreover, being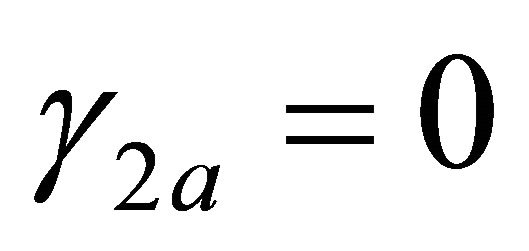 , it is
, it is  and
and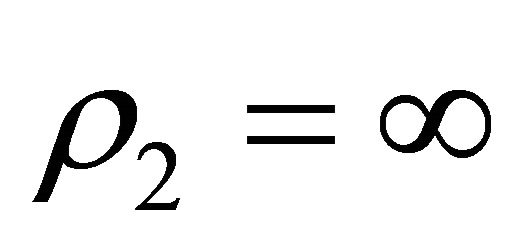 . Therefore, at “steady state”,
. Therefore, at “steady state”, 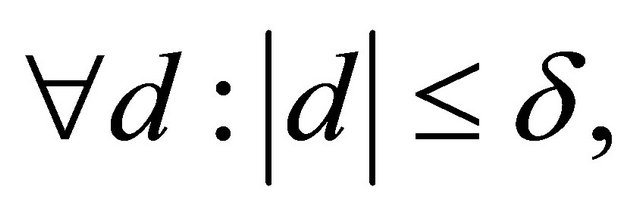 it is:
it is:
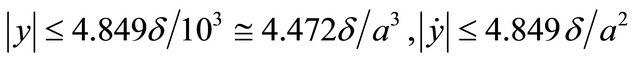 and
and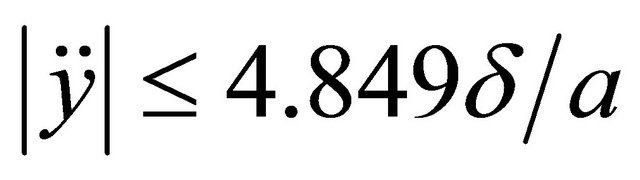 .
.
Example 2. Consider the system of Figure 4 described by the equation
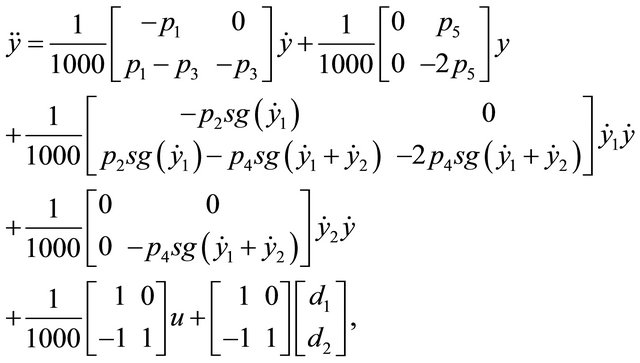 (1.43)
(1.43)
in which 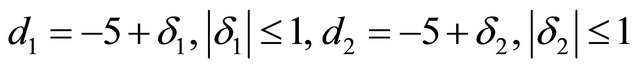 are the disturbance actions due to several causes included the slope of the road,
are the disturbance actions due to several causes included the slope of the road, 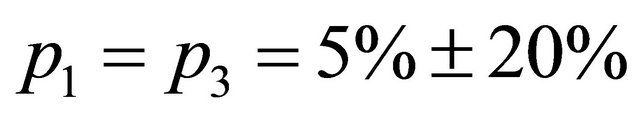 ,
, 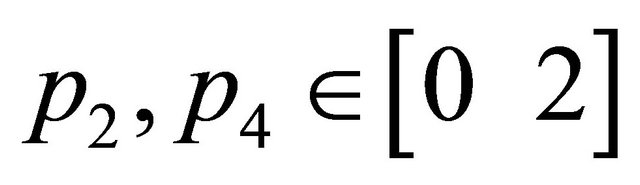 ,
, 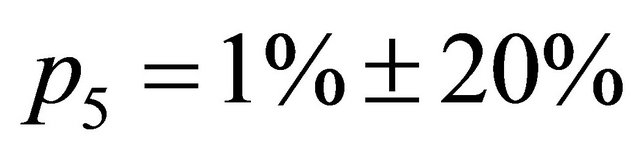 and
and

By posing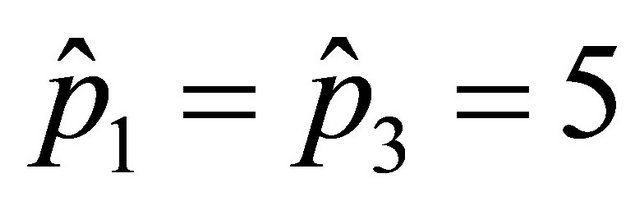 ,
, 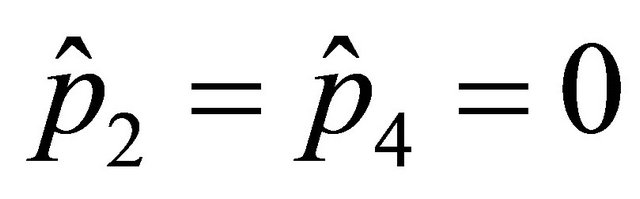 ,
,  ,
,
 and by applying Theorem 5 the majorant
and by applying Theorem 5 the majorant
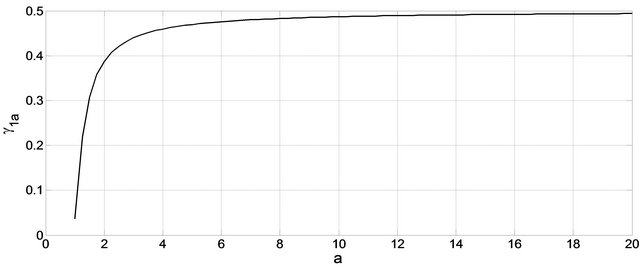
Figure 3. γ1a as a function of a.
system of (1.43), controlled by using the control law
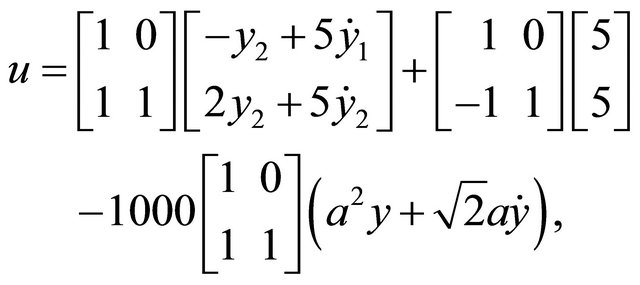 (1.44)
(1.44)
turns out to be
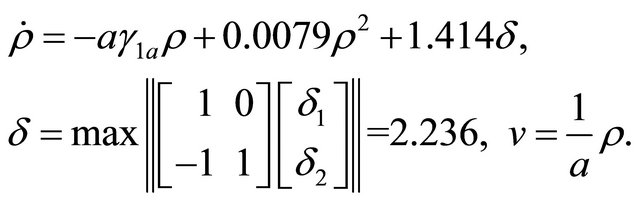 (1.45)
(1.45)
In Figure 5 the value of  for
for  is reported. It is significant to note that for
is reported. It is significant to note that for  it turns out to be
it turns out to be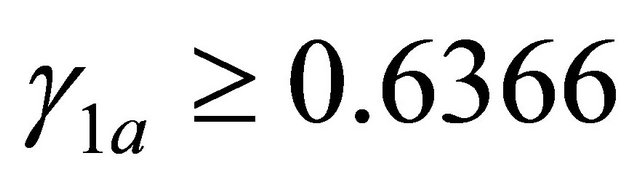 , i.e.
, i.e. 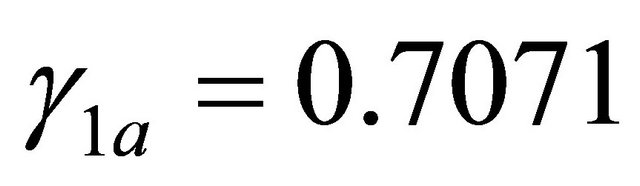 unless 10%, in accord with Theorem 7. For
unless 10%, in accord with Theorem 7. For 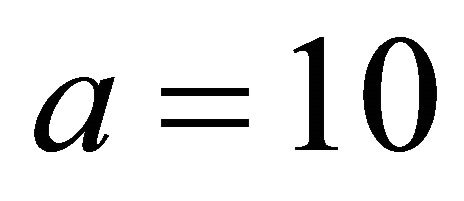 it is
it is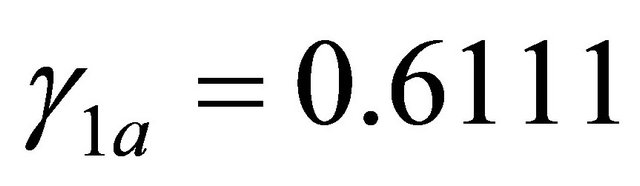 ; hence
; hence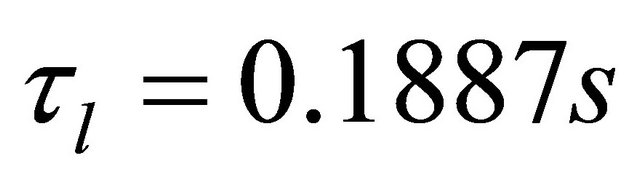 . Moreover it is
. Moreover it is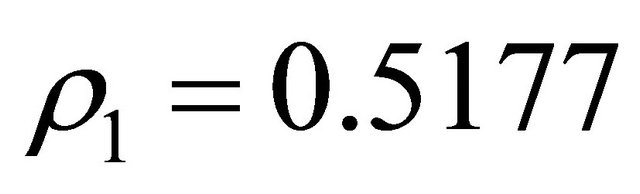 ,
, 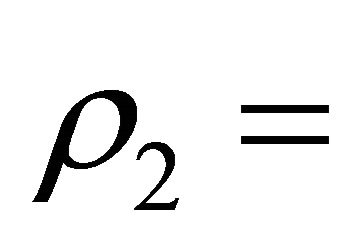 773.0. Therefore, at “steady state”,
773.0. Therefore, at “steady state”, 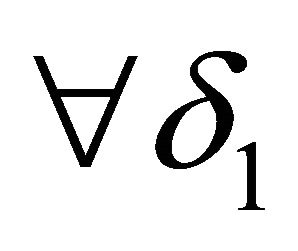 ,
, 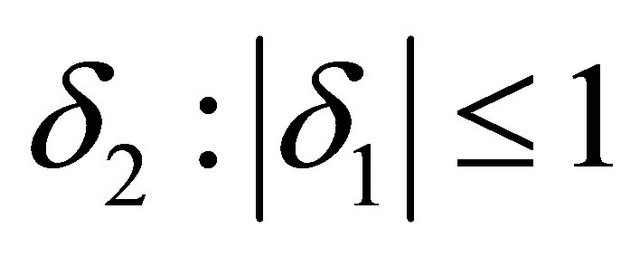 ,
, 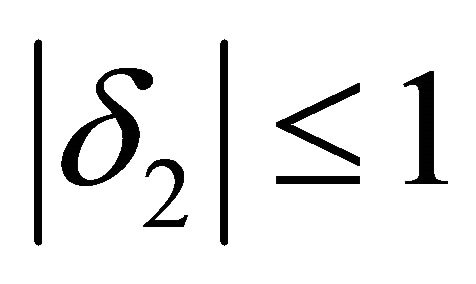 , it is:
, it is:
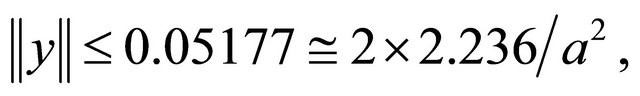

Figure 6 shows the values of 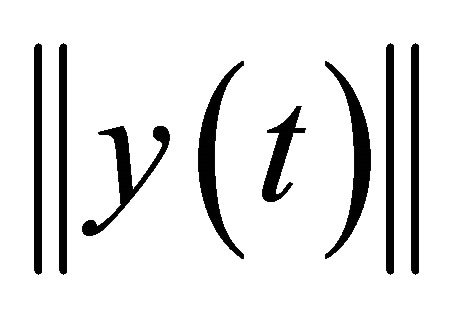 and of
and of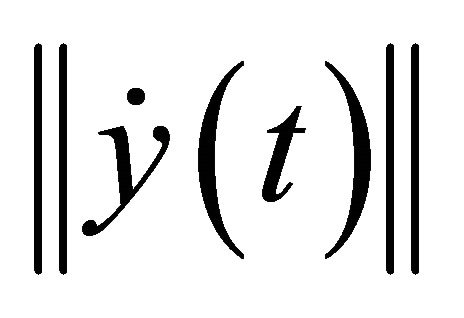 , obtained for
, obtained for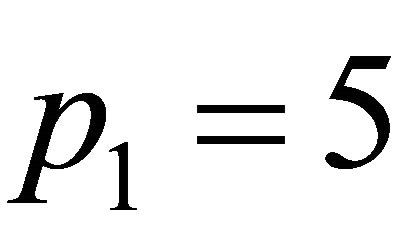 ,
, 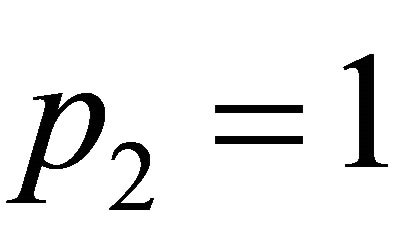 ,
, 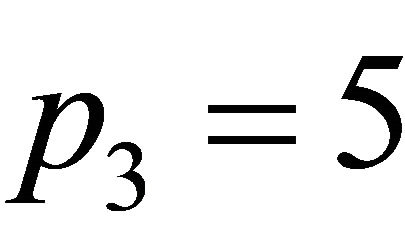 ,
, 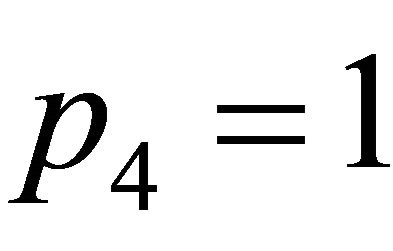 ,
, 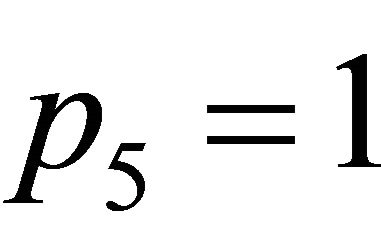 ,
, 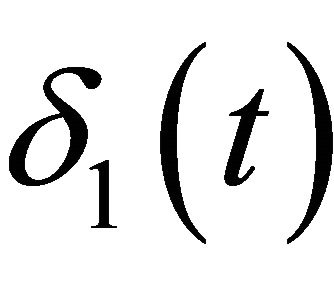 and
and 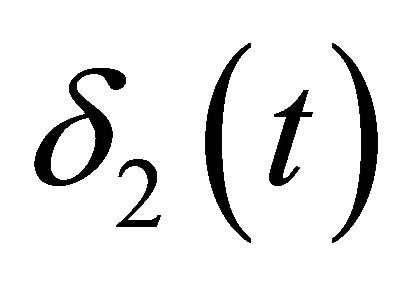 square waves of amplitude 1 and frequency 1.2 Hz,
square waves of amplitude 1 and frequency 1.2 Hz, 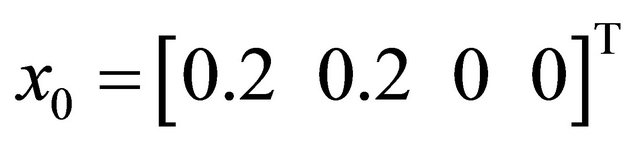 ,
,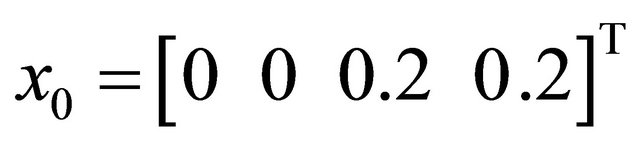 .
.
This figure highlights that the proposed stabilization method is little conservative, as it can be easily verified by simulating the stabilized system for several initial conditions and numerous values of the parameters.
5. Conclusions
In this paper the problem of analysis and practical

Figure 4. Vehicles to be kept still at a distance ds.
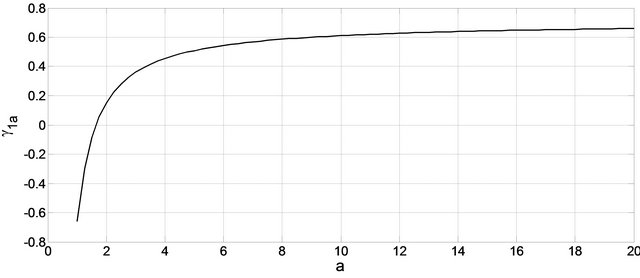
Figure 5. γ1a as a function of a.

Figure 6. Possible time histories of 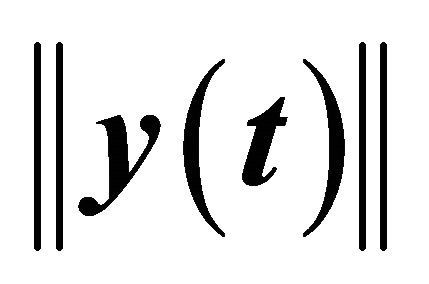 and of
and of .
.
stabilization of a significant class of MIMO nonlinear systems subject to parametric uncertainties, including linear and quadratic ones with an additional bounded nonlinearities and/or disturbances, has been approached. By using the concept of majorant system and via Lyapunov approach, new useful results, explicit formulas and efficient algorithms for designing state feedback control laws, with a possible imperfect compensation of nonlinearities and disturbances, have been stated. These results have been proved that guarantee a specified convergence velocity of the linearized of the majorant system and a desired steady-state output for generic uncertainties and/or nonlinearities and/or bounded disturbances.
The utility and the efficiency of the these results have been shown with two illustrative example.
The presented results can be used to establish further new useful theorems for the tracking of trajectories for relevant MIMO systems, like e.g. the robots.
In this direction the research of the author is going on.
REFERENCES
- G. Ambrosino, G. Celentano and F. Garofalo, “Tracking Control of High-Performance Robots via Stabilizing Controllers for Uncertain Systems,” Journal of Optimization Theory and Applications, Vol. 50, No. 2, 1986, pp. 239- 255. doi:10.1007/BF00939271
- H. Nijmeijer and A. J. Van der Schaft, “Nonlinear Dynamical Control Systems,” Springer-Verlag, Berlin, 1990. doi:10.1007/978-1-4757-2101-0
- J. J. E. Slotine and W. Li, “Applied Nonlinear Control,” Prentice-Hall, Upper Saddle River, 1991.
- B. Brogliato and A. T. Neto, “Practical Stabilization of a Class of Nonlinear Systems with Partially Known Uncertainties,” Automatica, Vol. 31, No. 1, 1995, 145-150. doi:10.1016/0005-1098(94)E0050-R
- R. A. Freeman and P. V. Kokotovic, “Robust Nonlinear Control Design,” Birkhauser, Boston, 1996. doi:10.1007/978-0-8176-4759-9
- A. Isidori, “Nonlinear Control Systems II,” SpringerVerlag, New York, 1999. doi:10.1007/978-1-4471-0549-7
- S. Sastry, “Nonlinear Systems, Analysis, Stability and Control,” Springer-Verlag, New York, 1999.
- X.-Y. Lu and S. K. Spurgeon, “Output Feedback Stabilization of MIMO Non-Linear Systems via Dynamic Sliding Mode,” International Journal of Robust and Nonlinear Control, Vol. 9, No. 5, 1999, pp. 275-305. doi:10.1002/(SICI)1099-1239(19990430)9:5<275::AID-RNC404>3.0.CO;2-F
- L. Moreau and D. Aeyels, “Practical Stability and Stabilization,” IEEE Transactions on Automatic Control, Vol. 45, No. 8, 2000, pp. 1554-1558. doi:10.1109/9.871771
- I. Karafyllis and J. Tsinias, “Global Stabilization and Asymptotic Tracking for a Class of Nonlinear Systems by Means of Time-Varying Feedback,” International Journal of Robust and Nonlinear Control, Vol. 13, No. 6, 2003, pp. 559-588. doi:10.1002/rnc.738
- L. Celentano, “A General and Efficient Robust Control Method for Uncertain Nonlinear Mechanical Systems,” Proceedings of the IEEE Conference on Decision and Control, Seville, 12-15 December 2005, pp. 659-665. doi:10.1109/CDC.2005.1582231
- L. K. Murray and S. Jayasuriya, “An Improved NonSequential Multi-Input Multi-Output Quantitative Feedback Theory Design Methodology,” International Journal of Robust and Nonlinear Control, Vol. 16, No. 8, 2006, pp. 379-395. doi:10.1002/rnc.1061
- E. Moulay and W. Perruquetti, “Finite Time Stability and Stabilization of a Class of Continuous Systems,” Journal of Mathematical Analysis and Applications, Vol. 323, No. 2, 2006, pp. 1430-1443. doi:10.1016/j.jmaa.2005.11.046
- D. V. Efimov and A. L. Fradkov, “Input-to-Output Stabilization of Nonlinear Systems via Backstepping,” International Journal of Robust and Nonlinear Control, Vol. 19, No. 6, 2009, pp. 613-633. doi:10.1002/rnc.1336
- M. L. Corradini, A. Cristofaro and G. Orlando, “Robust Stabilization of Multi-Input Plants with Saturating Actuators,” IEEE Transactions on Automatic Control, Vol. 55, No. 2, 2010, pp. 419-425. doi:10.1109/TAC.2009.2036308
- S. F. Yang, “Efficient Algorithm for Computing QFT Bounds,” International Journal of Control, Vol. 83, No. 4, 2010, pp. 716-723. doi:10.1080/00207170903390161
- F. Amato, C. Cosentino and A. Merola, “Sufficient Conditions for Finite-Time Stability and Stabilization of Nonlinear Quadratic Systems,” IEEE Transactions on Automatic Control, Vol. 55, No. 2, 2010, pp. 430-434. doi:10.1109/TAC.2009.2036312
- S. Ding, C. Qian and S. Li, “Global Stabilization of a Class of Feedforward Systems with Lower-Order Nonlinearities,” IEEE Transactions on Automatic Control, Vol. 55, No. 3, 2010, pp. 691-696. doi:10.1109/TAC.2009.2037455
- L. Celentano, “New Robust Tracking and Stabilization Methods for Significant Classes of Uncertain Linear and Nonlinear Systems,” In: A. Mueller, Ed., Recent Advances in Robust Control—Novel Approaches and Design Methods, InTech, Winchester, 2011, pp. 247-270.
- L. Celentano, “Robust Tracking Controllers Design with Generic References for Continuous and Discrete Uncertain Linear SISO Systems,” LAP—Lambert Academic Publishing, Saarbrücken, 2012.
- L. Celentano, “Robust Tracking Method for Uncertain MIMO Systems of Realistic Trajectories,” Journal of the Franklin Institute, Vol. 350, No. 3, 2013, pp. 437-451. doi:10.1016/j.jfranklin.2012.12.002

