Open Journal of Applied Sciences
Vol.05 No.06(2015), Article ID:57171,10 pages
10.4236/ojapps.2015.56027
Quantum-Inspired Neural Network with Sequence Input
Ziyang Li1*, Panchi Li2
1School of Earth Science, Northeast Petroleum University, Daqing, China
2School of Computer and Information Technology, Northeast Petroleum University, Daqing, China
Email: *liziyangemail@126.com, lipanchi@vip.sina.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 May 2015; accepted 13 June 2015; published 16 June 2015
ABSTRACT
To enhance the approximation and generalization ability of artificial neural network (ANN) by employing the principles of quantum rotation gate and controlled-not gate, a quantum-inspired neuron with sequence input is proposed. In the proposed model, the discrete sequence input is represented by the qubits, which, as the control qubits of the controlled-not gate after being rotated by the quantum rotation gates, control the target qubit for reverse. The model output is described by the probability amplitude of state  in the target qubit. Then a quantum-inspired neural network with sequence input (QNNSI) is designed by employing the sequence input-based quantum-inspired neurons to the hidden layer and the classical neurons to the output layer, and a learning algorithm is derived by employing the Levenberg-Marquardt algorithm. Simulation results of benchmark problem show that, under a certain condition, the QNNSI is obviously superior to the ANN.
in the target qubit. Then a quantum-inspired neural network with sequence input (QNNSI) is designed by employing the sequence input-based quantum-inspired neurons to the hidden layer and the classical neurons to the output layer, and a learning algorithm is derived by employing the Levenberg-Marquardt algorithm. Simulation results of benchmark problem show that, under a certain condition, the QNNSI is obviously superior to the ANN.
Keywords:
Quantum Rotation Gate, Multi-Qubits Controller-Not Gate, Quantum-Inspired Neuron, Quantum-Inspired Neural Network

1. Introduction
Many neuro-physiological experiments indicate that the information processing character of the biological nerve system mainly includes the following eight aspects: the spatial aggregation, the multi-factor aggregation, the temporal cumulative effect, the activation threshold characteristic, self-adaptability, exciting and restraining characteristics, delay characteristics, conduction and output characteristics [1] . From the definition of the M-P neuron model, classical ANN preferably simulates voluminous biological neurons’ characteristics such as the spatial weight aggregation, self-adaptability, conduction and output, but it does not fully incorporate temporal cumulative effect because the outputs of ANN depend only on the inputs at the moment regardless of the prior moment. In the process of practical information processing, the memory and output of the biological neuron not only depend on the spatial aggregation of input information, but also are related to the temporal cumulative effect. Although the ANN in Refs. [2] -[5] can process temporal sequences and simulate delay characteristics of biological neurons, in these models, the temporal cumulative effect has not been fully reflected. Traditional ANN can only simulate point-to-point mapping between the input space and output space. A single sample can be described as a vector in the input space and output space. However, the temporal cumulative effect denotes that multiple points in the input space are mapped to a point in the output space. A single input sample can be described as a matrix in the input space, and a single output sample is still described as a vector in the output space. In this case, we claim that the network has a sequence input.
Since Kak firstly proposed the concept of quantum-inspired neural computation [6] in 1995, quantum neural network (QNN) has attracted great attention by the international scholars during the past decade, and a large number of novel techniques have been studied for quantum computation and neural network. For example, Ref. [7] proposed the model of quantum neural network with multilevel hidden neurons based on the superposition of quantum states in the quantum theory. In Ref. [8] , an attempt was made to reconcile the linear reversible structure of quantum evolution with nonlinear irreversible dynamics of neural network. Ref. [9] presented a novel learning model with qubit neuron according to quantum circuit for XOR problem and described the influence to learning by reducing the number of neurons. In Ref. [10] , a new mathematical model of quantum neural network was defined, building on Deutsch’s model of quantum computational network, which provides an approach for building scalable parallel computers. Ref. [11] proposed the neural network with the quantum gated nodes, and indicated that such quantum network may contain more advantageous features from the biological systems than the regular electronic devices. Ref. [12] proposed a neural network model with quantum gated nodes and a smart algorithm for it, which shows superior performance in comparison with a standard error back propagation network. Ref. [13] proposed a weightless model based on quantum circuit. It is not only quantum-inspired but also actually a quantum NN. This model is based on Grover’s search algorithm, and it can both perform quantum learning and simulate the classical models. However, from all the above QNN models, like M-P neurons, it also does not fully incorporate temporal cumulative effect because a single input sample is either irrelative to time or relative to a moment instead of a period of time.
In this paper, in order to fully simulate biological neuronal information processing mechanisms and to enhance the approximation and generalization ability of ANN, we proposed a quantum-inspired neural network model with sequence input, called QNNSI. It’s worth pointing out that an important issue is how to define, configure and optimize artificial neural networks. Refs. [14] [15] make deep research into this question. After repeated experiments, we opt to use a three-layer model with a hidden layer, which employs the Levenberg-Mar- quardt algorithm for learning. Under the premise of considering approximation ability and computational efficiency, this option is a relatively ideal. The proposed approach is utilized to the time series prediction for Mackey-Glass, and the experimental results indicate that, under a certain condition, the QNNSI is obviously superior to the common ANN.
2. Qubit and Quantum Gate
2.1. Qubit
In the quantum computers, the “qubit” has been introduced as the counterpart of the “bit” in the conventional computers to describe the states of the circuit of quantum computation. The two quantum physical states labeled as 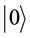 and
and 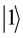 express 1 bit information, in which
express 1 bit information, in which 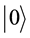 corresponds to the bit 0 of classical computers, while
corresponds to the bit 0 of classical computers, while 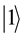 bit 1. Notation of “
bit 1. Notation of “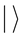 ” is called the Dirac notation, which is the standard notation for the states in the quantum mechanics. The difference between bits and qubits is that a qubit can be in a state other than
” is called the Dirac notation, which is the standard notation for the states in the quantum mechanics. The difference between bits and qubits is that a qubit can be in a state other than 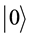 and
and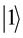 . It is also possible to form the linear combinations of the states, namely superpositions:
. It is also possible to form the linear combinations of the states, namely superpositions:
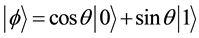 (1)
(1)
An n qubits system has 2n computational basis states. For example, a 2 qubit system has basis ,
, 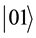 ,
, 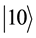 ,
,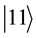 . Similar to the case of a single qubit, the n qubits system may form the superposition of 2n.
. Similar to the case of a single qubit, the n qubits system may form the superposition of 2n.
 (2)
(2)
where  is called probability amplitude of the basis states
is called probability amplitude of the basis states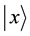 , and
, and 

2.2. Quantum Rotation Gate
In quantum computation, the logic function can be realized by applying a series of unitary transform to the qubit states, which the effect of the unitary transform is equal to that of the logic gate. Therefore, the quantum services with the logic transformations in a certain interval are called the quantum gates, which are the basis of performing quantum computation.
The definition of a single qubit rotation gate is written as

2.3. Quantum NOT Gate
The NOT gate is defined by its truth table, in which 







The notation X for the quantum NOT is used for historical reasons. If the quantum state 



2.4. Multi-Qubits Controlled-Not Gate
In a true quantum system, a single qubit state is often affected by a joint control of multi-qubits. A multi-qubits controlled-not gate 

In Figure 1(a), suppose we have n + 1 qubits, and then we define the controlled operation 


Figure 1. Multi-qubits controlled-not gate. (a) Type 1 control; (b) Type 0 control.
Suppose that the 



It is observed from Equation (7) that the output of 



In Figure 1(b), the operator X is applied to last a qubit if the first n qubits are all equal to zero, and otherwise, nothing is done. The controlled operation 

The probability of the target qubit state


At this time, after the joint control of the n input bits, the target bit 

3. QNNSI Model
3.1. Quantum-Inspired Neuron Model
In this section, we first propose a quantum-inspired neuron model with sequence input, as shown in Figure 2. This model consists of quantum rotation gates and multi-qubits controlled-not gate. The 


Let



where


Figure 2. The model of quantum-inspired neuron with sequence input. (a) Type 1 control; (b) Type 0 control.
for Figure 2(b),
3.2. Quantum-Inspired Neural Network Model
In this paper, the QNNSI model is shown in Figure 3, where the hidden layer consists of quantum-inspired neurons with sequence input, and the output layer consists of classical neurons. The 



Unlike ANN, each input sample of QNNSI is described as a matrix instead of a vector. For example, the l-th sample can be written as

Let

output relationship of quantum-inspired neuron, in interval

The j-th output in hidden layer (namely, the spatial and temporal aggregation results in [0, T]) is given by

The k-th output in output layer can be written as

4. QNNSI Algorithm
4.1. Pretreatment of Input and Output Samples
Suppose the l-th sample in n-dimensional input space


Figure 3. The model of quantum-inspired neural network with sequence input.

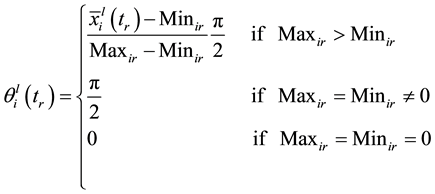
These samples can be converted into the quantum states as follows

where
Similarly, suppose the 



then, these output samples can be normalized by the following equation

4.2. QNNSI Parameters Adjustment
In QNNSI, the adjustable parameters include the rotation angles of quantum rotation gates in hidden layer, and the weights in output layer. Suppose 


Let

According to the gradient descent algorithm in Ref. [16] , the gradient of the rotation angles of the quantum rotation gates can be calculated as follows

where
The gradient of the connection weights in output layer can be calculated as follows

Because gradient calculation is more complicated, the standard gradient descent algorithm is not easy to converge. Hence we employ the Levenberg-Marquardt algorithm in Ref. [16] to adjust the QNNSI parameters.
Let P denote the parameter vector, e denote the error vector, and J denote the Jacobian matrix. p, e, and J are respectively defined as follows



According to Levenberg-Marquardt algorithm, the QNNSI iterative equation is written as follows

where 



4.3. Stopping Criterion of QNNSI
If the value of the evaluation function E reaches the predefined precision within the preset maximum of iterative steps, then the execution of the algorithm is stopped, else the algorithm is not stopped until it reaches the predefined maximum of iterative steps.
5. Simulations
To examine the effectiveness of the proposed QNNSI, the time series prediction for Mackey-Glass is used to compare it with the ANN with a hidden layer in this section. In this experiment, we implement and investigate the QNNSI in Matlab (Version
Mackey-Glass time series can be generated by the following iterative equation [17]

where 





From the above equation, we may obtain the time sequence
set, and the remaining 200 as the testing set. Our prediction schemes is to employ n data adjacent to each other to predict the next one data. Namely, in our model, the sequence length equals to n. Therefore, each sample consists of n input values and an output value.
Hence, there is only one output node in QNNSI and ANN. In order to fully compare the approximation ability of two models, the number of hidden nodes are respectively set to

Obviously, ANN has n input nodes, and an ANN’s input sample can be described as a n-dimensional vector. For the number of input nodes of QNNSI, we employ the following nine kinds of settings shown in Table 1. For each of these settings in Table 1, a single QNNSI input sample can be described as a matrix.
It is worth noting that, in QNNSI, an 





Our experiment scheme is that, for each kind of combination of input nodes and hidden nodes, one ANN and nine QNNSIs are respectively run 10 times. Then we use four indicators, such as average approximation error, average iterative steps, average running time, and convergence ratio, to compare QNNSI with ANN. Training result contrasts are shown in Tables 2-5, where QNNSIn_q denotes QNNSI with n input nodes and q sequence length.
From Tables 2-5, we can see that when the input nodes take 6, 9, and 12, the performance of QNNSIs are
Table 1. The input nodes and the sequence length setting of QNNSIs and ANN.
Table 2. Training result contracts of average approximation error.
Table 3. Training result contracts of average iterative steps.
Table 4. Training result contracts of average running time (s).
Table 5. Training result contracts of convergence ratio (%).
obviously superior to that of ANN, and the QNNSIs have better stability than ANN when the number of hidden nodes changes.
Next, we investigate the generalization ability of QNNSI. Based on the above experimental results, we only investigate three QNNSIs (QNNSI6_6, QNNSI9_4, and QNNSI12_3). Our experiment scheme is that three QNNSIs and one ANN train 10 times on the training set, and the generalization ability is immediately investigated on the testing set after each training. The average results of the 10 tests are regarded as the evaluation indexes. For convenience of description, let 


Taking 30 hidden nodes for example, the evaluation indexes contrast of QNNSIs and ANN are shown in Table 6. The experimental results show that the generalization ability of three QNNSIs is obviously superior to that of corresponding ANN.
These experimental results can be explained as follows. For processing of input information, QNNSI and ANN take different approaches. QNNSI directly receives a discrete input sequence. In QNNSI, using quantum information processing mechanism, the input is circularly mapped to the output of quantum controlled-not gates in hidden layer. As the controlled-not gate’s output is in the entangled state of multi-qubits, therefore, this mapping is highly nonlinear, which make QNNSI have the stronger approximation ability. In addition, QNNSI’s each input sample can be described as a matrix with n rows and q columns. It is clear from QNNSI’s algorithm that, for the different combination of n and q, the output of quantum-inspired neuron in hidden layer is also different. In fact, The number of discrete points q denotes the depth of pattern memory, and the number of input nodes n denotes the breadth of pattern memory. When the depth and the breadth are appropriately matched, the QNNSI shows excellent performance. For the ANN, because its input can only be described as a nq-dimensional vector, it is not directly deal with a discrete input sequence. Namely, it only can obtain the sample characteristics by way of breadth instead of depth. Hence, in the ANN information processing, there exists inevitably the loss of sample characteristics, which affects its approximation and generalization ability.
It is worth pointing out that QNNSI is potentially much more computationally efficient than all the models referenced above in the Introduction section. The efficiency of many quantum algorithms comes directly from quantum parallelism that is a fundamental feature of many quantum algorithms. Heuristically, and at the risk of over-simplifying, quantum parallelism allows quantum computers to evaluate a function f(x) for many different values of x simultaneously. Although quantum simulation requires many resources in general, quantum parallelism leads to very high computational efficiency by using the superposition of quantum states. In QNNSI, the input samples have been converted into corresponding quantum superposition states after preprocessing. Hence, as far as a lot of quantum rotation gates and controlled-not gates used in QNNSI are concerned, information processing can be performed simultaneously, which greatly improves the computational efficiency. Because the above experiments are performed in classical computer, the quantum parallelism has not been explored. However, the efficient computational ability of QNNSI is bound to stand out in future quantum computer.
6. Conclusion
This paper proposes quantum-inspired neural network model with sequence input based on the principle of quantum computing. The architecture of the proposed model includes three layers, where the hidden layer consists of quantum-inspired neurons and the output layer consists of classical neurons. An obvious difference from classical ANN is that each dimension of a single input sample consists of a discrete sequence rather than a single value. The activation function of hidden layer is redesigned according to the principle of quantum computing. The Levenberg-Marquardt algorithm is employed for learning. With application of the information processing mechanism of quantum rotation gates and controlled-not gates, the proposed model can effectively obtain the sample
Table 6. The average prediction error contrasts of QNNSIs and ANN.
characteristics by ways of breadth and depth. The experimental results reveal that a greater difference between input nodes and sequence length leads to a lower performance of proposed model than that of classical ANN; on the contrary, it obviously enhances approximation and generalization ability of proposed model when input nodes are closer to sequence length. The following issues of the proposed model, such as continuity, computational complexity, and improvement of learning algorithm, are subjects of further research.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61170132), Natural Science Foundation of Heilongjiang Province of China (Grant No. F2015021), Science Technology Research Project of Heilongjiang Educational Committee of China (Grant No. 12541059), and Youth Foundation of Northeast Petroleum University (Grant No. 2013NQ119).
References
- Tsoi, A.C. and Back, A.D. (1994) Locally Recurrent Globally Feed Forward Network: A Critical Review of Architectures. IEEE Transactions on Neural Network, 7, 229-239. http://dx.doi.org/10.1109/72.279187
- Kleinfeld, A.D. (1986) Sequential State Generation by Model Neural Network. Proceedings of the National Academy of Sciences USA, 83, 9469-9473. http://dx.doi.org/10.1073/pnas.83.24.9469
- Waibel, A., Hanazawa, A. and Hinton, A. (1989) Phoneme Recognition Using Time-Delay Neural Network. IEEE Transactions on Acoustics, Speech, and Signal Processing, 37, 328-339. http://dx.doi.org/10.1109/29.21701
- Lippmann, R.P. (1989) Review of Neural Network for Speech Recognition. Neural Computation, 1, 1-38. http://dx.doi.org/10.1162/neco.1989.1.1.1
- Maria, M., Marios, A. and Chris, C. (2011) Artificial Neural Network for Earthquake Prediction Using Time Series Magnitude Data or Seismic Electric Signals. Expert Systems with Applications, 38, 15032-15039. http://dx.doi.org/10.1016/j.eswa.2011.05.043
- Kak, S. (1995) On Quantum Neural Computing. Information Sciences, 83, 143-160. http://dx.doi.org/10.1016/0020-0255(94)00095-S
- Gopathy, P. and Nicolaos, B.K. (1997) Quantum Neural Network (QNN's): Inherently Fuzzy Feed forward Neural Network. IEEE Transactions on Neural Network, 8, 679-693. http://dx.doi.org/10.1109/72.572106
- Zak, M. and Williams, C.P. (1998) Quantum Neural Nets. International Journal of Theoretical Physics, 3, 651-684. http://dx.doi.org/10.1023/A:1026656110699
- Maeda, M., Suenaga, M. and Miyajima, H. (2007) Qubit Neuron According to Quantum Circuit for XOR Problem. Applied Mathematics and Computation, 185, 1015-1025. http://dx.doi.org/10.1016/j.amc.2006.07.046
- Gupta, S. and Zia, R.K. (2001) Quantum Neural Network. Journal of Computer and System Sciences, 63, 355-383. http://dx.doi.org/10.1006/jcss.2001.1769
- Shafee, F. (2007) Neural Network with Quantum Gated Nodes. Engineering Applications of Artificial Intelligence, 20, 429-437. http://dx.doi.org/10.1016/j.engappai.2006.09.004
- Li, P.C., Song, K.P. and Yang, E.L. (2010) Model and Algorithm of Neural Network with Quantum Gated Nodes. Neural Network World, 11, 189-206.
- Adenilton, J., Wilson, R. and Teresa, B. (2012) Classical and Superposed Learning for Quantum Weightless Neural Network. Neurocomputing, 75, 52-60. http://dx.doi.org/10.1016/j.neucom.2011.03.055
- Israel, G.C., Angel, G.C. and Belen, R.M. (2012) Dealing with Limited Data in Ballistic Impact Scenarios: An Empirical Comparison of Different Neural Network Approaches. Applied Intelligence, 35, 89-109.
- Israel, G.C., Angel, G.C. and Belen, R.M. (2013) An Optimization Methodology for Machine Learning Strategies and Regression Problems in Ballistic Impact Scenarios. Applied Intelligence, 36, 424-441.
- Martin, T.H., Howard, B.D. and Mark, H.B. (1996) Neural Network Design. PWS Publishing Company, Boston, 391- 399.
- Mackey, M.C. and Glass, L. (1977) Oscillation and Chaos in Physiological Control System. Science, 197, 287-289. http://dx.doi.org/10.1126/science.267326
NOTES
*Corresponding author.






