Received 4 June 2015; accepted 25 July 2015; published 28 July 2015

ABSTRACT

In the general theory of relativity, the fundamental metric tensor plays a special role, which has its physical basis in the peculiar aspects of gravitation. The fundamental property of gravitational fields provides the possibility of establishing an analogy between the motion in a gravitational field and the motion in any external field considered as a noninertial system of reference. Thus, the properties of the motion in a noninertial frame are the same as those in an inertial system in the presence of a gravitational field. In other words, a noninertial frame of reference is equivalent to a certain gravitational field. This is known as the principle of equivalence. From the mathematical viewpoint, the same special role can be played by the small deformation strain tensor, which describes the geometrical properties of any region deformed because of the effect of some external agent. It can be proved that, from that tensor, all the mathematical structures needed in the general theory of relativity can be constructed.

Keywords:

The Small Deformation Strain Tensor, The Fundamental Metric Tensor

1. Introduction

Within the theoretical frame of classical fluid dynamics, the effect of applied forces to any continuous medium is studied. Under the action of applied forces, the region occupied by the continuous medium exhibits deformations to some extent, that is to say, the region changes in shape and volume. Those deformations can be described mathematically by the small deformation strain tensor. When the deformation is the result of a process of hydrostatic or volumetric compression or expansion, the small deformation strain tensor is reduced to the sum of the elements of its principal diagonal, that is, its trace. This trace is likewise in this case, the fractional change of the volume element of the region occupied by the continuous medium. Thus, when the deformations are small, the trace of the small deformation strain tensor is nearly equal to the reciprocal of the mass density. Then, that characteristic property of the matter is contained in that tensor [1] .

2. The Small Deformation Strain Tensor and the Fundamental Metric Tensor

Consider an ordered set of N real variables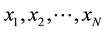. These variables are called the coordinates of a point. Thus, all the points corresponding to all values of the coordinates are said to form an N-dimensional space. Let R be any region in that space, and let us consider two points very close together. If over the boundary surface of R an external force is applied, the geometry of the region changes inform and size; that is to say, it is deformed. In order to mathematically describe the deformation, the procedure is as follows. Be dx_i the i-component of the radius vector joining the points before the deformation, and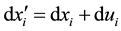, the radius vector joining them in the deformed region; where 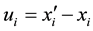is the i-component of the displacement vector; which is only a function of the coordinates x_i [1] . The distances between the points before and after deformation respectively are

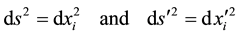(1)

so that,

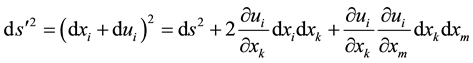; (2)

where the following expansion was used

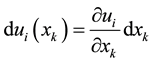. (3)

Since the summation is taken over both suffixes i and k, the second term on the right of (2) can be written as

.

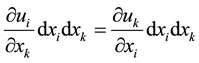In the third term on the right of (2), the surffixes i and m can be interchanged, in order to finally obtain that

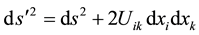; (4)

where

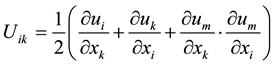, (5)

are the components of the strain tensor. From its definition, it is clear that it is a symmetrical tensor, that is to say

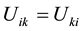. (6)

For small deformations it is possible to neglect the last term in (2) and write that

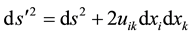; (7)

where

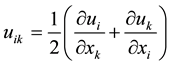, (8)

are the components of the small deformation strain tensor [1] . On the other hand, after deformation the distance between the near by points, can be written as follows

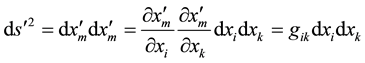; (9)

where

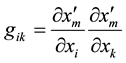, (10)

are the components of the fundamental metric tensor, and the summation convention was used. Since further, 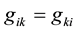is a simmetrical covariant tensor of the second rank [2] .

Now, if instead considering that the points are separate we make them coincide in the undeformed initial situation, it is clear that

.

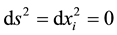In that case, in (7) it is obtainedw that

. (11)

If Equations (9) and (11) are compared we have that

, (12)

that is to say,

. (13)

Equation (12) must be considered as a relation of congruence between physics and geometry more than equality. Since further is a simmetrical covariant tensor of the second rank, also; and it can be considered that it is equivalent to the fundamental metric tensor, apart from the unessential factor 1/2. That means that both tensors have the same properties [3] .

Now, if in the determinant formed by the elements u_ik, and taking into account the co-factor of each of the u_ik and divide by the determinant u, certain quantities are obtained, as we shall demonstrate soon, form a contravariant tensor. In fact, by a well known property of determinants, it can be obtained that

; (14)

where

On the other hand, if instead of the expression for we may thus write, or by (14), it can be see that, according to the multiplication tensor rules

form a covariant four-vector. In that case,

.

Since this, with the arbitrary choice of the vector dh_n, ds² is a scalar, and u^nr by its definition is symmetrical, it follows that u^nr is a contravariant tensor. It further follows from (14) that is also a tensor, which we will call the miked fundamental tensor [4] . Now, by the rule for the multiplication of determinants

.

On the other hand

;

in such a way that

.

Besides, from Equation (12) it is obtained that

.

Now, and given that,

.

Finally, if

,

it is fulfilled that

.

In that case,

.

In the general theory of relativity, it is used to write inestead of, with g the determinant of g_ik, quantity which is always real; because of the hyperbolic character of the space-time continuum [3] . Due to the same past arguments, it is possible to propose the use of instead of. This is so, because really, for all coordinates connected with a real space-time, the determinant g, and also, the determinant u, are negative [5] .

3. The Christoffel Symbols

A curve in space is defined as the locus of a point whose coordinates depend on a single parameter [2] . Consider a given curve and let us suppose that the coordinates of any point on it, are functions of the parameter t. If we take any vector at a given point of the curve and at every other point on it, take the vector equal to it in magnitude and parallel to it in direction, we obtain a vector C defined at each point of the curve, and the components of X, will be functions of t. In other words, we have a parallel field of vectors along the given curve [2] . Our objective is to find the differential equations which such a vector-field must satisfy. In order to do so, it is necessary to consider Cartesian coordinates y^r. Let Y^r be the components of the vector-field in this coordinate system [2] . Since the components of parallel vectors are equal in Cartesian Systems, it is easy to see that the Y^r are all constants along the curve and consequently the derivatives of Y^r with respect to t are zero [2] . Now, it is clear that

. (15)

Therefore, differentiating with respect to t we have that dYⁱ/dt = 0, and then, it is fulfilled that

. (16)

Now, let us consider the following transformation

.

If we multiply Equations (16) by the last transformation, the relationships (8) and (10) are used, and sum i from 1 to 3, it is obtained that [2] .

; (17)

where the relationship (8) was used, and clearly, the factor 1/2 was sup-pressed.

Next, let us consider the expression

;

and referring again the relationship (8), we get, on differentiating partially with respect to x^r that

. (18)

These equations are true when m, n, p take any of the values 1, 2, 3. If now we take any of the two equations obtained by permuting m, n, p cyclically in (18), and substract (18) from their sum, we obtain

. (19)

Hence if we write by brevity

(20)

and substitute this in (19), it is obtained the following result

.

If on the other hand, we write

(21)

it is obtained Equation (16) in the final form

, (22)

and the parallel vector-field along the given curve must satisfy this differential equation [2] .

The quantitites [m n, p] and {m n, r}, defined by (20) and (21), in terms of the components of the small deformation tensor, we will call the Christoffel symbols of the first and second kinds, or they are sometimes referred as the three-index symbols [2] [4] . It is seen at once that they are symmetrical in m, n; an important property [2] .

4. Equations of a Geodesic

In order to obtain the equations of a geodesic or path between two points in the Riemannian space, we will use the calculus of variations, and the following condition [4] ,

.

This absolute track is of fundamental importance in dynamics. Keeping the beginning and the end o the path fixed, we give every intermediate point an arbitrary infinitesimal displacement δx_σ so as to deform the path. According to definition (11), it has that

(23)

The stationary condition is

; (24)

in such a way that in (23) we get

;

where we will use greek index instead of latin index, and for convenience, a factor 1/2 has been eliminated

Changing dummy suffixes in the last two terms, it is obtained that

.

Consider the terms enclosed in the round parenthesis. Applying the method of partial integration, we get

.

The first term is an exact differential. It is zero because the δx_σ varishes at both limits of the integral. Hence, it is obtained that

.

This must hold for all values of the arbitrary displacements δx_σ at all points, hence the coefficient in the integrand must vanish at all points on the path [4] . Thus

now, it is clear that [4]

and

.

Also, in the last two terms we replace the dummy suffixes μ and υ by ε.

The equation then becomes

. (25)

We can get rid of the factor u_εσ by multiplying through by u^σα in such a way that

. (26)

However,

,

is one of Christoffel’s 3-index symbols. Finally, in (26) we obtain that

. (27)

This is the looked for differential equation. For α = 1, 2, 3, 4 that relationship gives the four equations determining a geodesic [4] .

5. Covariant Derivative of a Vector

Since dx_μ is a contravariant vector, and ds an invariant, dx_μ/ds a kind of velocity, is a contravariant vector. Hence if A_μ is any covariant vector, the inner product

.

The rate of change of this expression per unit interval ds along any assigned curve must also be independent of the coordinate system; that is to say

. (28)

This assumes that we keep to the same absolute curve however the coordinate system is varied. The result (28) is therefore only of practical use if it is applied to a curve which is defined independently of the coordinate system; and then, we shall apply it to a geodesic. Performing the differentiation, we get that

, (29)

is invariant along a geodesic.

Now, if Equation (27) is used, we have that along a geodesic

.

With this result in (29) we get that

.

The result is now general since the curvature, which distinguishes the geodesic, has been eliminated by using Equations (27), and only the gradient of the curve, dx_μ/ds and dx_υ/ds, has been left in the expression.

Since dx_μ/ds and dx_υ/ds are contravariant vectors, their co-factor is a covariant tensor of second rank. We therefor write

; (30)

and the tensor A_μυ is called the covariant derivative of A_μ. By raising a suffix we obtain two associated tensors and which must be distinguished since the two suffixes are not symmetrical. The first of these is the most important, and is to be understood when the tensor is written simply as without distinction of its original position [4] . Since

,

we have by (30)

due to

.

So that

;

because [4]

Hence multiplaying through by u^μυ and given that u^μσu_σε is a substitution-operator, we have

. (31)

This is called the covariant derivative of A^μ. The tensors and A^μυ are called the contravariant derivative of A_μ and A^μ.

6. Covariant Derivative of a Tensor

The covariant derivatives of tensors of the second rank are formed as follows [4]

(32)

(33)

. (34)

Thus, the general rule for covariant differentiation with respect to x_σ is ilustrated by the next example [4] .

(35)

The above formula is primarly definitions. We have to prove that the quantities on the right are actually tensors. This is done by a generalization of the method of the preceding section. Thus if in place of (28) we use the following expression

as invariant along a geodesic, we obtain

.

Then substituting for the second derivatives from (27) the expression reduces to

,

showing that A_μυσ is a tensor.

Applying (34) to the fundamental tensor, we have

due to the fact that

. (36)

Hence, the covariant derivatives of the fundamental tensors vanish identically and the fundamental tensors can be treated as constants in covariant differentiation. The utility of the covariant derivative arises from the fact that, when the u_μυ are constants, the Christoffel symbols vanish and the covariant derivative reduces to the ordinary derivative. Now, in general, the physical equations have been stated for the case of Galilean coordinates in which the u_μυ are constants; and we may in Galilean equations replace the ordinary derivative by the covariant derivative without altering anything. This is a necessary step in reducing such equations to the general tensor for which holds true for all coordinates systems [4] .

7. The Riemann-Christoffel Tensor

The second covariant derivative of A_μ is found by inserting in (34) the value of A_μυ given in (30). That is to say

(37)

The first five terms are unaltered when υ and α are interchangel. The last two terms may be written, by changing the dummy suffix α to ε in the last term, in such a way that we get

.

Hence

(38)

The quotient theorem shows that the co-factor of A_ε must be a tensor; so that, it is fulfilled that [4]

; (39)

where

. (40)

This is called the Riemann-Christoffel Tensor. It is only when this tensor vanishes that the order of covariant differentitation is permutable [4] .

The suffix ε may be lowered. Thus

(41)

where ε has been replaced by α in the last two terms. Hence,

(42)

where the relationships (36) and (20) has been used.

It will be seen from (42) that B_μυσρ, beside being antisymmetrical in υ and σ, is also antisymmetrical in μ and ρ. Also it is symmetrical for the double interchange μ and υ, ρ and σ.

It has the further cyclic property [4]

; (43)

as is easily verified from (42). The Riemann-Christoffel tensor has 20 independent components [4] . That tensor is derived solely from the u_{μ < υ}, and also from the g_μυ, and therefore belongs to the class of fundamental tensors [4] .

8. Physical Significance of the Tensor u_μυ

In order to get the physical significance of the fundamental tensor fields u_μυ and g_μυ, let us consider a region of space-time in which the gravitational field vanishes. If we introduce a non-inertial coordinate system, free bodies will be accelerated with respect to the chosen coordinate system, although they move along straight world lines [6] . In other words, the equation of motion of a particle in a gravitational field can be obtained by an appropriate generalization for the free motion of a particle in the special theory of relativity; that is to say, in a Galilean four-dimentional coordinate system. These equations are dw_a/ds = 0, or dw_a = 0; where w_a = dx_a/ds is the four-velocity. Clearly, in curvilinear coordinates we have that

. (44)

Dividing this equation by ds we get

.

This is the required equation of motion. But, this is the same relationship (27) of a geodesic. We see that the motion of a particle in a gravitational field is determined by the quantities {μυ, α}. The derivative is the four-acceleration of the particle. Therefore we may call the quantity

(45)

the four-force, acting on the particle in the gravitational field. Here, the tensor u_μυ plays the role of the potential of the gravitational field; in such a way that, its derivatives determine the field intensity {μυ, α} [5] [6] . It can be shown that by a suitable choice of the coordinate system it is always make all the {μυ, α} zero at an arbitrary point of space-time. We now see that the choice of such a locally-inertial system or locally-geodesic system [5] of reference, means the elimination of the gravitational field in the given infinitesimal element of space-time, and the possibility of making such choice is an expression of the principle of equivalence in the relativistic theory of gravitation [5] .

9. The Law of Gravitation in Empty Space

That law can also be obtained from the fundamental tensors u_μν and B_μνσρ. The later has been expressed in terms of the former, and its first and second derivatives. Thus, the contracted Riemann-Christoffel tensor, denoted by D_μν, is formed setting ε = σ in the relationship (41). That is to say

(46)

The 3-index symbols containing a duplicated suffix can be simplified by means of the expression (A.7). Hence, with some changes of dummy suffixes, it has that

(47)

The expression

, (48)

in empty space, is chosen as the law of gravitation in a Dynamic Theory of Gravitation.

10. Conclusion

Through the present paper, it was possible to demonstrate that the small deformation strain tensor could be used as a fundamental metric tensor, instead of the usual fundamental metric tensor. Also, it was possible to prove that from that tensor, not only other mathematical structures could be constructed, but also another fundamental tensor was obtained; that was to say, we had constructed two of them, u_μυ, and B_μυσρ. It is through these tensors that the gap between pure geometry and physics is bridged. In particular, u_μυ relates the observed interval ds to the mathematical coordinate specification dx_μ. Also, the u_μυ appear as the potentials of the inertial field [6] . Therefore, it is reasonable to assume that, in the presence of a gravitational field, the u_μυ is again the potential which determines the accelerations of free bodies; in other words, the u_μυ is the potential of the gravitational field. Thus, a stage has been reached at which the results obtained can be applied to the theory of gravitation [4] . However, that task that would not be repeated here was established by Albert Einstein, and finally formulated by him in 1916, as probably the most beautiful of the physical theories.

Cite this paper

Angel FierrosPalacios, (2015) The Small Deformation Strain Tensor as a Fundamental Metric Tensor. Journal of High Energy Physics, Gravitation and Cosmology,01,35-47. doi:

References

Appendix

Some Useful Mathematical Expressions

Since

(A.1)

where is the Kronecker delta; such that

it has that

.

Hence

(A.2)

In a similar way,

(A.3)

Now, and multiplying by a contravariant tensor; it has by the rule for lowering suffixes that

(A.4)

For any tensor C_ab other than the fundamental small deformation strain tensor, the corresponding formula would be the following

;

by the expressions

(A.5)

The exception for u_αb arises because a change du_αb has an additional indirect effect through alterning the operation of raising and lowering suffixes.

On the other hand, du is formed taking the differential of each u_µv and multiplying by its co-factor u・u^µv in the determinant. So that

;

in such a way that

. (A.6)

In that case, the contracted 3-index Christoffel symbol becomes

The other two terms cancel each other by interchange of the dummy suffixes σ and l. Hence, by (A. 6) it has that

; (A.7)

this is so, because for real coordinates u is always negative.