Paper Menu >>
Journal Menu >>
 Energy and Power Engineering, 2013, 5, 177-181 doi:10.4236/epe.2013.54B034 Published Online July 2013 (http://www.scirp.org/journal/epe) Forecast of Power Generation for Grid-Connected Photovoltaic System Based on Grey Theory and Verification Model Ying-zi Li1, Jin-cang Niu2, Li Li3 1College of Information and Electrical Engineering, Beijing University of Civil Engineering and Architecture, Beijing, P. R. China 2Beijing Electric Power Corporation, Beijing, P. R. China 3Beijing Huaxing Hengye Electric Equipment Co.Ltd, Beijing, P. R. China Email: yingzi-li@126.com, Niujincang@bj.sgcc.com.cn, lili2082212@sina.com <mailto:lili2082212@sina.com> Received September, 2012 ABSTRACT Being photovoltaic power generation affected by radiation strength, wind speed, clouds cover and environment tem- perature, the generating in each moment is fluctuating . The operational characteristics of grid-connected PV systems are coincided with gray theory application conditions. A gray theory model has been applied in short-term forecast of grid-connected photovoltaic system. The verification model of the probability of small error will help to check the ac- curacy of the gray forecast results. The calculated result shows that th1) model accuracy has been greatly enhanced e . (1,GM Keywords: Forecast of Power Generation; Grid-connected Photovoltaic System ; Data Discretization; Greedy Algo- rithm; Continuous Attributes; Rough Sets 1. Introduction The grid-connected PV power generation has become the trend of the development of solar photovoltaic applica- tions. But its intermittent and randomness will cause the grid scheduling difficulties and bring some adverse ef- fects of the grid. So the forecast of PV power generation will help the grid-connected PV capacity within the con- trol range and minimize the adverse effects, as in [1,2]. The gray system theory is satisfied to th e less data and uncertainty problem. It is consisted of a few basic part, they are gray system analysis, gray model, gray forecast, gray decisions, gray control and gray optimization tech- niques. The gray forecast establishes differential equa- tions using gray numbers that is GM model (gray model) means that the first-order differential equa- tions are composed of N variables. Commonly, used in load forecasting model, the essence is accumulated and generated by the original sequence in order to find some certain laws in generated sequen ces, to fit a typical curve and to establish th e mathematical model, as in [3-5]. (1, )GM N Known the photovoltaic power generation can be re- garded as white elements and unknown generation as black elements. Therefore, a part of the information is clear, the other is unknown, and that is a typical gray system. Daily generation capacity of PV system shows normal distribution. Limited by maximum solar radiation values, the trend of generation is monotonous and graded. So this kind of incomplete information system is just suitable for the object of gray forecast, as in [6,7]. 2. Gray Theory Model With original non- negati ve sa mple sequence (0)(0) (0)(0) (1), (2), () x xx xk, the gray system theory uses a unique the data preproc- essing way , in which one order sequence (0) () x k is accumulated. (1) (0) 1 ()( ),(1) k m x kxmkk n Then it can generate the series. (1)(1) (1)(1) ()(1), (2),, () x kx xxk To establish the first-order linear differential equations about (1) () x k. (1) (1) dx ax u dt Using the least-squares method solves the parameters Copyright © 2013 SciRes. EPE  Y. Z. LI ET AL. 178 ,au. 1 ˆ()( a u TT N ABBB )Y (1) (1) (1) (1) (1) (1) (0) (0) (0) 1((1)(2)) 1 2 1( (2)(3))1 2 1((1) ())1 2 (2) (3) () xx xx xn xn x x xn N B Y where, a is the development parameter for reflecting the development trends of sequence (1) x , u is the coordina- tion parameter for r e f l e c t i ng the change rel a tion of da ta. The gray forecast model about (1,1)GM (1) x is (1) (0) ˆ(1)(1) 0,1,2,, 1 uu ak xk xe aa kn The actual forecast result (0) ˆ x is (0)(1) (1) (0) (0) ˆˆˆ (1)(1) ( ˆ(1) (1) 1, 2,,1 ) x kxkx xx kn k 3. Verification Model The generation forecast is based on the original input data to establish the forecast model, to identify the pa- rameters of the model and to predict. Forecast error range is not only concerned about the forecast results, but also concerned about the forecast results. In the theory of gray forecast, the verification indicators of the model effect are the ratio of posterior error, the probability of small error and the degree of association. (0) () x k, is the original sequence. The gray forecast data sequence is (1kk n)(0) ˆ(),1,2, , x kk n. The process of verification model is shown as follow. Average of th e original sequence is (0) (0) 1 1() n k x xk n Point wise residuals is (0) (0) ˆ () () 1, 2,, kxkxk kn Averag e residuals is 1 1n k k n Average variance of original data is 22 (0) (0) 111 11 () () nn kk s xkx uk nn Average variance of residuals is 2 21 1n k sk n Ratio of posterior error is 2 1 s c s Probability of small error is 1 0.6745pP ks Point wise association coefficient is min max max , 01 () kk Degree of association is 1 1n k k n The gray system error decision analysis is shown in Table 1. The solution of gray forecast model is the exponential curve. The geometry of forecast value is a smooth curve, which is either monotone increasing or monotone decreasing. Although the daily power genera- tion of PV systems trends the exponentially graded, the randomness of model data has been we aken ed in accumulating processing. But influenced by the fore- cast trends of original sequence,the randomness and vo- latility of data sequence fit ineffective. (1,1)GM (1,1)GM Being photovoltaic power generation affected by ra- diation strength, wind speed, clouds cover and environ- ment temperature, the generating in each moment is fluctuating. So only using the gray forecast model is dif- ficult to achieve forecast accuracy. The forecast model based on advanced gray theory is necessary. Table 1. Grade of forcats accuracy. GradeProbability of small error pRatio of posterior error cEvaluate 1 0.95,1.00 0.00,0.35 excellent 2 0.80,0.95 0.35,0.50 good 3 0.70,0.80 0.50,0.65 pass 4 0.00,0.70 0.65,1.00 fail Copyright © 2013 SciRes. EPE 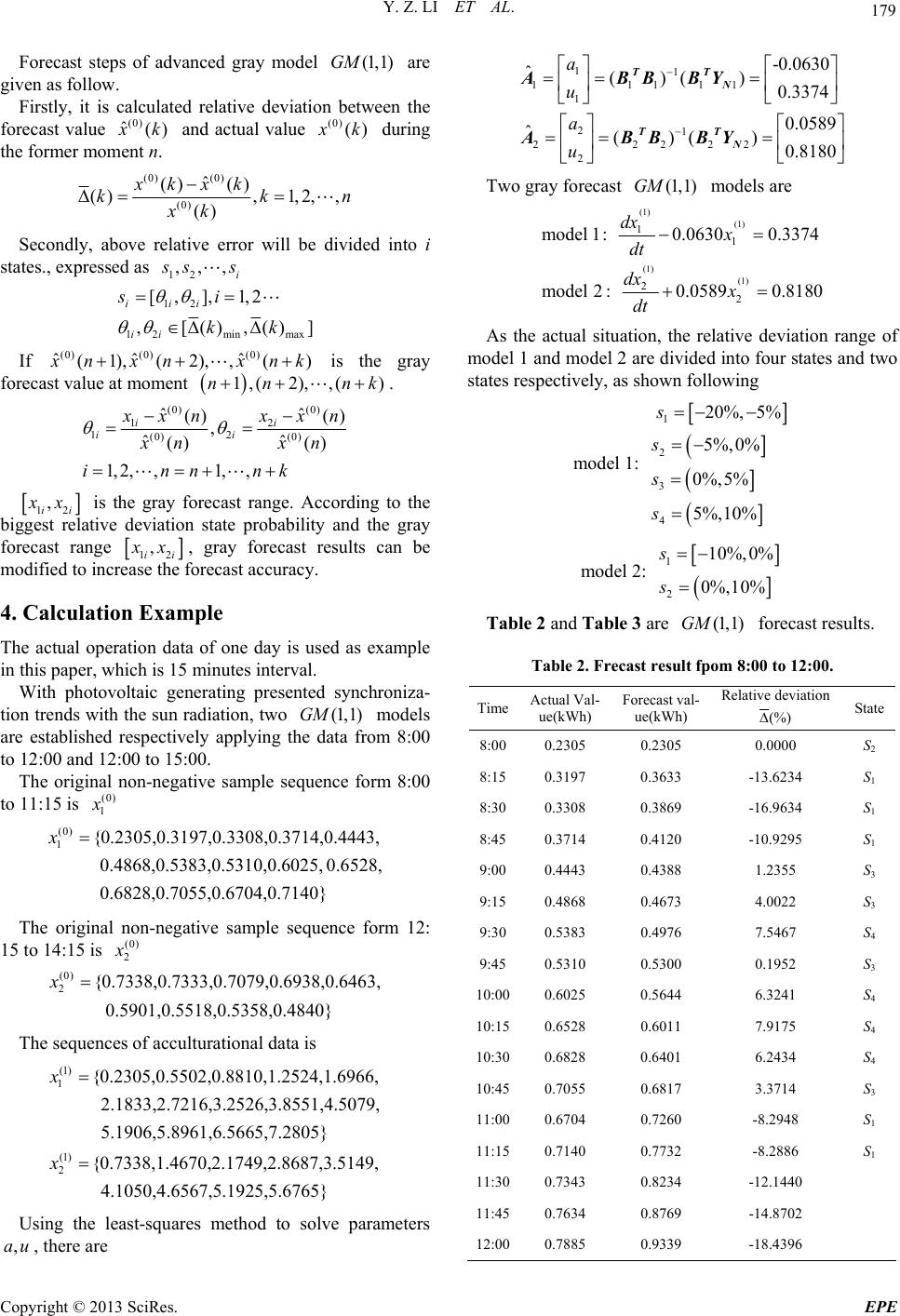 Y. Z. LI ET AL. 179 Forecast steps of advanced gray model are given as follow. (1,1)GM Firstly, it is calculated relative deviation between the forecast value (0) ˆ() x k and actual value (0)() x k during the former moment n. (0) (0) (0) ˆ () () (),1,2, , () xkxk kk xk n Secondly, above relative error will be divided into i states., expressed as 12 ,,, i s ss 12 12min max [, ],1,2 ,[(),() iii ii si kk] If (0) (0)(0) ˆˆˆ (1),(2), ,() x nxn xnk 1,( 2),nn k is the gray forecast value at moment ,( )n . (0) (0) 12 12 (0) (0) ˆˆ () () , ˆˆ () () 1, 2,,1,, ii ii x xnx xn xn xn innnk 12 , ii x x is the gray forecast range. According to the biggest relative deviation state probability and the gray forecast range 12 , ii x x, gray forecast results can be modified to increase the forecast accuracy. 4. Calculation Example The actual operation data of one day is used as example in this paper, which is 15 minutes interval. With photovoltaic generating presented synchroniza- tion trends with th e sun radiation, two models are established respectively applying the data from 8:00 to 12:00 and 12:00 to 15:00. (1,1)GM The original non-negative sample sequence form 8:00 to 11:15 is (0) 1 x (0) 1{0.2305,0.3197,0.3308,0.3714,0.4443, 0.4868,0.5383,0.5310,0.6025,0.6528, 0.6828,0.7055,0.6704,0.7140} x The original non-negative sample sequence form 12: 15 to 14:15 is (0) 2 x (0) 2{0.7338,0.7333,0.7079,0.6938,0.6463, 0.5901,0.5518,0.5358,0.4840} x The sequences of acculturational data is (1) 1 (1) 2 {0.2305,0.5502,0.8810,1.2524,1.6966, 2.1833,2.7216,3.2526,3.8551,4.5079, 5.1906,5.8961,6.5665,7.2805} {0.7338,1.4670,2.1749,2.8687,3.5149, 4.1050,4.6567,5.1925 x x ,5.6765} Using the least-squares method to solve parameters , there are ,au 11 11111 1 21 22222 2 -0.0 630 ˆ()( ) 0.3374 0.0589 ˆ()( ) 0.8180 a u a u TT N TT N ABBBY ABBBY Two gray forecast models are (1,1)GM (1) (1) (1) (1) 11 22 model 1: 0.06300.33 74 model 2: 0.05890.8180 dx x dt dx x dt As the actual situation, the relative deviation range of model 1 and model 2 are divided into four states and two states respectively, as shown following model 1: 1 2 3 4 20%, 5% 5%,0% 0%,5% 5%,10% s s s s model 2: 1 2 10%,0% 0%,10% s s Table 2 and Table 3 are forecast results. (1,1)GM Table 2. Frecast result fpom 8:00 to 12:00. Time Actual Val- ue(kWh) Forecast val- ue(kWh) Relative deviation (%) State 8:000.2305 0.2305 0.0000 S2 8:15 0.3197 0.3633 -13.6234 S1 8:30 0.3308 0.3869 -16.9634 S1 8:45 0.3714 0.4120 -10.9295 S1 9:00 0.4443 0.4388 1.2355 S3 9:15 0.4868 0.4673 4.0022 S3 9:300.5383 0.4976 7.5467 S4 9:45 0.5310 0.5300 0.1952 S3 10:00 0.6025 0.5644 6.3241 S4 10:150.6528 0.6011 7.9175 S4 10:30 0.6828 0.6401 6.2434 S4 10:450.7055 0.6817 3.3714 S3 11:000.6704 0.7260 -8.2948 S1 11:150.7140 0.7732 -8.2886 S1 11:300.7343 0.8234 -12.1440 11:450.7634 0.8769 -14.8702 12:000.7885 0.9339 -18.4396 Copyright © 2013 SciRes. EPE  Y. Z. LI ET AL. 180 Table 3. Frecast result from 12:15 to 15:00. Time Actual Val- ue(kWh) Forecast val- ue(kWh) Relative deviation (%) State 12:15 0.7338 0.7338 0.0000 S1 12:30 0.7333 0.7524 -2.6160 S1 12:45 0.7079 0.7094 -0.2095 S1 13:00 0.6938 0.6688 3.5969 S2 13:15 0.6463 0.6305 2.4321 S2 13:30 0.5901 0.5945 -0.7385 S1 13:45 0.5518 0.5604 -1.5763 S1 14:00 0.5358 0.5284 1.3752 S2 14:15 0.4840 0.4982 -2.9239 S1 14:30 0.4460 0.4697 -5.3029 14:45 0.4186 0.4428 -5.7766 15:00 0.3914 0.4174 -6.6551 Figure 1 is forecast results. (1,1)GM According to the verification model, the average of the original sequence is (0) 32 (0) (0) 11 2 10.7343 0.76340.78850.7621 3 10.8234 0.73430.0891 20.8769 0.76340.1135 30.9339 0.78850.1454 10.0891 0.11350.14540.1160 3 1() 3 0.7343 0.76210.7634 0.7621 1 30.7 k x sxkx 2 2 32 21 2 2 2 1 785 0.7621 0.0153 1 3 0.0891 0.11600.11350.1160 1 =30.1454 0.1160 0.0231 0.0231/ 0.01531.5098 k sk s cs 2 Probability of small error is 10.0891 0.1160 0.02690.67450.01530.0103 Figure 1. GM(1,1) forecast results. So the error can be concluded that the model does not meet the requirements, that is to say, the other method must be used in amend the gray model. Otherwise, the gray forecast model is correct. 5. Conclusions Photovoltaic (PV) power generation is a kind of green renewable energy. As distributed generation, it can not only complement energy to power system, but also en- hance the reliability of power supply. But the random- ness of photovoltaic power generation impa cts the stabil- ity of power system and the actual load demand directly. Therefore, the accurate forecast of power generation in grid-connected photovoltaic system is extremely impor- tant, and it will be useful to the planning and operation of whole system, so do well to load demand management. Operational characteristics of grid-connected PV sys- tems are coincided with gray theory application condi- tions. In accordance with the basic principles of gray theory, the greater of the data and the more comprehen- sive of information, the more accurate is forecast results. After leading into the verification model, the p robabil- ity of small error can suggest the accuracy of the gray forecast results. Once it exceeds the precision of allowed values, the gray forecast model must combin ed with oth- er advanced method, that is the combination model to ensure the forecast result, as in [8-11]. REFERENCES [1] J. H. Teng, T. S. Luor and Y. H. Liu, “Strategic Distrib- uted Generator Placements for Service Reliability Im- provements,” Power Engineering Society Summer Meet- ing, IEEE, Vol. 2, 2002, pp.719-724. Copyright © 2013 SciRes. EPE  Y. Z. LI ET AL. Copyright © 2013 SciRes. EPE 181 [2] R. E. Brown, J. P. Pan, X. M. Feng and K. Koutlev, “Sit- ing Distributed Generation to Defer T&D Expansion,” Transmission and Distribution Conference and Exposi- tion, Vol. 2, 2001, pp. 622-627. [3] Y. Li, “Research on the Parameters Theory and Applica- tion of the Linear Regression Model Based on the Gray System,” Application of Statistics and Management, Vol. 31, No. 3, pp. 440-446. [4] Y. J. Liu, Z. H. Li, F. SU and Y. C. Li, “Research on the Sensitivity of Outburst Predictors Based on Grey Rela- tional Analysis,” China Mining Magazine, Vol. 21, No. 9, pp.115-117. [5] D. X. Niu and J. R. Jia, “Application of Improved GM (1,1) Model in Load Forecasting,” Power Science and Engineering, Vol. 24, No. 4, pp. 28-30. [6] G. Mu, P. W. Guo, B. Xiao, Q. L. Liu, S. H. Yang, C. Zhou and Y. Zhang, “A Power System Monthly Load Forecasting Method Based on the Model of Grey-mean Generating Function,”. [7] Y. Y. Yu and Y. B. Yuan, “Forecasting Methods of Elec- tricity Qua ntity Based on Combined Model, ” Vol. 30, No. 2, pp.30-31. [8] Y. Z. Li, R. Luan and J. C. Niu, “Forecast of Power Gen- eration for Grid-connected Photovoltaic System Based on Grey Model and Markov Chain,” 3rd IEEE Conference on Industrial Electronics and Applications, Singapore, 2008, pp. 1729-1733. [9] W. Cui and M. Zhang, “Prediction of Load Based on Grey Theory and BP Networks,” Journal of Liaoning Technical University, Vol. 34, No. 4, pp. 631-633. [10] H. Y. Chen, X. D. Liu and C. Q. She, “Application of Improved Grey Theory to Short-term Load Forecasting,” International Journal Hydroelectric Energy, Vol. 29, No. 11, pp. 189-191. [11] Q. Huang and T. Ding, “Research on Power Economic Dispatch Based on Model of Combination Forecasting of Power Load,” Journal of Hubei University of Technology, Vol. 5, 2009, pp. 39-42. |

