Communications and Network, 2013, 5, 661-665
http://dx.doi.org/10.4236/cn.2013.53B2118 Published Online September 2013 (http://www.scirp.org/journal/cn)
Estimation of Non-WSSUS Channel for OFDM Systems in
High Speed Railway Environment Using Compr essive
Sensing*
Chen Wang, Yong Fang, Zhi-Chao Sheng
School of Communication and Information Engineering, Shanghai University, Shanghai, China
Received July 2013
ABSTRACT
Non Wide Sense Stationary Uncorrelated Scattering (Non-WSSUS) is one of characteristics for high-speed railway
wireless channels. In this paper, estimation of Non-WSSUS Channel for OFDM Systems is considered by using Com-
pressive Sensing (CS) method. Given sufficiently wide transmission bandwidth, wireless channels encountered here
tend to exhibit a sparse multipath s tructure. Then a sparse Non-WSSUS channel estimation approach is proposed based
on the delay-Doppler-spread function representation of the channel. This approach includes two steps. First, the de-
lay-Doppler-spread function is estimated by the Compressive Sensing (CS) method utilizing the delay-Doppler basis.
Then, the channel is tracked by a reduced order Kalman filter in the sparse delay-Doppler domain, and then estimated
sequentially. Simulation results under LTE-R standard demonstrate that the proposed algorithm significantly improves
the performance of channel estimation, comparing with the conventional Least Square (LS) and regular CS methods.
Keywords: OFDM; Non-WSSUS Channel Estimation; Compressive Sensing (CS); Kalman Filter; LTE-R
1. Introduction
In recent several years, High-Speed Railway (HSR) in
China has made great progress and attracted the world’s
attention [1]. The new speed record of high speed train is
at 486.1 km/h [2]. The broadband wireless access on
HSRs, also known as train-ground communication has
become a hot issue. To develop high quality service wire-
less communications that meet the demand of next-gen-
eration broadband wireless access for high-speed railway
has become an urgent problem. It has been shown that
the communication quality of the existing wireless net-
work of HSR s is qu ite po or , wh ere a h igh rate of dr oppe d
calls and low data rate are observed [3]. LTE-R [4,5]
basing on OFDM is commonly considered as a promis-
ing candidate to provide high quality of service. Since
the serious time and frequency selective fading, which
affects the OFDM symbol at the physical layer greatly
impacts system OFDM performance, the estimation and
compensation of the channel variation for each OFDM
symbol is crucial [6].
In the wireless communication, one of the most prac-
tical assumptions about the wireless channel is that of
Wide Sense Statio nary Uncorrela ted Scatteri ng, (WSSUS).
Existing fast fading channel estimation methods most
generalized stationary uncorrelated scattering (WSSUS)
as a precondition [7], or satisfied some certain channel
statistical characteristics, e.g. Jakes’ channels [8]. How-
ever, this assumption is no longer valid when the tran-
sceivers operate in the high speed railway environment.
Because for the HSR channel, the transceiver encounters
different channel conditions and the train runs across the
scenarios so rapidly [3]. This condition provokes the mul-
tipath arrivals associated with surface scattering fluctuate
rapidly over time, in the sense that the channel gain, the
arrival time, and the Doppler shifts of each arrival all
change dynamically [9], as a result the channel is Non-
WSSUS. The study of statistical characteristics of Non-
WSSUS has drawn much attention of researchers [10,11].
But in order to perform OFDM channel estimation, the
channel impulse response (CIR) is needed to be esti-
mated.
Apart from the fact that HS R channel is Non-WSSUS,
it is also sparse. For one thing, numerous experimental
studies undertaken by various researchers in the recent
have shown that wireless ch annels assoc iated with a num-
ber of scattering environments tend to exhibit sparse struc-
tures at large bandwidths [12]. For another, compared
*
This work was su pported by the National Science Fou ndation of Ch
i-
na (61271213, 61132004, 60972056)
.

C. WANG ET AL.
662
with urban and indoor conditions, the specular LOS com-
ponent is much stronger. Thus, the channel is generally
lower density scattered [3], which enhances the sparse
structures of the HSR channel.
According to the characteristics of HSR channel men-
tioned above, a Non-WSSUS channel estimatio n approach
is developed in this paper. It utilizes the channel delay-
Doppler-spread representation to accommodate the Non-
WSSUS of the CIR. This approach includes two steps. In
the first step, it utilizes the delay-Doppler shifts basis to
estimate the sparse HSR channel. In the second step, the
channel is tracked by a reduced order Kalman filter in the
sparse delay-Doppler shift domain, and then recovered
by CS method sequentially. One can, in turn, use the de-
tected pilots to perform a sequential approach for channel
estimation and data recovery. Our approach is not limited
by certain statistical characteristics.
This paper is organized as follows: Section 2 intro-
duces the Non-WSSUS channel and the OFDM system
models. Section 3 explains the estimation of the sparse
channel delay-Doppler-spread in the OFDM system. Sec-
tion 4 describes the sparse dynamic model for the Non-
WSSUS HSR channel, and then our proposed approach
for estimating Non-WSSUS channel is derived . Section 5
presents the simulations results which validate our ap-
proach. Finally, our conclusions are presented in Section
6.
2. Non-WSSUS Channel and OFDM System
Models
2.1. Non-WSSUS Channel Models
There are many equivalent ways of characterizing LTV
systems. We use the delay-Doppler-spread function C(υ,
τ) for channel characterization [13,14]. The time-varying
frequency response
H( ,)tf
and the delay-Doppler spread-
ing function constitute a two-dimensional Fourier trans-
form pair. It is defined by
22
2 H( ,)C(,)ee
j tjf
tf dd
πυ πτ
υτυ τ
−
=∫∫

(1)
The quantity
C( ,)dd υτυ τ
is the contribution to from
a scatterer at delay and Doppler. The discrete representa-
tion of Equation (1) is given by [12],
22
1
H( ,)ee
p
nn
Njf t
n
n
tf
πτ πυ
α
−
=
=
∑
(2)
which represents signal propagation over
p
N
paths. In
another word, there are
p
N
pairs, corresponding to dis-
tinct scatterers at different delay and Doppler. We as-
sume that the channel is maximally spread in the delay
and Doppler space,
max
[0, ]
n
ττ ∈
and
max
[0, ]
n
υυ ∈
. It
has been shown that if
n
α
(the discrete coefficients of
C( ,) υτ
) is a function of discrete time
n
: ()
n
n α
, then
channel is not WSS anymore [13]. If the matrix repre-
sentation of
n
α
is not diagonal, then channel is not US,
which wil l be furthe r de monst ra t e d in Sectio n 3.
2.2. OFDM System Models
In OFDM systems, the output symbol of the transmitter
at time
n
is given by the
N
point complex modulation
sequen ce
2
1
0
1
:e
j nk
NN
nk
k
xX
N
π
−
=
=∑
, where
k
X
is the
data symbol.
The orthogonal short-time Fourier (STF) basis wave-
forms
0
2
0
{ ()e)
jmW t
g tnT
π
−
, as a ge neralization of OFDM
signaling to counteract the time selectivity of doubly-
selective channels are used [14]. The parameter
0 maxmax
[ ,1/]T τυ ∈
and
0 maxmax
[ ,1/]W υτ ∈
correspond
to the time and frequency separation of the STF basis,
and are chosen so that
00
1TW =
(which gives rise to an
orthogona l STF basis).
3. Estimation of the OFDM Sparse Channel
Delay-Doppler-Spre a d
3.1. Delay-Doppler-Spread Representation
Consider signaling over wireless channels using symbols
of duration T and (two-sided) bandwidth W,
() 0xt =
[0, ] tT ∀∉
and
() 0Xf=
,
[/2, /2]f WW∀ ∉−
, the-
reby giving rise to a temporal signal space of dimension
0
N TW=
[12].
So the maximum number of resolvable delays,
max
1LW τ = +


and the maximum number of resolvable
Doppler shift,
max
/2 KT υ =

. The matrix representa-
tion of delay-Doppler-spread
n
α
[15] is as
0,0, 10,
1,1, 11,
1,1, 11,
H
KK K
KK K
LK LKLK
hh h
hh h
hh h
α
− −+
− −+
−−−− +−



=




 

(3)
Now recall from Section 2 that the time-varying fre-
quency response (Equation (2)). The virtual representa-
tion of a doubly-selective channel therefore implies that
2 2
1
0
H( ,)ee
l kjf
jt
LK W
T
l kK
tf
π π
α
−
−
= =−
≈∑∑
. Consequently, the
STF channel coefficients
,
{H }
nm
can be written as
2
2 1
, ,,
0
Heeu Hu
k
jn
Ntf
l
jm LK N
nmf mtn
lkK
π
π
α
α
− −
= =−
′
= =
∑∑
(4)
Where
00
//
tf
NTT NWW= =
0
0
2
0
e
jN
tf N
N NNW
π
−
= =
,
( 1)
u
1()0, ,1
tt t
tn
def knk nkn
NN Nt
t
WWW nN
N
− −+


== −



 

C. WANG ET AL.
663
1( 1)
,
1
u(1)0, ,1
ff
def m Lm
fmN Nf
t
W WmN
N
−


′== −



 
It is straightforward to see that if
H
α
is not diagonal,
then the
thl
scatterer will be interfer ed by other scatterers,
leading to a correlated scatterer.
3.2. Using CS to Estimate the Sparse Channel
Delay-Doppler-Spread
By sampling pilot symbols uniformly at random (without
replacement) from the whole temporal signal space of
dimension
0
N
, the D-sparse (the number of nonzero
elements of delay-Doppler-spread function is D) channel
delay-Doppler-spread estimation will have the following
equation,
HU vec(H)
pp t
w
α
= +
(5)
where
2
~ (0,)
t obs
wN I σ
,
()
H()
p
pp
yreceive pilots
x transmit pilots
=
,
,,
U{/(uu):(,)}
pptnf m
Nn mpilots ε
′′
= ⊗∈
,
ε
is the
system transmit energy budget, and
t
w
is the channel ob-
servation noise.
Since
H
α
is sparse, it is can be recovered form
H
p
by various CS methods (here we use OMP and CoSaMP).
Then the CIR can be built according to Equation (4).
4. Estimation of Non-WSSUS Channel
4.1. Non-WSSUS Channel Model
Since the HSR channel is determined by its delay-
Doppler-spread representation, we just need to discuss
the dynamic model for delay-Doppler-spread function.
For the currently non-zero coefficients of
H()n
α
at dis-
crete time n, we assume a spatially i.i.d. Gaussian ran-
dom walk model, with noise variance
sys
σ
. The initial
H (0)
α
is estimated by the CS sparse channel delay-
Doppler-spread estimation method mentioned in Section
3.
H (0)
α
is assumed to be generated from a zero mean
Gaussian with variance
2
D
σ
( )
2
1/
D
D σ =
, and the non-
zero element is randomly selected.
Let
T
n
denote the support set of
H()n
α
, i.e. the set
of its nonzero coordinates, and let
(H( ))
n
S sizen
α
=
. In
other words,
12
T [,]
n
nS
ii i=
where
k
i
are the non-zero
coordinates of
H()n
α
. Thus, under this assumption we
have the dynamic model shown in Table 1.
Table 1. Dynamic model for sparse delay-Doppler-spread.
H
α
(0) is generated from the D-sparse channel with randomly selected
nonzero elements
2
1
(H ())(H (1))(),() ~(0,),
ii ni nisysnn
nnvv NifiTiT
αα
σ
−
= −+∈∈
2
,1
(H ())(H (1))(),()~(0,),
ii ni niDnn
nnv v NifiTiT
αα
σ
−
= −+∈∉
(H ())(H (1))
ii
nnif i T
αα
=−∉
4.2. Estimation of Non-WSSUS Channel
Combining observation equation (Equation (5)) and state
equation (Table 1) together, we get Non-WSSUS chan-
nel representation by utilizing the sparse delay-Doppler-
spread function. This dynamic model of
H()
n
α
can be
tracked by Kalman filter, and then the CIR of Non-
WSSUS channel can be recovered, as a result, the Non-
WSSUS channel will be estimated sequentially. Since the
delay-Doppler-spread is sparse, KF-CS method is em-
ployed to solve the dynamic sparse channel problem. The
proof of the convergence of KF-CS and more details can
be found in [16,17]. Take the KF-CS algorithm into ac-
count, our proposed two-step approach is summarized in
Table 2.
5. Simulation
This approach was tested and compared according to the
LTE-R standard. The channel parameters are: Channel
parameters
max
:10 s
τµ =
, and the speed of the high speed
train is 500 km/h leading to
max 952.9Hz
υ =
with the
Carrier Frequency
2GHz
c
f=
. The system parameters
are: Total number of subcarriers N = 1024, number of
effective subcarriers are 600. The effective bandwidth is
W = 5.9 MHz. To avoid ISI, the symbol duration is 20
times of the
max
τ
, i.e.,
200μs
. The
0
1172N TW= =
and
(21) 180NL K=⋅+=
. For the OFDM system, the
STF basis parameters are chosen to be
0
90kHzW=
and
00
T 1/W=
to ensure an orthogonal STF, which corres-
pond to
18
t
N=
, Nf = 65. The pilot arrangements are
comb -type.
We first justify the first-step of the p ropose d appro ach.
The simulations are carried out under the assumption that
only 10% of the channel coefficients are nonzero, i.e. D
= 18. The channel matrix is generated from a zero mean
Gaussia n wi th varianc e
2
D
σ
.
Figure 1 depicts the mean square error (MSE) of the
channel estimates and the bit error rate (BER) versus the
channel signal-to-noise ratio (SNR) in the unit dB. It is
seen that both CS-based methods (with 10% pilots and
25% pilots) outperform the LS method (with 10% and
25% pilots) significantly. The LS and severely under-
performs the CS estimator with 10% pilots even when it
itself utilizes 25% pilots.
Table 2. Two step approach to estimate the HSR Non-
WSSUS channel .
1.
Utilize the delay-Doppler basis to e stimate the sparse delay-Doppler
-
spread function
Hα.
1.1.
Use the delay-Doppler basis Up and Hα
to rebuilt the estimated
CIR
.
2
. Run KF-CS algorithm to track the Hα(n)
in the sparse domain. Take
step
1.1 into account, the Non-WSSUS CIR can be estimated
sequentially
over time n.

C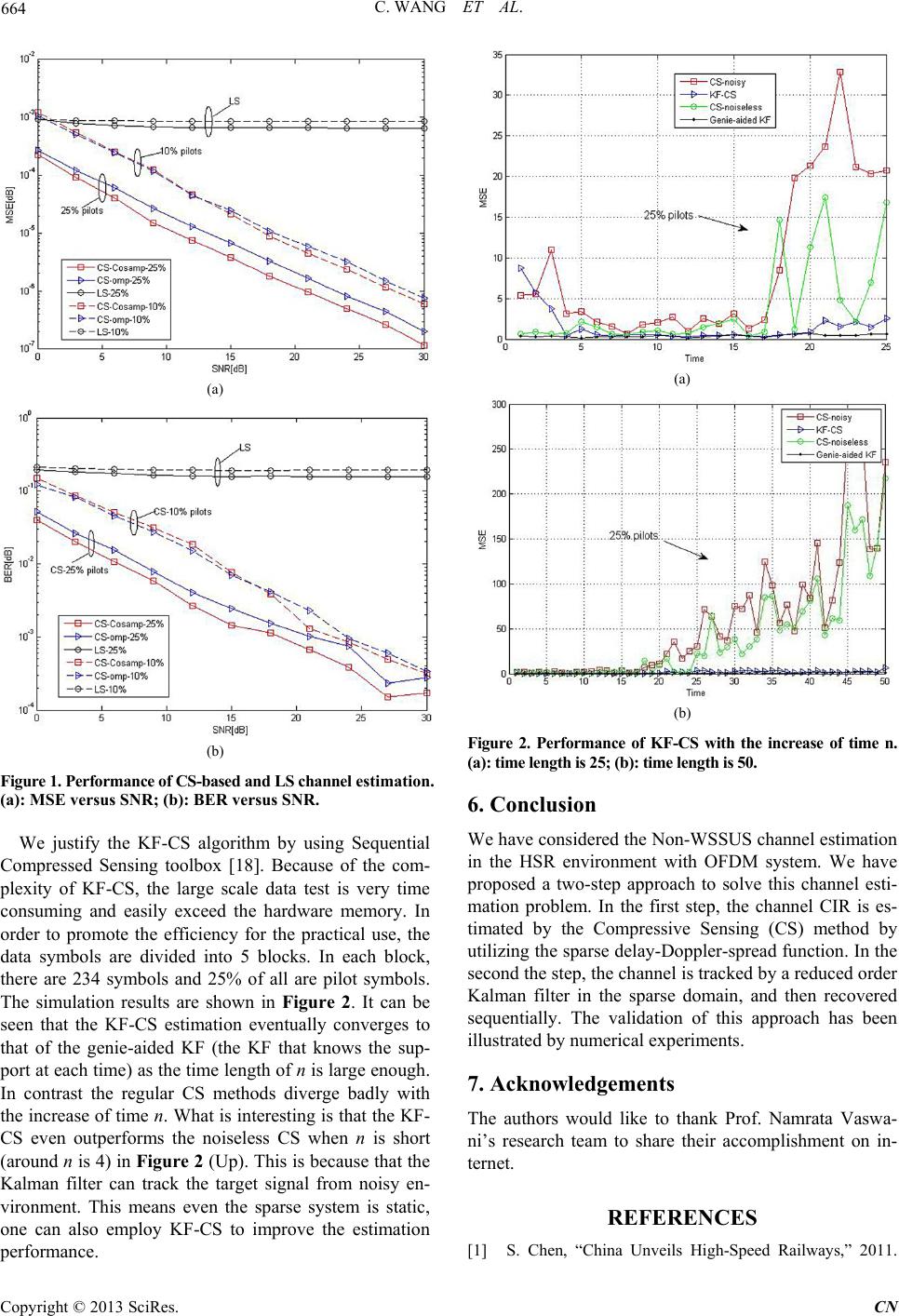. WANG ET AL.
664
(a)
(b)
Figure 1. Performance of CS-based and LS channel estimation.
(a): MSE versus SNR; (b): BER versus SNR.
We justify the KF-CS algorithm by using Sequential
Compressed Sensing toolbox [18]. Because of the com-
plexity of KF-CS, the large scale data test is very time
consuming and easily exceed the hardware memory. In
order to promote the efficiency for the practical use, the
data symbols are divided into 5 blocks. In each block,
there are 234 symbols and 25% of all are pilot symbols.
The simulation results are shown in Figure 2. It can be
seen that the KF-CS estimation eventually converges to
that of the genie-aided KF (the KF that knows the sup-
port at each time) as the time length of n is large enough.
In contrast the regular CS methods diverge badly with
the increase of time n. What is interesting is that the KF-
CS even outperforms the noiseless CS when n is short
(around n is 4) in Figure 2 (Up). This is because that the
Kalman filter can track the target signal from noisy en-
vironment. This means even the sparse system is static,
one can also employ KF-CS to improve the estimation
performance.
(a)
(b)
Figure 2. Performance of KF-CS with the increase of time n.
(a): time length is 25; (b): time length is 50.
6. Conclusion
We have considered the Non-WSSUS channel estimation
in the HSR environment with OFDM system. We have
proposed a two-step approach to solve this channel esti-
mation problem. In the first step, the channel CIR is es-
timated by the Compressive Sensing (CS) method by
utilizing the sparse delay-Doppler-spread function. In the
second the step, the channel is tracked by a reduced order
Kalman filter in the sparse domain, and then recovered
sequentially. The validation of this approach has been
illustrated by numerical expe riments.
7. Acknowledgements
The authors would like to thank Prof. Namrata Vaswa-
ni’s research team to share their accomplishment on in-
ternet.
REFERENCES
[1] S. Chen, “China Unveils High-Speed Railway s, ” 2011.

C. WANG ET AL.
665
http://news.bbc.co.uk/2/hi/8246600.stm
[2] D. Xin., “Record-Breaking Train on Track,” 2010.
http://www.chinadaily.com.cn/china/2010-12/04/content-
11651930.html
[3] L. Liu, et al., “Position-Based Modeling for Wireless
Channel on High-Speed Railway under a Viaduct at 2.35
GHz,” IEEE Journal on Selected Areas in Communica-
tions, Vol. 30, No. 4, 2012, pp. 834-845.
http://dx.doi.org/10.1109/JSAC.2012.120516
[4] T. Gao and B. Sun, “A High-Speed Railway Mobile
Communication System Based on LTE,” Electronics and
Information Engineering (ICEIE), 2010, Vol. 1, pp. 414-
417.
[5] K. Guan, Z. Zhong and B. Ai, “Assessment of LTE-R
Using High Speed Railway Channel Model,” Interna-
tional Conference Communications and Mobile Compu-
ting (CMC), 2011, pp. 461-464.
[6] F. Pena-Campos, et al., “Estimation of Fast Time-Vary-
ing Channels in OFDM Sy stems Using Two-Dimensional
Prolate,” IEEE Transactions on Wireless Communica-
tions, Vol. 12, No. 2, 2013, pp. 989-907.
[7] L. L. He, S. D. Ma, and Y. C. Wu, “Pilot-Aided IQ Im-
balance Compensation for OFDM Systems Operating
Over Doubly Selective Channels,” IEEE Trans on Signal
Processing, V o l. 59, No. 5, 2011, pp. 2223-2233.
http://dx.doi.org/10.1109/TSP.2011.2112649
[8] H. Hijazi, et al., “Channel Estimation for MIMO-OFDM
Systems in Fast Time-Varying Environments,” 2010 4th
International Symposium on Communications, Control
and Signal Processing (ISCCSP), 2010, pp. 1-6.
[9] W. C. Li, and C. P. James, “Estimation of Rapidly Time-
Varying Sparse Channels,” IEEE Journal of Oceanic En-
gineering, Vol. 32, No. 4, 2007, pp. 927-939.
http://dx.doi.org/10.1109/JOE.2007.906409
[10] G. Matz, “On Non-WSSUS Wireless Fading Channels,”
IEEE Transactions on Wireless Communications, Vol. 4,
No. 5, 2005, pp. 2465-2478.
http://dx.doi.org/10.1109/TWC.2005.853905
[11] M. Jachan and M. Gerald, “Nonstationary Vector AR
Modeling of Wireless Channels,” Workshop on Signal
Processing Advances in Wireless Communications, 2005,
pp. 625-629.
[12] W. U. Bajwa, et al., “Compressed Channel Sensing: A
New Approach to Estimating Sparse Multipath Channels,”
Proceedings of the IEEE, Vol. 98, No. 6, 2010, pp. 1058-
1076. http://dx.doi.org/10.1109/JPROC.2010.2042415
[13] T. H. Eggen, B. B. Arthur and C. P. James, “Communica-
tion over Doppler Spread Channels. Part I: Channel and
Receiver Presentation,” IEEE Journal of Oceanic Engi-
neering, Vol. 25, No. 1, 2000, pp. 62-71.
http://dx.doi.org/10.1109/48.820737
[14] Waheed Uz Zaman Bajwa, “New Information Processing
theory and Methods for Exploiting Sparsity Inwireless
SystemS,” Ph.D. Thesis, University Of Wisconsin-Ma-
dison, 2007.
[15] W. U. Bajwa, A. M. Sayeed and R. Nowak. “Learning
Sparse Doubly-Selective Channels,” 46th Annual Allerton
Conference on Communication, Control, and Computing,
2008, pp. 575-582.
[16] N. Vaswani, “Kalman Filtered Compressed Sensing,”
15th IEEE International Conference on Image Processing,
2008. ICIP 2008, 2008, pp. 893- 896.
[17] N. Vaswani, “Analyzing Least Squares and Kalman Fil-
tered Compressed Sensing,” IEEE International Confe-
rence on Acoustics, Speech and Signal Processing, 2009.
ICASSP, 2009, pp. 3013-3016.
[18] http://home.engineering.iastate.edu/~namrata/research/Se
quentialCS.htm